基于因子分析法的区域经济活力分析
2020-03-18田正浩
田正浩
(郑州大学 国际学院,河南 郑州 450000)
1 研究背景
经济活力是指在一定的发展时期内国家经济总供需的增长速度和发展潜力。在投资的角度来看,其主要包括国民生产总值的增长率(经济增长率)、固定投资率(资本积累率)和储蓄率及其变化等[1]。而城市经济活力与每个城市的经济发展能力以及潜力密切相关。目前我国城市的发展大部分都比较迅速,其城市经济活力主要表现在经济的成长及引进资本和吸引高素质劳动力的能力方面。近年来,为进一步提高经济活力,不少地区出台了有关刺激经济活力发展的优惠政策,如何对经济活力进行量化分析是当前需要解决的一大难题[2]。
2 模型的建立
2.1 经济活力影响因素关系模型
本文以亚太数学建模中城市相关数据为研究对象进行经济活力的衡量。企业存活数量是衡量区域经济活力的重要指标,而区域的常住人口数量与企业存活数量的相关系数R=0.703 6,存在较强的正相关关系(见图1和表1),则区域的常住人口数量也为影响经济活力的指标之一。从附件3中可知,不同区域的企业注册资本分布无明显差别,即企业的注册资本对经济活力影响较小,此指标的影响可以忽略不计。综上,区域的常住人口数量与企业存活数量均对经济活力造成一定的影响,在本文中,以此为基础,结合查询的资料推断出可能存在的影响因素指标。
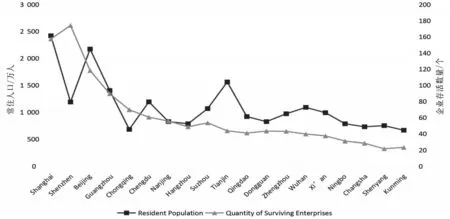
图1 常住人口和企业存活数量变化折线

表1 相关系数
由对经济活力的定义可知,经济活力主要表现在经济成长的能力,引进资本和吸引高素质劳动力的能力[3]。因此从城市的经济成长能力出发,可能的影响因素有:人均GDP、国内生产总值增长率、进出口额、第三产业增加值、企业存活个数;从城市的引进资本能力出发,可能的影响因素有:实际利用外资金额;从吸引高素质劳动力的能力出发,可能的影响因素有:城镇失业率、人均可支配收入、发明专利授权量,在职人员平均工资,常住人口数量。
2.2 经济活力影响因素关系模型
2.2.1 思路分析
接下来需要在经济活力影响因素关系模型建立的基础上选取合理的指标体系,用来评价上海、深圳等19个城市的经济活力。即构建一个评价体系,来判断某因素是否对城市经济活力存在影响,影响的程度有多大。思路分析如图2所示。2.2.2构建指标体系
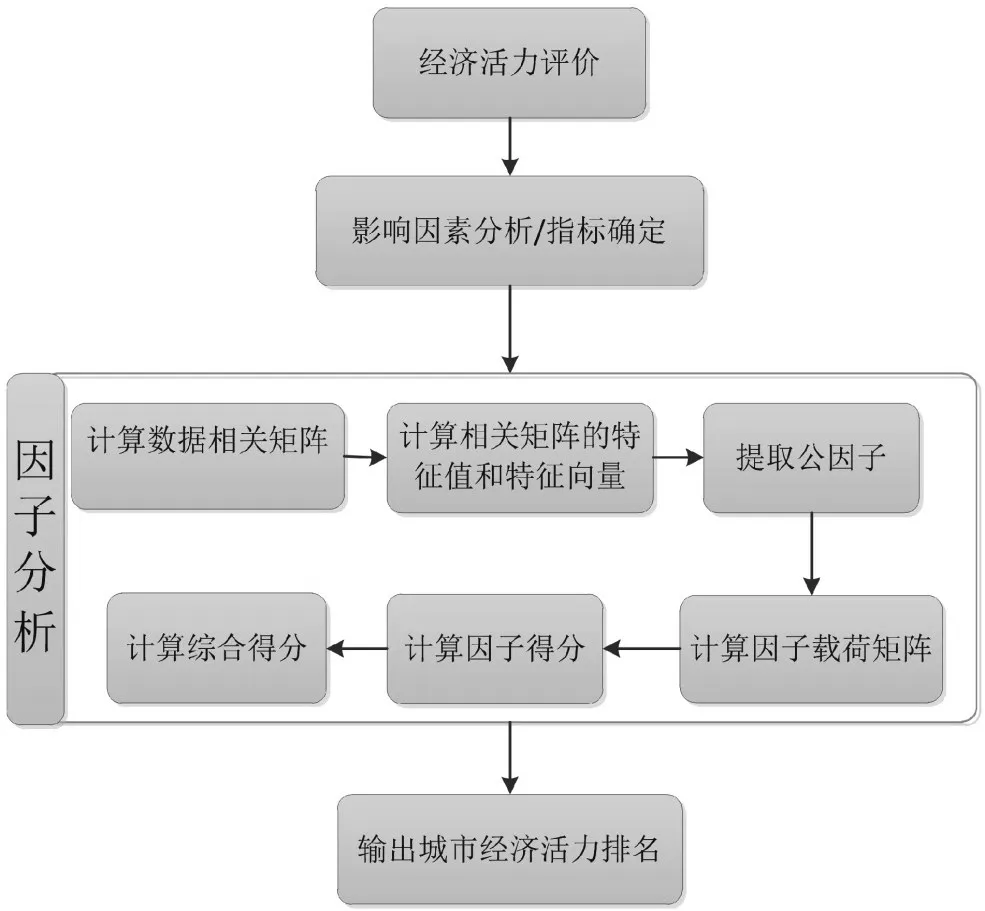
图2 求解思路分析
(1)评价指标选取原则。区域的经济活力影响因素很多,我们需要选取科学合理的指标来对其进行综合评价。在本文中,我们依照以下原则来选取科学合理的指标。
简单性原则:尽量选取简单、可量化和规范化的指标。
全面性原则:选取的指标要能基本涵盖所有影响经济活力的因素。
科学性原则:所选择的指标都是合理严谨的。
时效性原则:选取的指标在研究问题的相近时间段内对结论具有价值。
(2)评价指标的确定。按照上诉原则,在本文中选取了人均GDP,国内生产总值增长率,进口额占国内生产总值的比例,出口额占国内生产总值的比例,第三产业增加值,企业存活个数,实际利用外资金额,城镇失业率、人均可支配收入、发明专利授权量,在职人员平均工资,常住人口数量、企业注册个数以及R&D经费投入金额共14个指标用以从经济成长能力、引进资本能力和吸引高素质人才能力的角度来反映经济活力,指标的具体含义如表2所示。2.2.3综合评价模型的建立
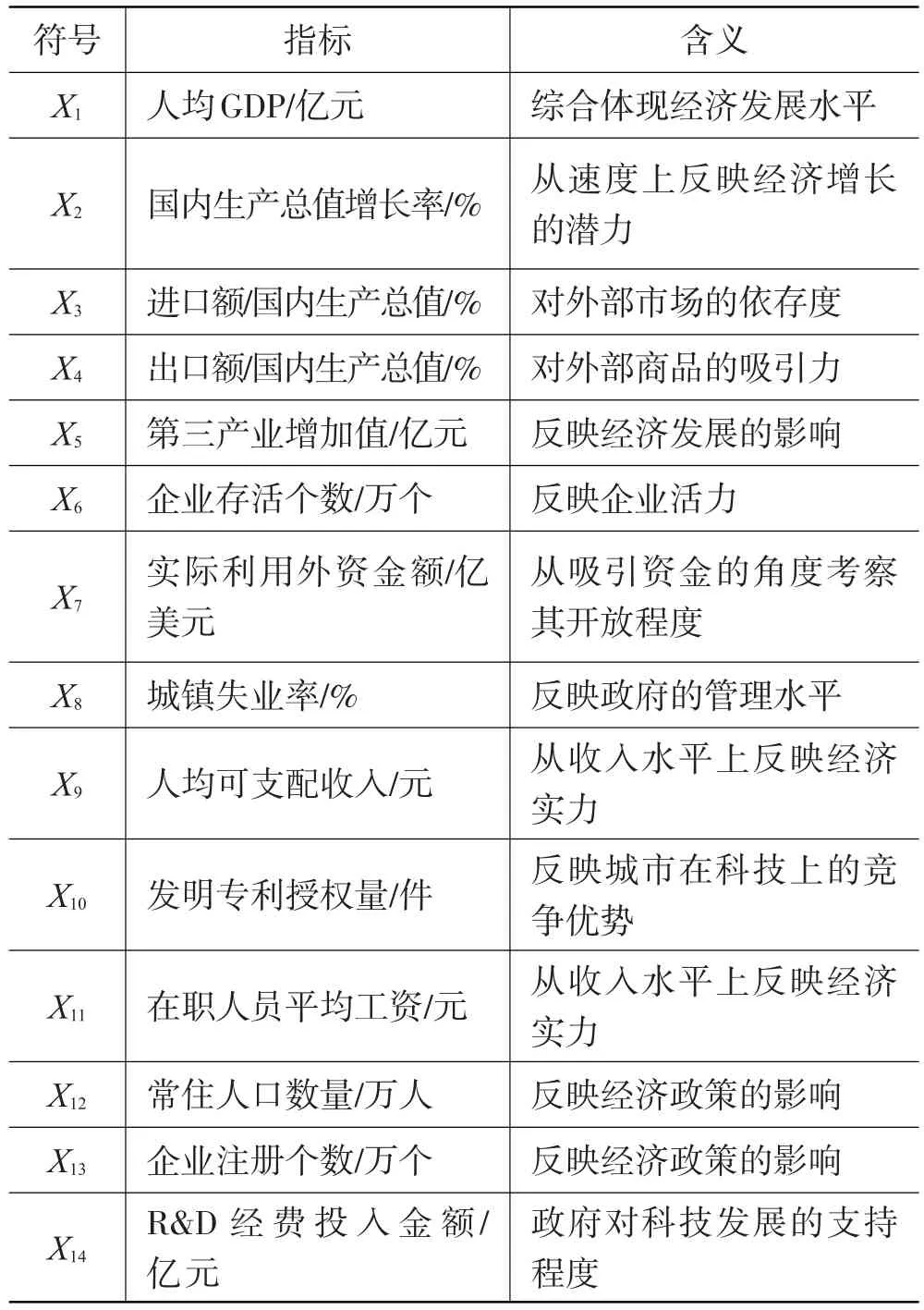
表2 指标体系及其含义
本文中,以因子分析法为算法基础建立了综合评价模型。在因子分析法中,要根据具体问题对观测变量分类,将相关性较高的变量分在同一类中,而不同类变量之间的相关性则较低,因此不同类变量实际上就代表了不同的基本结构,也就是公共因子。对于所研究的问题就是寻找用个数最少的公共因子的线性函数与特殊因子之和来描述原来观测的每一分量。因子分析法的数学表示为:X=AF+B。
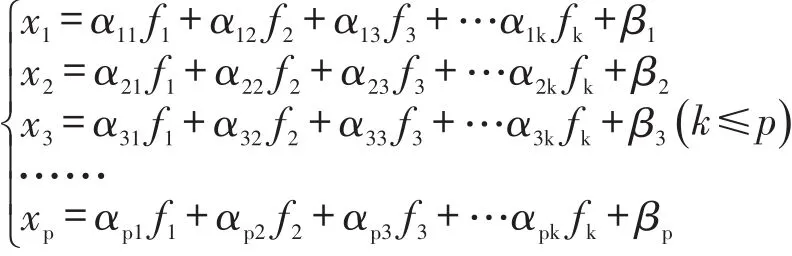
上式中,向量X(x1,x2,x3,…,xp)为原始观测变量。F(f1,f2,f3,…,fk)是X(x1,x2,x3,…,xp)的公共因子,这些因子在原观测变量的表达式中同时出现,它们之间无相关性。公共因子F(f1,f2,f3,…,fk)的系数A(aij)为因子载荷矩阵,代表了第i个变量在第j个公共因子上的权重。B(β1,β2,β3,…βp)为X(x1,x2,x3,…,xp)的特殊因子,各特殊因子之间包括特殊因子和公共因子之间均无相关性。
3 模型求解
3.1 数据获取
按照构建的指标体系,查询得到相应的数据集(数据来源:统计年鉴、统计公报、科技经费投入公报等),部分数据如表3所示。

表3 部分指标数据
3.2 模型求解
在进行因子分析综合评价前,由于不同指标的数据间存在量纲的影响,因此对采集到的原始数据进行归一化处理,消除量纲。对归一化后的数据运用SPSS统计分析软件进行分析,得到的结果如下所示。
从总方差解释表中(见表4)可以知道,在初始解中提取了4个综合因子,其方差总贡献率为86%,即可以描述原变量信息达到86%。
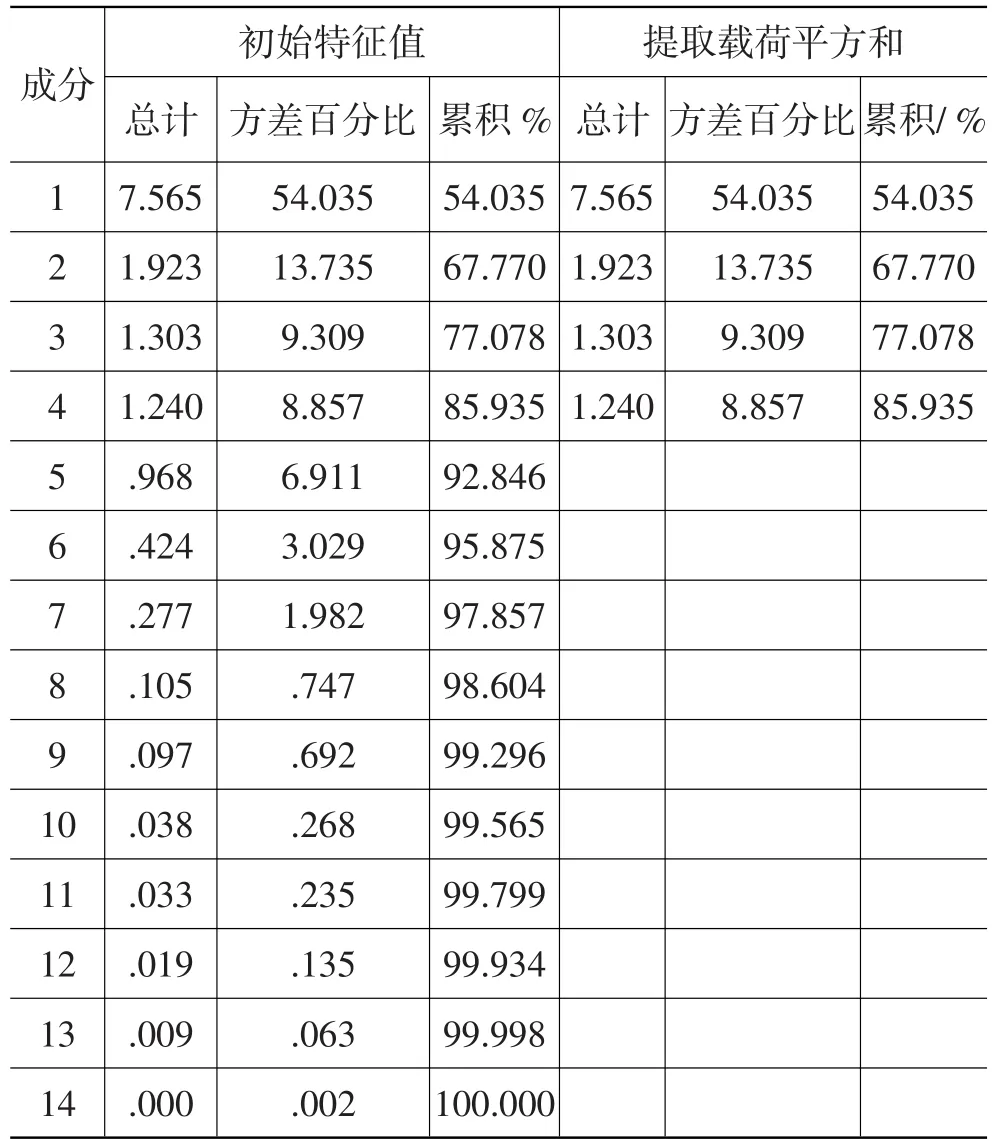
表4 总方差解释
由成分矩阵表(见表5)可知,4个主成分与原始变量之间的关系可以采用以下线性组合进行表示:

由于每个主因子只反映了各城市经济活力的单方面特征,因此本文采用各因子的方差贡献率作为权重来计算因子的总得分,加权求和,其数学模型如下:
F=0.54×F1+0.11×F2+0.09×F3+0.08×F4
计算得到各城市的总得分,按照降序排列,结果如表6所示。
可以知道,在此数据集下,2018年城市活力值最强的是武汉,其次是上海和北京,成都和深圳紧随其后。

表5 成分矩阵
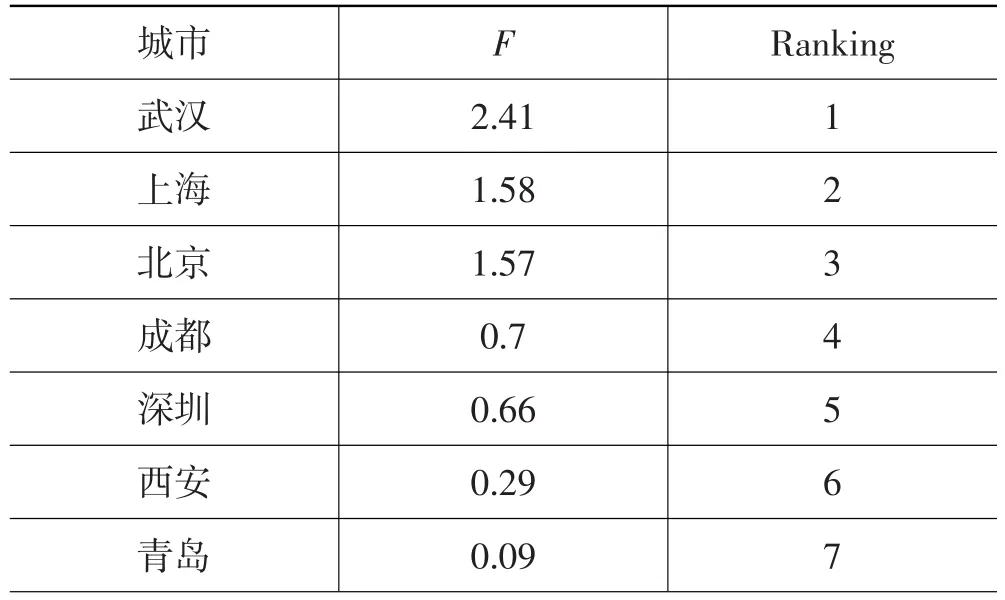
表6 城市活力排序

续表6
