基于条件生成式对抗神经网络的一维光学晶格中BEC动量分布研究

(西安工程大学电子信息学院 陕西 西安 710048)

一、引言

自2002年德国Munich研究小组通过控制光晶格[1]的阱深，实现了将超冷原子从超流态向Mott绝缘态的相变[2]。在传统的超冷原子研究计算中，对于一维光晶格中的玻色爱因斯坦凝聚体的波函数的计算，通常采用托马斯-费米近似和高斯近似模型求得[3,4]。通过波函数的叠加[5]再做傅里叶变换，最后得到在实验上观测到的动量分布。本文建立改进的条件生成对抗网络研究一维光晶格中稀薄气体玻色-爱因斯坦凝聚体的相位与出其动量分布。

二、条件生成式对抗网络

生成式对抗网络是Goodfellow在2014年提出的[6]，其原理基于博弈论的思想，通过将生成网络与判别网络作为两位博弈方，即一方获得，另一方就会有损失。通过双方不断地博弈最终达到一种平衡。其模型如图1所示：

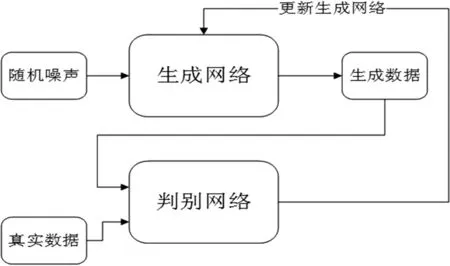
图1 生成式对抗网络模型

其数学表达式如公式1所示：

(1)

D表示判别网络，G表示生成网络，z表示随机噪声。其含义就是判别网络最大化分辨真实数据与生成数据，而生成网络则是要不断减小生成数据与真实数据的差距。相较于其他神经网络模型，生成判别网络可以生成更好的结果，但是由于生成网络的输入来自随机噪声，这样会导致生成网络的训练过于缓慢，所以在Mirza提出在通过加入一个条件变量来约束输入噪声，于是就有了条件生成对抗网络[7]，其数学表达式如下

(2)

y表示为条件变量用来约束随机噪声z，我们对条件生成对抗网络的内部结构进行了设计，生成网络我们采用3层卷积层[8]和2层循环层[9]组成，判别网络用3层卷积层以及两层的全连接层组成，其结构如图2所示：

图2 条件生成式对抗网络

三、实验细节与结果分析

(一)实验数据集及网络模型参数

实验中，我们通过托马斯费米理论进行计算得到波函数的两个特征，即相位信息与原子密度信息，生成106组值作为一维光晶格中106个格点的波函数特征，其每组数据维度为106*2，我们生成了5000组数据作为实验数据，其中将4500组作为训练数据集，250组作为验证数据集，250组作为测试数据集。条件生成对抗网络的超参数如表1所示：

表1 生成网络的超参数

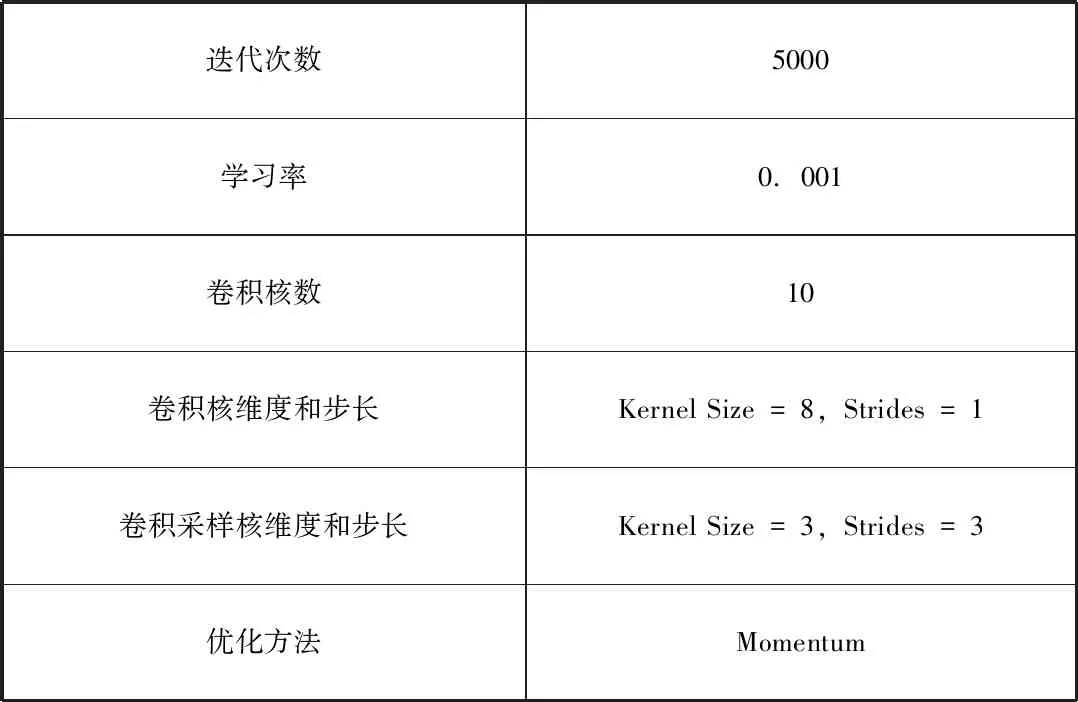
表2 判别网络的超参数

循环网络层选用Relu[10]作为激活函数，卷积层选用的激活函数选用LeakyRelu[11]，LeakyRelu可以保留卷积层输出的负值相位特征，其表达式为：

y=max(0.2x,x)

(3)

(二)实验结果

我们用平均误差来评估模型的效果，网络模型不能根据测试数据集的结果进行调整且测试数据集绝对未知，所以测试集的结果可以作为最终的评估结果，其结果如表2所示。图3是在训练过程中，卷积循环网络模型在验证数据集上的平均误差，图4是训练完成后，卷积循环神经网络在测试数据集上的结果。

表3验证集和预测集下的神经网络的平均误差

Table3.AverageErrorofNeuralNetworksbasedonVerificationSetandPredictionSet

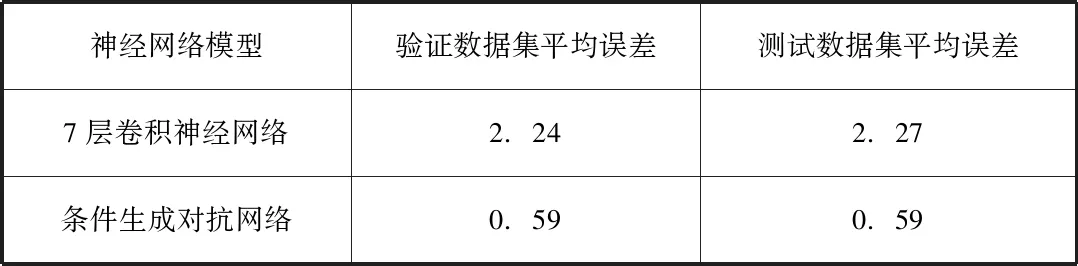
神经网络模型验证数据集平均误差测试数据集平均误差7层卷积神经网络2.242.27条件生成对抗网络0.590.59

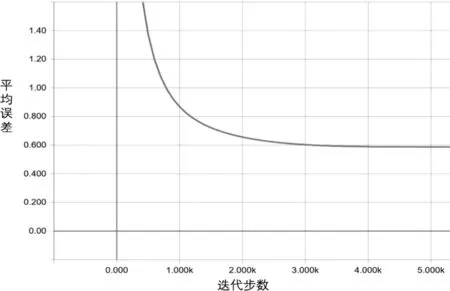
图3 生成网络在验证数据集上的平均误差

图4 网络模型在测试数据集上的结果

(三)实验结果分析

通过表3可以看出，条件生成对抗网络模型的效果不管是在测试集上，还是验证测试集上平均误差都有明显的下降，其误差结果为0.59，相较于7层卷积神经网络，误差降低了74%。通过图4可以看出训练完成的模型能比较明显的预测出一维光晶格中的超冷凝聚体在动量空间中的几个峰值以及位置。

四、结论与展望

本文从数据科学的研究角度出发，将机器学习的方法，运用到冷原子物理中，建立卷积循环网络模型，通过一维光晶格中的玻色-爱因斯坦凝聚体的波函数预测其动量空间的分布，不仅对基础研究有开拓性的意义，甚至是对高精密测量，量子信息处理方面都有积极的意义。