变式教学:从面积法到体积法

(重庆三峡学院，智能信息处理与控制重庆高校市级重点实验室 重庆 万州 404100；重庆三峡学院，物联网与智能控制技术重庆市工程研究中心 重庆 万州 404100)

一、前言

华人的数学学习给人的印象是，缺乏主动性，主要靠记忆、模仿和刻意练习、题海战术。然而，在国际数学教育测试PISA中，华人地区的学生的数学成绩却十分优异。这个现象被称为“中国学习者悖论”。国际研究者总结华人地区数学教育的优势时，提出了变式教学理论。1981年，顾泠沅系统综合了变式教学的概念，形成了概念性变式和过程性变式的变式教学理论。以面积法和体积法为研究对象，从过程性变式的角度来解释，两种方法的变式教学过程以及学习心理优势，希望得到一定的借鉴和交流，促进教学改革水平的提升。

二、过程性变式

过程性变式是在数学教学活动中，按照层次有序推进。我们知道，数学教学活动中有两种知识，一种是陈述性知识(概念)，还有一种是程序性知识(过程)。由于程序性知识是动态的，涉及到学习问题解决和元认知策略，掌握起来比较困难。然而，数学活动过程一般是具有层次性的，它包含为解决问题而采用的一系列不同步骤和策略，采用过程性变式，可以促进概念的形成、问题解决的铺垫、构建数学经验体系[1]。

三、面积法

面积法这个概念是需要通过一系列的过程促进发展形成的，教师可以从过程性变式来建立面积法的概念。

原 题

已知等腰三角形ΔABC的高AD,从点D分别作DE⊥AB于E,DF⊥AC于F,求证：DE=DF。

解法分析

用三角形全等也可以证明，假如能够发现等腰的高分等腰三角形为两个面积相等的直角三角形。DE,DF分别是这两个直角三角形斜边上的高，根据面积法，可证明。

DE=DF。

变式1

已知等边三角形ΔABC内有一点P,从P点分别向AB,BC,CA作垂线，垂足分别为D,E,F,求证：PD+PE+PF为定值。

解题分析

h1+h2+h3=h(定值)

理论层面，现有研究对国际舆论态势的基本判断仍是“英语霸权”“西强东弱”。国际传播的信息流亦呈现从西向东、由北到南、从发达国家流向发展中国家的状态。[11]在“一带一路”背景下，在国际舆论的话语实践中，中国需要调整以往在国际传播中的边缘心态，增强主动传播的意识，从被动的对媒介帝国主义的抵抗，转向积极地具有传播主体意识的议题建构，[12]从而形成“融通中外的话语体系”。培养合作传播思维，通过媒介合作共同打造话语空间，与周边国家和发展中国家构建话语共同体。未来的国际传播格局同样需要合作、融合、共赢的思维。相应地，未来的研究应关注如何通过媒介合作提高我国在国际传播中的主体地位问题。

变式2

已知等边三角形ΔABC，边长为a，求内切圆的半径r。

解题分析

变式3

已知直角ΔABC的两个直角边长为a,b,求它的内切圆的半径。

解题分析

四、体积法

已知四面体S-ABC,SA=SB=SC,底面ΔABC为等边三角形，求证：ΔABC的中心O到三个侧面的距离相等。

解题分析

从体积法的角度理解，可以发现这个四面体的对称性,可以做辅助线，将四面体分解为三个体积相等的四面体，即可证明结论。

变式1

已知正四面体S-ABC，各边长分别为a，内部有一点P,到每个面的距离分别为h1,h2,h3,h4，求证：h1+h2+h3+h4为定值。

解题分析

h1+h2+h3+h4=h(定值)

变式2

已知四面体S-ABC，SA，SB，SC两两相互垂直且长度相等为a，求顶点S到底面三角形ABC的距离。

解题分析

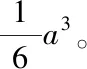
变式3

已知四面体S-ABC，SA，SB，SC两两相互垂直且长度相等为a，求这个四面体的内切球的半径。

解题分析

五、教后反思：变式教学的解释

教师实施变式教学，设计过程性变式。从一系列变式1,2,3，可以让学生理解到数学问题解决的一个基本思路，把没有解决的问题转化为已经解决的问题，逐步化规设置路径。设计过程性变式的目的是增加活动的多样性以及活动的层次性。这些变式就形成了一个划归或探索的步骤和策略，这与教学策略中的“脚手架理论”不谋而合，这些变式就形成了学习者的一个经验策略系统，成为学习心理优势的一个重要部分[1]。虽然没有定义面积法、体积法，过程性变式的教学策略使得学生产生了有意义的学习，帮助学生建立了知识之间的联系，促进了学生的身心和能力的发展[1]。教师作为一个反思型实践者，可以在日常的教学去设计变式教学的案例，促进学生数学学习[2，3]。