山火中颗粒物对直流导线表面电场影响仿真研究

刘 程, 孔祥美

(广东电网有限责任公司汕头供电局，广东 汕头 515000)

0 引 言

随着中国特高压输电线路的大力建设，导线产生的电磁环境问题得到了更广泛的关注[1-3]。相对于特高压交流输电线路，特高压直流输电线路导线表面更容易聚集和吸附颗粒物[4]。直流导线电晕的产生以及电晕所引发的可听噪声、无线电干扰等问题与导线表面粗糙程度密切相关。目前对输电线路电磁环境研究中仅考虑清洁导线，针对空气中颗粒物对直流导线表面场强影响考虑不足。

近年来，随着清明祭祀、放火烧荒以及各种极端气象灾害的增多，导致输电线路走廊山林火灾事故急剧攀升[5-6]。山林火灾燃烧后期产生的烟尘等颗粒物，会附着在直流导线表面，严重威胁着特高压直流输电线路的安全运行。因此，研究山林火灾燃烧后期空气中颗粒物对直流导线表面电场的影响具有重要意义。

植被燃烧产生的烟尘在热浮力的作用下向导线运动，在直流线路电磁场的作用下吸附在导线表面，导致线路表面电场强度急剧增加，对输电线路电磁环境产生重要影响[7-11]。因此，此文采用Ansoft有限元软件仿真研究了空气中颗粒物形状及种类对导线表面场强的影响，对于直流输电线路的设计和运行维护具有重要的指导意义。

1 电场分析理论基础

1.1 电场分析数学模型

电场仿真理论基础是麦克斯韦方程组的微分形式，特高压直流导线为严格的轴对称结构，其求解可归结为二维轴对称静电场边值问题，利用麦克斯韦方程组的微分形式描述准静态场中的电场方程[12-14]：

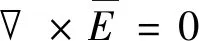
(1)

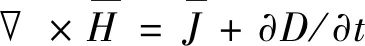
(2)

(3)

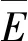
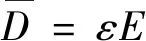
(4)

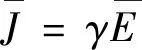
(5)

式中：ε为相对介电常数(F/m)；γ为电导率(S/m3)。当介质电导率γ和相对介电常数ε都是常数时，介质为线性介质。由式(1)～(5)可以看出，介质中同时存在自由电荷引起的传导电流和位移电流，电场分布由介质介电常数和电阻率同时决定。

在直流电压下，特高压直流导线为电流传导场，介质内部场强分布只与电阻率有关。而静电场场域中电位与电场关系为

(6)

式中：φ为整个场域中的电网函数。

由上述各式得到了电准静态场中的电位方程描述为

(7)

同时考虑了传导电流和电介质对场域中电位分布的影响，可用于求解任何场源激励下电介质中的线性电场电位分布。

1.2 电场计算的边界条件

电磁场理论中，电场具有三类边界条件[15-16]，此文采用第一类边界条件(Dirichlet边界条件)，即已知边界上的电位值：

φ|Γ1=φ(t)

(8)

第二类边界条件在有限元计算时自动满足变分条件，又称自动边界条件；第一类边界条件需要手动指定，又称为强加边界条件。实际计算时，只需定义第一类边界即可，第三类边界条件为混合边界条件，即第一类边界与第二类边界的线性组合。在高压导线中，不存在第三类边界条件。

2 建立仿真模型

空气中颗粒物形状和尺寸具有多样性，因而会在导线表面形成形态各异的凸起。同时，空气中不同种类颗粒物也会对导线表面电场强度产生重要影响。

此文采用Ansoft有限元分析软件，仿真研究不同形状以及不同种类颗粒物对导线表面电场强度的影响。为了简化仿真，建立二维模型进行仿真分析，仿真几何模型如图1所示[17]。几何模型中导线采用半径R=10 mm的光滑导线，用来仿真分析无颗粒物时导线周围场强，钢芯铝绞线电导率为σ=323 800 S/m，求解域材料属性设置为空气。

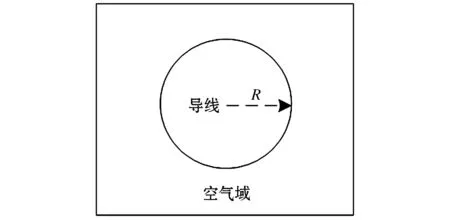
图1 光滑导线仿真模型Fig.1 Simulation model of smooth conductor

由于空气中颗粒形状差异较大，为了简化仿真，研究颗粒物几何形状对导线表面场强的影响时，颗粒物形状主要考虑椭圆形、圆形、菱形3种情况，颗粒物几何模型如图2所示。颗粒物种类主要为木炭颗粒(电导率为18 518.5 S/m，相对介电常数为1.8)以及地面硅藻土颗粒(电导率为0 S/m，相对介电常数为4)。此文以导线起晕场强E=18 kV/cm作为标准值，通过采用不同几何形状、不同种类颗粒物顶部场强与标准值之比表征颗粒物对导线表面电场的畸变程度。

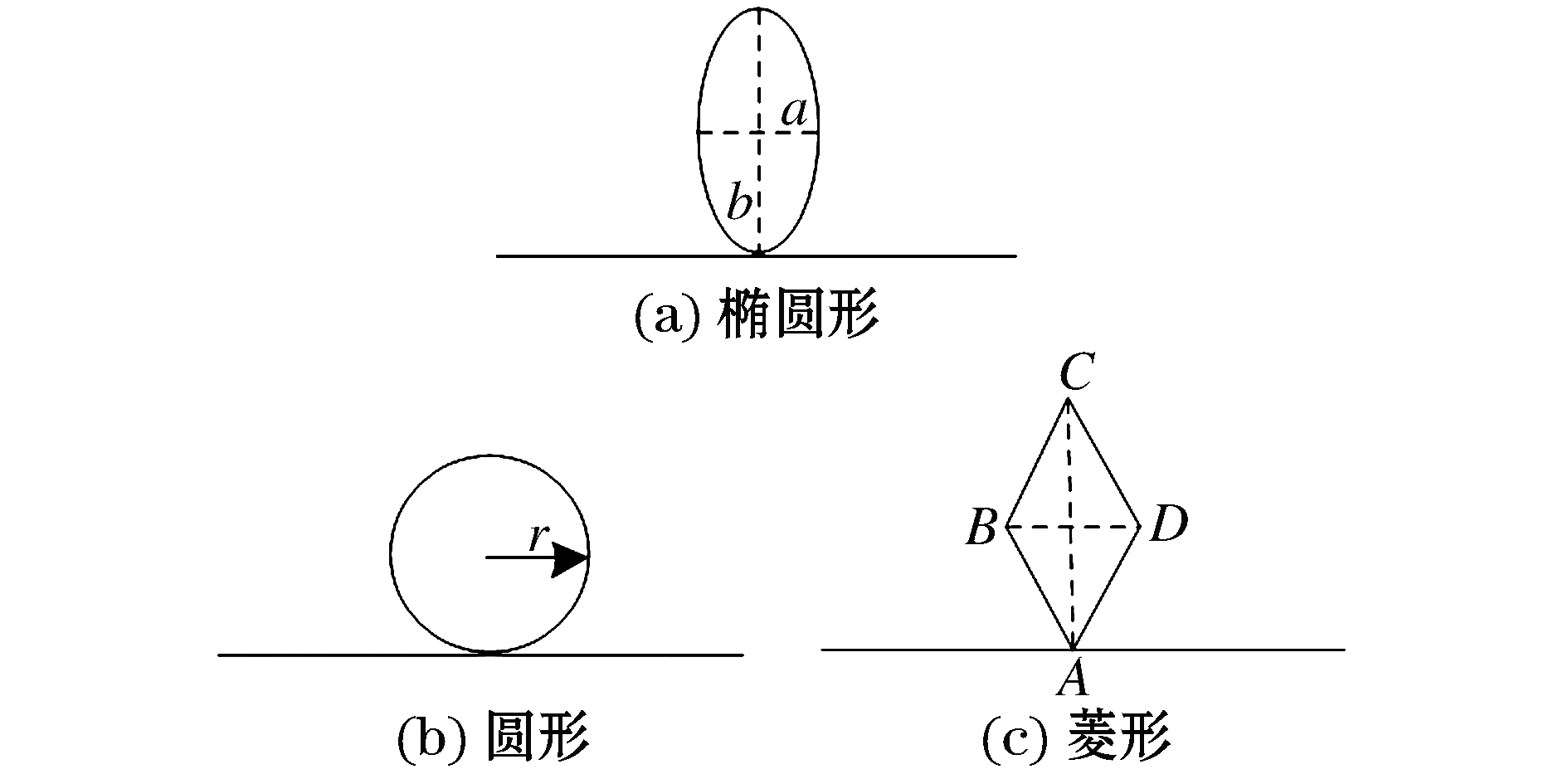
图2 颗粒物仿真模型Fig.2 Simulation model of Particles

3 边界条件确定及有限元网格划分

3.1 边界条件确定

电场分析的区域为无限空间，在仿真模型建立时，将电场的无限场域简化为有限场域，即采用一条假想的边界，用Ansoft远场边界来近似等效无限远空间，在假想的边界上电压及电场均为0，边界等效的处理对精确的电场分析起到关键作用。

3.2 有限元网格划分

为了提高计算速度，节省计算时间，网格划分采用三角形单元划分法[18]。为使计算误差分布均衡，采用自适应有限元技术按电场强度、电位值或误差值大小指导场域的疏密剖分，采用该剖分方法可以有效地控制网格单元的大小和密度的分布，保证网格中的每个三角形单元都对电场计算结果提供几乎相同的精度。同时在靠近导线边缘位置处对所划分的网格进行再剖分，因此，靠近导线处网格划分得较为密集；而对于导线周围较远区域网格划分得相对稀疏，符合有限元法网格划分的基本原则。

4 仿真结果分析

4.1 椭圆形颗粒物

椭圆形颗粒的几何参数主要为颗粒短轴长度a和长轴长度b。椭圆形颗粒对电场的畸变云图如图3所示，由图3可以看出，椭圆形颗粒物对导线表面电场具有明显的畸变作用，越靠近椭圆形颗粒物尖端畸变效果越明显，同时颗粒物内部场强为零。当椭圆形木炭颗粒长轴长度恒定时，颗粒顶部场强随椭圆形颗粒物短轴长度的变化规律如图4所示(其中木炭颗粒长轴长度分别选择200 μm、400 μm、600 μm)。不同种类颗粒物顶部场强随椭圆形颗粒短轴长度变化规律如图5所示。

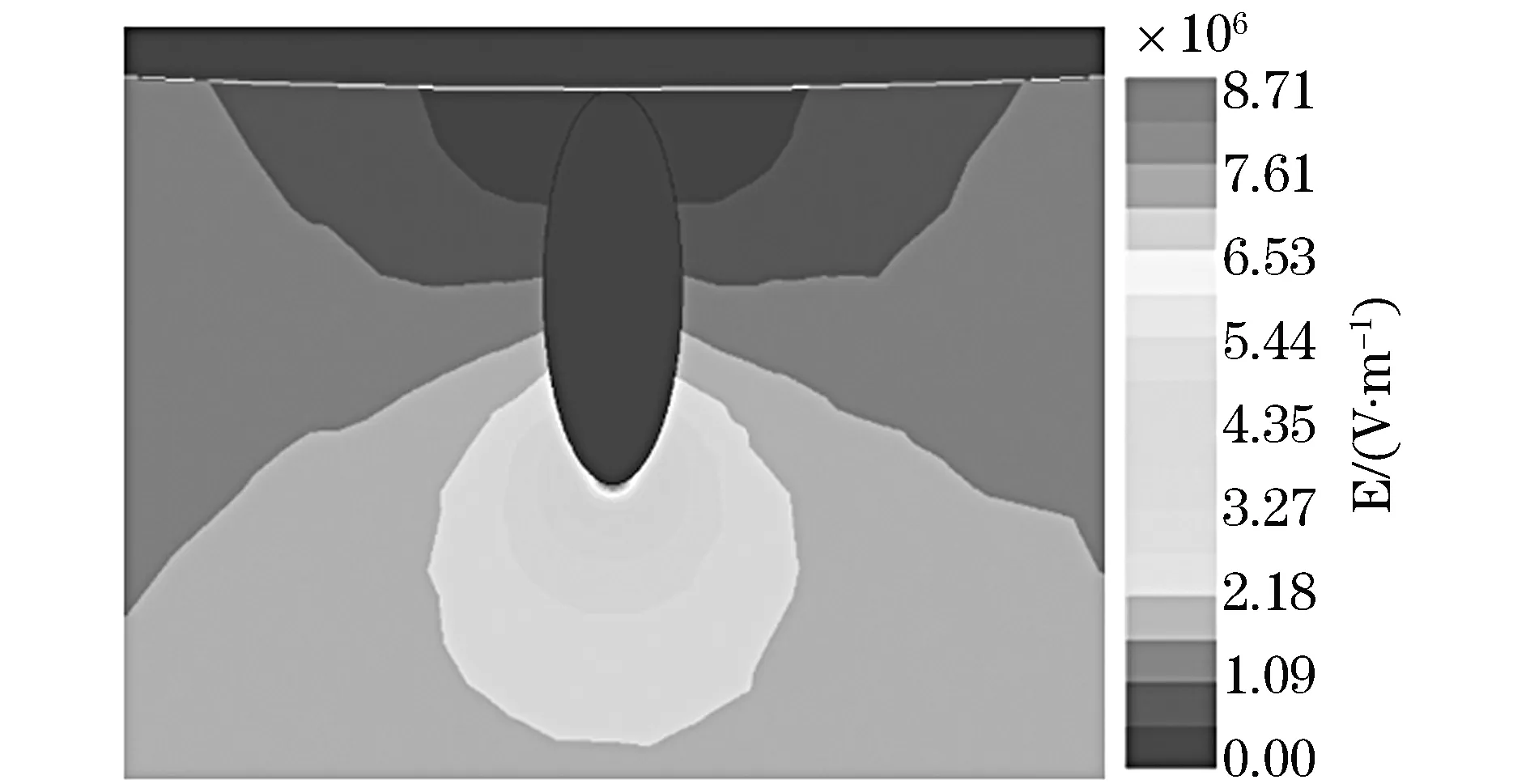
图3 椭圆形颗粒对电场的畸变云图(短轴140 μm，长轴400 μm)Fig.3 Cloud atlas of electric field distortion caused by elliptical particles (short axis 140 μm, long axis 400 μm)

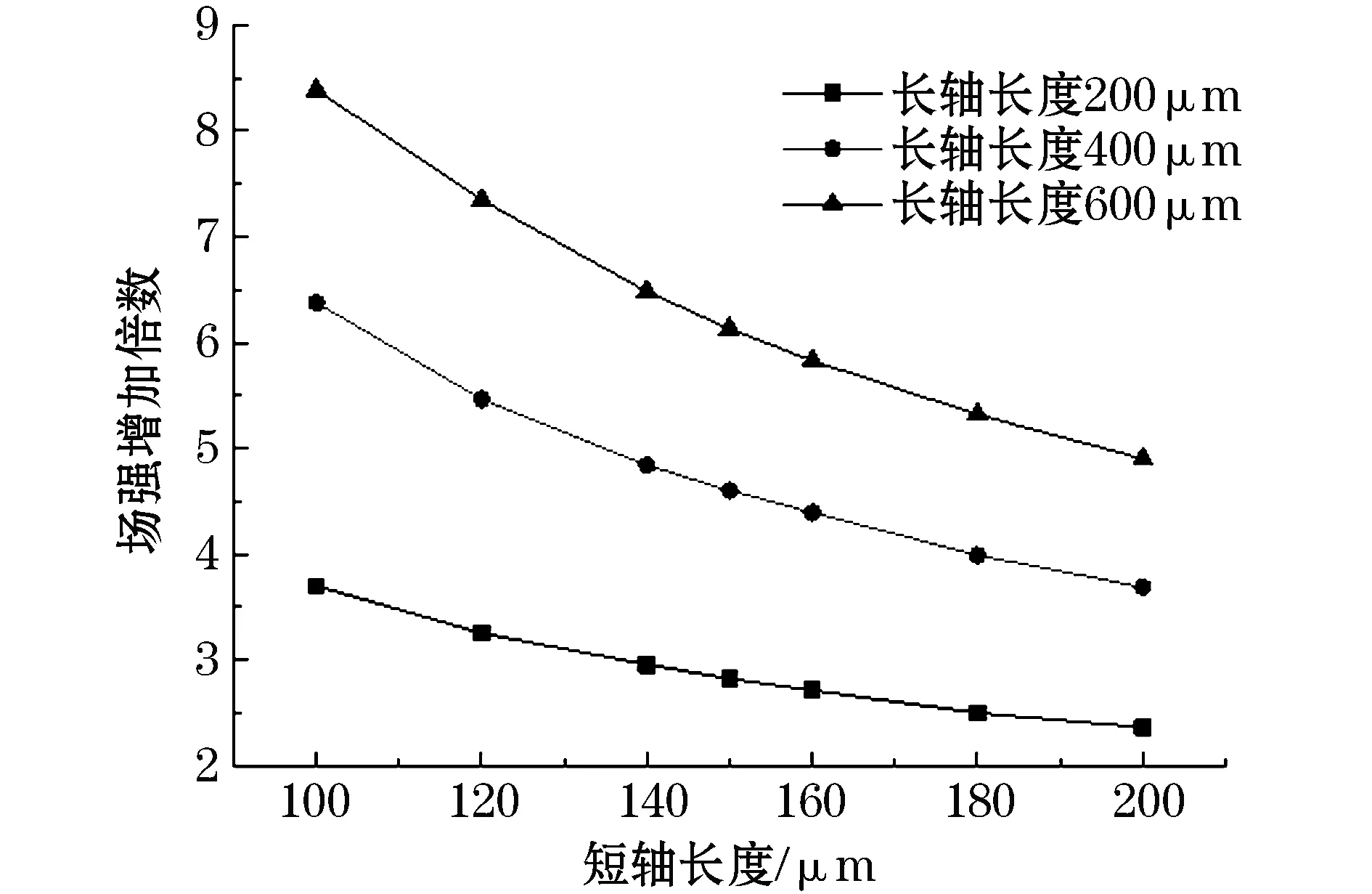
图4 顶部场强随短轴长度的变化(长轴恒定)Fig.4 Variation of electric field strength at the top of particles with the length of short axis(long axis is constant)

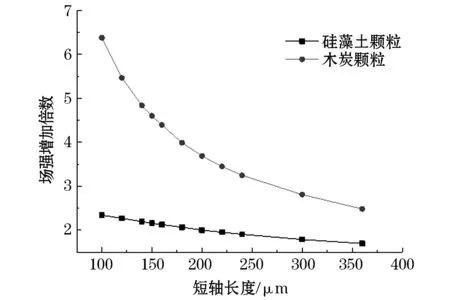
图5 不同颗粒物顶部场强随短轴长度的变化Fig.5 Variation of electric field strength at the top of different particles with the length of short axis

根据图中的仿真结果，得到以下结论：

1)当木炭颗粒物长轴长度恒定时，导线表面电场强度随颗粒物短轴长度的增加逐渐降低，最终趋于一恒定值。当木炭颗粒物短轴长度恒定时，导线表面电场强度随颗粒物长轴长度的增加而升高，即椭圆形颗粒物长轴长度与短轴长度比值越大，颗粒物顶部场强越大。

2)随着硅藻土颗粒长轴长度增加，颗粒顶部场强减小，但减小幅度较小；相对于硅藻土颗粒，木炭颗粒顶部场强随长轴长度增加下降较为显著。由图5仿真结果可知，木炭颗粒顶部最大场强为硅藻土颗粒顶部最大场强的3.58倍。

4.2 圆形颗粒物

圆形颗粒物的几何参数为颗粒直径r。圆形颗粒对电场的畸变云图如图6所示。由图6可以看出，圆形颗粒物对导线表面电场具有明显的畸变作用，畸变场强最大值出现在距离导线最远点，与椭圆形颗粒物相比圆形颗粒物畸变场强最大值范围较大，同时圆形颗粒物内部场强为零。当木炭颗粒物直径由20～200 μm等梯度变化时，颗粒物顶部电场强度与直径的关系如图7所示。导线表面附着不同种类圆形颗粒物时，顶部场强随直径的变化规律如图8所示。

图6 圆形颗粒对电场的畸变云图(直径200 μm)Fig.6 Cloud atlas of electric field distortion caused by circular particles (diameter 200 μm)

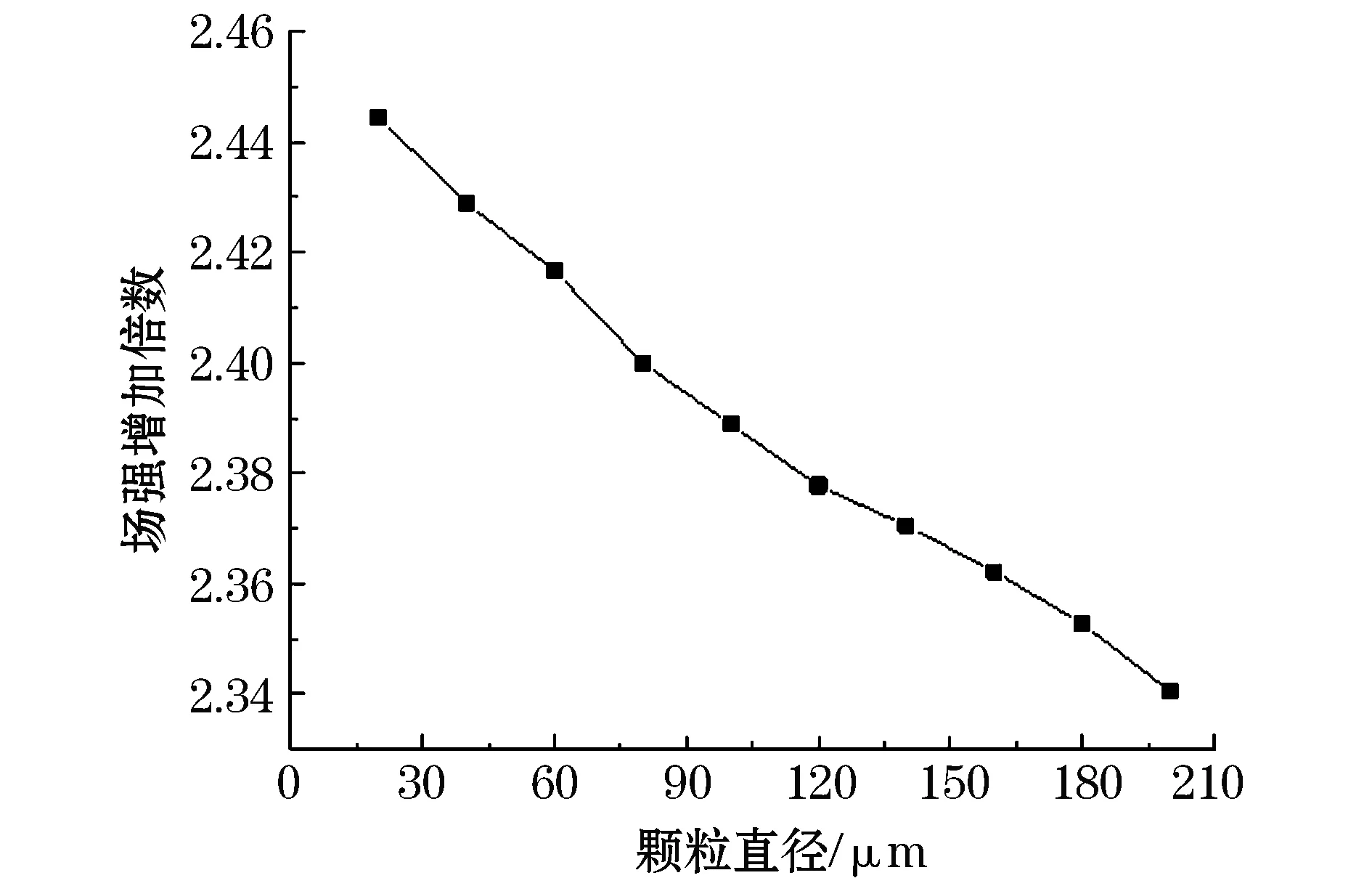
图7 顶部场强随直径的变化(其他参数恒定)Fig.7 Variation of electric field strength at the top of particles with diameter(other parameters are constant)

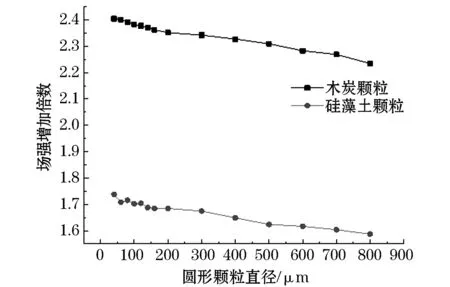
图8 不同颗粒物顶部场强随直径的变化Fig.8 Variation of electric field strength at the top of different particles with diameter

根据图中的仿真结果，得到以下结论：

1)随着圆形颗粒物直径的增加，颗粒顶部场强逐渐降低，颗粒顶部场强与颗粒直径呈线性关系。当圆形颗粒物直径为20 mm时颗粒顶部场强最大，最大场强可达标准值的2.44倍。

2)针对不同种类颗粒物，随着圆形颗粒直径增加，颗粒顶部电场强度均缓慢减小。当圆形颗粒直径在50～800 μm范围内时，直径每增加100 μm，顶部场强下降约0.23 kV/cm，并且木炭颗粒顶部场强为硅藻土颗粒顶部场强的1.4倍左右。

4.3 菱形颗粒物

菱形颗粒物的几何参数为颗粒对角线AC和BD，当菱形木炭颗粒对角线AC长度分别为200、250、300 μm恒定时，颗粒顶部场强随菱形颗粒物对角线BD长度的变化规律如图9所示。

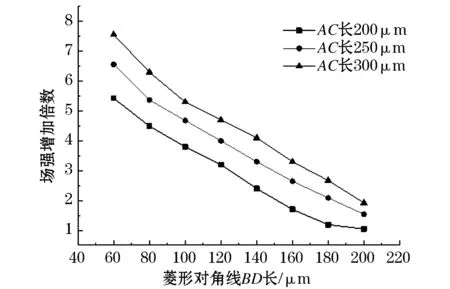
图9 颗粒物顶部场强随对角线长度的变化(其他参数恒定)Fig.9 Variation of electric field strength at the top of particles with diagonal length(other parameters are constant)

根据图9中的仿真结果，可以得到以下结论：

1)菱形颗粒物顶部场强随着颗粒对角线长度的增加逐渐降低，两者呈线性关系。

2)当颗粒物对角线AC长度恒定时，颗粒物顶部电场强度随颗粒对角线BD长度的增加逐渐降低。

3)当颗粒物对角线BD长度恒定时，导线表面电场强度随颗粒物对角线AC长度的增加而升高，即颗粒物顶部夹角越小，场强越大。因此，形状为针形的颗粒物对导线表面场强影响更严重。

4.4 颗粒物种类的影响

为研究颗粒物种类对导线表面电场强度的影响，分别对木炭颗粒、金属颗粒、硅藻土颗粒、蓝宝石颗粒以及高岭土颗粒进行仿真对比研究。假设颗粒形状均为椭圆形，5种颗粒物的电导率和相对介电常数如表1所示。颗粒种类变化时椭圆形颗粒物顶部场强的变化规律如图10所示。

表1 颗粒物参数表Table 1 Particle parameters

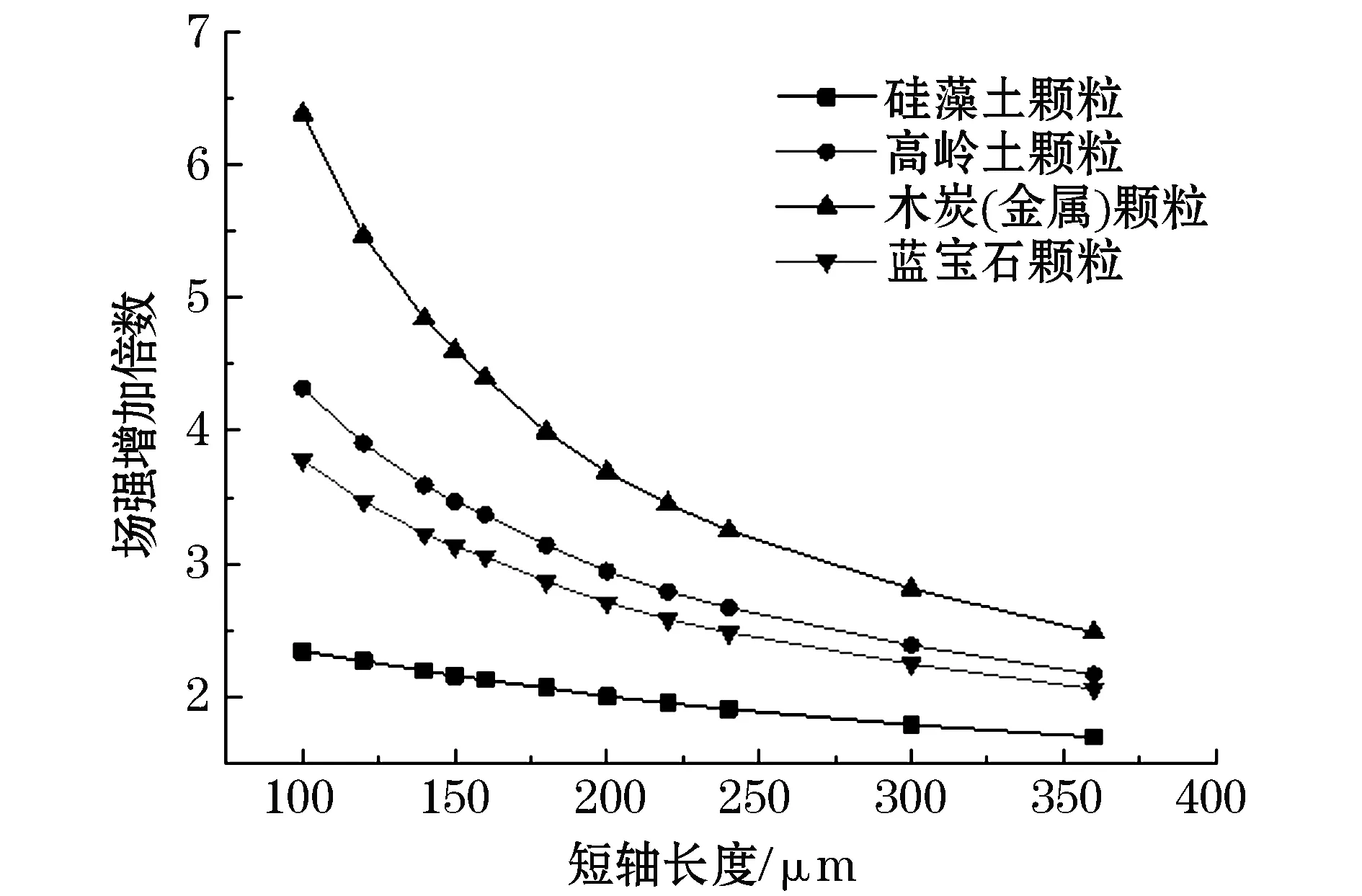
图10 不同颗粒物顶部场强随短轴长度的变化Fig.10 Variation of electric field strength at the top of different particles with short axis

根据图10中的仿真结果，可以得到以下结论：

1)不同种类导体颗粒物顶部畸变场强均相同，并且导体颗粒物顶部场强远大于绝缘颗粒顶部场强。因此，空气中木炭颗粒对电场的畸变更为严重。

2)对于绝缘颗粒，其相对介电常数越大，颗粒顶部畸变场强越大[19]。

4.5 颗粒物相对介电常数的影响

为研究颗粒物相对介电常数对导线表面场强的影响，仿真研究了椭圆形、圆形、菱形3种颗粒物在相对介电常数为1～15范围内等梯度变化时，颗粒物顶部场强随相对介电常数的变化关系。图11所示为颗粒物顶部场强随相对介电常数的变化曲线。

根据图11中的仿真结果，可以得到以下结论：

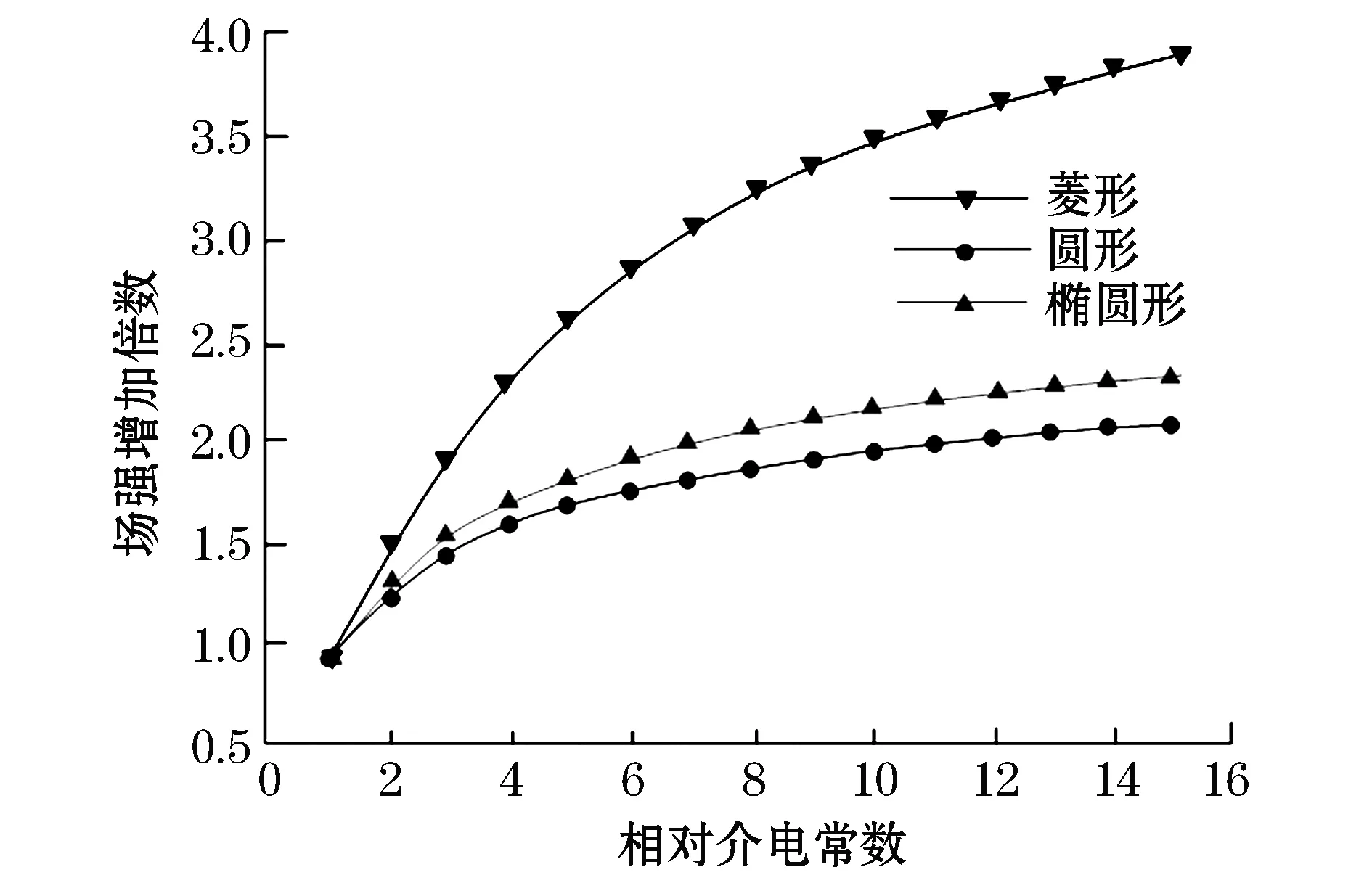
图11 颗粒物顶部场强随相对介电常数的变化Fig.11 Variation of electric field strength at the top of particles with relative dielectric constant

1) 绝缘颗粒物顶部场强均随相对介电常数的增加而增大。当颗粒物相对介电常数在1～7时，颗粒物顶部场强增加倍数变化较为显著；当颗粒物相对介电常数达到7以上时，颗粒物顶部场强增加倍数趋向于某一固定值。

2) 菱形颗粒顶部对电场的畸变情况最严重，椭圆形颗粒次之，圆形颗粒最小。因此要着重预防菱形颗粒物对导线表面电场的影响。

5 结 语

1)当直流导线表面附着颗粒物时，颗粒物顶部会产生畸变电场，使导线表面场强增加，最大增加幅度可达正常运行条件下的8倍左右。因此，必须考虑空气中颗粒物对导线表面场强的影响。

2)对于相同种类颗粒，不同颗粒几何形状对导线表面场强的影响不同。仿真研究的3种颗粒中，菱形颗粒顶部对电场的畸变情况最为严重，椭圆形颗粒次之，圆形颗粒最小。这说明颗粒物对电场的畸变程度与颗粒物几何形状相关。因此，在研究颗粒物对电场的畸变程度时，要着重考虑形状为针状的颗粒物。

3) 导体颗粒物顶部场强远大于绝缘体颗粒顶部场强；绝缘颗粒相对介电常数越大，颗粒顶部畸变场强越大，当颗粒物相对介电常数达到7以上时，颗粒物顶部场强增加倍数趋向于某一固定值。