基于geostudio库水位涨落和降雨作用下土坝渗流稳定分析

（长沙理工大学水利工程学院，湖南长沙 410004）

引言

降雨与库水位变动是影响滑坡稳定性的两个重要因素[1]。我国已建成的水库大坝有数十万座，其中约90%为土石坝，相关统计显示，由渗透破坏直接导致的土石坝工程失事概率，中国是29%（2 391 座失事）[2]。库水位涨落使岸坡内渗流场不断变化，从而使岸坡内的孔隙水压力场也处在不断的变化之中，进而影响到岸坡的稳定性[3]；降雨诱发滑坡失稳的主要原因是边坡土体抗剪强度降低（饱和区有效应力降低、非饱和区基质吸力降低、土体产生软化）和边坡作业荷载增加（土体湿度增加、重度增加、渗透力增加）。[4]

许多学者对库水位涨落和降雨进行研究。唐栋[5]在降雨实测资料下，研究了不同初始条件对不同土体边坡稳定性影响。王开拓[6]对均值土石坝在水位降落作用下的渗流稳定进行了分析，张珂峰[7]对边坡在降雨库水位下降联合作用下的渗流稳定进行了研究。类似的研究还有很多。

本文以文献[8]某土石坝为依托，利用geostudio 软件对上游库水位不同骤降速率、校核洪水位骤降至正常蓄水位不同速率以及不同降雨强度下的某土石坝的上下游坝坡的渗透稳定性进行了数值模拟，为此土石坝在库水位骤降和降雨工况下的运行安全稳定提供参考。

1 计算理论

1.1 非饱和渗流理论

前人研究表明，达西定律不但适用于饱和土渗流计算，同时还能描述非饱和土中水的流动现象。方程中的渗透系数不再是常数，而是与含水量有关的变量。非饱和土渗流表达式为：

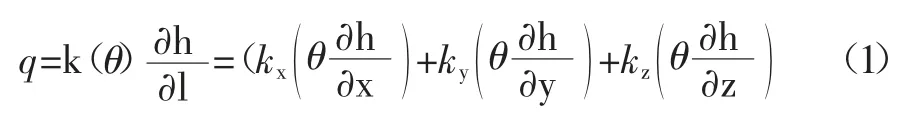
其中，q 为体积流量；k（θ）为渗透系数；h 为土体水势能梯度。文章考虑各向同性土下的降雨二维渗流工况，即只有水平向和竖直向的渗流，两个方向的渗透系数相等。

1.2 非饱和土抗剪强度理论

在水位下降和降雨作用下，坝体内饱和区域和非饱和区域一直处于变动的状态中，降雨可以使得地下水位以上岩土体出现暂态饱和区，降低岩土体的抗剪强度[9]。库水位涨落使得坝体某些饱和区域变成非饱和区域。根据相关研究，本文采用Fredlund 双应力变量公式[10-12]。

式中：c′与φ′为有效强度参数；σn为法向总应力与孔隙气压力的差值；ua为孔隙空气压力；uw为孔隙水压力；φb为由负孔隙水压力而提高的强度。

1.3 边坡稳定性理论

边坡稳定性分析利用极限平衡法。传统的极限平衡法有瑞典圆弧法、Bishop 法、简布法、不平衡推力传递法、斯宾塞法以及Morgenstern-Price 法（简称M-P 法）等。M-P 法适用于任意土分布、任意滑动面形状，满足静力平衡和力矩平衡，计算精度高。本文使用M-P 法进行土石坝的稳定性分析。

2 计算模型

2.1 计算模型及边界条件

某土石坝正常蓄水位97.50 m，死水位77.50 m，校核洪水位100.50 m，大坝最大坝高为30.45 m，坝顶高程103.45 m，坝顶宽5 m。为简化计算，模型高度为70 m，其中坝体高度30 m，坝顶宽度5 m，模型长度285 m，其中坝体长度185 m。迎水坡、背水坡坡度均为1∶3。在坝体迎水坡选取A（126.4，19.0）、B（84.0，5.3）监测空隙水压力的变化，在背水坡选取C（154.0，24.9）、D（193.7，9.4）监测空隙水压力的变化。模型剖面如图1所示，计算单元为四边形单元与三角形单元。模型网格尺寸约为2 m，一共划分为3 727 个节点，3 582 个单元。将左侧为定水头时的稳态计算结果作为初始条件。边界条件为：bc、cd 为定水头边界，ah 为不透水边界，de、ef 为降雨入渗边界，由于降雨强度小于土体饱和时的渗透系数，降雨用单位时间流量计算，fg 为零压力边界。

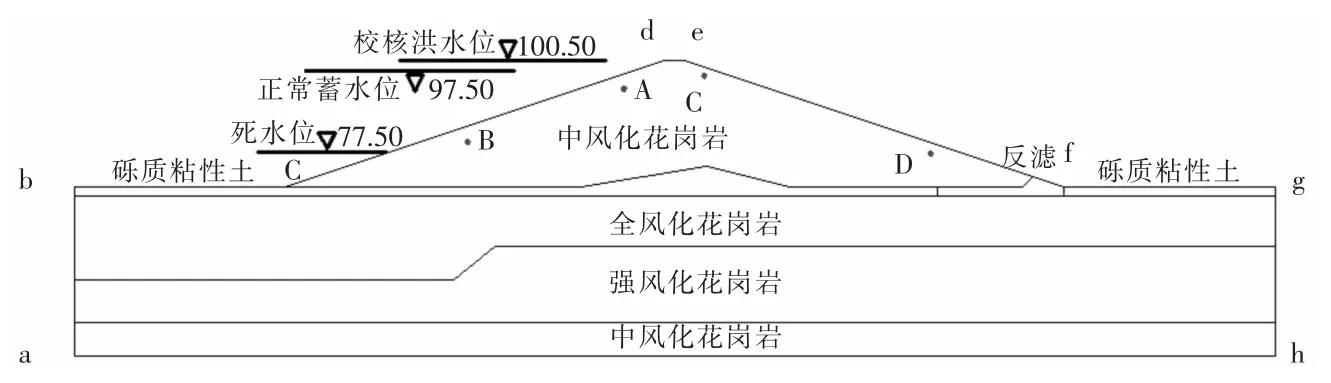
图1 计算模型

2.2 土体参数

各土层物理参数如表1 所示，力学参数如表2 所示。

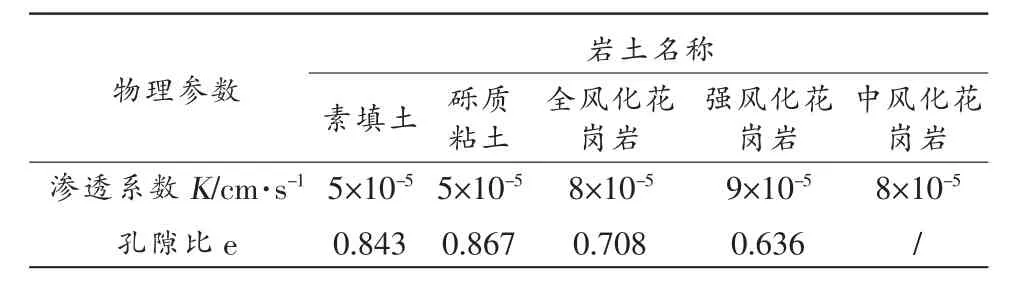
表1 各岩土层物理参数数值表

表2 各岩土层物理力学参数取值表

其中素粘土选用饱和-非饱和模型，其余各土层选用饱和模型，非饱和土体体积含水量函数采用Seep/w自带的粘土含水量函数，渗透系数函数利用Van Genuchten 函数拟合，得出其土水特征曲线和渗透系数函数曲线。

2.3 计算工况

为进一步研究库水位和降雨作用下滑坡的渗流特性以及稳定性规律，本文取不同速率正常蓄水位骤降至死水位、不同速率库水位上升以及正常蓄水位下不同降雨强度三种工况分别进行计算分析，计算工况如表3 所列。

3 计算结果分析

3.1 不同速率正常蓄水位骤降至死水位

3.1.1 孔隙水压力变化规律

正常蓄水位骤降至死水位情况下的不同监测点A、B、C、D 的孔压变化如图2 所示。由图2 可知：总体来说，A、B、C、D 四点的孔隙水压力呈先减小后基本保持不变的趋势。对于同一个点，水位下降速率越大，孔隙水压力的下降幅度越大，速率越快。对于上部监测点A、C，孔隙水压力达到稳定的时间越长；对于下部监测点B、D，孔隙水压力达到稳定的时间相对较短。孔隙水压力的下降幅度与监测点位置相关，迎水坡孔压的降幅总体上要大于背水坡。

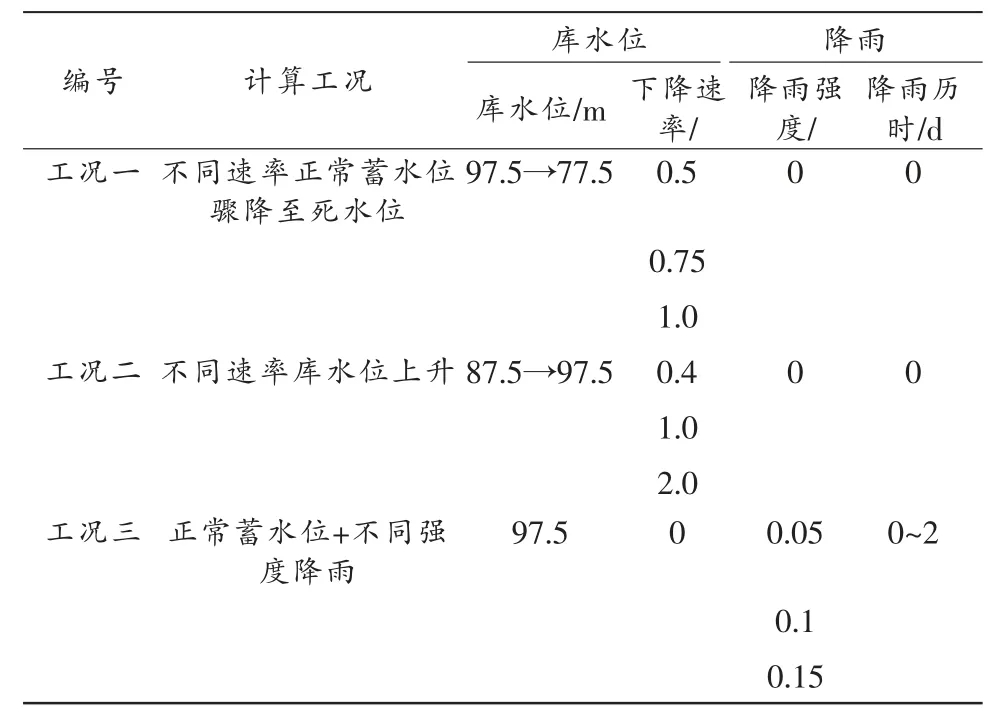
表3 计算工况

3.1.2 稳定性变化规律

正常蓄水位骤降至死水位情况下的迎水坡、背水坡稳定性变化如图3 所示。迎水坡安全系数呈先快速下降然后小幅上升最终趋于稳定的趋势；背水坡安全系数呈先上升后趋于不变的趋势；且上下游坝坡的最终安全系数趋于一致。

3.2 不同速率库水位上升

3.2.1 孔隙水压力变化规律

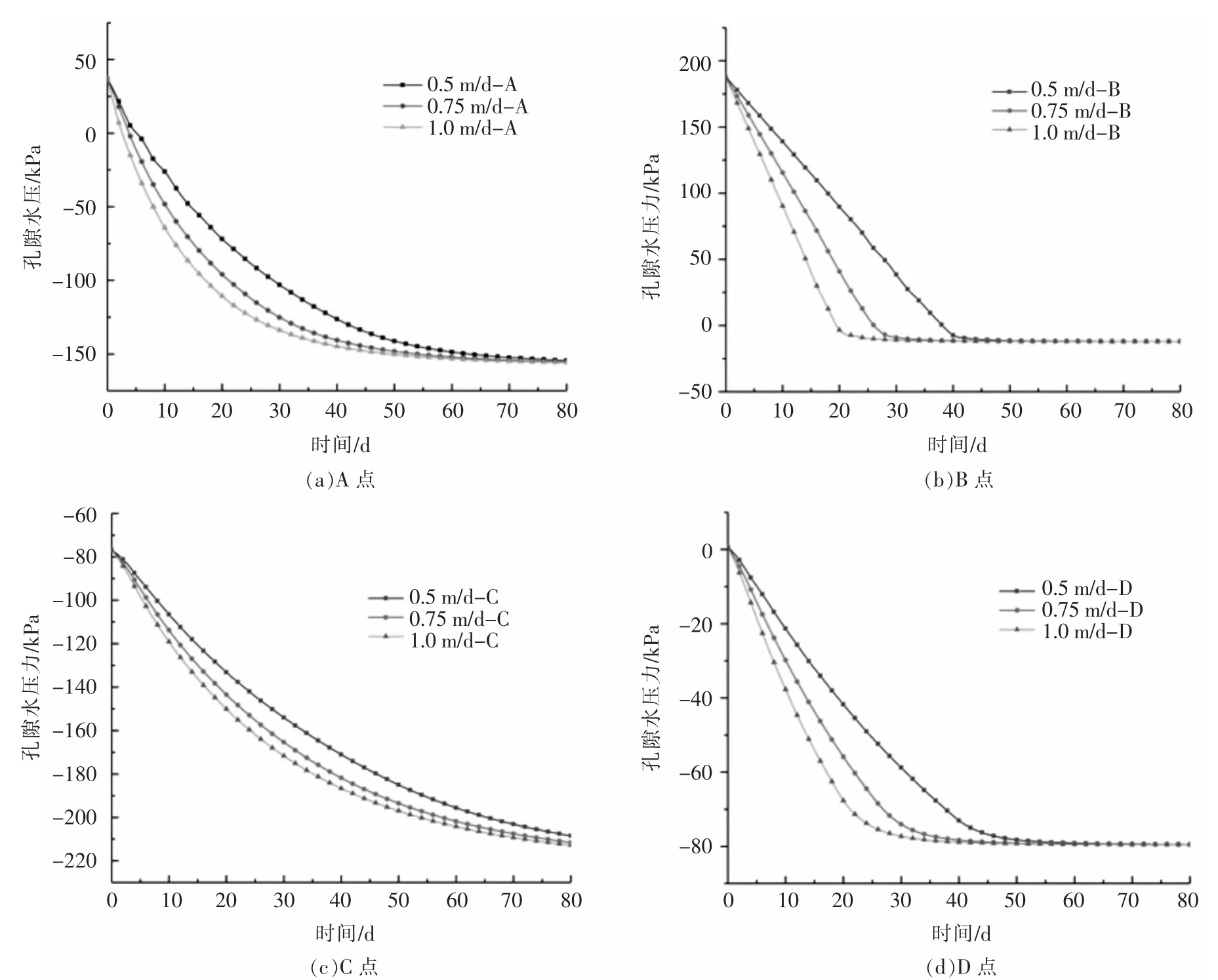
图2 工况一孔压变化图

不同速率库水位上升情况下的不同监测点A、B、C、D 的孔压变化如图4 所示。由图4 可知：总体来说，A、B、C、D 四点的孔隙水压力呈先增大后基本的保持不变得趋势。对于同一个点，水位上升速率越大，孔隙水压力的上升幅度越大，速率越快。对于上部监测点A、C，孔隙水压力呈“折线型”变化，对于下部监测点B、D，孔隙水压力呈“S 型”变化。迎水坡孔压的增幅总体上要大于背水坡。

3.2.2 稳定性变化规律

不同速率库水位上升情况下的迎水坡、背水坡稳定性变化如图5 所示。迎水坡安全系数呈先快速上升然后小幅下降最终趋于稳定的趋势；背水坡安全系数呈先下降后趋于不变的趋势。水位上升速率越快，对应的安全系数下降速率也越快。

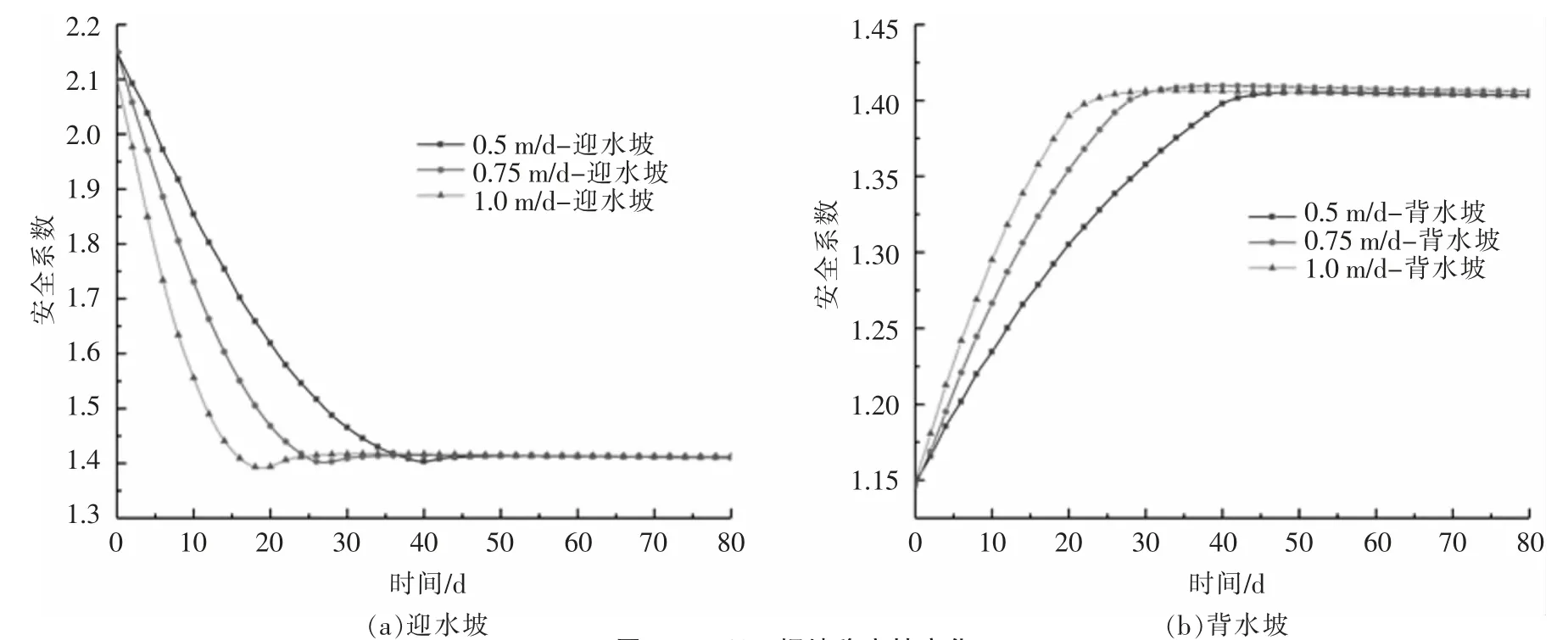
图3 工况一坝坡稳定性变化

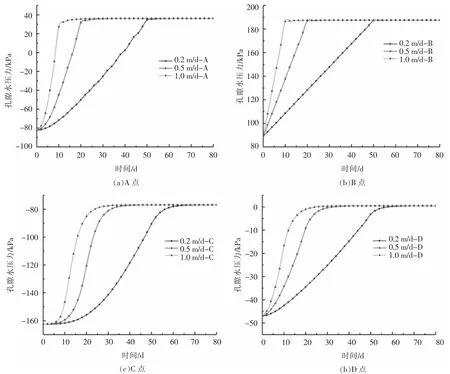
图4 工况二孔压变化图

3.3 正常蓄水位+不同强度降雨

3.3.1 孔隙水压力变化规律

正常蓄水位+不同强度降雨情况下的不同监测点A、B、C、D 的孔压变化如图6 所示。

由图6 可知：A、B、C、D 4 点的孔隙水压力呈先增大后减小最后趋于稳定的趋势；降雨强度越大，孔隙水压力上升幅度越大，但最后趋于一致。

迎水坡A、C 2 点的空隙水压力变化幅度很小；B、D 2 点孔隙水压力的变化幅度相对较大，说明在降雨情况下背水坡的孔压变化比迎水坡大；对于同一坡面，A 的孔压变幅大于B，C 的孔压变幅大于D，说明降雨引起的孔压变化与坝体内部高程有关，高程越高的点的孔压变化受降雨的影响越大。

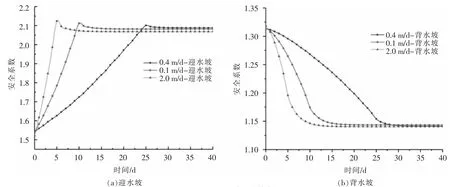
图5 工况二坝坡稳定性变化

图6 工况三孔压变化图

3.3.2 稳定性变化规律

正常蓄水位+不同强度降雨条件下的上下游坝坡稳定性规律如图7 所示。由图7 可知：迎水坡安全系数呈现随时间先下降后上升最后保持不变的趋势，在降雨过程中呈现下降的趋势，等降雨结束后安全系数开始上升直至稳定；安全系数变化幅度很小。背水坡总的变化趋势与迎水坡类似，也为降雨过程中安全系数下降，降雨结束后安全系数上升至稳定；安全系数变化幅度相对较大。说明降雨对背水坡的稳定性影响更大。

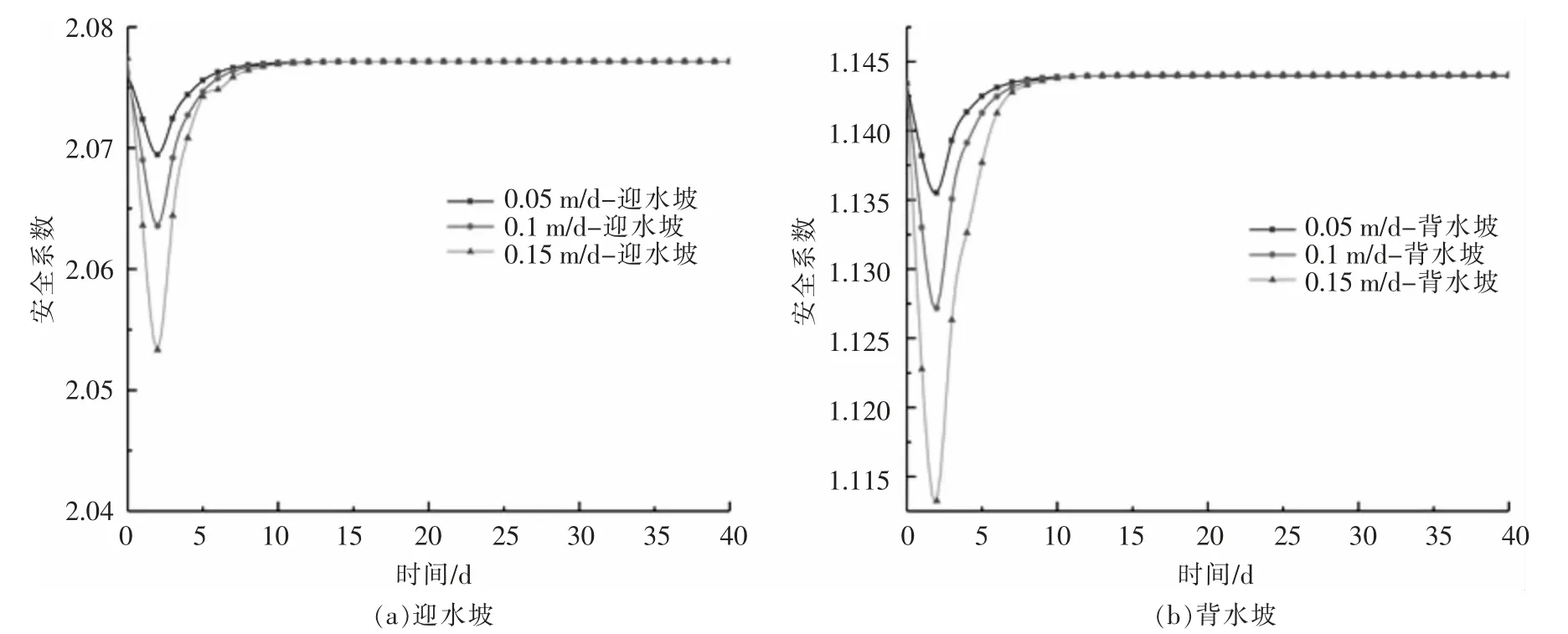
图7 工况三坝坡稳定性变化

4 结论

1）库水位下降工况下迎水坡孔压的下降幅度与库水位降落高度所对应的水压相当，迎水坡孔压变化幅度大于背水坡。迎水坡安全系数减小32.60%后略有增大后趋于稳定；背水坡安全系数增大22.10%。库水位下降速率越快，迎水坡安全系数下降越快，最小安全系数越小，背水坡安全系数上升越快。

2）不同速率库水位上升工况下，迎水坡孔压呈“折线型”变化，背水坡孔压呈“S 型”变化，迎水坡孔压增幅大于背水坡。迎水坡安全系数上升了35.00%，背水坡安全系数下降了13.50%，库水位增幅越快，迎水坡安全系数上升速率越快，背水坡下降速率越快。

3）正常蓄水位加降雨工况下背水坡的孔压变化比迎水坡大，高程高的点的孔压变化比高程低的点大，降雨强度越大，孔压上升幅度越大。降雨强度为0.15 m/d 时，背水坡安全系数下降了2.80%，此时安全系数处于“危险状态”；迎水坡安全系数变化幅度较小。

4）对于库水位涨落工况，分析得出：库水位降落对背水坡稳定有利，对迎水坡稳定不利；库水位上涨对迎水坡稳定有利，对背水坡稳定不利。对于降雨情况，降雨期间背水坡的安全系数容易出现“危险”状态。在实际工程中，需根据大坝运行的具体情况做好迎水坡、背水坡的安全加固工作，并做好相应的应急处置措施。