基于时空聚集的网贷反欺诈建模与研究*

2020-03-16俞旭峰张子柯

网络安全与数据管理 2020年2期

俞旭峰，王澎，郭威，张子柯

(1.杭州师范大学阿里巴巴复杂科学研究中心，浙江杭州 311121；2.阿里巴巴集团新零售技术事业群，浙江杭州 310008)

0 引言

网贷具有以下3个重要的优势：高回报、覆盖面广、需求量大[1]，所以最近几年得到持续蓬勃发展。然而，网贷在给借贷者带来便利、及时的金融服务的同时，也给放贷方带来了欺诈者的攻击威胁的风险[2-3]。首先，网贷主要是面向那些没有抵押、在传统信贷体系之外的借贷者；其次，网贷业务中个人数据较敏感，放贷方难以充分获取用户真实数据，所以那些缺少较为全面的反欺诈风控机制的放贷方面临着重大损失的风险[2-4]。

目前，国内外已有不少文献从不同角度来展开网贷反欺诈研究。如文献[5]总结了信用卡风险控制领域常用的统计方法，包括信用卡统计、信用卡债务、信用评分和信用评分率、平均信用卡债务等；文献[6]分析了借贷者社交网络与贷款欺诈的关系；文献[7]提取了贷款者的照片来分析网贷是否成功；文献[8]分析了贷款人的描述性文本对网贷是否成功和欺诈概率的影响；文献[9]使用被提取的贷款者行为欺诈图特征去预测网贷的欺诈概率；文献[10]发现了手机使用情况与网贷欺诈的相关性。

本文从特征探索的角度出发，对欺诈行为尤其是团伙欺诈行为的贷前预测进行了探索。首先，利用网贷场景下普遍存在的放贷时用户授权的空间位置与放贷时间，根据团伙欺诈时空聚集的行为特性，提出了一个实用、简洁的聚集指标——K-N最近邻指数；然后，对K-N最近邻指数进行序列学习；最后结合监督学习模型LightGBM[11]，对贷款进行欺诈预测。

1 坏账时空特性分析

1.1 数据描述

本文的网贷交易数据为国内某互联网公司的统计数据。网贷数据的时间长度为61天。交易数据仅包含申请成功且具有标签的贷款，记录无误的贷款数为216 470笔，其中坏账为2 654笔，总体的坏账率约为1.226%。放贷时的GPS定位精度为小数点后两位。具体数据字段如表1所示。

表1 网贷的特征

1.2 坏账时空分析

本文对前53天贷款数据进行分析，后8天贷款数据作为测试集。在数据集的特征探索中，特别分析了前53天坏账量最大的城市——西安的贷款分布状况。

图1(a)为西安第39天(当日城市坏账率为1.85%)的贷款空间分布情况。灰色点表示坏账率为0的区域(单位大小为1 km2),黑色点表示坏账率为100%的区域(单位大小为1 km2)，点的大小表示贷款量(该图中小点为1笔，大点为2笔)。当日西安仅产生了1例坏账，贷款的分布都较为随机。

图1(b)为西安第43天(当日城市坏账率为18.03%)的贷款空间分布情况，灰色点表示坏账率为0的区域(单位大小为1 km2),标记为“T”黑色点表示坏账率为82%的区域(单位大小为1 km2)，普通黑色点表示坏账率为100%的区域(单位大小为1 km2)，点的大小表示贷款量(该图中小点为1笔，大点为11笔)，除去非常异常的(108.95°E,34.29°N)区域(图中标记为“T”黑色点)后与图1(a)相似，贷款的分布较为随机且整体坏账率较低。

图1 西安不同日期的贷款空间分布

正常贷款行为是较为随机的，但欺诈行为往往时空集中、具有团伙性。如图2所示，该图上半部分表示西安地区每日的坏账率，下半部分表示西安地区前53天贷款量排名前三的区域(区域大小为1 km2)的每日所有贷款量与坏账量，点的大小表示该类贷款的数量。在贷款量排名前三的区域存在一个明显坏账空间集中的区域(108.95°E,34.29°N)，该区域存在55笔坏账(占西安总坏账的51.89%)。而且该区域坏账爆发时间也较集中，主要在第40～44天与第48～51天的时间段。

2 反欺诈建模

考虑到坏账之间异常的聚集关系，本文提出了K-N最近邻指数，一个能衡量贷款在某一阶段的空间聚集性指标。另外，本文中的观察窗口指的是观测贷款发生前的时间段。下文中“t天观察窗口内观测点的邻近点”含义是在观测贷款放贷发生的前t天内附近贷款的空间位置。

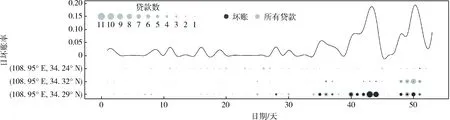
图2 西安的日坏账率与贷款量排名前三区域的贷款情况

2.1 K-N最近邻指数

最近邻分析概念[12]最初是由CLARK P J和EVANS F C提出的，用于比较区域内植物聚落情况。具体地，假定所有的点完全随机分布，则其平均距离为其密度倒数值的一半。该结果与借助图像观测到的实际的点分布格局的比值通常叫做最近邻指数(nearest neighbor index)[13]。

最近邻指数反映了一个区域内点之间的聚集程度，体现的是全局的聚集状况。受最近邻指数的启发，本文改进得到了K-N最近邻指数，能反映单个点局部相对聚集情况。

K-N最近邻指数的设计概念如下：

观测点与邻近点的空间示意图如图3所示。图3(a)与图3(b)中点的含义相同，圆点为观测点(观测贷款的位置)，三角形为一定时间大小的观察窗口内观测点的邻近点(邻近贷款的位置)。图3(a)根据包含邻近点的个数先后建立两个大小不一的邻近域S1、S2。S1包含k个邻近点，S2包含n个邻近点(n>k)。通过图3(a)的S2中n个邻近点可以组成图3(b)的封闭图形。

图3 观测点与邻近点的空间示意图

根据图3(a)中S2包含的n个邻近点是否能组成封闭图形分成以下两种情况：

(1)n个邻近点能组成封闭图形，如图3(b)所示，S1内k个邻近点与观测点距离的平均值D，S2内n个邻近点随机情况的平均最近邻距离E(随机情况下平均最近邻距离为其密度倒数值的一半[13])，两者的比值表示观测点的邻近相对聚集情况。

(2)n个邻近点不能组成封闭图形。可能存在的极端情况，即n个邻近点无法形成封闭的图形，呈现的几何状态为绝大数邻近点集中于某一点或者连接成一条线。此类情况本身就是非常聚集的表现，但又很难采用特定的数值进行定值。该极端情况下，本文将观测点的K-N最近邻指数得分定为“空值”。因为最终预测模型为LightGBM模型，该集成树算法在树节点进行选取最佳特征分裂点时将缺失值样本分别置于左右叶子节点，最终选择分裂增益最大的方向。所以本文将极端情况处理为“空值”，在不失其特性的情况下也是适用于最后的预测。

t天观察窗口内某观测点的K-N最近邻指数具体计算步骤如下：

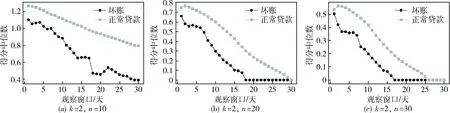
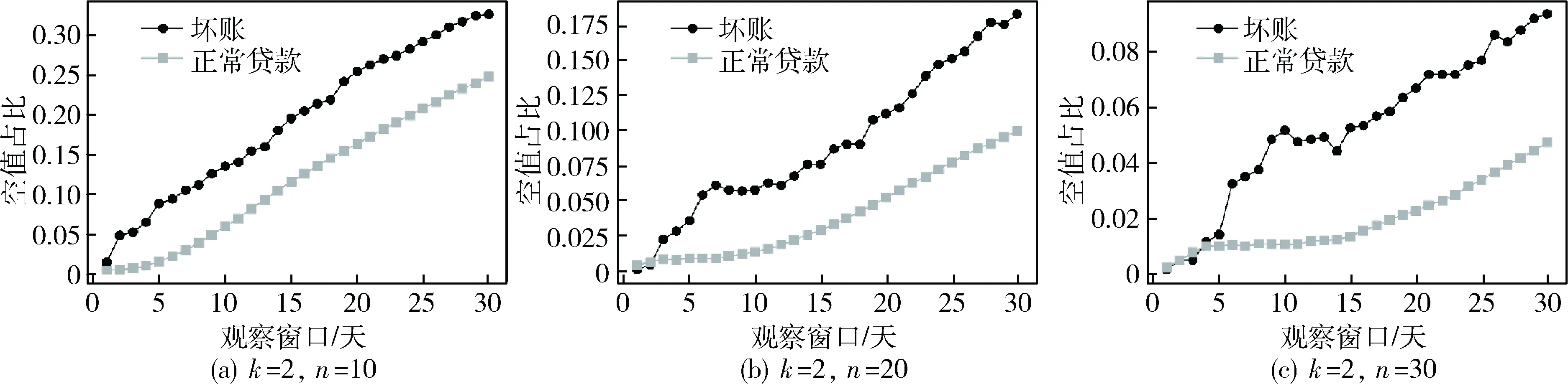
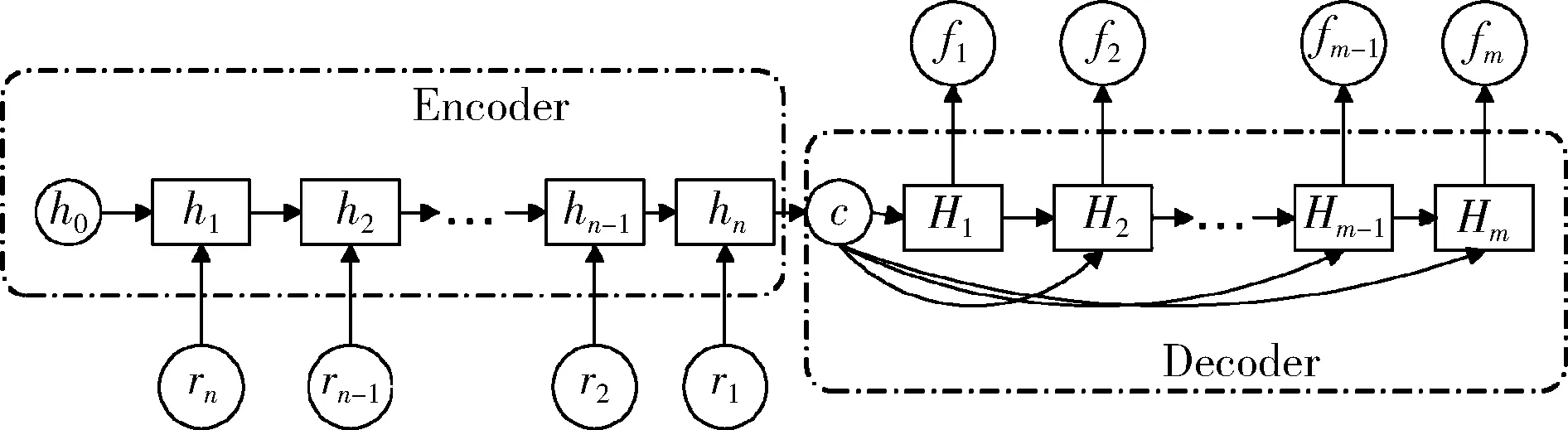
(1)观测点放贷发生的前t天观察窗口内，计算观测点空间最近邻的k笔贷款(k

(1)

其中，k为t天观察窗口区域内S1内邻近点数量，di为观测点与观察窗口内S1内邻近点的距离。

(2)观测点放贷发生的前t天观察窗口内，S2内n个邻近点形成如图3(b)所示的凸包[14]，按最近邻指数的定义[13]，计算凸包内(包括边缘)随机情况下整个区域内邻近点最近邻距离的平均距离E:

(2)

其中，n为t天观察窗口区域内S2内邻近点数量，A为观察窗口内S2内全部邻近点所围成凸包的面积。如图3所示，通过对邻近点的凸包计算[14]得到面积A。

(3)计算K-N最近邻指数r：

r=D/E

(3)

较低的r得分表现为观测点距离观察窗口内的邻近点相对较为接近，观测点与邻近点相对更为聚集。

以第31～53天的贷款作为观测贷款，观察窗口大小范围为1～30天。控制不同的观察窗口t、k值与n值，K-N最近邻指数都能很好地区分坏账与正常贷款，具体分析如下：

设置K-N最近邻指数中k=2，n=20。如图4所示，按观察窗口的时间长短，从短到长取了5天、15天、25天的观察窗口，坏账在K-N最近邻指数低分区域的占比都很明显大于正常贷款。不同观察窗口下，坏账更容易得到较低的K-N最近邻指数得分。

图4 不同观察窗口下的K-N最近邻指数的得分累计分布

图5、图6反映了不同n值、k值对坏账与正常贷款的K-N最近邻指数得分中位数的影响。K-N最近邻指数得分中位数会随着n值增大而减小，随着k值增大而增大，但坏账的得分中位数都明显低于正常贷款。

图7反映了改变n值对坏账与正常贷款的K-N最近邻指数得分的空值占比的影响。K-N最近邻指数得分的空值占比随着n值增大而减小，但坏账的空值占比都明显高于正常贷款。坏账的邻近点更容易无法形成封闭图形。

所以在较为合适的观察窗口t、k值与n值情况下，K-N最近邻指数对坏账与正常贷款有较好的区分能力。

同一个观察点不同观察窗口下存在聚集变化，为了进一步提取不同窗口下K-N最近邻指数的序列信息，本文以基于LSTM的seq2seq模型学习K-N最近邻指数序列得到最终向量来表征聚集变化。

2.2 K-N最近邻指数的序列特征

seq2seq模型[15]最初使用于自然语言处理领域，核心思想是通过深度神经网络模型将一个作为输入的序列映射为一个作为输出的序列。该模型最初采用的深度神经网络模型为RNN。而LSTM在RNN基础上进行了提升，使其能够获取到更长距离的信息，从而学习到长依赖的特征[16]。

图5 不同n值时的K-N最近邻指数中位数

图6 不同k值时的K-N最近邻指数中位数

图7 不同n值时的K-N最近邻指数空值占比

根据不同时间间隔的贷款对当前贷款作用强弱不同，将不同观察窗口的K-N最近邻指数，按观察窗口的长短从大到小组成相应的序列L1={rn,rn-1，…,r2,r1}，并输入到第一个LSTM模型组成的编码器(Encoder)。如图8所示，编码器隐藏层状态为：

ht=f(ht-1,rn-t+2)

(4)

其中，c包含了输入序列L1编码后的信息，第二个LSTM模型组成的解码器(Decoder)的隐藏层状态为：

Ht=f(Ht-1,ft-1,c)

(5)

最后，控制一定的维度数m，将解码器的隐藏层组成输出序列L2={f1,f2,…,fm-1,fm}。L2序列作为L1序列的embedding结果。L2序列存在原序列L1元素间的交互信息，作为新特征对原模型进行提升。

图8 基于LSTM的seq2seq模型

3 实验与结果分析

本文利用表1的特征进一步建立了如表2所示的基础特征。

表2 模型的基础特征

模型评估采用KS值与AUC。AUC反映的是模型对测试样本整体的预测能力。作为风控建模中最为常见的指标，KS(Kolmogorov-Smirnov)值适用于正负样本极其不平衡的场景，衡量的是好坏样本累计分布之间的差值。好坏样本累计差异越大，KS值越大，那么模型的风险区分能力越强。

本文将第31～53天作为训练集，第54～61天作为测试集，利用LightGBM模型对第31～53天网贷数据进行训练，然后对第54～61天网贷数据进行预测输出欺诈概率。设置K-N最近邻指数中k=2，n=20，观察窗口t为1～30天，得到不同观察窗口下相应的一系列K-N最近邻指数r1～30。为了能使用seq2seq模型提取embedding特征又能满足序列的完整性，权衡考虑之下，此时对K-N最近邻指数空值进行了“-1”填充，控制输出维度在m=5的情况下有了较好的提升。K-N最近邻指数预测效果如表3所示。