新型系泊机构气动控制分支建模及摩擦力补偿试验研究
2020-03-14张伟李淳潮李志远尚尧
张伟 李淳潮 李志远 尚尧
(1.燕山大学 河北省重型机械流体动力传输与控制重点实验室,河北 秦皇岛 066004;2.燕山大学 机械工程学院,河北 秦皇岛 066004)
随着海运事业的发展,码头作业基本实现了自动化,但缆绳系泊这一方式没有发生质的飞跃[1]。目前,国外Cavotec公司研发的MoorMaster200通过机械臂与吸附于船体的真空吸盘来代替缆绳的功能[2]。Docklock公司研发的系泊系统通过机械臂和电磁吸盘来满足不同出力需求[3]。Rosa-Santos等[4]从减少系泊船舶运动和改善泊位运行安全条件的角度,提出的张力系泊有防止共振的效果。国内虽已申请自动系泊的相关专利[5- 6],但在自动系泊装置的应用上被国外企业垄断[7]。
文中的新型智能系泊装置样机采用气动独立负载口控制方式的双并联机构,以实现系泊智能化为目的,自动接舶、减摇为基本要求。在接舶时,由于难以避免的摩擦力[8],若想实现精确定位必须对摩擦力进行补偿。
在气缸摩擦力补偿方面常用的方法有:改变润滑状态,采用复杂的近代控制策略,叠加高频低幅的颤振信号等。Chang等[9]通过改变润滑剂的材料来降低摩擦力,改善了粘滑现象。魏琼等[10]采用双观测器估计摩擦力和非线性自适应反步摩擦控制方法,减少了气缸在低速工况下的爬行。智淑亚等[11]设计了一种基于遗传算法的模糊补偿控制器,仿真实验结果表明,此方法不仅可以有效抑制系统的爬行现象,而且可以提高系统的动态性能。孔祥臻等[12]在基于Stribeck摩擦力模型的比例方向阀阀控缸的控制信号中叠加高频低幅的控制信号,证明了高频信号可以克服部分摩擦力。
文中对比例压力阀独立负载口位置控制系统进行了详细分析,给出了系统的数学模型,并基于一腔恒压力、一腔位置闭环的控制方式,提出了在恒压腔压力阀控制信号上叠加高频颤振信号的摩擦力补偿方法,并进行了实验验证。
1 单个驱动分支的模型
文中的新型智能系泊装置样机如图1所示。单个机构由3条气缸驱动,气动系统原理如图2所示。气动分支均采用比例压力阀独立负载口的控制方式对上平台的重力负载进行平衡[13]。单个驱动分支是整个气动控制系统模型的基础,首先建立单个驱动分支的数学模型。
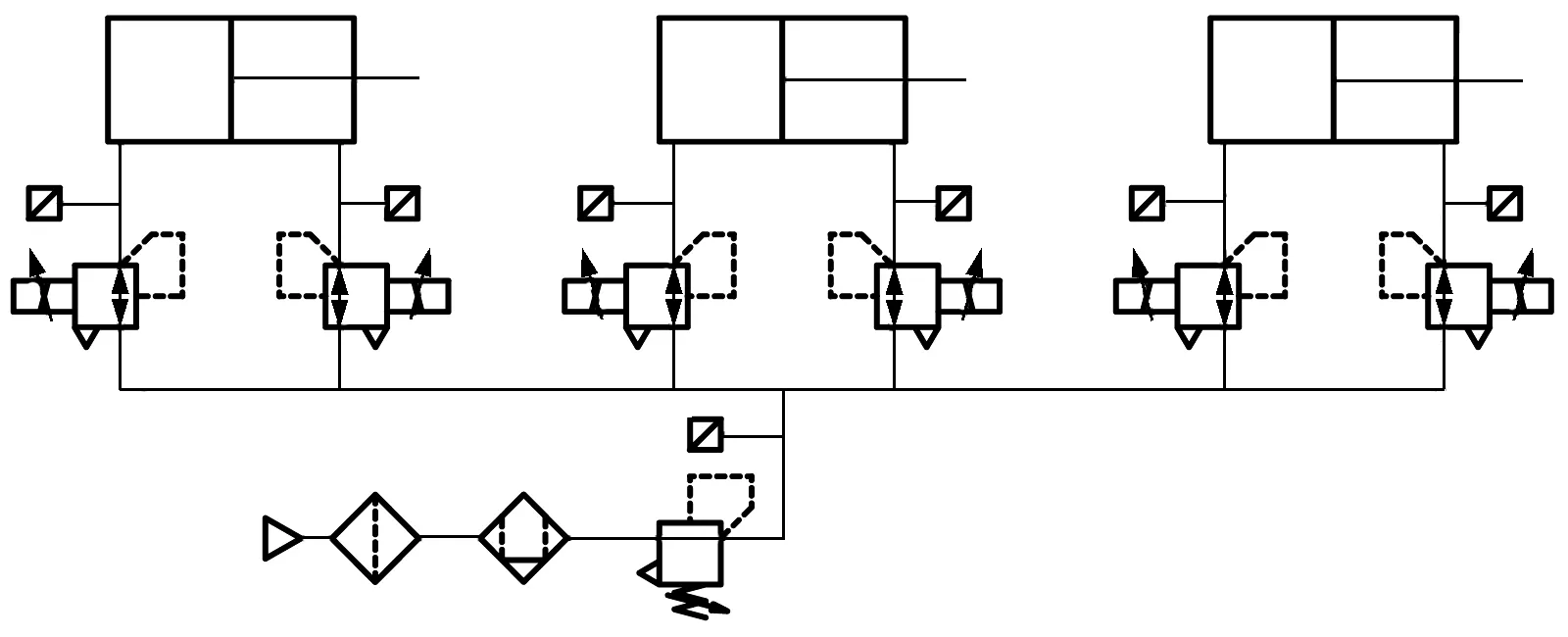
图2 系泊样机气动控制系统原理图
Fig.2 Schematic diagram of pneumatic control system of moo-ring prototype
1.1 比例压力阀模型
气动驱动分支采用的控制阀为电/气比例压力阀,比例阀的出口压力与输入控制信号成正比。
1.1.1 比例压力阀阀芯的受力分析
比例阀的阀芯受力情况如图3所示,与弹簧的弹性力相比,库仑摩擦力fc很小,为简便计算,fc忽略不计。得到比例压力阀阀芯的受力平衡方程:
(1)
式中,m为阀芯的质量,u为阀的控制电压,p为输出压力,k为反馈弹簧刚度,β为阀芯和阀套之间的粘滞阻尼系数,xv为阀芯的位移,ku为比例系数,SA为膜片截面积。
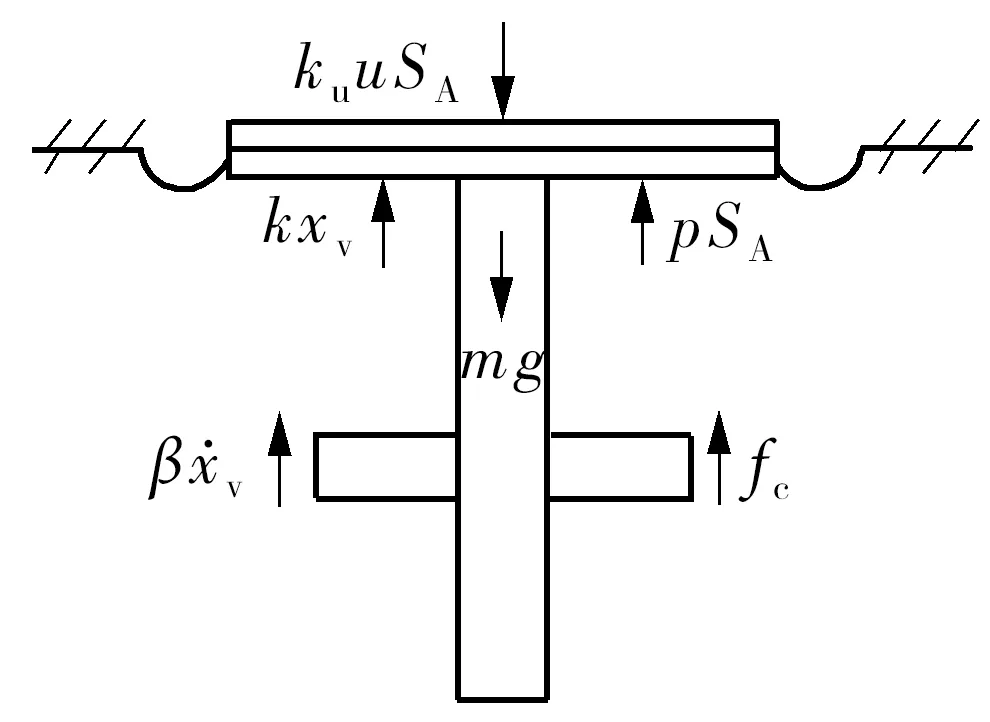
图3 阀芯受力分析图Fig.3 Force analysis diagram of valve spool
1.1.2 比例压力阀的质量流量方程
气体通过阀口的流动近似为理想气体通过收缩喷管的一维等熵流动[14]。当阀的出口压力大于或者小于设定压力时,阀的调节过程不同,下面分别讨论:
(1)当比例阀的出口压力低于设定压力时,阀的进气口打开,进口压力ps即为供气绝对压力,则通过阀口的质量流量为
(2)
(3)
式中,Q为通过阀口的质量流量,C为声速流导,p为输出压力,T为阀口上游绝对温度,b为临界压力比。
(2)当比例阀的出口压力高于设定压力时,阀的排气口打开,排气口压力近似为大气压,则通过阀口的质量流量为
(4)
(5)
式中,pa为阀排气口绝对压力。
1.2 气缸模型
根据能量守恒定律进行简化,得到气缸两腔的压力微分方程:
(6)
式中:R为气体常数;κ为等熵指数,对于空气κ=1.4;V10、V20分别为气缸两腔的起始容积;l为气缸的行程;qm1、qm2分别为进入无杆腔和有杆腔的质量流量。
气缸的受力平衡方程为
(7)
式中,mp为活塞质量,x为气缸活塞的位移,p1、p2分别为无杆腔和有杆腔的压力,S1、S2分别为无杆腔活塞和有杆腔活塞的有效面积,Ff为气缸摩擦力,FL为气缸受到的外负载力。
1.3 摩擦力模型
根据对摩擦力实验现象的观察,选用LuGre摩擦力模型来描述摩擦力的动、静态现象:
(8)
式中,σ0为鬃毛刚度,σ1为微观阻尼,σ2为弹性摩擦系数,v为接触表面之间的相对运动速度,vs为Stribeck速度,Fc为库伦摩擦力,Fs为最大静摩擦力。
由式(1)-(8)即可得到气动阀控缸系统的模型。
摩擦力对气动系统控制性能的影响非常大,为验证所建立的数学模型的正确性,首先需要确定一组摩擦力参数,然后在此参数条件下比较仿真模型和实际系统的一致程度。
在摩擦力模型中,σ0、σ1属于静态摩擦力参数,而σ2、vs、Fc和Fs属于动态摩擦力参数。
(1)动态摩擦力参数的确定
给气缸三角波的位置信号,并改变三角波信号的幅值及频率,使气缸的活塞在不同速度下做匀速直线运动,此时负载的加速度为0,通过采集不同速度时气缸两腔压力信号的大小,即可确定σ2和Fc的大小。
当气缸位置进入稳态后,由于PID控制的积分作用,活塞会克服最大静摩擦力开始围绕设定位移值波动,用此现象来确定Fs的大小。
实验选取5组实验结果的平均值,得到的速度-摩擦力见表1。经在Matlab中拟合后,得到的速度-摩擦力关系如图4所示。

表1 不同方向的速度-摩擦力Table 1 Velocity-friction force under different directions
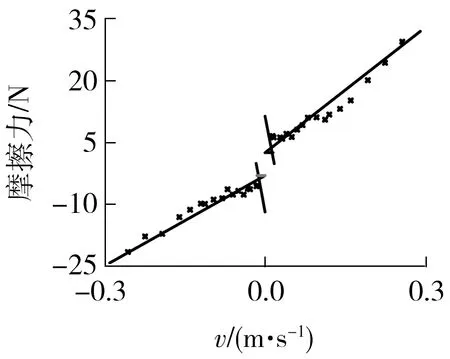
图4 速度-摩擦力关系Fig.4 Relationship between velocity and friction
(2)静态摩擦力参数的确定
由于用三角波位移信号很难测得气缸低速时的摩擦力,可用正弦波信号(如图5所示)补充其低速时的摩擦力。运用最小二乘法对实验数据进行拟合,得到低速时的速度-摩擦力关系见图6。从图中可以看出:当气缸运行速度大于Stribeck速度时,拟合曲线和实验曲线贴合得比较好;当气缸运行速度小于Stribeck速度时,活塞杆缩回方向上的拟合曲线和实验曲线的误差较大,这是由于拟合时以伸出方向的结果为主,但实际中气缸伸出、缩回时所受到的摩擦力不一致。经过对实验结果的拟合,得到静态摩擦力参数鬃毛刚度σ0=100 kN/m,σ1=1 Ns/m。
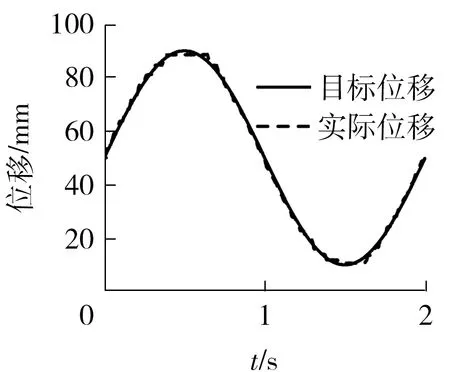
图5 正弦位移信号Fig.5 Sinusoidal displacement signals

图6 低速时的速度-摩擦力关系Fig.6 Relationship between velocity and friction at low speed
2 系统仿真及实验验证
由于并联机构中自由度之间相互耦合的问题不在本文的讨论范围内,文中将单个气动分支作为研究对象,其实验控制回路如图7所示。
实验对象采用SMC公司的ITV1050型电/气比例压力阀、CE1型行程可读气缸(其位置测量精度为±0.2 mm)、ISE30A型压力传感器,NI公司的cRIO-9035控制器。
2.1 在Matlab/Simulink中建立数学模型
为了验证系统的数学模型与实际系统的相符程度,具体的模型参数设置如下:m=0.01 kg,下弹簧刚度k2=550 kN/m,上弹簧刚度k1=50 kN/m,l=0.1 m,β=100 Ns/m,SA=0.000 686 875 m2,ku=60 kPa/V,R=287.1 N·m/(kg·K),κ=1.4,ps=701 300 Pa,Ts=293.15 K,pa=101 300 Pa,mp=0.1 kg,A1=0.000 49 m2,A2=0.000 41 m2,FL=0 N,V10=V20=0.005 m3,气缸摩擦力参数如1.3节所示。在Matlab/Simulink中建立比例压力阀阀控缸模型,并将阀、缸和LuGre摩擦力模型分别封装成子模型,如图8所示。
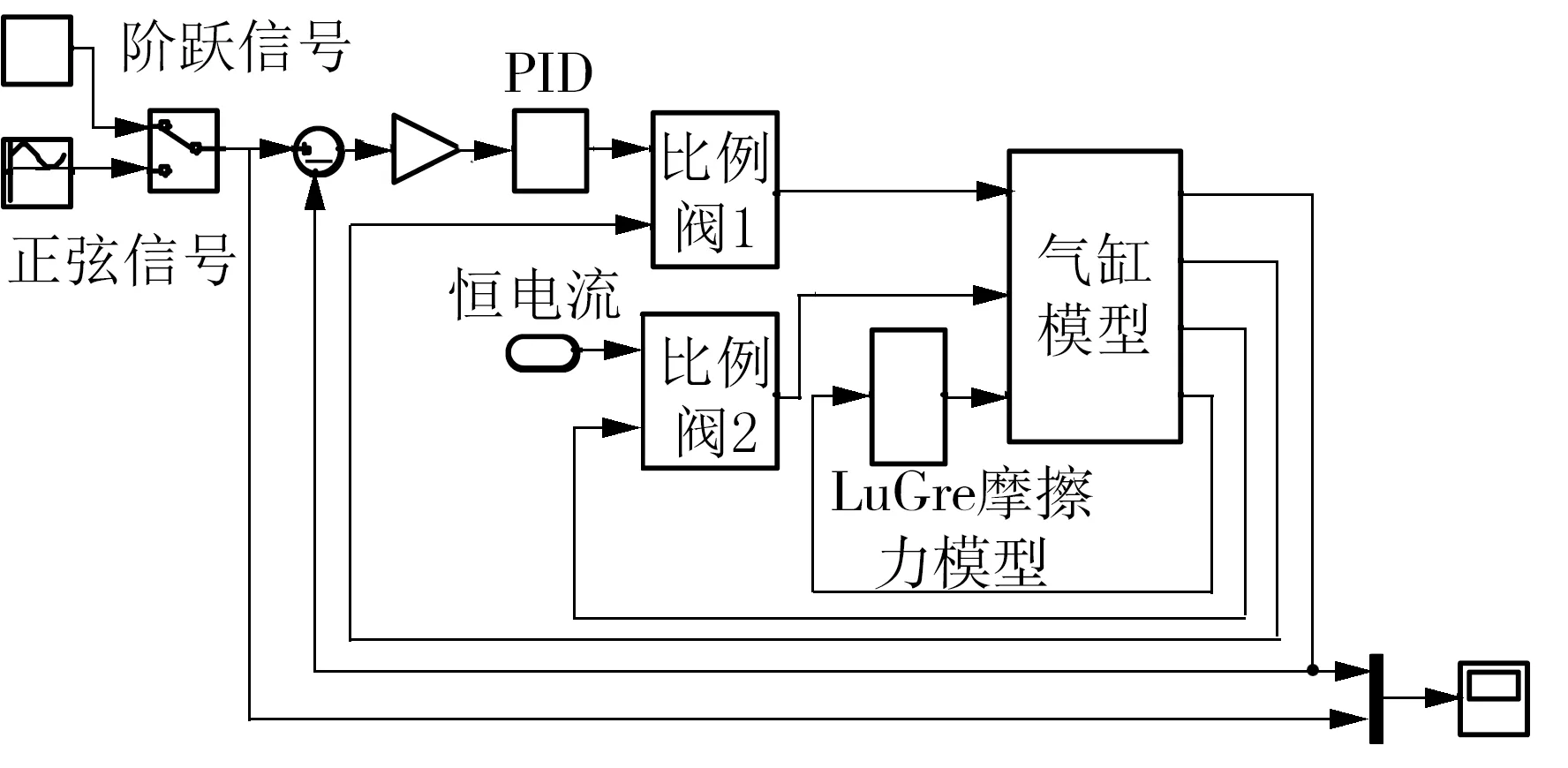
图8 Simulink仿真模型Fig.8 Simulink simulation model
2.2 实验结果对比
取跟随频率为0.1 Hz、幅值为35 mm的正弦位移信号时,其仿真结果与实验结果的对比如图9所示。在正弦信号峰值附近,受摩擦力的影响,气缸活塞停止运动,可以看出,仿真模型能很好地反映出系统跟随正弦位移信号时的动态过程。
将气缸的工作位置选定在中间位置,取幅值为40~45 mm的阶跃位移信号时,其仿真结果与实验结果的对比如图10所示。从图中可以看出,仿真结果可以模拟出气缸活塞迅速达到设定位移时的超调现象,也可以体现出“粘滑振荡”现象,但仿真结果中“粘滑振荡”的振荡频率比实验结果的振荡频率要快,主要有以下几个原因:

图9 正弦位移信号时的仿真和实验结果对比
Fig.9 Comparison between simulated and experimental results of sinusoidal displacement signal
(1)给定阶跃信号时,PID的当前输出有所不同,导致在给定阶跃信号后,气缸无杆腔内的压力变化不同,从而导致活塞表现出不同的运动现象。
(2)摩擦力与温度、气缸位置、润滑情况有关,甚至和运动的历史情况有关。受摩擦力的不确定性影响,导致气缸的运动不具有重复性。
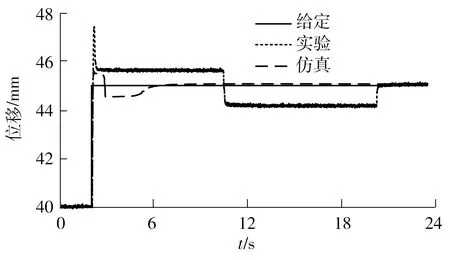
图10 阶跃位移信号Fig.10 Step displacement signals
比较仿真结果和实验结果时发现,系统在跟随阶跃信号时,超调量基本相同,在跟随正弦信号时,响应基本相同,从而验证了文中建立的系统数学模型的正确性,说明所建立的模型有参考价值。
3 有杆腔比例阀叠加高频信号
对于并联系泊机构样机的接舶工况,定位控制尤为重要。但是气缸的摩擦力严重影响了气动控制系统的稳态误差及定位精度。因此,如何克服摩擦力的影响,是提高系统性能的一个重要因素。
3.1 摩擦力补偿原理
孔祥臻等[12]在基于Stribeck摩擦力模型的比例方向阀阀控缸的控制信号中叠加高频低幅的控制信号。而本系统则将高频低幅的高频信号叠加于有杆腔的比例压力阀上,无杆腔比例压力阀的控制信号不受影响,如图11所示,控制起来简单,充分发挥了独立负载口控制的优势。
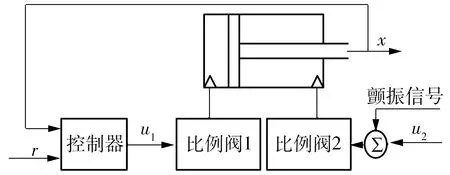
图11 颤振补偿示意图Fig.11 Schematic diagram of chatter compensation
Pervozvanski等[15]基于平均效应理论推导了颤振对系统的影响。图12为叠加颤振信号后的阀控缸运动模型示意图,其运动过程满足方程:
(9)
式中:k为弹性系数;Asin(ωt)为颤振信号,A=aω,ω和A分别为颤振信号的频率和幅值;v0为弹簧端点的恒定速度。

图12 颤振补偿系统模型Fig.12 System model of chatter compensation
经引入无量纲变量、微分形式变换,有
(10)
式中,D(y)为系统运动时所受的附加阻尼,α=a/(mv0),y是一个满足系统运动方程的常数。
从式(10)中可以看出,系统在加入颤振信号后,系统的一部分静摩擦力转变为动摩擦力,减小了系统最大静摩擦力,系统摩擦力主要取决于库仑摩擦力和颤振信号,从而提高系统的定位精度。
3.2 仿真结果分析
在仿真模型中,所有参数保持不变情况下,有、无摩擦力补偿的仿真效果对比如图13所示。从图中可以看出,有杆腔控制信号叠加高频信号后,可以将系统的定位精度从1.0 mm提高到0.5 mm,而且降低了超调的幅值。
当改变仿真模型中高频信号的频率和幅值时,得到的系统误差与频率的关系如图14所示。从图中可以看出:当有杆腔颤振信号频率为10 Hz时,定位效果最好,此频率大约是比例阀的响应频率(9 Hz);当颤振信号的幅值为0.74 N时,定位精度的提高效果不明显;颤振信号幅值为4.12 N时的定位精度不及幅值为1.48 N时的定位精度高,说明颤振信号幅值较小或较大时,摩擦力补偿效果不明显,甚至可能会变差,当颤振信号的幅值接近库伦摩擦力的值时补偿效果最好。

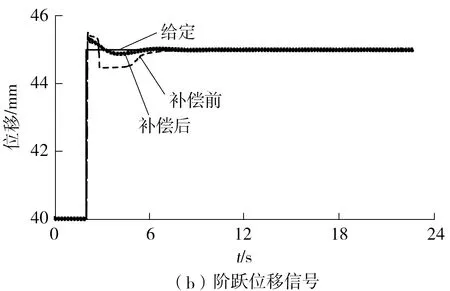
图13 摩擦力补偿前后的仿真结果对比
Fig.13 Comparison of simulation results before and after friction compensation

图14 系统误差与颤振信号频率、幅值的仿真关系
Fig.14 Simulation relationship between system error and frequency,amplitude of chatter signal
3.3 实验结果分析
在所有参数保持不变的情况下,有、无摩擦力补偿的实验结果对比如图15所示。从图中可以看出,有杆腔控制信号叠加高频信号后,可以将系统的定位精度从1.1 mm提高到0.5 mm,而且消除了超调现象,与仿真结果一致。
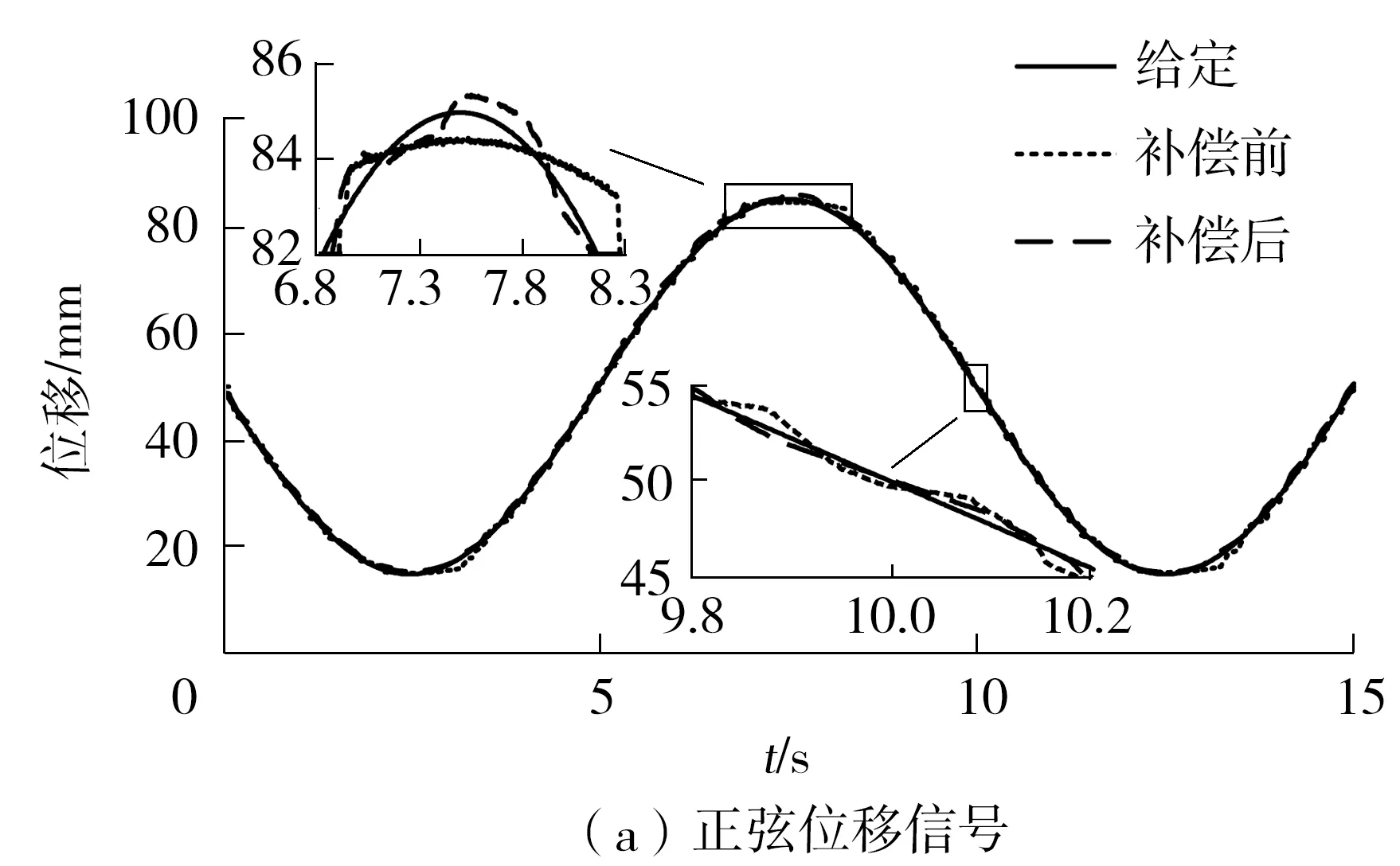
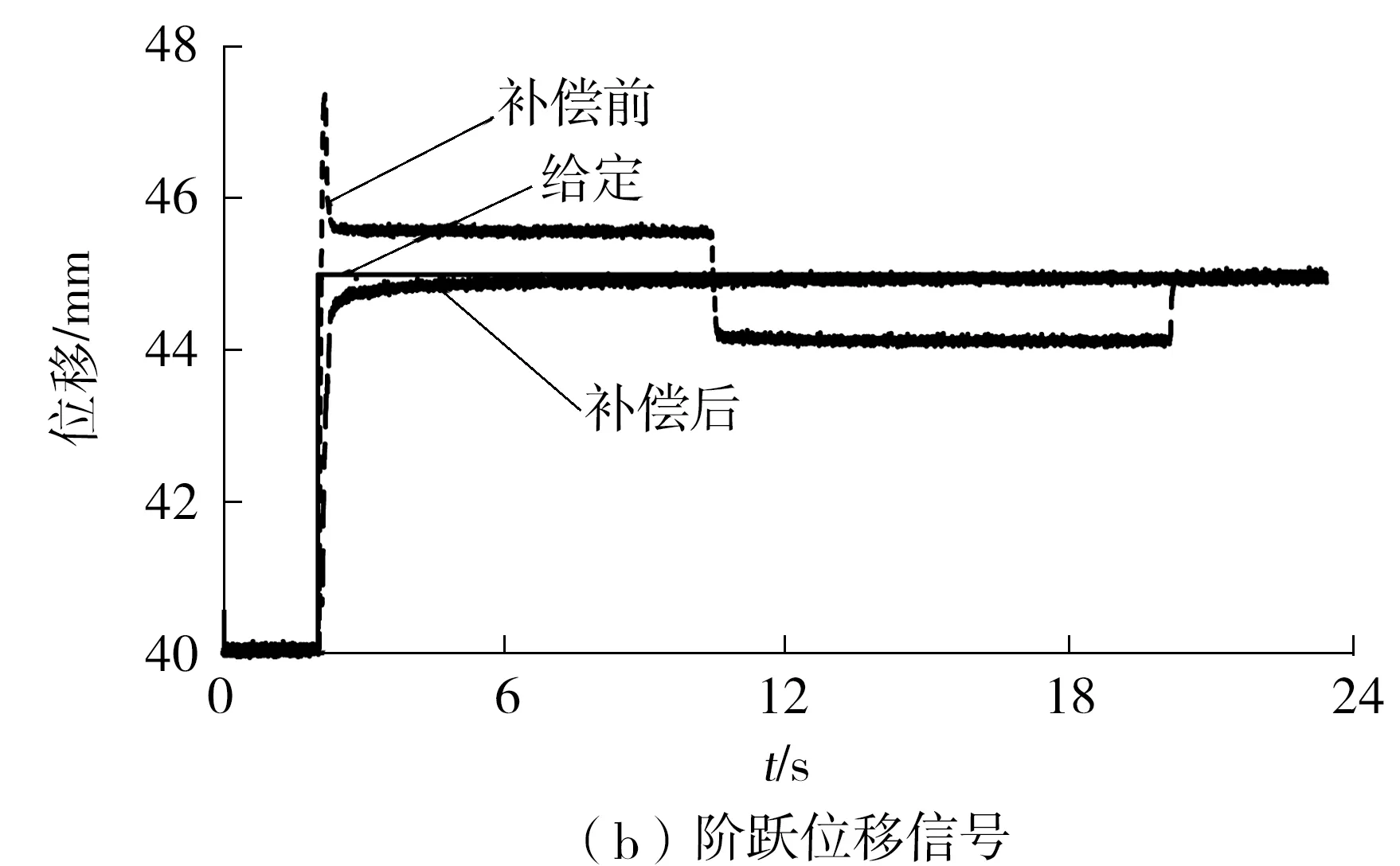
图15 摩擦力补偿前后的实验结果对比
Fig.15 Comparison of experimental results before and after friction compensation
在实验中,改变仿真模型中高频信号的频率和幅值,得到的系统误差与频率的关系如图16所示。从图中可以看出:当有杆腔颤振信号频率为8 Hz时,定位精度最好,此频率相对于比例压力阀的响应频率(9 Hz)稍小;颤振信号的幅值为2.47 N时的定位精度最高,同仿真结果的整体趋势一样,说明颤振信号幅值较小或较大时,摩擦力补偿效果不明显,甚至可能会变差,当颤振信号的幅值接近库仑摩擦力的值时补偿效果最好。
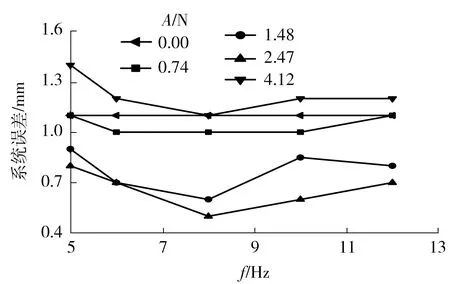
图16 系统误差与颤振信号频率、幅值的实验关系
Fig.16 Experimental relationship between system error and frequency,amplitude of chatter signal
4 结论
(1)文中建立了双比例压力阀阀控缸的动态数学模型,仿真结果与实验结果基本一致,说明了所建立的比例压力阀阀控缸数学模型的正确性与合理性。为建立并联系泊机构整机的数学模型以及其他类似系统特性分析奠定了基础。
(2)针对一腔位移闭环、另外一腔恒压的独立负载口控制方式,文中将高频低幅的颤振信号叠加于恒压腔比例压力阀控制信号,能够有效地抵消部分摩擦力,仿真及实验结果表明,通过对摩擦力进行补偿,可以将系统的定位精度从1.1 mm提高到0.5 mm。
(3)颤振信号的补偿效果与所叠加信号的幅值和频率有关。颤振信号的频率接近比例阀的响应频率时,补偿效果最佳。若颤振信号的幅值过大,会使气缸产生较大的加速度,系统不稳定;若幅值过小,则补偿效果不明显;当颤振信号幅值接近库仑摩擦力值时,补偿效果最好。
