关于一个三元变系数欧拉函数方程的正整数解
2020-03-14张明丽
张明丽, 高 丽
(延安大学数学与计算机科学学院, 陕西 延安 716000)
对于任意的正整数n,Euler函数φ(n)定义为在序列1 , 2 , … ,n-1中与n互素的整数的个数.Euler函数是数论中一个重要的函数,倍受学者们的关注.文献[1]提出了关于它的一些重要性质以及与它相关的不定方程的正整数解问题.在所有的数论函数中,欧拉函数是一类重要的积性函数,即对任意的正整数m,n,当m和n互素时,有φ(mn)=φ(m)φ(n).近期,文献[1-10]分别讨论了当k=2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 11 , 12时,欧拉方程φ(mn)=k(φ(m)+φ(n))的可解性问题;文献[11-13]分别讨论了当k=3 , 4 , 5时,三元欧拉函数方程φ(abc)=k(φ(a)+φ(b)+φ(c))的全部正整数解;对于二元变系数欧拉函数方程φ(ab)=mφ(a)+nφ(b),张四保[14]讨论了当m=5,n=7 时的可解性问题, 白继文[15]讨论了当m=7,n=9 时的可解性问题.本文基于杨张媛[16]的关于三元变系数欧拉函数方程φ(abc)=φ(a)+2φ(b)+3φ(c)的全部正整数解和袁和才[17]的关于三元变系数欧拉函数方程φ(abc)=2φ(a)+3φ(b)+4φ(c)的全部正整数解,以一组较为特殊的勾股数作为系数,研究三元变系欧拉函数方程φ(abc)=3φ(a)+4φ(b)+5φ(c)的可解性问题,利用初等方法给出了该方程的所有40组正整数解.
1 引理
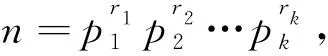
引理2[17]对于任意的正整数m与n,有
其中d=(m,n),表示m与n的最大公约数.
显然,若(m,n)=1,则有
φ(mn)=φ(m)φ(n).
引理3[17]当1≤n≤2时,有φ(n)=1;当n≥3时,有φ(n) 引理4[17]在欧拉函数方程φ(abc)=k+lφ(c)中,若 φ(ab)≥k+l+1, 则该方程无正整数解. 证明因为 (k+1)φ(c)≥k+1, 因此φ(abc)=k+lφ(c)不成立. 定理1三元变系欧拉函数方程 φ(abc)=3φ(a)+4φ(b)+5φ(c) 共有下述40组正整数解: (a,b,c)=(3,8,4),(4,8,3),(3,10,4),(4,10,3),(4,5,4),(4,5,6),(6,5,4),(3,16,3),(3,20,3),(3,15,4),(4,15,3),(7,1,23),(9,1,23),(7,1,46),(7,2,23),(14,1,23),(9,1,46),(9,2,23),(18,1,23),(15,1,12),(39,1,5),(52,1,5),(56,1,5),(35,1,8),(39,1,8),(72,1,5),(45,1,8),(78,1,5),(39,1,10),(39,2,5),(84,1,5),(35,1,12),(7,3,3),(9,3,4),(9,4,3),(7,3,6),(7,6,3),(14,3,3),(19,3,4),(19,4,3). 证明对于欧拉函数方程 φ(abc)=3φ(a)+4φ(b)+5φ(c). (1) 由引理2得 (2) 由引理3有 3φ(a)+4φ(b)+5φ(c)= φ(abc)≥φ(a)φ(b)φ(c), 即 3φ(a)+4φ(b)≥(φ(a)φ(b)-5)φ(c)≥ φ(a)φ(b)-5. 对于上述不等式在φ(a)φ(b)-5<0时的情况进行讨论:当φ(a)φ(b)-5<0时,即φ(a)φ(b)<5,有如下几种情况: 1)当φ(a)=1时,φ(b)=1 , 2 , 4; 2)当φ(a)=2时,φ(b)=1 , 2; 3)当φ(a)=4时,φ(b)=1;经检验此情况不成立(由引理3和引理4可证),故有 (φ(a)-4)(φ(b)-3)≤17. (3) 下面根据φ(a),φ(b)的不同取值分19种情况进行讨论. 情形1:当(φ(a)-4)(φ(b)-3)<0时,则有φ(a)=1 , 2,φ(b)≥4或者φ(a)≥6,φ(b)=1 , 2. Ⅰ 当φ(a)=1,φ(b)≥4时,此时φ(abc)=3+4φ(b)+5φ(c),又由引理3可知,当φ(c)≥2时,φ(abc)为奇数,所以只考虑φ(c)=1的情况,即φ(abc)=8+4φ(b)≥φ(b),此时由不等式推得φ(b)任意,与φ(b)≥4矛盾,故此时式(1)无解. Ⅱ 当φ(a)=2,φ(b)≥4时,有 6+4φ(b)+5φ(c)=φ(abc)≥φ(b)φ(c), 即(φ(b)-5)(φ(c)-4)≤26. 1) 当φ(a)=2,φ(b)=4时,φ(c)任意取值,此时式(1)为: 此时φ(c)-2≤5,即φ(c)=1 , 2 , 4 , 6. 当φ(c)=1时,不存在这样的a,b,c可使得φ(abc)=27,故此时式(1)无解. 当φ(c)=2时,φ(abc)=32,即abc=51,64,68,80,96,102,120,又a=c=3,4,6,b=5,8,10,12,经检验此时式(1)的解为(a,b,c)=(3,8,4),(4,8,3),(3,10,4),(4,10,3),(4,5,4),(4,5,6),(6,5,4). 当φ(c)=4时,φ(abc)=42,即abc=43,49,86,98,又a=3,4,6,b=c=5,8,10,12,经检验此时式(1)无解. 当φ(c)=6时,φ(abc)=52,即abc=53,106,又a=3,4,6,b=5,8,10,12,c=7,9,14,18,经检验此时式(1)无解. 2)当φ(a)=2,φ(b)=6时,此时φ(c)-2≤2,即φ(c)=1,2,4. 当φ(c)=1时,不存在这样的a,b,c可使得φ(abc)=35,故此时式(1)无解. 当φ(c)=2时,φ(abc)=40,即abc=41,55,75,82,88,100,110,132,150,又a=c=3,4,6,b=7,9,14,18,经检验此时式(1)无解. 当φ(c)=4时,不存在这样的a,b,c可使得φ(abc)=50,故此时式(1)无解. 3)当φ(a)=2,φ(b)=8时,此时φ(c)-2≤1,即φ(c)=1,2. 当φ(c)=1时,不存在这样的a,b,c可使得φ(abc)=43,故此时式(1)无解. 当φ(c)=2时,φ(abc)=48,即abc=65,104,105,112,130,140,144,156,168,180,210,又a=c=3,4,6,b=15,16,20,24,30,经检验此时式(1)的解为(a,b,c)=(3,16,3),(3,20,3),(3,15,4),(4,15,3). 4)当φ(a)=2,φ(b)=10时,此时φ(c)-2≤1,即φ(c)=1,2. 当φ(c)=1时,不存在这样的a,b,c可使得φ(abc)=51,故此时式(1)无解. 当φ(c)=2时,φ(abc)=56,即abc=87,116,174,又a=c=3,4,6,b=11,22,经检验此时式(1)无解. 5)当φ(a)=2,φ(b)≥12时,此时φ(c)-2≤0,即φ(c)=1,2. 当φ(a)=2,φ(c)=1时,代入式(1)有φ(abc)=11+4φ(b),即φ(abc)为奇数,故此时式(1)无解. 当φ(a)=2,φ(c)=2时,φ(abc)=16+4φ(b)≥4φ(b),此时可得φ(b)任意,与φ(b)≥12的前提条件矛盾,故此时式(1)无解. Ⅲ 当φ(b)=1,φ(a)≥6时,有 4+3φ(a)+5φ(c)=φ(abc)≥φ(a)φ(c), 即(φ(a)-5)(φ(c)-3)≤19. 1)当φ(b)=1,φ(a)=6时,有22+5φ(c)=φ(abc)≥6φ(c),即φ(c)-3≤19. 当φ(c)=1时,φ(abc)=27,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,φ(abc)=32,即abc=51,64,68,80,96,102,120,又a=7,9,14,18,b=1,2,c=3,4,6,经检验此时式(1)无解. 当φ(c)=4时,φ(abc)=42,即abc=43,49,86,98,又a=7,9,14,18,b=1,2,c=5,8,10,12,经检验此时式(1)无解. 当φ(c)=6时,φ(abc)=52,即abc=53,106,又a=7,9,14,18,b=1,2,c=7,9,14,18,经检验此时式(1)无解. 当φ(c)=8时,不存在这样的a,b,c使得φ(abc)=62,故此时式(1)无解. 当φ(c)=10时,φ(abc)=72,即abc=73,91,95,111,117,135,146,148,152,182,190,216,222,228,234,252,270,又a=7,9,14,18,b=1,2,c=11,22,经检验此时式(1)无解. 当φ(c)=12时,φ(abc)=82,即abc=83,166,a=7,9,14,18,b=1,2,c=13,21,26,28,36,42,故此时式(1)无解. 当φ(c)=16时,φ(abc)=102,即abc=103,206,a=7,9,14,18,b=1,2,c=17,32,34,40,48,60,经检验此时式(1)无解. 当φ(c)=18时,φ(abc)=112,即abc=113,145,226,232,290,348,a=7,9,14,18,b=1,2,c=19,27,38,54,经检验此时式(1)无解. 当φ(c)=20时,不存在这样的a,b,c使得φ(abc)=122,故此时式(1)无解. 当φ(c)=22时,φ(abc)=132,即abc=161,201,207,268,322,402,414,又a=7,9,14,18,b=1,2,c=23,46,经检验此时式(1)有解为(a,b,c)=(7,1,23),(9,1,23),(7,1,46),(7,2,23),(14,1,23),(9,1,46),(9,2,23),(18,1,23). 2)当φ(b)=1,φ(a)=8时,有28+5φ(c)=φ(abc)≥8φ(c),即φ(c)-3≤6. 当φ(c)=1时,φ(abc)=33,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,不存在这样的a,b,c使得φ(abc)=38,故此时式(1)无解. 当φ(c)=4时,φ(abc)=48,即abc=65,104,105,112,130,140,144,156,168,180,210,又a=15,16,20,24,30,b=1,2,c=5,8,10,12,经检验此时式(1)有解为(a,b,c)=(15,1,12). 当φ(c)=6时,φ(abc)=58,即abc=59,118,又a=15,16,20,24,30,b=1,2,c=7,9,14,18,经检验此时式(1)无解. 当φ(c)=8时,不存在这样的a,b,c使得φ(abc)=68,故此时式(1)无解. 3)当φ(b)=1,φ(a)=10时,有34+5φ(c)=φ(abc)≥10φ(c),即φ(c)-3≤3. 当φ(c)=1时,φ(abc)=39,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,φ(abc)=44,即abc=69,92,138,又a=11,22,b=1,2,c=3,4,6,经检验此时式(1)无解. 当φ(c)=4时,φ(abc)=54,即abc=81,162,又a=11,22,b=1,2,c=5,8,10,12,经检验此时式(1)无解. 当φ(c)=6时,φ(abc)=64,即abc=85,128,136,160,170,192,204,240,又a=11,22,b=1,2,c=7,9,14,18,经检验此时式(1)无解. 4)当φ(b)=1,φ(a)=12时,有40+5φ(c)=φ(abc)≥12φ(c),即φ(c)-3≤2. 当φ(c)=1时,φ(abc)=45,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,不存在这样的a,b,c使得φ(abc)=50,故此时式(1)无解. 当φ(c)=4时,φ(abc)=60,即abc=61,77,93,99,122,124,154,186,198,又a=13,21,26,28,36,42,b=1,2,c=5,8,10,12,经检验此时式(1)无解. 5)当φ(b)=1,φ(a)=16时,有52+5φ(c)=φ(abc)≥16φ(c),即φ(c)-3≤1. 当φ(c)=1时,φ(abc)=57,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,不存在在这样的a,b,c使得φ(abc)=62,故此时式(1)无解. 当φ(c)=4时,φ(abc)=72,即abc=73,91,95,111,117,135,146,148,152,182,190,216,222,228,234,252,270,又a=17,32,34,40,48,60,b=1,2,c=5,8,10,12,经检验此时式(1)无解. 6)当φ(b)=1,φ(a)=18时,有58+5φ(c)=φ(abc)≥18φ(c),即φ(c)-3≤1. 当φ(c)=1时,φ(abc)=63,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,不存在这样的a,b,c使得φ(abc)=68,故此时式(1)无解. 当φ(c)=4时,φ(abc)=78,即abc=79,158,又a=19,27,38,54,b=1,2,c=5,8,10,12,经检验此时式(1)无解. 7)当φ(b)=1,φ(a)=20时,有64+5φ(c)=φ(abc)≥20φ(c),即φ(c)-3≤1. 当φ(c)=1时,φ(abc)=69,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,不存在这样的a,b,c使得φ(abc)=74,故此时式(1)无解. 当φ(c)=4时,φ(abc)=84,即abc=129,147,172,196,258,294,又a=25,33,44,50,66,b=1,2,c=5,8,10,12,经检验此时式(1)无解. 8)当φ(b)=1,φ(a)=22时,有70+5φ(c)=φ(abc)≥22φ(c),即φ(c)-3≤1. 当φ(c)=1时,φ(abc)=75,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,φ(abc)=80,即abc=123,164,165,176,200,220,246,264,300,330,又a=23,46,b=1,2,c=3,4,6,经检验此时式(1)无解. 当φ(c)=4时,不存在这样的a,b,c使得φ(abc)=90,故此时式(1)无解. 9)当φ(b)=1,φ(a)=24时,有76+5φ(c)=φ(abc)≥24φ(c),即φ(c)-3≤1. 当φ(c)=1时,φ(abc)=81,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,不存在这样的a,b,c使得φ(abc)=86,故此时式(1)无解. 当φ(c)=4时,φ(abc)=96,即abc=97,119,153,194,195,208,224,238,260,280,288,306,312,336,360,390,420,又a=35,39,45,52,56,70,72,78,84,90,b=1,2,c=5,8,10,12,经检验此时式(1)的解为(a,b,c)=(39,1,5),(52,1,5),(56,1,5),(35,1,8),(39,1,8),(72,1,5),(45,1,8),(78,1,5),(39,1,10),(39,2,5),(84,1,5),(35,1,12). 10)当φ(b)=1,φ(a)≥26时,则φ(c)-3≤0. 当φ(c)=1时,φ(abc)=9+3φ(a),即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,φ(abc)=14+3φ(a)≥2φ(a),经检验此时式(1)无解. Ⅳ 当φ(b)=2,φ(a)≥6时,此时8+3φ(a)+5φ(c)=φ(abc)≥2φ(a)φ(c). 1)当φ(b)=2,φ(a)=6时,有φ(abc)=26+5φ(c)≥12φ(c),即φ(c)-1≤2. 当φ(c)=1时,φ(abc)=31,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,φ(abc)=36,即abc=37,57,63,74,76,108,114,126,又a=7,9,14,18,b=3,4,6,c=3,4,6,经检验此时式(1)的解为(a,b,c)=(7,3,3),(9,3,4),(9,4,3),(7,3,6),(7,6,3),(14,3,3). 2)当φ(b)=2,φ(a)=8时,φ(abc)=32+5φ(c)≥16φ(c),即φ(c)-1≤1. 当φ(c)=1时,φ(abc)=37,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,φ(abc)=42,即abc=43,49,86,98,又a=15,16,20,24,30,b=c=3,4,6,经检验此时式(1)无解. 3)当φ(b)=2,φ(a)=10时,φ(abc)=38+5φ(c)≥20φ(c),即φ(c)-1≤1. 当φ(c)=1时,φ(abc)=43,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,φ(abc)=48,即abc=65,104,105,112,130,140,144,156,168,180,210,又a=11,22,b=c=3,4,6,经检验此时式(1)无解. 4)当φ(b)=2,φ(a)=12时,φ(abc)=44+5φ(c)≥24φ(c),即φ(c)-1≤1. 当φ(c)=1时,φ(abc)=49,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,φ(abc)=54,即abc=81,162,又a=13,21,26,28,36,42,b=c=3,4,6,经检验此时式(1)无解. 5)当φ(b)=2,φ(a)=16时,φ(abc)=56+5φ(c)≥32φ(c),即φ(c)-1≤1. 当φ(c)=1时,φ(abc)=61,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,φ(abc)=66,即abc=67,134,又a=17,32,34,40,48,60,b=c=3,4,6,经检验此时式(1)无解. 6)当φ(b)=2,φ(a)=18时,φ(abc)=62+5φ(c)≥36φ(c),即φ(c)-1≤1. 当φ(c)=1时,φ(abc)=67,即φ(abc)为奇数,故此时式(1)无解. 当φ(c)=2时,φ(abc)=72,即abc=73,91,95,111,117,135,146,148,152,182,190,216,222,228,234,252,270,又a=19,27,38,54,b=c=3,4,6,经检验此时式(1)有解为(a,b,c)=(19,3,4),(19,4,3). 7)当φ(b)=2,φ(a)≥20时,有φ(c)-1≤0. 当φ(c)=1时,φ(abc)=13+3φ(a),即φ(abc)为奇数,故此时式(1)无解. 情形2:当(φ(a)-4)(φ(b)-3)=0时,则有φ(b)=3,φ(a)任意取值,或者φ(a)=4,φ(b)任意取值. Ⅰ由于φ(b)=3(不存在),故此时式(1)无解. Ⅱ当φ(a)=4,φ(b)任意取值时,有φ(abc)=12+4φ(b)+5φ(c)≥4φ(b)φ(c). 当φ(c)=1时,φ(abc)=17+4φ(b),即φ(abc)为奇数,此时式(1)无解. 当φ(c)=2时,φ(abc)=22+4φ(b)≥8φ(b),即φ(b)=1,2,4. 1)当φ(b)=1时,不存在这样的a,b,c可使得φ(abc)=26,故此时式(1)无解. 2)当φ(b)=2时,φ(abc)=30,即abc=31,62,又a=5,8,10,12,b=3,4,6,c=3,4,6,经检验此时式(1)无解. 3)当φ(b)=4时,不存在这样的a,b,c可使得φ(abc)=38,故此时式(1)无解. 4)当φ(b)≥6时,不等式φ(abc)=22+4φ(b)≥8φ(b)推出φ(b)≤4,不存在这样的a,b,c可使得φ(b)≤4与φ(b)≥6同时成立,故此时式(1)无解. 情形3:当(φ(a)-4)(φ(b)-3)=1时,则有φ(a)=5,φ(b)=4;或者φ(a)=3,φ(b)=2,由于φ(a)=3与φ(a)=5(由引理3,上述三种情况均无解,舍去),故此时式(1)无解. 情形4:当(φ(a)-4)(φ(b)-3)=2时,则有φ(a)=6,φ(b)=4;或者φ(a)=5,φ(b)=5(同上,舍去);或者φ(a)=3,φ(b)=1(同上,舍去);或者φ(a)=2,φ(b)=2. 现考虑φ(a)=6,φ(b)=4的情况,则有φ(abc)=34+5φ(c)≥24φ(c),即φ(c)=1.而当φ(c)=1时,φ(abc)=39,即φ(abc)为奇数,故此时式(1)无解. 当φ(a)=2,φ(b)=2时,则有φ(abc)=14+5φ(c)≥4φ(c),即φ(c)任意,经检验此时式(1)无解. 情形5:当(φ(a)-4)(φ(b)-3)=3时,则有φ(a)=7,φ(b)=4(同上,舍去);或者φ(a)=5,φ(b)=6(同上,舍去);或者φ(a)=1,φ(b)=2. 当φ(a)=1,φ(b)=2时,φ(abc)=11+5φ(c),即φ(abc)为奇数,故此时式(1)无解. 情形6:当(φ(a)-4)(φ(b)-3)=4时,则有φ(a)=8,φ(b)=4;或者φ(a)=6,φ(b)=5(同上,舍去);或者φ(a)=5,φ(b)=7(同上,舍去);或者φ(a)=2,φ(b)=1. 现考虑φ(a)=8,φ(b)=4的情况,则有φ(abc)=40+5φ(c)≥32φ(c),即φ(c)=1.而当φ(c)=1时,φ(abc)=45,即φ(abc)为奇数,故此时式(1)无解. 当φ(a)=2,φ(b)=1时,φ(abc)=10+5φ(c)≥2φ(c),即φ(c)任意,经检验此时式(1)无解. 情形7:当(φ(a)-4)(φ(b)-3)=5时,则有φ(a)=9,φ(b)=4(同上,舍去);或者φ(a)=5,φ(b)=8(同上,舍去),故此时式(1)无解. 情形8:当(φ(a)-4)(φ(b)-3)=6时,则有φ(a)=5,φ(b)=9(同上,舍去);或者φ(a)=6,φ(b)=6;或者φ(a)=7,φ(b)=5(同上,舍去);或者φ(a)=10,φ(b)=4;或者φ(a)=1,φ(b)=1. 当φ(a)=6,φ(b)=6时,则有φ(abc)=42+5φ(c)≥36φ(c),即φ(c)=1.而当φ(c)=1时,φ(abc)=47,即φ(abc)为奇数,故此时式(1)无解. 当φ(a)=10,φ(b)=4时,则有φ(abc)=46+5φ(c)≥40φ(c),即φ(c)=1.而当φ(c)=1时,φ(abc)=51,即φ(abc)为奇数,故此时式(1)无解. 当φ(a)=1,φ(b)=1时,φ(abc)为奇数,故此时式(1)无解. 情形9:当(φ(a)-4)(φ(b)-3)=7时,则有φ(a)=11,φ(b)=4(同上,舍去);或者φ(a)=5,φ(b)=10(同上,舍去),故此时式(1)无解. 情形10:当(φ(a)-4)(φ(b)-3)=8时,则有φ(a)=5,φ(b)=11(同上,舍去);或者φ(a)=6,φ(b)=7(同上,舍去);或者φ(a)=8,φ(b)=5(同上,舍去);或者φ(a)=12,φ(b)=4. 当φ(a)=12,φ(b)=4时,则有φ(abc)=52+5φ(c)≥48φ(c),即φ(c)=1.而当φ(c)=1时,φ(abc)=57,即φ(abc)为奇数,故此时式(1)无解. 情形11:当(φ(a)-4)(φ(b)-3)=9时,则有φ(a)=5,φ(b)=12(同上,舍去);或者φ(a)=7,φ(b)=6(同上,舍去);或者φ(a)=13,φ(b)=4(同上,舍去),故此时式(1)无解. 情形12:当(φ(a)-4)(φ(b)-3)=10时,则有φ(a)=5,φ(b)=13(同上,舍去);或者φ(a)=6,φ(b)=8;或者φ(a)=9,φ(b)=5(同上,舍去);或者φ(a)=14,φ(b)=4(由于不存在这样的a使得φ(a)=14,舍去). 当φ(a)=6,φ(b)=8时,则有φ(abc)=50+5φ(c)≥48φ(c),即φ(c)=1.而当φ(c)=1时,φ(abc)=55,即φ(abc)为奇数,故此时式(1)无解. 情形13:当(φ(a)-4)(φ(b)-3)=11时,则有φ(a)=15,φ(b)=4(同上,舍去);或者φ(a)=5,φ(b)=14(由于不存在这样的b使得φ(b)=14,舍去),故此时式(1)无解. 情形14:当(φ(a)-4)(φ(b)-3)=12时,则有φ(a)=5,φ(b)=15(同上,舍去);或者φ(a)=6,φ(b)=9(同上,舍去);或者φ(a)=7,φ(b)=7(同上,舍去);或者φ(a)=8,φ(b)=6;或者φ(a)=10,φ(b)=5(同上,舍去);或者φ(a)=16,φ(b)=4. 当φ(a)=8,φ(b)=6时,则有φ(abc)=48+5φ(c)≥48φ(c),即φ(c)=1.而当φ(c)=1时,φ(abc)=53,即φ(abc)为奇数,故此时式(1)无解. 当φ(a)=16,φ(b)=4时,则有φ(abc)=64+5φ(c)≥64φ(c),即φ(c)=1.而当φ(c)=1时,φ(abc)=69,即φ(abc)为奇数,故此时式(1)无解. 情形15:当(φ(a)-4)(φ(b)-3)=13时,则有φ(a)=5,φ(b)=16(同上,舍去);或者φ(a)=17,φ(b)=4(同上,舍去),故此时式(1)无解. 情形16:当(φ(a)-4)(φ(b)-3)=14时,则有φ(a)=5,φ(b)=17(同上,舍去);或者φ(a)=6,φ(b)=10;或者φ(a)=11,φ(b)=5(同上,舍去);或者φ(a)=18,φ(b)=4. 当φ(a)=6,φ(b)=10时,则有φ(abc)=58+5φ(c)≥60φ(c),即φ(c)=1.而当φ(c)=1时,φ(abc)=63,即φ(abc)为奇数,故此时式(1)无解. 当φ(a)=18,φ(b)=4时,则有φ(abc)=70+5φ(c)≥72φ(c),即φ(c)=1.而当φ(c)=1时,φ(abc)=75,即φ(abc)为奇数,故此时式(1)无解. 情形17:当(φ(a)-4)(φ(b)-3)=15时,则有φ(a)=5,φ(b)=18(同上,舍去);或者φ(a)=7,φ(b)=8(同上,舍去);或者φ(a)=9,φ(b)=6(同上,舍去);或者φ(a)=19,φ(b)=4(同上,舍去),故此时式(1)无解. 情形18:当(φ(a)-4)(φ(b)-3)=16时,则有φ(a)=5,φ(b)=19(同上,舍去);或者φ(a)=6,φ(b)=11(同上,舍去);或者φ(a)=8,φ(b)=7(同上,舍去);或者φ(a)=12,φ(b)=5(同上,舍去);或者φ(a)=20,φ(b)=4. 当φ(a)=20,φ(b)=4时,则有φ(abc)=76+5φ(c)≥80φ(c),即φ(c)=1.而当φ(c)=1时,φ(abc)=81,即φ(abc)为奇数,故此时式(1)无解. 情形19:当(φ(a)-4)(φ(b)-3)=17时,则有φ(a)=5,φ(b)=20(同上,舍去);或者φ(a)=21,φ(b)=4(同上,舍去),故此时式(1)无解.对以上解进行归纳即得本文结论.2 主要结论及其证明
