画图与分析能力并重*—-广州市2019年数学中考压轴题第24题的探索
2020-03-14广东省广州市第五中学
广东省广州市第五中学
广东省广州市海珠区教育发展中心(510220)罗晓斌
著名数学家波利亚在怎样解题表中,提到过:第一步:你必须弄清问题.1.已知是什么? 未知是什么? 要确定未知数,条件是否充分? 2.画张图,将已知标上.3.引入适当的符号.4.把条件的各个部分分开.第二步:找出已知与未知的联系……
其中在“弄清问题”中第二步提到“画张图”,在初中数学的教与学过程中,“画出准确的图”是一个非常重要的解题策略.画图能够将题干中复杂的数量关系更加直观地表示出来,使学生们一目了然,化繁为简,化难为易,方便学生们快速地找到解题思路.因此在初中阶段的数学教学过程中,教师们要引导学生们进行适当的画图训练,让学生们能够准确地作图,培养通过画图解决问题的能力.实际上,学生解题过程中的画图不仅是一种技能,更是一个操作、观察、思考,体现学生数学核心素养的过程.下面以广州市2019年数学中考压轴题第24题为例说明.
1.原题呈现
24.(本小题满分14分)如图11,等 边ΔABC中,AB= 6,点D在BC上,BD= 4.点E为边AC上一动点(不与点C重合),ΔCDE关于DE的轴对称图形为ΔFDE.

图11
(1)当点F在AC上时,求证DF//AB;
(2)设ΔACD的面积为S1,ΔABF的面积为S2,记S=S1-S2,S是否存在最大值? 若存在,求出S的最大值;若不存在,请说明理由;
(3)当B,F,E三点共线时,求AE的长.
2.分析与解决
第(1)问分析本问题是常规问题.先画出正确的图形,如图11(1),由轴对称知∠DFE= ∠C= 60°,而∠A= 60°,所以∠DFE=∠A,所以DF//AB;
评析这道题的证明原理很简单—-同位角相等,两直线平行.学生的难点之处是要画出正确的图形(即图11(1)),而这个图与原图还是有一定的差异.只有平时教学中注重培养学生画出正确的图形的能力,才能顺利的解决这个问题.

图11(1)

图11(2)
第(2)问分析如图11(2),因为ΔACD的面积为S1为固定值,要求S=S1- S2的最大值,即求S2的最小值,即求点F到直线AB的最小值.作FK⊥AB于点K,DH⊥AB于点H,易求得DH= 4 sin 60°=由轴对称知DF=DC= 2,所以点F在以点D为圆心,半径为2的圆上,当点D,F,K三点共线时(即与DH重合时),FK最小,最小值为FK=DH-2=所以S=S1-S2最大值为:
评析本题目完全可以直接设问:求S2的最小值.但是原题这样设问的原因,可能主要是为了增加学生的阅读、分析、理解的难度和转化的难度.这道题的难点在于隐形圆的发现与运用.如果学生不能经过分析发现“点F在以点D为圆心,半径为2的圆上”,那么这道题就无法求出“点F到直线AB的最小值”!这说明了,画出动点的轨迹(即动点运动的轨迹是什么? 或者说动点在什么样的曲线上运动)对于解决这类动点问题非常重要.
第(3)问分析第三问对于学生而言困难的地方至少有两个,第一个是要重新画一个新图形,第二问的含隐形圆的图形对于第(3)问没有帮助,必须重新画出准确的图形,否则会干扰第(3)问的求解;第二个是如何描述三点共线? 对高中学生而言解决三点共线的知识工具多,例如可利用斜率、向量等等.对于初中学生而言,此题的三点共线的本质是∠BFD= 180° -∠DFE= 120°.虽然此题的位置导致学生有畏难心理,但其实是很“漂亮”的问题,思想丰富,方法众多,可利用的知识有相似,勾股定理,角平分定理,等面积法,正弦定理等等.下面主要介绍5 种不同方法.
方法一(作垂线构造直角三角形,利用勾股定理建立方程)如图11(3)法1,由对称知∠CED= ∠BFD,∠CDE=∠DFE= 60°,当点B,E,F三点 共 线 时,∠BFD=108° -∠DFE= 120°,作
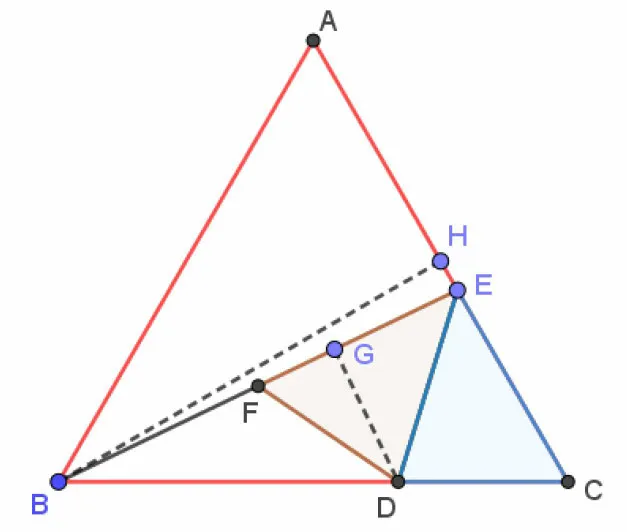
图11(3)法1
在RtΔBGD中,由勾股定理得所以在RtΔBHE中,由勾股定理得BH2+HE2=BE2,即从而
评析方法1 用了三次“解直角三角形”,即在求线段长的时候,如果题目条件中有现成的直角三角形,或者可以通过作垂线得到直角三角形,那么利用勾股定理建立方程就是求线段长的有力工具.对于学生而言难点是“在哪里画垂线,构造什么样的直角三角形”.
除了方法1的构造直角三角形RtΔBHE的方法外,还可以作EM⊥BC,利用Rt∠BEM代替上述的RtΔBHE,其它步骤类似,同样运用勾股定理,也能得到解决.
方法二(作垂线构造直角三角形,利用等面积法建立方程)如图11(3)法2,作DG⊥BE于点G,EM⊥BC于点M,设EC=x,则FE=EC=x,在RtΔFGD中,FD=DC=2,∠DFG=60°,所以FG=1,在RtΔEMC中,EC=x,∠EMC=60°,所以

图11(3)法2
同方法一求得BF=由SΔBEC=SΔBED+ΔDEC,即EM,化简得BC ·EM-DC·EM=BE·DG,即EM ·(BC-DC)=BE·DG,即EM ·BD=BE·DG,这样得到解得从而
方法三(作垂线构造直角三角形,利用相似三角形建立方程)如11(3)法2的图,作DG⊥BE于点G,EM⊥BC于点M,设EC=x,则FE=EC=x,同方法2,先计算出由ΔBGD∽ΔBME(子母型相似),得到即EM ·BD=BE·DG,下面方法同法2.
方法四(利用正弦定理建立方程) 如图11(3) 法4,当点B,E,F三点共线时,∠BFD= 180° -∠DFE=120°, 同 方 法 1 计 算 出设EC=x,则FE=EC=x, 则在ΔBFD中, 由正弦定理得即在ΔBEC中,由正弦定理得即因为sin 120°= sin 60°,上述两式相除,得到方程解得从而
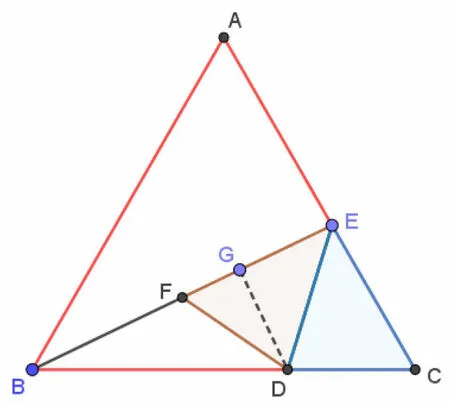
图11(3)法4
评析方法一至方法四,都必须要先求出BF的长,而作高DG,计算BF的长这一过程对于学生而言也是难点,要花费一定的时间.能不能不求BF的长呢?可以!利用角平分定理,即方法五,可能是此题比较简单自然的方法.
方法五(利用角平分线定理和勾股定理建立方程)如图11(3)方法5,由对称知∠CED= ∠BFD,当点B,E,F三点共线时,ED是∠BEC的平分线,由角平分线定理得DG⊥ BE于点G,BH⊥ AC于点H,设EC=x,则FE=EC=x,在RtΔFGD中,FD=DC= 2,∠DFG=60°,所以
设EC=x,则BE=2x,作EG⊥ BC于点G,则在RtΔEGC中,由∠C=60°,所以在 RtΔBGE中,由勾股定理,BG2+GE2=BE2,即解得从而

图11(3)法5
评析方法5 这个角平分线定理用得太妙!避免了去求BF的长,附带轻松的证明了此题中当点F是BE中点时,点B,E,F三点共线.而且可以推广:若题目翻折的条件不变,当点B,E,F三点共线时,若则
3.解题反思与收获
通过分析本题,发现广州市2019年数学中考压轴题第24题对学生的画图能力和分析能力提出了较高的要求.《2018年广州市初中毕业生学业考试年报》也曾指出:要加强学生识图、画图的能力的训练,不仅仅是根据图形能识图解图,还要根据题意画出图像.建议平时的教学中多设计让学生自己画图的题目,让学生有更多的时间和机会亲自动手画图,体会几何图形中所隐含的数量关系和位置关系,增强对图形的观察能力.
画图虽然不能像一把万能钥匙一样解决所有的数学问题,但是可以以一种形象的思维方式将抽象的已知条件过渡成为直观的解题信息,要让画图成为学生们喜爱运用的一种解决问题的有效工具.画图可以有效地培养学生们分析问题的能力,思考问题的能力以及逻辑推理的能力,而这些这是数学核心素养的体现.因此,教师们要以培养初中生们的画图习惯作为一个重要的教学目标,让学生们在画图中有所思,在画图中有多得,使学生们的数学能力得到全面提升,从而提高学生们的数学成绩.当然,在教学过程中教师们要始终把握循序渐进的原则,按照学生们的思维能力和作图能力进行教学,为不同阶段的学生定制不同的教学目标.在初中阶段,对于初一年级的学生,教师们指定的目标可以适当地放低,以加快学生们适立初中数学的学习,可以让学生们读懂线段图,并以线段图为条件列出计算表达式;而对于初二年级的学生就要求必须要根据题目作图,分析题目给出的数量关系,通过作图解决实际应用问题;对于初三年级的学生就要求必须要熟练地运用作图辅助解题,备战中考.实际上,画图解题能力的培养不能仅仅在图上下功夫,更基础的,应该是在学生数学核心概念、原理的学习及问题解决的学习过程中下足功夫,进而全面地提高学生的数学核心素养.
