凹槽结构导致的表面等离激元与波导模式转换特性研究

陈俊学，张斗国

（1.西南科技大学理学院，四川绵阳621010）

（2.中国科学技术大学光学与光学工程系，安徽合肥230026）

表面等离激元（Surface Plasmon Polaritons,SPP）是电磁波与金属表面自由电子耦合而形成的一种沿金属表面传播的近场电磁波。在过去20 年，SPP 以及相关功能器件的研究引起了人们的广泛关注[1-7]。SPP能作为信息载体，可以实现突破衍射极限的光传输。同时，由于SPP高度的空间局域特性，SPP的激发能极大地增强局域电场强度。此外，SPP还对结构表面形貌非常敏感，通过调节表面结构形貌可以控制SPP传播的路径[8-12]。在以前的研究中，通过在金属膜上或者里面制作表面缺陷结构，已经实现了很多SPP的功能器件，如SPP 波导[13-14]、反射镜、棱镜和分束器[15]、SPP光子带隙晶体[16-19]和产生非衍射的SPP光束[20-24]。在这些结构中，金属膜体系中只存在一个表面电磁模式（即SPP 模式）。然而，由于SPP模式具有高的传输损耗和低的共振Q值，这阻碍了SPP在很多方面的实际应用。而波导模式具有低的传输损耗，如果能将SPP和波导模式耦合，就能与其他器件（如源和探测器等）集成。在金属薄膜（如金或银膜）上覆盖一层电介质层，如PMMA或SiO2层，可以构造电介质覆盖的金属波导（Dielectric-coated Metal Waveguide，DMW）。除了SPP模式外，该波导体系还支持波导模式传播。在这个体系中，由于波导模式具有低的传输损耗和对电介质层厚度敏感等特性，波导模式已经被用来实现高效的荧光辐射[25-26]和偏振编码控制的量子非门[27]、引力透镜效应[28]、构造窄的非衍射光束[29]和沿任意路径加速光束传播[29-30]。同时，体系中波导模式也被用来同时实现几何光学的自聚焦效应和波动光学的Talbot 效应[31]。在这些应用中，人们的关注重点是波导模式，而SPP模式被忽略掉了，很少有文献报道在这种介质覆盖金属膜体系中，SPP和波导模式间的相互作用以及结构表面缺陷如何同时影响SPP和波导模式的传播。

在本文中，我们通过在电介质覆盖金属波导的顶层，引入一维亚波长凹槽结构来研究SPP和波导模式间的相互作用。相对于在金属膜上制作凹槽结构（只存在SPP模式），在电介质覆盖金属波导上由于共存有两个电磁模式，凹槽结构将带来更加复杂的光子能带结构。这将为发展二维光子学器件，如光子芯片、耦合器和方向性激发SPP和波导模式提供有效的方案。

1 电介质覆盖金属波导的导波性质

图1（a）中给出了电介质覆盖金属波导的结构示意图。该波导由一厚度为h的SiO2层覆盖在厚度为300 nm 的银膜上组成，整个结构放置在玻璃基底上。在数值模拟中，结构的工作波长为785 nm，材料SiO2、玻璃和银的折射率分别为1.46、1.515和0.033+i5.44[32]。图1（b）给出了模式有效折射率（包括SPP，TM和TE偏振导波模式）随SiO2层厚度的变化关系。从图中可以看出，随着厚度h的减小，导波模式的有效折射率也会随之减小。TM1和TE0模式的截止厚度分别为320 nm 和170 nm。那么通过改变SiO2层的厚度，可以调节导波模式的传播。在本文中，为了比较模式转换效应对SPP和波导模式光子能带的影响，SiO2层的厚度分别固定在160 nm（只支持SPP 模式）和250 nm（同时支持SPP和TE0模式）。在厚度h=250 nm时，SPP和TE0模式的电场分布分别在图1（c）和1（d）中给出。为了简化描述，我们将SPP和TE0模式都命名为结构的导波模式。

图1 （a）电介质覆盖金属波导结构示意图；（b）SPP和波导模式有效折射率随SiO2层厚度h的变化关系；（c）SPP模式对应的归一化的电场分布（Ex和Ez分量）；（d）TE0模式对应的归一化电场分布（Ey分量）

1.1 仅支持SPP模式结构的光子能带

图2（a）给出了电介质覆盖金属波导中模式转换结构的示意图。在SiO2层的表面制作了7个横截面为矩形的凹槽。凹槽的宽度和深度分别表示为wg和hg，相邻凹槽的间距表示为Ld。符号θi、θr和θt分别表示导波模式的入射、反射和透射角度。当导波模式斜入射到凹槽上，该模式除了发生部分反射和透射外，由于凹槽界面的不连续性，导波模式间（SPP模式和TE0模式）的模式转换也会随之发生[33]。通过模式转换，SPP模式可以被TE0模式激发，反之亦然。本文中，导波模式的传输性质通过非周期的严格耦合波分析方法进行研究（Aperiodic Rigorous Coupled-Wave Analysis，ARCWA）[18,34-36]。为了确保结果的收敛性，ARCWA中傅立叶展开阶数取140。当入射波是SPP模式时，Rpp和Tpp分别表示SPP模式的反射率和透射率，Rps和Tps分别表示TE0模式在结构反射端和透射端的产生效率。同样，当入射波是TE0模式时，Rss和Tss分别表示TE0模式的反射率和透射率，Rsp和Tsp分别表示SPP模式在结构反射端和透射端的产生效率。一般来说，模式的转换效率正比于凹槽的深度。然而凹槽越深，导波模式穿过凹槽时，模式的散射损耗也就越大[38]。为了平衡模式的散射损耗与转换效率，本文中，凹槽的宽度和深度分别固定在250 nm和120 nm。如图1（b）所示，当SiO2层的厚度减小为160 nm时，波导结构只支持SPP模式，这种结构是被广泛研究的波导结构，在波导表面制作凹槽结构，可以实现SPP布拉格反射镜。这里，我们先描述凹槽结构实现的SPP光子能带结构。当SPP模式入射到7个凹槽结构时，图2（b）和2（c）分别给出了结构反射率（Rpp）和透射率（Tpp）随入射角和间距Ld的变化关系。由于在凹槽内部和外部，SPP模式具有不同模式的有效折射率，当SPP入射到凹槽上时，与平面波在高低折射率组成的多层膜体系中的传播情况类似，在二维平面上SPP将经历部分反射和透射。当SPP穿过多个凹槽时，由于反射和透射SPP模式间的干涉效应，将形成SPP模式的导带和禁带。

为了比较导波模式和平面波光子能带结构，我们首先了解导波模式和平面波斜入射时偏振行为的差异。图3（a）和3（b）分别给出了导波模式穿过多个凹槽和平面波穿过电介质多层膜时的偏振行为示意图。如图3（a）所示，当TE0模式以角度θi入射到凹槽上时，TE0模式的电场（沿ey′方向）在光波入射面（由入射波矢和界面法线方向决定）内。因此，对比图3（b）可知，当TE0以角度θi入射到凹槽上时，TE0模式将表现出类似于TM偏振平面波的电磁行为。对于SPP模式入射时，SPP模式的电场不仅有垂直于入射面的分量（沿ez′方向），还含有入射面内的分量（沿ex′方向）。由于入射面内重叠的电场分量，当TE0模式和SPP模式斜入射到凹槽时，TE0模式和SPP模式间会发生模式耦合效应，而这个效应在平面波入射到各向同性的电介质多层膜体系中是没有的。从图1（c）中可以看出，SPP模式沿ez′方向的电场分量幅度远大于沿ex′方向的分量。那么，当SPP模式斜入射到凹槽上时，SPP模式将展示类似于TE偏振平面波的电磁行为。对于电介质多层膜体系，TE偏振平面波光子带隙边界在图2（b）和2（c）中以虚线形式表示。电介质多层膜结构中光子能带结构通过以下的布洛赫方程得到[37]：

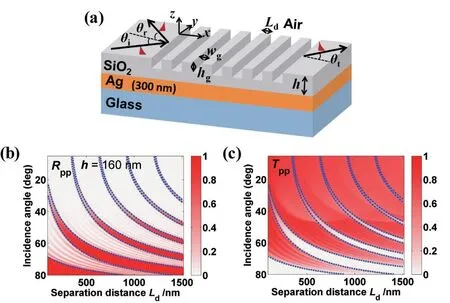
图2 （a）电介质覆盖金属波导中模式转换结构示意图；（b）SPP模式的反射谱；（c）SPP模式的透射谱

图3 导波模式和平面波斜入射时偏振行为的比较。（a）导波模式穿过凹槽结构的示意图；（b）TE和TM偏振平面波斜入射到多层膜结构的示意图

注 多层膜由折射率为n1和n2，厚度为h1和h2的介质层交替组成。TE0模式（电场沿ey′方向）和SPP模式（电场沿ex′和ez′方向）以角度θi入射到凹槽上，neff,1和neff,2分别表示导波模式在凹槽内部和外部的模式有效折射率这里Λ=h1+h2是介质多层膜的周期，h1和h2分别是低折射率（n1）和高折射率（n2）介质层的厚度。γα=，α=1,2，是平面波沿X轴方向的纵向波数；β是平行于Y轴的横向波数；K是多层膜的布洛赫波数。当等式（1）和（2）左边的余弦项的值为1或-1时，可以得到多层膜结构光子带隙的边界[37]。在数值模拟中，为了比较导波模式和平面波的光子能带结构，折射率n1和n2分别取导波模式在凹槽内部和外部的模式有效折射率值。类似的，厚度h1和h2分别等于凹槽宽度wg和间隔距离Ld。如图2（b）和2（c）中所示，在虚线表示的区域内，SPP模式表现出强的反射和低的透射率。这表明，SPP模式在穿过多个凹槽后表现出类似于TE偏振平面波在多层膜中的光子能带结构。

1.2 同时支持SPP和TE0模式结构的光子能带

当SiO2层的厚度增加到250 nm时，结构支持SPP和TE0模式。当入射波是SPP模式时，图4（a）、(b)分别表示SPP模式的反射率（Rpp）和透射率（Tpp）随入射角度和间隔距离Ld的变化情况，其中的虚线表示TE偏振平面波在多层膜中的光子带隙边界。当入射波是TE0模式时，图4（c）和图4（d）分别表示TE0模式的反射率（Rpp）和透射率（Tpp）随入射角度和间隔距离Ld的变化关系，其中的虚线表示TM偏振平面波在多层膜中的光子带隙边界。结构中凹槽的宽度和深度分别为250 nm和120 nm。在图4（a）和（c）中的红色区域表示高反射率；在4（a）和（d）中红色区域表示高透射率。

图5（a）和5（b）分别表示，当SPP模式入射到7个凹槽结构时，在凹槽反射端模式转换效率Rps和凹槽透射端模式转换效率Tps随入射角度和间隔距离Ld的变化关系。由等式（13）和（15）得到的结果在图5中分别以圆形和三角形符号表示。图5（c）、（d）分别表示当入射波为TE0波导模式时，在凹槽反射端模式转换效率Rsp和在凹槽透射端模式转换效率Tsp随入射角度和间隔距离Ld的变化关系。图中红色区域表示强的模式转换效率。

下面将讨论图4（b）和4（d）中低透射带（标记为A和B）的物理起源。当SPP模式入射到凹槽上时，图5（a）和5（b）分别给出了从SPP到TE0模式的模式转换效率随入射角度和间隔距离Ld的变化关系。其中，Rps和Tps分别表示在结构反射端和透射端从SPP模式到TE0模式转换效率。通过比较图4（b）、5（a）和5（b）给出光子能带结构，我们发现，SPP模式透射谱中出现的低透射带A和B（如图4（b）所示)分别归因于TE0模式在结构反射端（Rps，如图5（a）所示）和透射端的激发（Tps，如图5（b）所示）。从图5（a）和5（b）中可以看出，受SPP模式禁带的影响，低透射带A和B会出现不连续的分布。低透射带A和B的位置可以通过反射波和透射波的干涉相长条件获得。在数学上，可以通过广义Fresnel公式来描述导波模式在凹槽间的反射、透射和模式转换[38]。广义Fresnel公式可以通过导波模式在两个凹槽间的反射和透射来得出。

图4 SPP模式的（a）反射率（Rpp）和（b）透射率（Tpp）；TE0模式的(c)反射率（Rss）和（d）透射率（Tss）

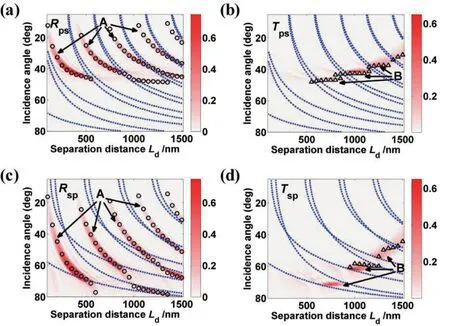
图5 SPP模式入射时，（a）凹槽反射端模式转换效率Rps；（b）凹槽透射端模式转换效率Tps；当入射波为TE0波导模式时，（c）凹槽反射端模式转换效率Rsp；（d）凹槽透射端模式转换效率Tsp

2 模式转换对导波模式光子能带结构的影响

当SiO2层的厚度增加到250 nm 时，结构同时支持SPP 和TE0模式的传播。当SPP 模式入射到凹槽上时，除了部分反射和透射SPP模式外，也会激发起TE0模式。图4（a）和4（b）分别给出了SPP模式反射率和透射率随入射角度和间隔距离Ld的变化关系。类似于图2（b）和2（c）的结果，在虚线表示的范围内，SPP表现出高反射和低透射特性。模拟中，多层膜中折射率n1=1.311 和n2=1.458 分别对应于在凹槽内部和外部SPP模式的有效折射率。此外，在图4（b）中可以看到在SPP的导带中，出现了两个标记为A和B的低透射带。这两个透射带在仅含有SPP模式的结构中没有出现（如图2（c）所示）。这新出现的低透射带来自于SPP和TE0模式间的模式转换。当入射波为TE0模式时，图4（c）和4（d）分别给出了TE0模式的反射率和透射率随入射角度和间隔距离Ld的变化关系。由于斜入射到凹槽上的TE0模式，在偏振特性上表现出类似于TM偏振平面波的特性，在反射谱上可以观察到TE0模式的布儒斯特角效应（如图4（c）所示）。在这个入射角度下，结构的光子禁带宽度为零。从图中可以看出，该结构的布儒斯特角约为38°。与SPP模式的情况类似，在图4（d）中可以看到在TE0模式的导带中，也出现了两个标记为A和B的低透射带。这两个透射带归因于TE0模式到SPP模式间的转换。

2.1 SPP与TE0模式间的模式转换

下面我们引出描述导波模式传输的广义Fresnel公式。在SPP模式入射到两个凹槽结构上时，图6（a）给出了SPP模式的反射率（Rpp）、透射率（Tpp）和模式转换效率（Rps和Tps）随入射角度的变化关系。结构中凹槽间距Ld=400 nm，凹槽的宽度和深度分别为250 nm 和120 nm。为了方便显示，Tps的幅度被放大了5倍。由于凹槽内部和外部SPP模式具有不同的模式有效折射率,当SPP模式穿过凹槽时将经历来回多次反射。反射波间的干涉效应将导致SPP的反射谱和透射谱中出现峰值和低谷。而且，干涉效应也会增强SPP模式的转换效率（Rps和Tps）。图6（b）给出了SPP模式在两个凹槽间的反射、透射和模式转换的简化模型。这里凹槽被认为是一个等价界面。这样含有两个凹槽的结构通过两个等价界面分为3个部分。这3个部分分别标记为0、1和2区域。SPP模式在0区域入射。当SPP模式从i区域到j区域传播时，和分别表示SPP模式的反射和透射系数和分别表示SPP到TE0模式的转换系数。同样的，当TE0模从i区域到j区域传播时，和分别用来表示TE0模式的反射、透射和模式转换系数。对于简化的模型和定义的系数，广义Fresnel 公式可以被用来描述SPP和TE0模式间的模式转换。

当SPP（TE0）模式以幅度（）入射时，SPP和TE0模式在凹槽反射端（和）和透射端（和）的幅度满足如下关系：

图6 SPP模式入射到两个凹槽的结构上时，（a）SPP的反射率（Rpp）、透射率（Tpp）以及模式转换效率（Rps和Tps）随入射角度的变化关系；（b）SPP模式穿过两个凹槽结构时，相应的反射、透射和模式转换的简化模型

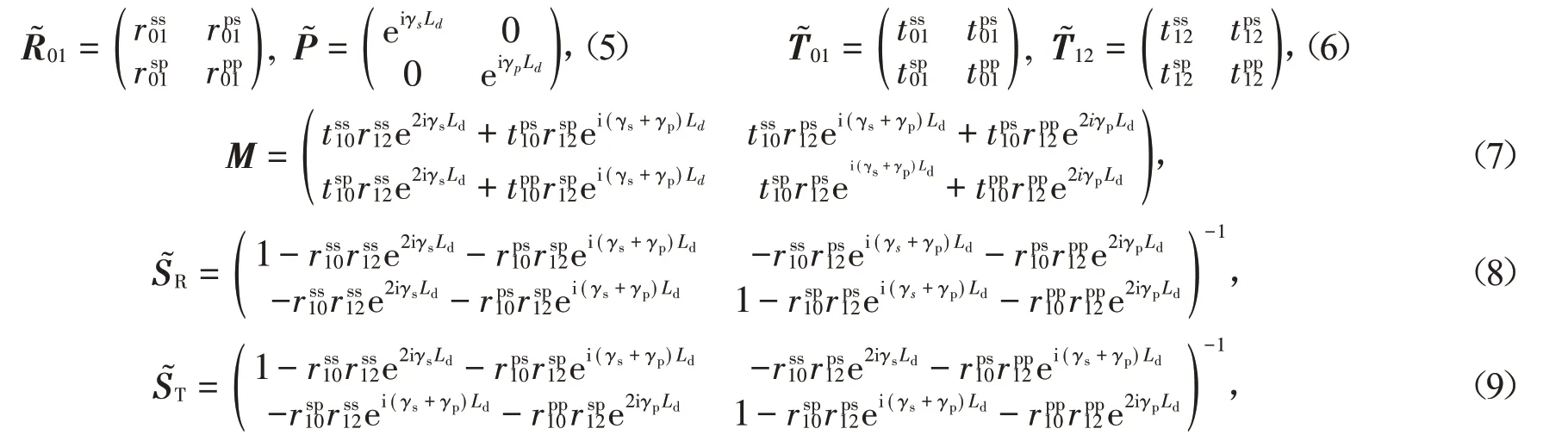
等式（10）的结果在图6（a）中以圆形和三角形符号显示，可以看出Fresnel 公式的结果和通过ARCWA得到的结果符合得很好，说明了Fresnel公式的有效性。此外，当入射波是SPP模式时，从等式（3）和等式（10）中，模式转换系数可以进一步表示为

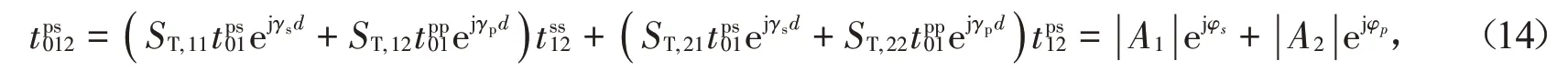
系数ST,ij是矩阵S~T（等式（9））的矩阵元素。等式（14）中同样可以展开为两项。由于两个凹槽间的TE0和SPP模式都能被入射的SPP模式激发，第一项表示凹槽间激发的TE0模式将穿过第二个凹槽在凹槽出射端产生TE0模式的输出。第二项表示激发的SPP模式通过第二个凹槽时，通过模式转换导致的TE0模式输出。这两项的位相分别表示为φs和φp。当这两个位相满足干涉相长时能获得极大值。干涉相长条件表示为

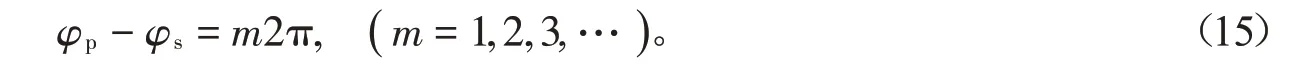
等式（13）和（15）的结果分别在图5（a）和5（b）中以圆形和三角形符号表示，从图中可以看出，Fresnel公式的结果与低透射带（A和B）的变化趋势符合得很好。这意味着，如果我们知道导波模式穿过两个凹槽结构的Fresnel 公式，就能准确预测低透射带A和B的位置。同样，当入射波是TE0模式时，模式转换效率Rsp和Tsp随入射角度和间隔距离Ld的变化关系在图5（c）和5（d）中给出。Fresnel公式决定的干涉相长条件也在图5（c）和5（d）中以圆形和三角形符号给出。

2.2 通过模式转换效应操控SPP和TE0模式的传播

接下来，我们将利用这些新的低透射带A和B来操控二维导波，尤其是通过SPP 和TE0模式间的模式转换实现方向性地二维导波激发。考虑到A和B带（图5中给出）来自于不同的干涉条件，通过改变凹槽间距Ld,SPP模式能被入射的TE0模式高效和方向性地激发，反之亦然。图7（a）和7（b）分别给出了在间距Ld=340 nm 和Ld=1 010 nm时，SPP模式的转换效率Rps和Tps随入射角度的变化关系。当SPP模式的入射角度固定在42.2o时，通过改变间距Ld，TE0模式能在凹槽的反射端或透射端被高效激发。当Ld=340 nm 时，由于干涉相长Rps能获得极大值，而Tps被急剧减小。这意味着，在凹槽结构的反射端TE0模式能被入射的SPP模式高效激发，而在凹槽的透射端，TE0模式的激发是被抑制掉的。在此情况下，图7（c）给出了间距Ld=340 nm 时结构的电场分布。这里，入射的SPP光束被模拟成高斯形状，高斯光束的半高全宽为6λ，λ=785 nm，是入射光的波长。高斯光束的传播是通过角谱分解，然后将每个角谱带入到ARCWA求得。从图7（c）中可以看出，入射的SPP能量在反射端被有效地转换为TE0模式。通过横向动量匹配，可以确定TE0模式的反射和透射角度：

图7 SPP的模式转换效率Rps和Tps随入射角度的变化关系：（a）间距Ld=340 nm，（b）Ld=1 010 nm；SPP模式的入射角固定在42.2o（（a）和（b）中点竖线表示的角度）时，结构在不同间距Ld情况下的电场分布：（c）间距Ld=340 nm，（d）间距Ld=1 010 nm

类似的，当入射波是TE0模式时，图8（a）和8（b）分别给出了在间隔距离Ld=340 nm和Ld=1010 nm时，模式转换效率Rsp和Tsp随入射角度的变化关系。根据光学互易性定理，当TE0模式的入射角度为61.5o，间隔距离Ld=340 nm时，入射的TE0模式能在凹槽的反射端高效地激发SPP模式。当间隔距离Ld增加到1 010 nm时，入射角61.5o附近处的模式转换效率Tsp和Rsp分别被提高和降低。这表明入射的TE0模式在凹槽的透射端有效地激发了SPP模式。在间隔距离Ld=340 nm和Ld=1 010 nm时，结构的电场分布分别在图8（c）和8（d）中给出。从图中可以看出，当间隔距离Ld=340 nm和Ld=1 010 nm时，入射的TE0模式分别在凹槽的反射端和透射端有效激发了SPP模式。根据横向动量匹配，激发的SPP模式的出射角度为42.2o。因此，通过调节凹槽的间隔距离Ld,可以实现SPP和TE0模式的方向性激发。

图8 TE0模式入射时，模式转换效率Rsp和Tsp随入射角度的变化关系：（a）间隔Ld=340 nm，（d）间隔Ld=1 010 nm；TE0模式的入射角固定在61.5°时（（a）和（b）中竖直点线表示的角度），结构在不同间距Ld情况下的电场分布：（c）间距Ld=340 nm，（d）间距Ld=1 010 nm

3 结 论

本文通过在电介质覆盖金属波导中引入一维凹槽结构，理论研究了结构的光子能带特性。由于结构同时支持SPP和TE0模式传播，凹槽结构的引入可以促使两个模式进行耦合转换。模式间的转换导致导波模式的透射谱上出现附加的光子能带。利用这些附加的光子能带，我们实现了通过入射TE0模式高效和方向性地激发SPP模式。同样地，入射的SPP模式也能高效和方向性地激发TE0模式。通过这两个模式的转换可以对二维光波的偏振和场局域特性进行调制，这在分子传感和成像，以及探索二维光波与二维材料作用方面有着潜在的应用。