基于Adams的管道机器人自适应机构优化设计
2020-03-13薛耀勇张继忠王庆前于祥巩健
薛耀勇 张继忠 王庆前 于祥 巩健


摘要: 为了增强履带式管道机器人自适应机构的传力能力,本文优化设计了管道机器人的自适应机构。通过对自适应机构的运动原理进行表述以及对机构进行动力学分析,建立自适应机构的优化设计数学模型。同时,以Adams中參数化建模与优化设计的模块为工具,以对优化目标影响较大的机构参数为优化变量,以机构的结构和运动要求为约束条件,以自适应机构在适应管径过程中对管壁压力最大为目标,对管道机器自适应机构进行优化设计。优化结果表明,优化后自适应机构对管壁压力较优化前提高了11.3%,比较明显的提高了自适应机构传递力的能力,增强了管道机器人爬行能力。该研究为履带式管径自适应管道机器人的后续开发奠定了基础。
关键词: 管道机器人; Adams; 自适应机构; 优化设计
中图分类号: TP241.3 文献标识码: A
收稿日期: 2019-03-08; 修回日期: 2019-06-22
作者简介: 薛耀勇(1992-),男,山东东营人,硕士研究生,主要研究方向为机械设计及理论。
通信作者: 张继忠(1964-),男,教授,主要研究方向为机械系统数字化设计。Email: zjzqdu@163.com
管道广泛应用于石油和天然气等众多工业领域中,而管道机器人作为检测、维护、清洁等管道作业的载体得到广泛应用[1]。履带式机器人能很好地适应管道的变化,具有良好的机动性能,在越障和爬行等方面具有较明显的优势,成为国内、外相关领域研究的重点[2-5]。目前,许多发达国家对各类管道机器人的研究处于领先地位。美国卡内基梅隆大学与美国国家能源部联合研制了ExplorerⅡ,它是以漏磁与视觉双层检测为手段、无缆线、支撑轮式的煤气管道机器人[6];韩国成均馆大学研制开发的MRINSPECT管道机器人,利用支撑机构与双主动万向节使其得以在T型接头与弯头管道中行走[7-8]。近年来,国内许多大学和研究所对多种管道机器人进行研究。唐德威等人[9]通过对机器人在管道内的运动学和动力学进行分析,研发了一种具有自适应功能的管道机器人,在弯管处各行走轮具有良好的功率分配与速度协调能力;施邵宁等人[10]以三轴差速理论为基础,开发设计了一款新型除锈管道机器人;张云伟等人[11]研发了一种利用丝杠螺母进行传动、平行四边形杆系支撑行走轮进行漏磁检测的管道机器人;李鹏等人[12]设计研究了一种螺旋驱动自适应机器人,有效地解决了机器人在越障方面的问题;费振佳等人[13]研制开发了一种履带式管道机器人,并对其进行了动力学仿真分析;王琪等人[14]采用Adams软件中的参数化建模和分析功能,对码垛机器人机构进行优化设计,提高了机构设计效率,缩短了设计周期;焦方坤等人[15]优化设计了一种相贯线埋弧焊接机器人,通过Adams软件进行仿真分析,提高了系统的整体性能;朱华炳等人[16]采用多体动力学分析软件Adams,建立一种工业机器人虚拟样机模型,并进行运动仿真分析,获得机器人末端点运动的位移和速度曲线,为机器人的设计和研究提供了重要依据。机器人结构优化设计能够增强整机性能,提高机构动力传递效率[17-20]。基于此,本文给出了管道机器人自适应机构工作原理,并对机构进行动力学分析,建立自适应机构的优化设计数学模型,同时利用Adams对其进行结构参数的优化设计。该研究为履带式管径自适应管道机器人的后续开发提供了理论基础。
1 自适应机构工作原理及动力学分析
1.1 自适应机构工作原理
为保证机器人能够正常竖直向上爬行,在履带式管道机器人自适应机构适应管道直径变化过程中,需要
管道机器人的履带轮与管道之间具有足够的附着力,履带轮与管道之间的附着力由履带轮与管道内壁之间的正向压力间接决定。本文所述自适应机构,由3组平行四边形支撑杆系,沿管道机器人的中心轴间隔120°均匀分布所组成,而且需要满足Ф210~220 mm管径变化范围及所设计弹簧的要求,自适应机构工作原理如图1所示。
自适应机构主要由以下几部分组成:圆柱螺旋弹簧、同步盘、平行四边形支撑杆系、轴向移动滑块、弹簧预紧套筒等。弹簧预紧套筒与后支撑板固连,同步盘与轴向移动滑块固连。圆柱螺旋弹簧提供的弹簧力,推动轴向移动滑块移动,保证轴向移动滑块及其固连的同步盘沿着机器人的中心轴前、后移动。连接在同步盘上的3个连杆,跟随同步盘移动而推动3组平行四边形支撑杆系运动,使平行四边形支撑杆系能外撑或收缩,并达到适应管径变化的目的。
1.2 动力学分析
为便于研究,本文将自适应机构的3组平行四边形支撑杆系中的其中一组当作研究对象,自适应机构单组支撑杆系受力简图如图2所示。
图2中,支撑杆铰点B和C之间距离为R1,支撑杆铰点A和C之间距离为R2,连杆长度为R3,移动滑块初始水平位移为R4,支撑角α以及连杆的传动角β。连杆受移动滑块水平推力为F,单个履带轮所受牵引力为FZT,法向压力为FN,单个履带轮受管道切向附着力为Ff。其中
Ff=μFN, Ff≥FZT(1)
式中,μ为管道同履带轮间附着系数。在如图2所示的直角坐标系下,自适应机构闭环矢量方程为
R2+R3+R4=h(2)
把以上矢量方程按直角坐标系的x和y坐标轴进行分解,得
R2cos α+R3cos β=R4R2sin α+h=R3sin βα=α0+Δα(3)
式中,α0为支撑杆的起始角度;Δα为自适应机构适应管径变化过程中支撑角的变化量。
适应管径变化是一个非常缓慢的运动过程,自适应机构的力平衡方程为
FAX-F=FZTFAY+Ftan β=FN/2FR2sin(α+β)/cos β+FZTsin α(R1+R2)=FNcos α(R1+R2)/2(4)
综合式(1)~式(4),可以得到自适应机构在正常工作时,每组平行四边形支撑杆系外撑时,对管壁的正压力为
FN=2FR2sin(α+β)cos αcos β(R1+R2)+2FZTtan α(5)
2 建立优化模型
2.1 优化设计变量
分析式(1)~式(5)可知,在自适应管径变化过程中,影响平行四边形支撑杆系外撑力的关键结构参数为:支撑杆铰点B和C之间距离R1,支撑杆铰点A和B之间距离R2,连杆长度R3,初始支撑角α0及初始连杆传动角β0。为减少优化设计过程中设计变量的复杂程度,以铰点A、B、C、D、E、F的坐标为机构设计参数,以铰点B横坐标x1与铰点C横坐标x2为设计变量,即
X=(x1,x2)T(6)
2.2 目标函数
自适应机构在适应管径变化过程中需要保证对管壁压力最大。因此,确定目标函数为
f(X)=max(FN)(7)
2.3 约束条件
自适应机构每组平行四边形支撑杆系可以看作是一个曲柄滑块机构。从已设计的弹簧要求出发,对滑块的移动量ΔR4添加以下约束条件
5.10≤ΔR4≤6.24(8)
从自适应机构的构成条件出发,对铰点B、C的横坐标添加以下约束条件
x2≤x1(9)
从支撑杆刚度出发,自适应机构适应管径变化过程中支撑角α越大越好,但是随着支撑角α的增大,整个管道机器人的径向尺寸就会随之增大,综合考虑对支撑角α和铰点B横坐标添加以下约束
30°≤α≤60°, 17.03≤x1≤51.10(10)
3 Adams優化设计
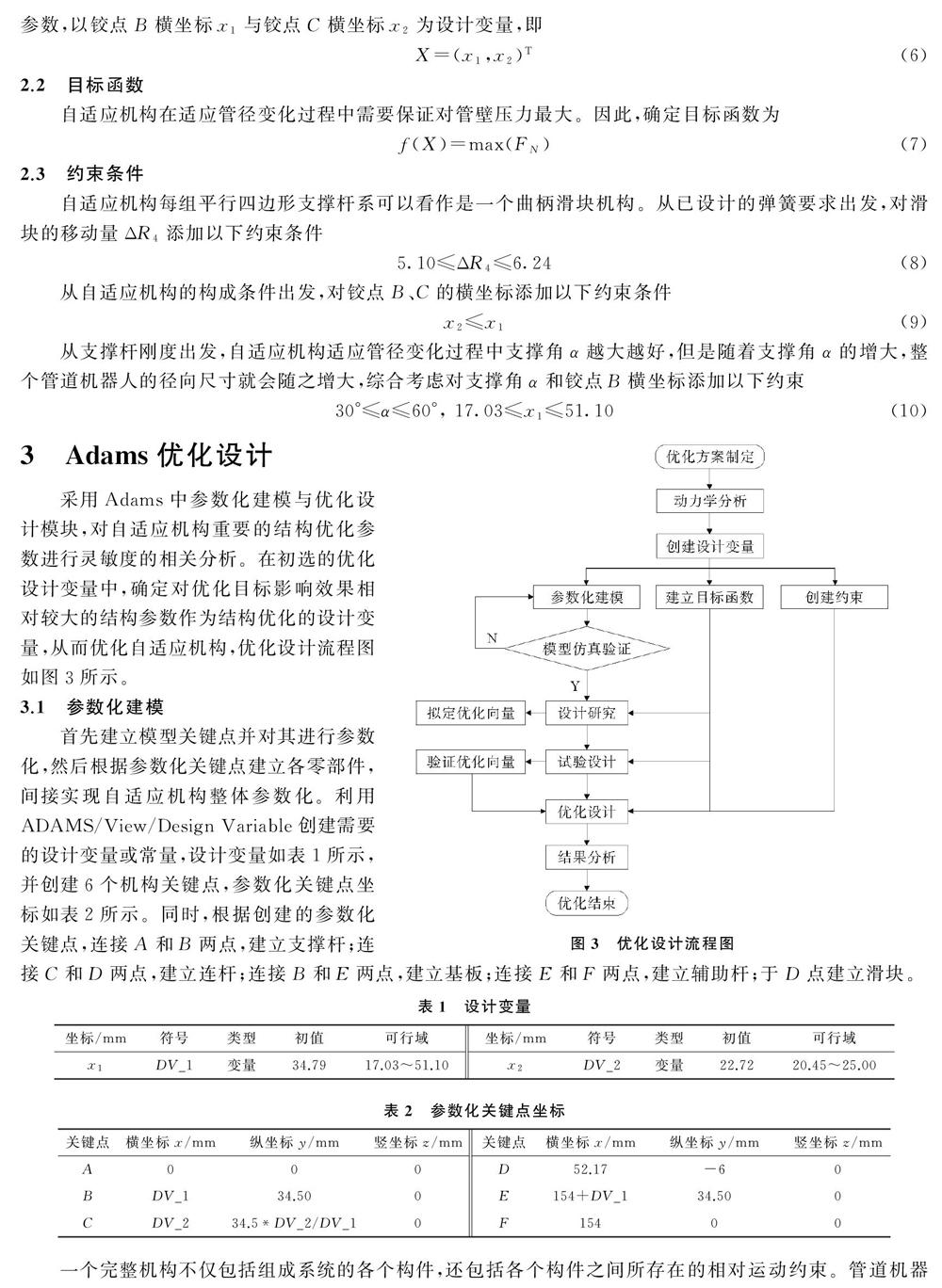
采用Adams中参数化建模与优化设计模块,对自适应机构重要的结构优化参数进行灵敏度的相关分析。在初选的优化设计变量中,确定对优化目标影响效果相对较大的结构参数作为结构优化的设计变量,从而优化自适应机构,优化设计流程图如图3所示。
3.1 参数化建模
首先建立模型关键点并对其进行参数化,然后根据参数化关键点建立各零部件,间接实现自适应机构整体参数化。利用ADAMS/View/Design Variable创建需要的设计变量或常量,设计变量如表1所示,并创建6个机构关键点,参数化关键点坐标如表2所示。同时,根据创建的参数化关键点,连接A和B两点,建立支撑杆;连接C和D两点,建立连杆;连接B和E两点,建立基板;连接E和F两点,建立辅助杆;于D点建立滑块。
一个完整机构不仅包括组成系统的各个构件,还包括各个构件之间所存在的相对运动约束。管道机器人自适应机构模型包括支撑杆、连杆、基板、辅助杆、移动滑块、中心轴等部件,将机架视为地面,通过添加运动副,保证各零部件之间的约束关系。运动副和约束对象如表3所示。
在基板中心施加一个向下速度为10 mm/s的驱动力,模拟自适应机构在适应管径变化过程中受到管壁对于履带轮的正向压力;给滑块中心施加一个水平向左的变力,用以模拟所设计弹簧的弹力,该弹力函数表达式为F=5.65*(.canshuhuayouhua.MARKER_45_MEA_1)-168.4,建立自适应机构参数化优化设计模型,自适应机构参数化模型如图4所示。
采用Adams对自适应机构进行优化设计时,添加约束条件的方式与传统的利用约束方程对设计变量进行约束的方式不同,可直接或间接利用Adams提供的测量工具模块确定,且约束条件的测量函数表达式需要转化为小于等于零的标准形式。通过Bulid/Measure建立约束条件所需要的测量,并通过Build/Measure/Function创建约束条件式(8)~式(10)的标准化测量函数表达式,并通过Simulate/Design constraint利用测量函数对约束条件表达式进行约束。
通过使用Simulate/Design Objective,在Measure选项中选择在基板中心添加的驱动力作为目标函数,适应管径为Ф210 mm~220 mm,仿真过程中的均值作为目标函数在一个优化周期内的取值。
3.2 设计研究
利用Adams中的Design study模块,研究自适应机构参数化模型,在允许范围内变化时,得到各设计变量对自适应机构目标函数的影响特点。自适应机构设计参数灵敏度如表4所示。由表4可知各个设计参数对自适应机构履带轮与管壁之间正向压力FN的灵敏度大小。通过对比发现支撑杆与基板铰点横坐标x1、支撑杆与连杆铰点横坐标x2灵敏度绝对值相差不大,说明这两个参数对自适应机构履带轮与管壁之间正向压力FN影响比较明显,因此优化设计变量无需进行修正(如式(6)所示)。
机器人自适应机构设计如图5所示,由图5可以看出,支撑杆与基板铰点的横坐标x1及支撑杆与连杆铰点的横坐标x2,对自适应机构在适应管径变化过程中向管壁施加正向压力的性能均有较大影响,且后者影响稍大一些。
图5a是以支撑杆与基板铰点横坐标x1为设计变量,以自适应机构适应管径变化过程中履带轮对管壁正向压力FN为目标的设计研究结果。由图5a可以看出,履带轮对管壁正向压力FN随支撑杆与基板铰点横坐标x1呈非线性增大;图5b是以支撑杆与连杆铰点横坐标x2为设计变量,以自适应机构适应管径变化过程中履带轮对管壁正向压力FN为目标的设计研究结果。由图5b可以看出,履带轮对管壁正向压力FN随支撑杆与连杆铰点横坐标x2呈非线性减小。
3.3 优化设计
将支撑杆与基板铰点横坐标x1及支撑杆与连杆铰点横坐标x2作为优化设计变量,在表1要求的变量范围内,在式(8)~式(10)的约束条件限制情况下,以自适应机构适应管径变化过程中履带轮对管壁正向压力FN最大为优化目标,采用Adams中的优化设计功能模块,对自适应机构进行优化设计分析。在自适应机构适应管径变化过程中,履带轮对管壁正向压力FN优化轨迹如图6所示,自适应机构优化前、后对比结果如表5所示。
4 结束语
本文采用了Adams参数化建模与优化设计方法,实现了对履带式管道机器人自适应机构的优化設计。仿真结果表明,与传统的利用编写复杂程序进行优化设计的方法不同,该研究实现了自适应机构在适应管径变化的过程中,履带轮对管壁正向压力较优化前提高11.3%,具有比较明显的优化效果,提高了管道机器人在已设计弹簧驱动下自适应机构传递力的性能,增强了管道机器人的爬行能力,为本课题后续的履带式管径自适应管道机器人的研究奠定了基础。
参考文献:
[1] 王殿君, 李润平, 黄光明. 管道机器人的研究进展[J]. 机床与液压, 2008, 36(4): 185-187.
[2] 曹建树, 林立, 李杨, 等. 油气管道机器人技术研发进展[J]. 油气储运, 2013, 32(1): 1-7.
[3] 刘清友, 李雨佳, 任涛, 等. 主动螺旋驱动式管道机器人[J]. 机器人, 2014(6): 711-718.
[4] 张建伟, 齐咏生, 王林. 一种新型可变径管道机器人的结构设计与控制实现[J]. 测控技术, 2014, 33(10): 64-67.
[5] 杜云, 隋博, 孟凡华, 等. 自动避障三轮管道机器人设计[J]. 河北科技大学学报, 2014, 35(5): 447-453.
[6] Schempf H, Mutschler E, Gavaert A, et al. Visual and nondestructiveevaluation inspection of live gas mains using the explorerTMfamily of pipe robots[J]. Journal of Field Robotics, 2010, 27(3): 217-249.
[7] Choi H R, Ryew S M. Robotic system with active steeringcapability for internal inspection of urban gas pipelines[J]. Mechatronics, 2002, 12(5): 713-736.
[8] Ryew S M, Choi H R. Double active universal joint (DAUJ): Robotic joint mechanism for humanlike motions[J]. IEEE Transactions on Robotics and Automation, 2001, 17(3): 290-300.
[9] 唐德威, 梁涛, 姜生元, 等. 机械自适应管道机器人的机构原理与仿真分析[J]. 机器人, 2008, 30(1): 29-33.
[10] 施绍宁, 赵永强, 王旭飞. 新型管道除锈机行走部的设计与仿真分析[J]. 机械设计与研究, 2010, 26(2): 21-24.
[11] 張云伟, 颜国正, 丁国清, 等. 煤气管道机器人管径适应调整机构分析[J]. 上海交通大学学报, 2005, 39(6): 950-954, 959.
[12] 李鹏, 马书根, 李斌, 等. 具有自适应能力管道机器人的设计与运动分析[J]. 机械工程学报, 2009, 45(1): 154-161.
[13] 费振佳, 张继忠, 张磊, 等. 履带式管道机器人设计及仿真研究[J]. 青岛大学学报: 工程技术版, 2016, 31(2): 37-42.
[14] 王琪, 曹飞, 张任, 等. 基于ADAMS的码垛机器人参数化分析[J]. 组合机床与自动化加工技术, 2014(7): 45-48.
[15] 焦方坤, 汪苏, 李晓辉. 一种相贯线埋弧焊接机器人的结构优化设计[J]. 机床与液压, 2014, 42(21): 36-41.
[16] 朱华炳, 张娟, 宋孝炳. 基于ADAMS的工业机器人运动学分析和仿真[J]. 机械设计与制造, 2013(5): 204-206.
[17] 童超, 侯宇, 阮龙欢, 等. 变形六轮腿式机器人越障性能分析与结构优化设计[J]. 机械设计与制造, 2016(12): 9-12.
[18] 胡伟, 许勇, 张善平. 基于ADAMS的六足机器人腿机构优化设计与仿真[J]. 机械制造, 2014, 52(10): 11-14.
[19] 郑义, 周淑芳, 邓传云. 关节式爬管机器人夹紧机构的优化研究[J]. 机电工程, 2015, 32(3): 328-332.
[20] 任立敏, 谭益松, 殷国成. 具有柔性传动能力的气压驱动微型管道机器人[J]. 液压与气动, 2016(8): 18-23.
Optimization Design of Pipeline Robot Adaptive Mechanism Based on Adams
XUE Yaoyong, ZHANG Jizhong, WANG Qingqian, YU Xiang, GONG Jian
(School of Electromechanic Engineering, Qingdao University, Qingdao 266071, China)
Abstract: In order to enhance the transmission capacity of selfadaptive mechanism of crawler pipeline robot, this paper optimizes the adaptive mechanism of pipeline robot. According to the principle of adaptive mechanism for the presentation and dynamic analysis of institutions, it establishes selfadaptive optimization design mathematical model. It provides optimization design with Adams parameterized modeling and optimized design module as a tool to optimize the goals of the larger institutional parameters for the optimization variables, and with the structure and movement requirements of the organization as a constraint condition, and with adaptive agencies in the process of adapting to the pipe diameter to optimize the pressure on the pipe wall. The optimization results show that the optimized adaptive mechanism improves the pressure of the pipe wall by 11.3%, which obviously improves the transmission ability of the adaptive mechanism and enhances the crawling ability of the pipe robot. The research lays the foundation for the followup development of crawler pipe diameter adaptive pipeline robot.
Key words: pipeline robot; ADAMS; adaptive mechanism; optimization design
