基于Marc的O形圈抗挤出性能分析
2020-03-13陆云江乐2代昌浩
陆云江, 黄 乐2, 代昌浩
(1.苏州工业园区职业技术学院, 江苏苏州 215123; 2.广州机械科学研究院有限公司,广东广州 510535)
引言
O形圈从1939年首次成为专利至今已有80年的历史,由于其结构简单,密封性能好,安装简便,且成本低廉,使其成为一种典型的动、静密封结构,被广泛应用于液压、气动密封系统中[1-4]。
随着计算机仿真技术的发展,已有很多学者借助仿真工具开展了O形圈密封性能的仿真研究[5],如欧阳小平等[6]通过ANSYS软件从材料失效的角度研究了压缩率对O形圈疲劳寿命的影响;黄国冠[7]借助ANSYS软件研究了氟塑料包覆硅橡胶O形圈性能;张毅等[8]利用ANSYS软件分析了深海液压动力源O形圈密封性能;赵斌等[9]利用ANSYS软件研究了磁性橡胶O形圈的密封特性;王伟等[10]借助Marc软件分析了O形圈接触变形及应力分布规律。但这些研究主要还是以O形圈的接触压力和内部应力为主,很少有学者开展O形圈的抗挤出性能仿真研究,这是由于挤出仿真非常容易造成网格畸形,使得计算无法收敛,得不到计算结果。O形圈挤出是指O形圈由于介质压力较大被挤入沟槽间隙的现象,挤出会造成O形圈“咬边”,使密封系统发生泄漏,影响使用寿命,Marc软件的自适应网格重划分技术的出现可以较好的解决收敛问题,为抗挤出性能的有限元分析提供可能。
本研究通过非线性有限元分析软件Marc 建立了O形圈二维轴对称模型,借助其自适应网格重划分技术开展O形圈抗挤出性能分析,研究材料硬度、介质压力、沟槽间隙、初始压缩率、截面直径对其挤出长度的影响规律,并拟合经验公式,以期为O形圈的设计选型提供参考。
1 基于Marc的仿真模型
借助CAD软件建立O形圈的二维轴对称模型,其中O形圈沟槽的槽棱圆角为0.2 mm(尺寸参照GB/T 3452.3),然后导入到Marc软件中,通过四边形网格,采用82号单元进行网格划分,划分后的模型如图1所示。O形圈材料为橡胶材料,通常选用近似不可压缩的两参数Mooney-Rivlin模型进行定义[11-13],Mooney-Rivlin模型的C1,C2参数通过材料硬度由经验公式确定,O形圈的安装沟槽则定义成刚体,无需给定材料属性。
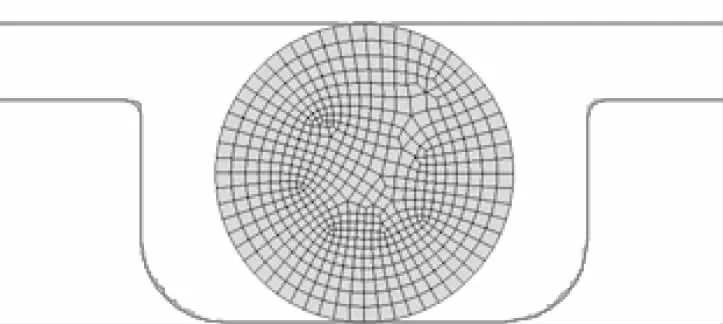
图1 有限元分析模型
通过2个载荷步来模拟O形圈工作状态,第1个载荷步模拟O形圈预安装状态,通过给活塞施加1个径向位移来实现,位移大小依据O形圈的实际压缩率来确定。第2个载荷步模拟O形圈承受介质压力时的承压状态,通过给O形圈的承压面施加1个均布压力来实现,压力大小依据O形圈的实际工作压力来确定,由于介质压力增大到一定程度后O形圈会被挤入沟槽间隙里面,使得O形圈的网格变形后质量得不到保证,通过网格重划分,可以改善网格质量,从而提高模型的收敛性。
2 影响因素分析
以规格φ80×3.55 mm、IRHD硬度为75、介质压力为16 MPa、沟槽间隙为0.2 mm、压缩率为20%的O形圈为研究对象,采用控制变量法通过Marc软件研究单因素作用下材料硬度、介质压力、沟槽间隙、初始压缩率、截面直径分别对O形圈抗挤出性能的影响。其中O形圈的抗挤出性能通过挤出长度L来定义,O形圈挤出长度是指O形圈挤入沟槽间隙t的长度值,挤出长度L值越大说明抗挤出性能越差;材料硬度是指国际硬度IRHD值;介质压力是指O形圈承受的流体压力p;截面直径是指O形圈自由状态下横截面的直径d。初始压缩率ε的计算公式见式(1),各相关尺寸如图2所示。
(1)

图2 相关尺寸定义
2.1 材料硬度影响
其他影响因素不变的情况下,分析5种材料IRHD硬度(65,70,75,80,85)对O形圈抗挤出性能的影响, IRHD硬度与Mooney-Rivlin模型参数的关系为[14]:
lgE=0.0198·Hr-0.5432
(2)
E=6·C1·(1+C2/C1)
(3)
C2/C1=0.05
(4)
式中,Hr为橡胶材料IRHD硬度;E为弹性模量;C1和C2为Mooney-Rivlin系数,各硬度下的Mooney-Rivlin系数换算结果如表1所示。

表1 各硬度下的Mooney-Rivlin系数换算结果
不同材料硬度下O形圈抗挤出性能的有限元分析结果如图3和图4所示,从分析结果可以看出挤出长度随着材料硬度的增加呈下降趋势,挤出长度从最大0.291 mm下降到0.086 mm。

图3 挤出长度随材料硬度变化计算结果
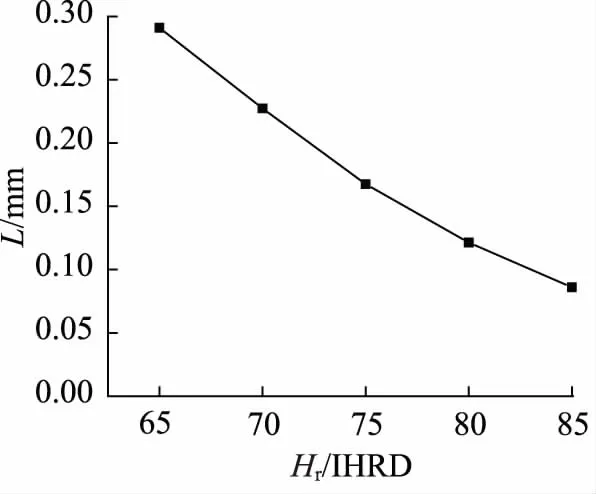
图4 挤出长度随材料硬度变化趋势
2.2 介质压力影响
其他影响因素不变的情况下,分析5种介质压力(8, 12, 16, 20, 24 MPa)对O形圈抗挤出性能的影响,有限元分析结果如图5和图6所示,从分析结果可以看出挤出长度随着介质压力的增大而增加,挤出长度从最小0.048 mm增加到0.271 mm。

图5 挤出长度随介质压力变化计算结果
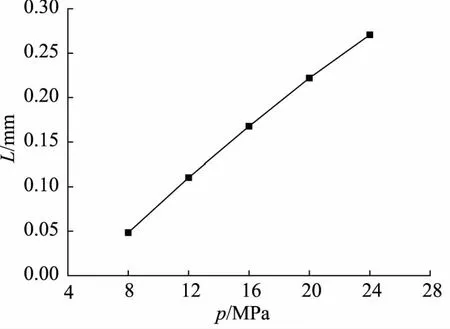
图6 挤出长度随介质压力变化趋势
2.3 沟槽间隙影响
其他影响因素不变的情况下,分析5种沟槽间隙(0.1, 0.15, 0.2, 0.25, 0.3 mm)对O形圈抗挤出性能的影响,有限元分析结果如图7和图8所示,从分析结果可以看出挤出长度随着沟槽间隙的增大而增加,挤出长度从最小0.102 mm增加到0.258 mm。

图7 挤出长度随沟槽间隙变化计算结果
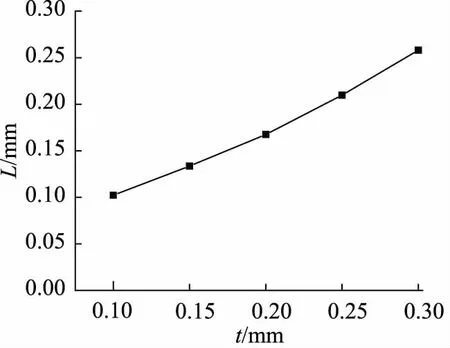
图8 挤出长度随沟槽间隙变化趋势
2.4 初始压缩率影响
其他影响因素不变的情况下,分析5种初始压缩率(12%,16%,20%,24%,28%)对O形圈抗挤出性能的影响,有限元分析结果如图9和图10所示,从分析结果可以看出挤出长度随着压缩率的增大几乎没有变化,可见初始压缩率对O形圈的抗挤出性能几乎没有影响,挤出长度最小为0.166 mm,最大为0.168 mm,变化很小。

图9 挤出长度随压缩率变化计算结果
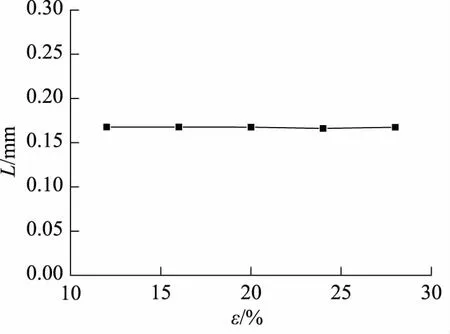
图10 挤出长度随压缩率变化趋势
2.5 截面直径影响
其他影响因素不变的情况下,分析5种国标截面直径(1.8, 2.65, 3.55, 5.3, 7 mm)对O形圈抗挤出性能的影响,有限元分析结果如图11和图12所示,从分析结果可以看出挤出长度随着截面直径的增大呈下降趋势,挤出长度从最大0.220 mm减小到0.126 mm。
3 分析结果处理
从上述的单因素分析结果可知,材料硬度、介质压力、沟槽间隙、截面直径对O形圈抗挤出性能的影响较为显著,因此可以忽略初始压缩率的影响,只考虑挤出长度与上述4个因素的关系。同时为了兼顾数据的全局性,在上述已有数据的基础上,结合正交试验设计方法,参考4因素3水平L9(34)正交设计表,补充了部分分析数据,补充数据如表2所示。

图11 挤出长度随截面直径变化计算结果

图12 挤出长度随截面直径变化趋势
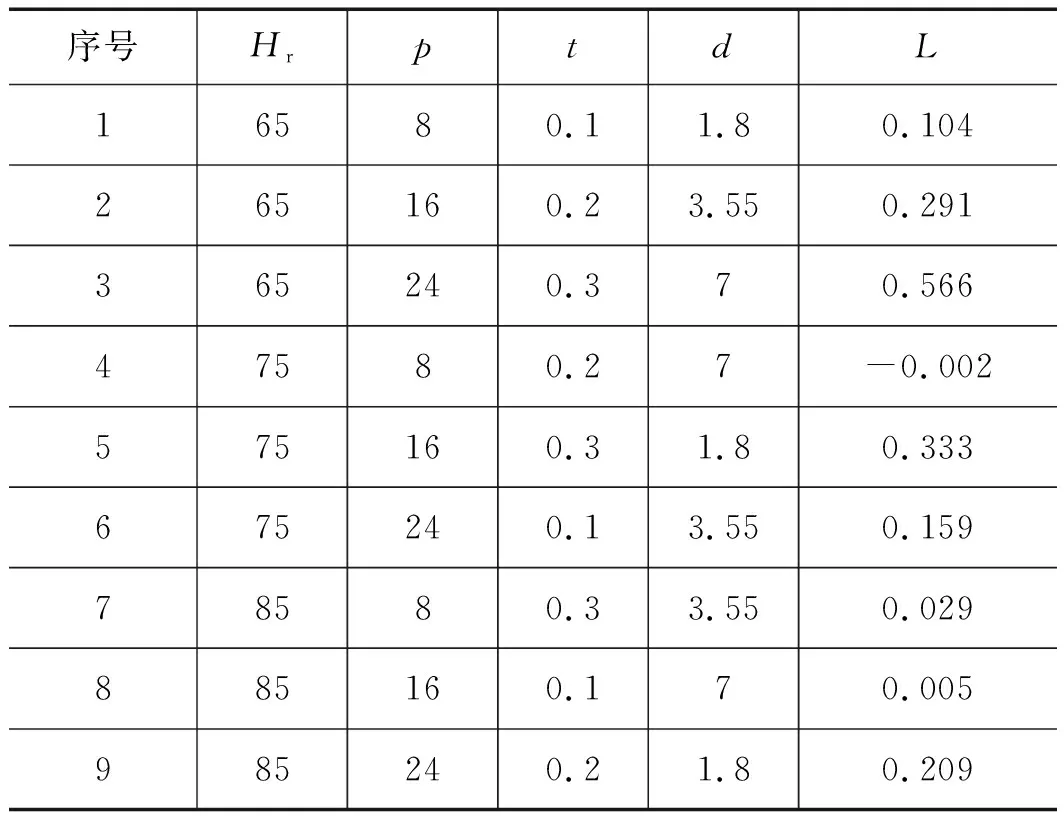
表2 L9(34)正交试验结果
注:负值表示未发生挤出,数值代表与沟槽间隙的距离。
基于上述所有的数据,借助Excel软件的“数据分析”功能对数据进行多元回归分析,同时从上述的单因素分析可知挤出长度L与材料硬度Hr、介质压力p、沟槽间隙t近似呈线性关系,而与截面直径d近似呈二次非线性关系,由于Excel软件不能处理非线性回归问题,因此需要对数据进行线性转换处理,增加一项截面直径的平方项,从而变成五元一次线性回归模型。通过回归分析,相关系数R2为0.9786,说明系数之间高度正相关,显著水平P值为5.07E-15,远小于显著性水平0.05,所以说该回归方程回归效果显著,回归得到的函数关系如式(4)所示。
L=0.709-0.0115·Hr+0.0159·p+1.00·t-
0.057·d+0.0055·d2
(5)
图13给出了原始数据与式(5)计算结果的差异,通过图13也可以看出由式(5)可以估算特定工况下的O形圈的抗挤出性能,计算结果误差较小可以为O形圈的设计选型提供参考。例如,通过计算发现某O形圈的设计方案会发生挤出,则可要求此O形圈需配备挡圈使用,或者对原设计方案进行调整(如提高胶料硬度、减小沟槽间隙等)。
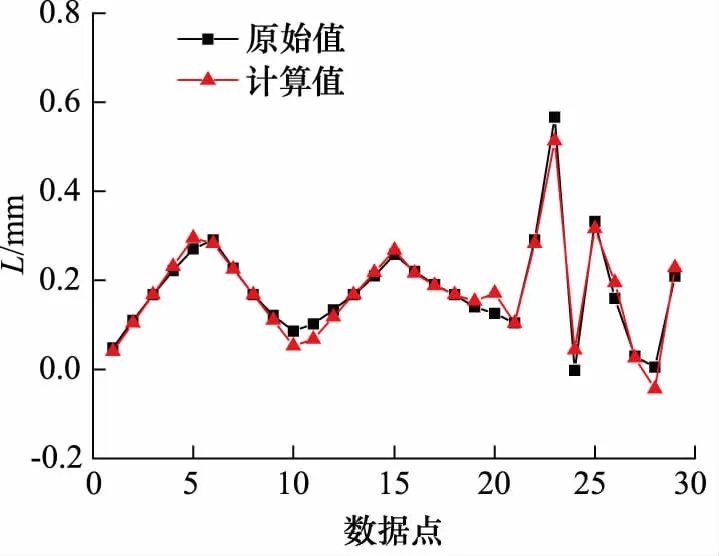
图13 回归结果对比
4 结论
(1) Marc自适应网格重划分技术可以很好的适用于橡胶密封件挤出问题分析,分析过程中模型收敛性好,能够实现不同条件下橡胶密封件的抗挤出性能分析;
(2) 通过控制变量法分析发现O形圈的抗挤出能力随着材料硬度、截面直径的增大而增加,随着介质压力、沟槽间隙的增大而减小,与初始压缩率关系不大;
(3) 借助Excel软件的“数据分析”功能对分析数据进行多元回归分析,得到了挤出长度与各影响因素间的函数关系式(5),通过式(5)可以估算O形圈不同设计方案的抗挤出性能。
