上软下硬复合地层盾构隧洞开挖面稳定性研究

闫军涛， 胡 潇， 刘 波

(1. 河北工程大学水利水电学院, 河北 邯郸 056038; 2. 天津大学 水利工程仿真与国家安全重点实验室， 天津 300072; 3. 河北工程大学土木工程学院, 河北 邯郸 056038)

0 引言

随着地下空间的大规模开发，隧洞工程中遇到的地质条件逐渐复杂化。隧洞盾构掘进过程中，开挖面支护压力的大小对掌子面稳定有重要影响，因支护压力控制不当造成的工程事故时有发生。

国内外许多学者通过各种方式研究了盾构隧洞开挖面支护力计算方法，取得诸多研究成果。村山氏等基于二维试验、施工塌方状况和太沙基松动土压力理论提出二维村山公式，该公式可用于计算楔形体模型最小支护压力[1-2]。G. Mollon等[3]为确定开挖面临界坍塌压力，基于极限分析理论，提出了新的二维破坏机制。P. Chambon等[4]基于黏性土地质条件，通过离心模型试验研究了盾构隧道开挖面稳定性问题。Horn基于筒仓理论和极限平衡法，提出了三维楔形模型[5]。雷明锋等[6]基于坡度因素对盾构隧道极限支护力的影响，利用极限平衡法和仓筒理论，推导了迎坡条件下的开挖面极限支护力计算公式。程诚等[7]在仓筒理论和三维楔形体计算模型的基础上，推导了干砂地层条件下开挖面极限支护力计算公式。周舒威等[8]基于极限平衡理论，研究了大直径顶管开挖面极限支护力问题。Anagnostou等[9]基于楔形体模型并考虑土拱效应，给出了支护压力简单计算公式。吕玺琳等[10]基于村山氏极限平衡法和极限分析上限法研究了盾构隧道开挖面的稳定问题。黄阜等[11]基于极限分析上限定理和空间离散技术，得到了孔隙水压力条件下盾构隧道支护力上限解。陈孟乔等[12]研究了盾构隧道开挖面失稳土体破坏位置。任宏等[13]研究了隧道失稳时的破坏模式，并建立了松动土压力极限分析模型，分析过程中考虑了黏聚力、地表超载等因素。朱建明等[14]将极限支护力计算公式通过线性拟合简化为砂土内摩擦角的线性公式 。黄正荣等[15]采用数值模拟方法研究发现： 盾构隧道开挖面极限支护压力和地下水位关系较大。陈强[16]采用数值模拟方法研究了上软下硬地层条件下盾构隧道开挖面支护压力和破坏模式。赵明华等[17]基于极限平衡理论和筒仓理论，建立了适用于上软下硬地层的盾构隧洞开挖面极限支护力模型，但计算中并未考虑隧洞开挖面孔隙水压力的作用。闫军涛等[18]研究了上软下硬地层条件下盾构隧洞开挖面极限支护力，并分析了开挖面前方地表沉降隆起规律。

上述研究大多未考虑孔隙水压力对开挖面极限支护力的影响。魏纲等[19]提出的梯形楔形体模型比较适用于开挖面为单一土层的情况，对上软下硬地层的适用性有待进一步研究。本文在前人研究的基础上，采用提出的部分梯形楔形体模型计算上软下硬地层条件下隧洞开挖面支护力最小值，计算过程较为简便，最后将模型计算结果与数值模拟结果进行对比。计算方法以期为类似工程极限支护力的确定提供参考。

1 上覆土压力与孔隙水压力

1.1 Terzaghi松动土压力理论

隧洞开挖面上覆土压力的确定是隧洞开挖面极限支护力计算的一项重要内容。太沙基松动土压力理论在计算盾构隧洞上覆土压力中较为常用，其考虑的因素较为全面，例如埋深、土体黏聚力、隧洞尺寸和内摩擦角。

盾构隧洞在开挖过程中，隧洞顶部土体因受到自重作用，顶部土体会有向下滑移的趋势。因此，从隧洞的两侧一定距离到地表会形成2个竖直剪切面。盾构隧洞施工中，土体不可避免地会受到一定程度的施工扰动，竖直剪切面中间土体向下滑动时，滑动与未滑动土体颗粒之间会有相互错动趋势并发生应力传递作用，未滑动的土体会对隧洞上方向下滑动的土体产生一定的阻力。因此，太沙基松动土压力会小于土体原始应力。

采用太沙基松动土压力理论[20]计算圆形隧洞时，竖直滑动土体宽度为2B1，其中：

(1)

式中：R为隧洞半径，m；φ为土的内摩擦角，(°)。

当隧洞上覆土体为多层时，Terzaghi松动土压力如图1所示。

2B1为土体宽度，p0为地面超载，Z为土层厚度，σv为上覆土压力。

图1太沙基松动土压力示意(多层土)

Fig. 1 Terzaghi loose earth pressure diagram(multi-layer)

隧洞顶部土层1处的土压力

(2)

同理可得各个土层之间的相互作用力为：

(3)

(4)

(5)

式(2)—(5)中：p0为地面超载；pi为第i层土与第i+1层土之间的相互作用力；γi为第i层土的重度，kN/m3；ci为第i层土的黏聚力，kPa；φi为第i层土的内摩擦角，(°)；K为侧向土压力系数；Zi为第i层土的土层厚度，m。

1.2 三维松动土压力理论

盾构施工过程中，隧洞开挖面前方土体会形成一个三维松动区，楔形体上部土体在重力作用下有向下滑动趋势，形成柱状松动区[21]。

图2 三维松动土压力示意

微体竖直方向受力平衡：

2B2l1σv+2B2l1γdz=2B2l1(σv+dσv)+2(2B2+l1)cdz+

2(2B2+l1)Kσvtanφdz。

(6)

解此微分方程得：

(7)

式(6)—(7)中：z为土层厚度，m；c为土体黏聚力，kPa。

对于复合地质条件，按照式(7)分土层叠加计算。

1.3 隧洞开挖面中心处孔隙水压力

孔隙水压力是指在颗粒或孔隙之间起作用的土壤或岩石中的地下水压力。水体是盾构隧洞开挖中经常遇到的状况，在施工过程中广泛参与了周围土体的应力重分配。盾构隧洞开挖面极限支护力计算中，孔隙水压力在极限支护力中占有较大比重，忽略孔隙水压力是工程事故发生的重要因素，隧洞开挖面处的孔隙水压力[22]

(8)

式中：ξi为第i层土的土层水压力比率；γw为水重度；hw为水深；B和l分别为隧洞等效直径和滑动楔形体的高度。

2 开挖面破坏形式分析

2.1 计算模型

内摩擦角、泊松比等对上软下硬土(岩)层盾构隧洞开挖面破坏模式影响不大，故本节重点研究弹性模量对盾构隧洞开挖面破坏形式的影响。研究中采用控制变量法，以更好地反应上下土(岩)层弹性模量差异性对开挖面破坏模式的影响。

三维有限元模型如图3所示。模型x轴方向为盾构掘进方向，长30 m；y轴方向与掘进方向垂直，宽30 m；z轴方向为竖向，高20 m。xyz三向符合右手定则，单元类型为C3D4单元，共30 554个，土体采用Mohr-Coulomb本构，管片采用弹性本构。假设隧道直径d=6 m，模型分为上下2层，下层为较硬土层(强风化花岗岩)，上部土(岩)层参数除弹性模量外其余参数与下层一致，2层土(岩)的厚度分别为10 m，开挖面处上软土层与下硬土层层厚比为1，管片厚度为0.3 m。模型底部采用xyz三向约束，x、y方向采用轴向约束，土体顶部为自由表面。计算参数见表1。

图3 三维有限元模型

表1 土层参数

2.2 计算结果分析

以隧洞开挖面土(岩)体y方向(U2方向)位移为判据， 研究开挖面上下土(岩)体弹性模量大小对盾构隧洞开挖面破坏形式的影响。为便于描述，引入弹性模量比的概念，即上下土(岩)层的弹性模量之比，计算中保持下部土(岩)层参数不变，上部土(岩)层取弹性模量比分别为0.1、0.2、0.3、0.4、0.5 时的弹性模量，监测隧洞开挖面中轴线y方向位移的大小。弹性模量比为0.3、0.4时的y方向位移云图如图4和图5所示。计算结果表明： 随着弹性模量比的减小，隧洞开挖面土体y方向最大位移有逐渐向上移动的趋势，但当弹性模量比为0.3时(见图4)，土(岩)体y方向最大位移出现了较大上移。因此，认为当弹性模量比小于0.3时，开挖面为部分破坏，即上部较软土(岩)体部分破坏。

图4 U2方向位移云图(弹性模量比0.3)(单位： m)

Fig. 4 U2 directional displacement chart when elastic modulus ratio is 0.3 (unit: m)

图5 U2方向位移云图(弹性模量比0.4)(单位： m)

Fig. 5 U2 directional displacement chart when elastic modulus ratio is 0.4 (unit: m)

3 对楔形体模型的改进

3.1 部分楔形体模型

前人通过理论研究与物理试验相结合的方式，研究了盾构隧道开挖面破坏模式，提出了楔形体模型。之后不断有学者对楔形体模型进行改进，使得楔形体模型的计算结果越来越接近工程实测和离心试验结果。本小节在前人研究成果基础上，以实际工程为计算背景，基于三维部分楔形体模型(见图6)，计算了考虑孔隙水压力条件下的上软下硬地层隧洞开挖面极限支护力。

图6 部分楔形体模型[16]

3.2 魏纲等修正后的楔形体模型

由于盾构隧洞为圆形，开挖面前方存在拱效应，开挖面前方土体滑动块并不是三角形楔形体。试验表明： 当开挖面前方土体中存在拱效应时，失稳时的滑动块是楔形截柱体，则滑动块上部土柱为梯形棱柱体。魏纲等[19]根据上述理论对楔形体模型进行了改进，提出了梯形楔形体模型(见图7)，并根据梯形滑动块极限失稳状态时受力平衡，推导出开挖面最小支护压力计算式。为验证提出模型的正确性，文献[19]基于工程实例，将模型计算结果与离心试验结果进行了对比。

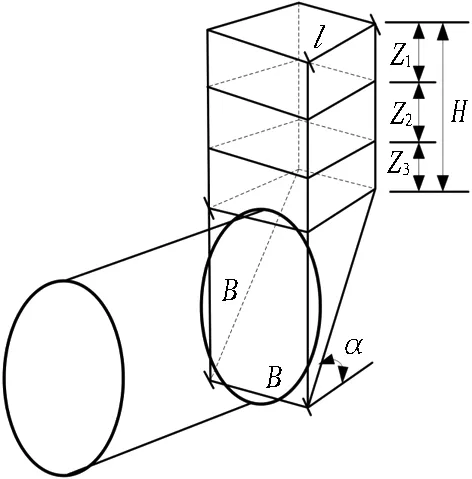
图7 梯形楔形体计算模型[19]

3.3 部分梯形楔形体模型

当盾构隧洞中开挖面前方为单一土层时，开挖面前方土体破坏形式为整体破坏；当开挖面前方为上软下硬复合土层时，开挖面前方土体破坏形式通常为上部较软土体局部破坏。因此，梯形楔形体模型在上软下硬地层中的适用性尚需进一步研究。本小节基于盾构隧洞开挖面上软下硬地质条件，提出了考虑孔隙水压力条件下的部分梯形楔形体模型(见图8)，模型由梯形棱柱体和梯形滑动块组成(见图9)。

图8 部分梯形楔形体模型(本文)

图9 梯形楔形体形状

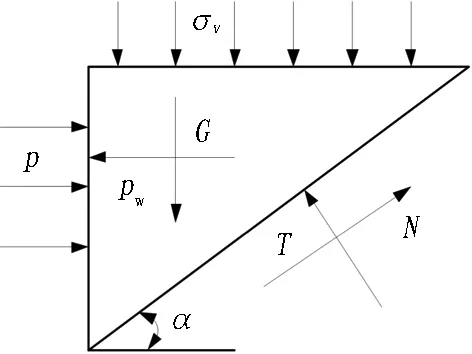
图10 梯形楔形体受力

当梯形滑动块处于极限平衡状态时，由水平方向受力平衡可知

p+Tcosα=Nsinα+pw。

(9)

由竖直方向受力平衡可知

pv+G=Ncosα+Tsinα。

(10)

由Mohr-Coulomb强度理论推得

(11)

联立式(9)—(11)，得最小支护压力

(12)

当隧洞开挖面上的支护压力为矩形时，开挖中心的支护压力

(13)

4 工程实例与分析

4.1 工程概况

某核电工程位于广东省，排水隧洞是工程的难点之一。排水隧洞盾构段SSK1+450～+500区段土(岩)层自上而下分别为淤泥、淤泥质土、粉质黏土、细砂、中粗砂、强风化花岗岩、微风化花岗岩等，地质条件极为复杂。隧洞直径7.4 m，轴线埋深约18.4 m，水深18 m。盾构所穿地层如图11所示，开挖面上部为中粗砂，下部为强风化花岗岩，上下岩土体刚度差异较大，极限支护力控制难度大。土层参数见表2。

图11 盾构穿越地层

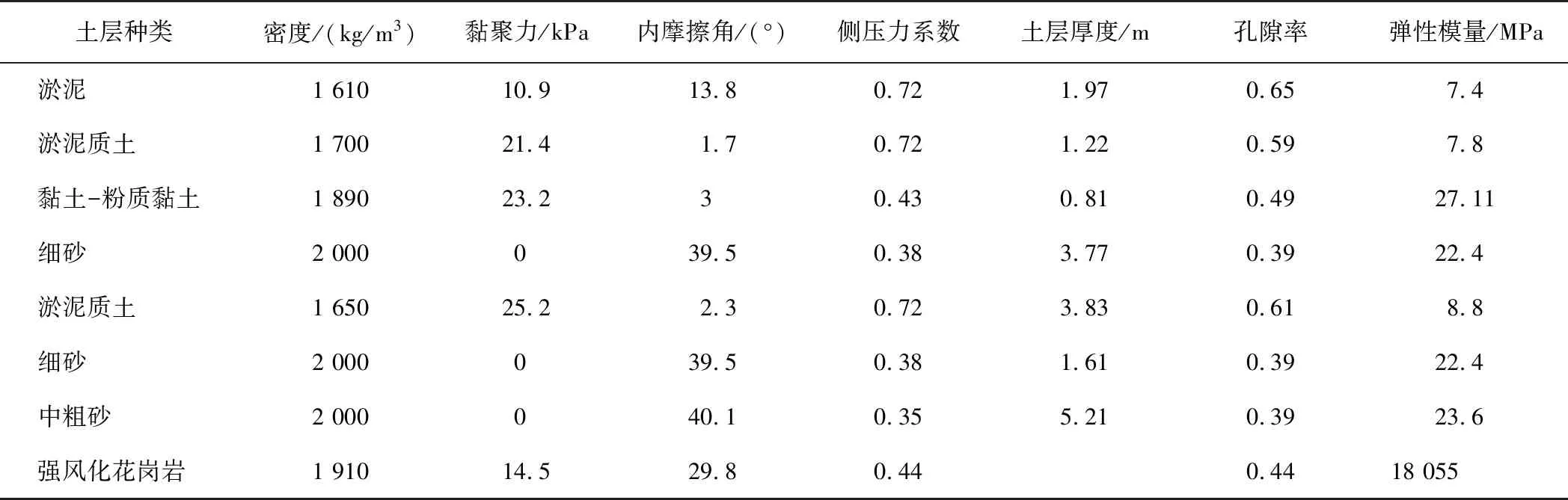
表2 土层参数

4.2 理论计算与数值模拟对比分析

基于某工程排水隧洞地质资料，利用第2节中的Terzaghi松动土压力理论和三维松动土压力理论分别计算隧洞开挖面顶部上覆土压力。然后，采用部分楔形体模型和本文提出的部分梯形楔形体模型，分别计算隧洞开挖面最小支护应力比。为了验证部分梯形楔形体模型计算的准确性，将数值仿真结果与理论计算结果进行了对比分析，计算结果见表3。

表3理论方法与数值仿真结果比较

Table 3 Comparison of theoretical methods and numerical simulation results

上覆土重理论计算模型部分楔形体模型部分梯形楔形体模型(本文)数值模拟方法Terzaghi松动土压力三维松动土压力0.7850.7340.7190.6930.690

由表3可知： 当采用Terzaghi松动土压力理论计算隧洞上覆土压力时，部分楔形体模型和部分梯形楔形体模型计算出的极限支护力应力比分别为0.785和0.734，计算结果比数值模拟结果(0.690)稍大，误差分别为13.8%和6.38%，误差相对较大，偏于保守；当采用三维松动土压力理论计算隧洞上覆土压力时，部分楔形体模型和部分梯形楔形体模型计算出的极限支护应力比分别为0.719和0.693，计算结果与数值模拟结果(0.690)基本一致，误差分别为4.20%和0.43%，误差较小。

对比2种楔形体模型计算结果发现： Terzaghi松动土压力理论计算的开挖面极限支护力应力比比三维松动土压力理论计算结果偏大；当采用同一上覆土压力理论时，部分梯形楔形体模型比部分楔形体模型更接近数值模拟结果，部分楔形体模型计算结果更加保守。综合分析可知，当采用三维松动土压力理论和部分梯形楔形体模型计算支护力应力比时，计算结果与数值模拟结果吻合较好，说明本文提出的部分梯形楔形体模型是适用的。

5 结论与建议

上软下硬地层在盾构隧洞施工中比较常见，合理确定开挖面极限支护力最小值是安全施工的重要保障。基于实际工程，对前人研究成果进行了总结和改进。通过模型计算和数值模拟技术，考虑隧洞开挖面孔隙水压力，合理计算了上软下硬地质条件下盾构隧洞极限支护力，得出如下结论与建议：

1)开挖面前方上下土(岩)体弹性模量之比对开挖面破坏有一定影响。当弹性模量之比小于0.3时，开挖面最大水平位移位于土(岩)层分界面上部。

2)基于刚体极限平衡原理，对三维梯形楔形体模型进行改进，提出考虑孔隙水压力条件下的部分梯形楔形体模型，并将该计算模型应用于实际工程中(上软下硬地层)，模型计算与数值模拟结果基本吻合。

3)分析了Terzaghi松动土压力理论和三维松动土压力理论对部分梯形楔形体模型计算结果差异性的影响，验证了采用三维松动土压力理论计算隧洞上覆土压力和部分梯形楔形体模型的组合方式相对可靠。

研究结果可为上软下硬地层隧洞开挖面极限支护力最小值理论计算及上覆土压力理论的选取提供参考。需要说明的是： 上述研究并未考虑渗流力对开挖面稳定性的影响，考虑渗流及盾构掘进因素的开挖稳定性需要进一步研究。