融合标签信息的卷积矩阵分解推荐算法
2020-03-13顾军华李新晨张亚娟董彦琦
顾军华 李新晨 张亚娟* 董彦琦
1(河北工业大学人工智能与数据科学学院 天津 300401)2(河北省大数据计算重点实验室 天津 300401)
0 引 言
自20世纪末进入信息化时代以来网络盛行[1],人们每天的活动与互联网密切相关,用户通过互联网获取所需信息的同时,网络上的有效信息也在增加,这样,人们从大量数据中获取所需的信息将会变得更加困难,这是“信息过载”的问题。推荐系统[2]就在信息过载问题的环境中应运而生,矩阵分解作为当前推荐系统中使用最广泛的算法之一,同时也在Netfix大赛中屡创新高,成为众多推荐算法中研究热门。
在推荐算法中通常使用两种类型的数据,一类是用户与资源的显式交互数据,如评分、收藏行为等,第二类诸如文本信息和关键字的属性。使用第一类型数据的推荐算法称为协同过滤[3]算法,而使用额外附加文本信息和属性描述数据的方法被称为基于内容的推荐[4]方法。在当下流行的推荐系统中,基于内容的推荐算法也会利用评分矩阵监督最终预测推荐,但该类算法更倾向于专注于单一用户评分而不是全部用户集,单一用户需求和约束是基于知识库的推荐系统的推荐标准,不使用历史评分记录。一些混合的推荐系统[5-6]联合上述算法与协同过滤算法,在推荐的性能表现上明显优于其他推荐算法并且鲁棒性更高。
在个性化推荐系统中,矩阵分解算法只是考虑单一的评分信息,造成严重的数据稀疏问题,使用附加的数据源是解决用户冷启动和稀疏性的一种简单有效的方法。2007年Salakhutdinov等[7]首次将深度学习模型玻尔兹曼机应用在推荐系统中;2011年Wang等[8]将主题模型结合概率矩阵分解模型,将资源的辅助信息融入隐向量;2014年Wang等[9]在之前的基础上,用降噪自编码器替换了协同主题模型,提取更深层次特征,达到了更高的预测准确率;2018年Huang等[10]提出了一种协同矩阵分解方法,即并行的对2个用户项目矩阵进行分解,共享用户潜在特征矩阵,在2个信息维度上求用户的潜在特征。张维玉等[11]为了提高推荐效果,提出了一种结合可靠性和信任关系的矩阵分解模型,缓解冷启动问题。2018年Wu等[12]提出基于上下文感知的半监督协同训练模型,通过上下文信息建立弱预测模型,并利用上轮基模型结果使用协同训练策略进行预测。上述的深度学习模型都是利用用户与资源额外信息输入,获得更深层次、更稠密的隐性表示,寻找用户与资源的非线性特征关系。但上述推荐算法均是基于矩阵分解的角度上提出改进,只考虑用户对资源的评分信息,这样的推荐解释会偏向于两个用户同时喜欢某个资源是因为资源中的相同理由,存在弊端。比如用户A和B同时喜欢“复仇者联盟”,但用户A是因为剧中的“钢铁侠”因素,而用户B是因为更喜欢其中“科幻”元素,如果是因为B喜欢而向用户A推荐,这样的推荐解释是不够准确的。而在基于标签的推荐系统上,可能“复仇者联盟”和“哈利波特”同样拥有“剧情”“科幻”两个标签,但熟悉这两部电影的用户知道,“复仇者联盟”在科幻的表达上要比注重剧情的“哈利波特”更受科幻迷的追捧,所以考虑到仅仅有标签是不够的。基于这个问题,我们使用深度模型来学习资源的语义信息表达,另外我们发现,学习额外信息的深度学习模型由于词袋模型方法的局限性,通常忽略文本表达的上下文语义环境,无法捕捉语境间词语的细微差别,在深度学习网络训练中损失一部分重要特征。
针对以上问题,我们提出了一种融合标签信息的卷积矩阵分解推荐算法TaSoConvMF,能够有效地在评分数据信息基础上,增加额外的多源数据信息、标签信息等辅助信息,有效利用了资源的描述信息,经过已经训练好的WordEmbedding向量作为输入层数据,并行地将输出的资源隐向量作为隐藏层的输入进行深度学习训练隐特征,将最后的输出作为表达资源的隐表示,再结合标签信息,进行内积交互,最后根据预测结果反向更新TaSoConvMF算法各层参数。在豆瓣评分数据集和MovieLens10M数据集上,TaSoConvMF算法在RMSE指标上达到0.83左右,比PMF算法在预测性能上提升了7.4%,比ConvMF在预测准确率上提升2.7%。
1 问题相关定义及概率矩阵分解
假设系统中有效用户集合被定义为U,有效资源被定义为I,用户的所有评分记录被表示为R,并且定义S为记录评分的可能值S∈{1,2,3,4,5},以rui表示这个记录,通常评分记录通过矩阵表示。定义对物品i进行评分的用户子集为Ui,那么Iu就是用户u操作过的物品子集。
推荐系统主要解决两个问题,即找到用户最喜欢的项目和最喜欢的K个项目。两个问题非常相似,以第一个问题为例,对于特定用户u,需要了解项目Iu是否最符合他的偏好。可以根据用户对项目的评分信息,将问题转换为回归或多类问题。目标是找到用户u对新项目i的预测分数f:U×I→S的映射函数。具体如下式所示:
(1)
式中:i*是推荐结果,ua是某个活跃用户。实际上,R一般分为两部分,一部分为训练集R_train,用于学习上面的函数f,另一部分是测试集R_test,用于测试函数f的性能推荐。用于测试函数f的度量指标可能因不同的推荐目标而不同,本文使用RMSE作为评价指标。
假设基于社会化标签的推荐系统中用户数、项数和标签数为N、M、K。评分数据满足R∈RN×M,用户矩阵、物品矩阵和标签矩阵分别用U、V和T表示,并根据文献[13]得到评分矩阵R的条件概率表达式为:
(2)
(3)
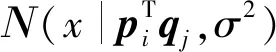
根据贝叶斯定理,用户和项目特征向量的后验概率分布如下式:
(4)
然而根据此式所得特征向量只考虑用户和项目维度的关联分布,第2节将会引入联合概率矩阵分解对用户、项目、标签三个维度关系进行建模。
2 算法设计
2.1 概率矩阵分解模型
根据第1节介绍的概率矩阵分解模型,假设用户的隐特征因子向量服从期望为零0的独立的高斯先验分布。在TaSoConvMF算法中,使用与式(3)同分布的高斯函数来表示用户的隐特征因子向量。然而,TaSoConvMF算法中项目隐特征因子向量不服从假设的高斯先验。项目隐特征因子向量由三个变量共同构成,它们分别是:项目描述文本矩阵Rawtextj、卷积神经网络中的共享权重矩阵W和加入的高斯噪声ε。如下式所示:
(5)
在卷积神经网络中,W作为总体共享权重矩阵是通过网络迭代更新后训练得到的,Rawtextj是项目j的文本输入矩阵,TaSoConvMF算法使用Word2Vec获得项目描述文本的输入数据矩阵,Word2Vec为深度学习模型的嵌入层。我们将在TaSoConvMF算法的神经网络部分讲解Word2Vec模型的处理过程。
在一个标签系统中,标签信息用来描述资源特征,在TaSoConvMF算法中,我们将所有的标签建立文档库,假设其含有K个标签,为T={t1,t2,…,tk},其中tk为第k个标签属性特征。我们采用TF-IDF来计算标签权重,则用户ui标注的标签tk的权重为:
(6)
资源vj被标注的标签tk的权重为:
(7)
式中:f(i,k)、f(j,k)表示标签tk在文档中出现频次,dik、djk表示带有标签信息的用户数量以及带有标签信息的项目数量。根据标签权重,计算出用户之间基于标签权重向量的相似性,将最近邻矩阵表示为P,同理,项目最近邻矩阵为Q,将最近邻融合到TaSoConvMF算法中概率矩阵分解模型部分。
根据用户标签权重矩阵和资源标签权重矩阵,使用余弦相似度计算方法计算最近邻之后,根据相似度结果排序,作为类似度高的邻接,将最近邻集合中排序前20用户集和资源集整合到模型中。如图1所示。
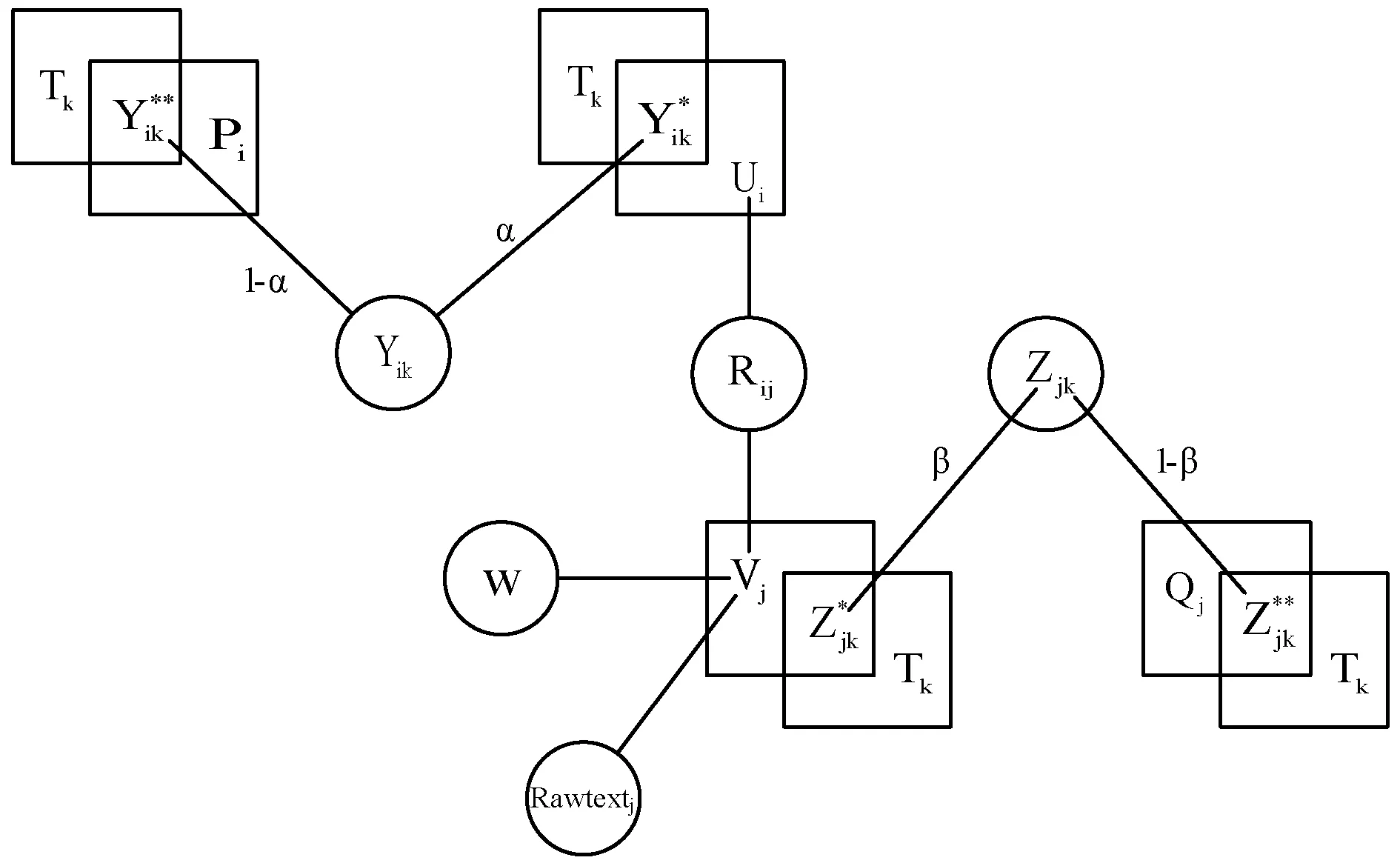
图1 TaSoConvMF模型
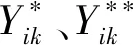
假设用户的隐特征向量、资源隐特征向量以及标签隐特征向量均服从期望为0的球面Gauss分布,则有:
(8)
(9)
(10)
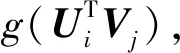
用户资源评分矩阵R的条件概率为:
(11)
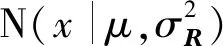
(12)
当用户在标签上加上标签时,它将参照α∈[0,1]标记其邻居的标签,α=0表示用户标签只受邻居用户的影响。
资源标签权重信息矩阵Z的条件概率:
(13)
当资源被标签时,用户将参照邻居标记的标签。β=[0,1]这将用于表示资源邻人的影响程度:在β=0的情况下,意味着资源标签都是由邻居资源影响的。
根据贝叶斯定理,三个矩阵的后验概率分布为:
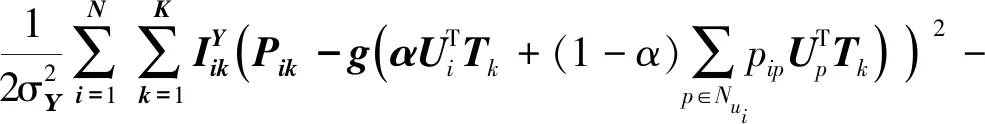
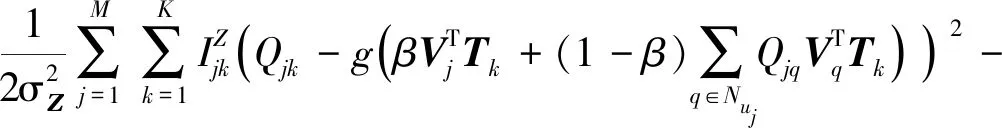
(14)
式中:l为隐特征向量维度。
最大化后验概率相当于最小化下式:
E(U,V,T,R,P,Q)=
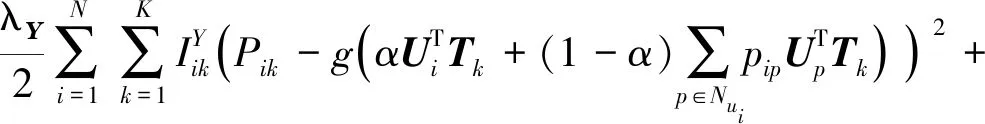
(15)
算法的时间复杂度是从后验概率分布式(14)和目标函数E的梯度下降法的过程中产生的。式(14)的队列R、Y、Z是数据疏散队列,目标函数E的时间复杂度为O(pRl+pYl+pZl),其中pR、pY、pZ分别表示矩阵R、Y、Z中的非零元素个数。可以看出,在大规模数据中,本算法仍然适用。
2.2 神经网络模型
TaSoConvMF算法使用卷积神经网络为资源的额外信息建立模型,其网络结构如图2所示。输入层将项目的原始描述文本转换为可以输入到网络中的数值向量。随后由特征处理层进行文本内容特征的处理,由输出层输出最后结果。接下来将描述TaSoConvMF算法中网络模型的每个层的详细结构和数据流过程。
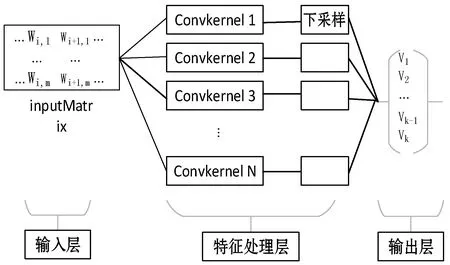
图2 TaSoConvMF算法中神经网络结构图
将原来的文件转换为在网络上输入的稠密矩阵。假设每个项目的文本信息由一系列单词组成。Rawtext=[word1,word2,…,wordn],Rawtext是n维向量,n是某个项目文本中的单词总数。要转换Rawtext数值矩阵,需要使用列向量替换向量中的每个单词。用等维度的向量随机初始化每个单词,也可以使用被训练好的Word Embedding作为Rawtext的单词填入的初始化向量。TaSoConvMF算法使用Word2Vec在训练词向量时。使用Word2Vec算法产生的词向量,具有比潜在意义解析等早期算法更多的优点。单词向量定位在语料空间中,使得在语料库中共享相同上下文的词语在空间中邻近。
假设一个项目中的单词向量维度是m,使n维的文本向量Rawtext变换为神经网络输入层的输入矩阵InputMatrix:
Rawtext=[word1,word2,…,wordn]
(16)
InputMatrix是m×n的矩阵。
在特征处理层中进行密集矩阵的特征提取。与手写数字识别方法不同,通常在图像像素矩阵中使用小滤波器(3×3)用于局部检测。文档矩阵中提取特征的过程则有些不同,是因为图像和文本具有不同的上下文关系,文本卷积应确保以单词为单位执行局部感知。
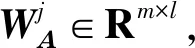
(17)
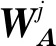
(18)
假设一种滤波器可以得到一种特征图,在卷积层中存在N个滤波器也就是存在N个数量的共享权重矩阵WA,则在最终获得N个卷积结果后,完成特征提取。
接下来,进行下采样处理。根据权值共享和局部感知所提取的特征的数量还很大,导致网络资源的极大浪费,下采样将有助于减少数据量,去除冗余数据并保存重要特征,同时网络会更鲁棒。在TaSoConvMF算法的下采样中,由于各条目的单词数不同,所以也解决了针对不同文本长度卷积维度的问题。下采样有几种方法,选择矩阵最大值作为样本值,另一方面计算矩阵所有值的样本平均值作为样本值。TaSoConvMF算法选择平均抽样取样,由式(18)中Aj的平均值作为当前卷积核的采样值,使得特征处理层的结果可以作为输出层的输入。
输出层接受采样层的输出向量,经过输出层映射得到最终结果。TaSoConvMF算法利用卷积神经网络将原始项目描述文本转换为项目隐特征向量,要保证输出层的维度要与项目隐特征因子数k相等,通过下式向k维空间进行映射:
Output=tanh(Mat_P2[tanh(Mat_P1·Mean(A)+
bias_P1)]+bisas_P2)
(19)
式中:Mat_P1和Mat_P2为映射矩阵,且Mat_P1∈Rf×N,Mat_P2∈Rk×f,bias_P1和bisa_P2都是偏置项,Mean(A)是特征处理层下采样的结果,Qutput是输出的结果,且Output∈Rk。
输入和输出数据如表1所示。
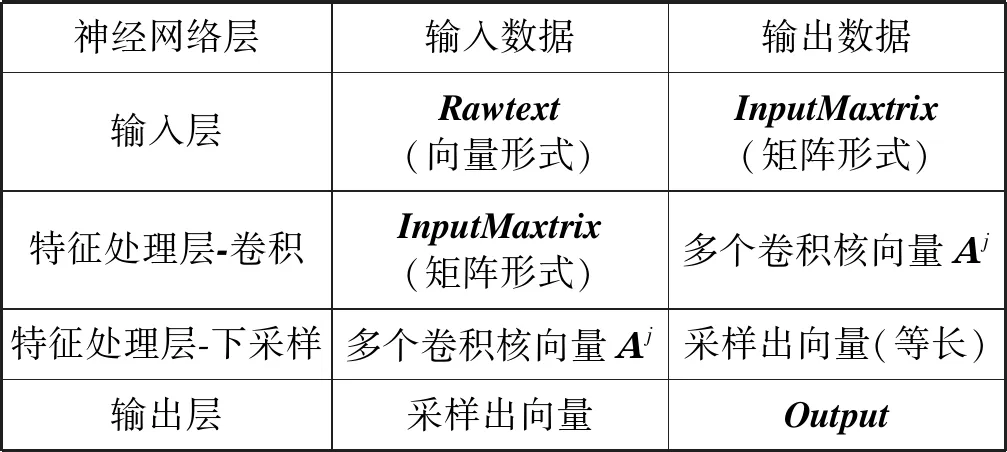
表1 TaSoConvMF算法中各层输入与输出
2.3 TaSoConvMF模型求解
TaSoConvMF算法有许多参数。本节重点介绍如何在TaSoConvMF算法中求解参数。从上一节可以看出,TaSoConvMF算法的概率矩阵分解部分和神经网络部分都需要用户隐式矩阵U、项目隐式矩阵V、标签隐式矩阵T、卷积神经网络的神经元权重W和偏置项bias。贝叶斯解决方案目标为:
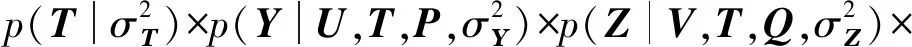
(20)
最大化后验概率式(20)相当于最大化式(21),对其取负对数得到式(22):
(21)
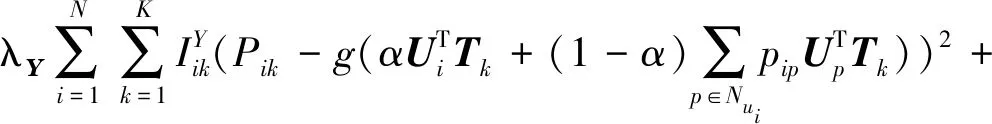
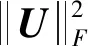
(22)
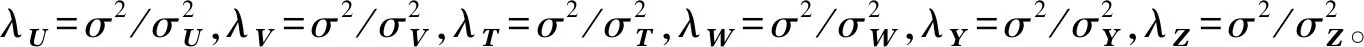
从式(22)可以看出,等式右部分中:
(23)
与概率矩阵分解没有区别,添加卷积神经网络来处理项目的文本等同于原始正则化项。
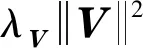
TaSoConvMF模型的求解方法,采用传统的梯度下降算法进行更新,对深度学习框架中的权重矩阵,采用逆向传播进行更新。
TaSoConvMF算法可以获得用户隐式矩阵U、项隐式矩阵V、标签隐式矩阵T、神经元权重W和偏移bias,有了这些参数,TaSoConvMF算法就可以对用户观看的项目进行评分预测,并通过定量分析算法的预测性能。
3 实 验
3.1 数据集介绍与处理
TaSoConvMF算法使用豆瓣电影数据集进行性能验证和比较实验,本节介绍了对豆瓣进行爬网的爬网逻辑和结构。
爬虫是使用基于开源框架Scrapy开发的。爬行URL列表的数据流和内容如图3所示。
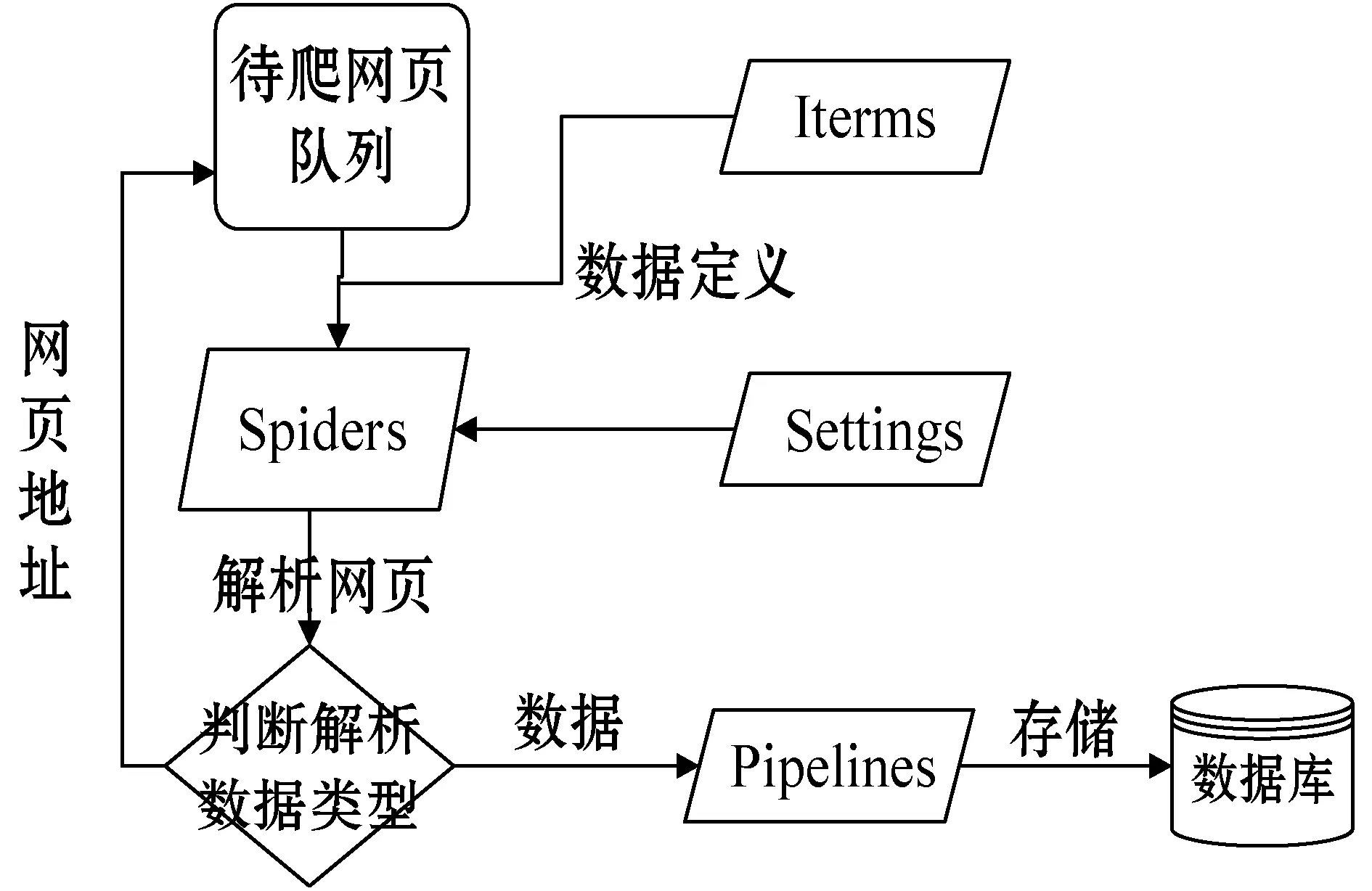
图3 豆瓣数据集爬虫结构图
1) Spiders是爬取DoubanSet数据集的中心部分。由于豆瓣电影需要登录大量信息,因此首先必须实现Spiders的用户仿真登录功能。在此模块中,主要使用XPath搜索项目数据的数据块,使用正则表达式过滤目标数据。
2) Items是DoubanSet数据集的数据定义部分。
3) Pipelines用来存储DoubanSet数据集,网页文本信息经过解析后的Items样式的目标数据流到管道存储在数据库中。
4) Settings用来设置参数。设定根据模块的曲柄所需的参数。例如:设置响应优先级、设定URL的自由间隔、设定IP地址不会禁止的设定、设置爬虫深度等。
最终得到DoubanSet数据集及实验中其他数据描述如表2所示。
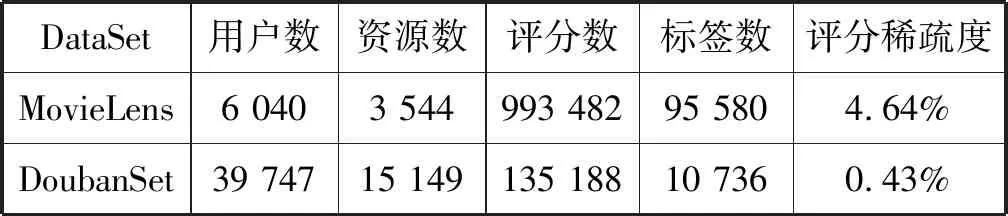
表2 豆瓣数据集和MovieLens数据集
其中:DoubanSet数据集有12 842条的资源描述文档信息;用户对资源的评分是1~5的整数,分数高低表示用户对电影的喜爱程度;稀疏度为评分数占用户数与资源数乘积的比例。
3.2 实验设计
DoubanSet数据集以8∶1∶1分配,相当于训练集、测试集和该实验所需的验证集。实验平台为一个20 GB的Intel 3.4 GHz系列处理器和16 GB内存工作站。
本次实验使用Gensim工具包对项目描述文本构建词向量训练。Gensim工具包封装了诸如文本主题与分析算法等模型。在Gensim中只需提供足够的语料(分词等预处理后)和维度,调用Word2Vec。Word2Vec(sentences,size)函数可以快捷地训练词向量。
Keras框架用于学习TaSoConvMF算法的项目描述文档。目前已有的学习工具包括:TensorFlow、Kerasa、Terano、caffe和MxNet等。其中,Theano网络训练速度不够快;Caffe不支持递归神经网络。Keras不需要手动编写网络层,通过声明API就可以亲自实现想要的神经网络。
TaSoConvMF算法中有许多参数影响最终算法得分预测结果。对比实验主要从以下几个关键因素进行:
1) 由描述文档语料训练出来的词向量是否有效。由于用户的评论被用作词向量的训练语料库,在分词、去除停用词等过程后所剩的与项目内容相关联的词非常少,因此,在实验中需要检测我们所使用的词向量是否有效。
2) 从式(22)可以看到参数λU与λVλT本质上是一般的正则化项系数,尤其λV的大小直接关系到神经网络部分在整个损失函数中所影响的比重,三者的取值对TaSoConvMF算法有很大意义。
3) 隐含因子数。对于矩阵分解推荐算法,隐藏因子的数量k是一个重要的影响参数。TaSoConvMF算法的本质是概率矩阵分解模型,k值也影响到网络的输出维度。实验中通过设置不同k值分析RMSE的变化趋势。
4) 词向量的维度。词向量维度作为神经网络的输入维度,影响网络结构。维度在一定程度上会影响“词嵌入”的质量,维度越高,词向量表达越准确。
3.3 实验结果与分析
3.3.1算法性能验证
TaSoConvMF算法主要参数设置为:k=50,d=200,λU=λV=λT=10,η=0.01,λY=λZ=0.5,α=0.6,β=0.4。
DoubanSet数据集的实验结果如表3、表4、图4所示。可以看出,TaSoConvMF算法的RMSE为0.899 6,小于PMF的0.944 0,小于ConvMF的0.921 2,性能提升约4.7%和2.3%,这表明TaSoConvMF优于PMF和ConvMF。实验中,为了不失通用性,增加TaSoConvMF算法在MovieLens 10 M数据集下的(在下文中称为MLS)实验验证。PMF的RMSE约为0.89,TaSoConvMF算法的相应误差为0.79。此外,由图4可知,与豆瓣数据集相比评分预测标准数据集MovieLens更准确,性能提高率更高,改进的TaSoConvMF算法提升约7.5%。
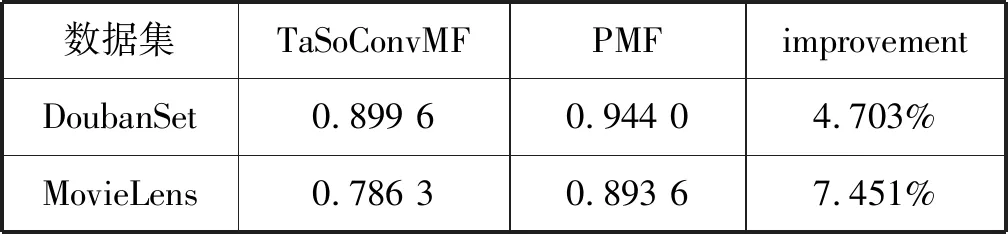
表3 TaSoConvMF与PMF在RMSE指标上的对比结果
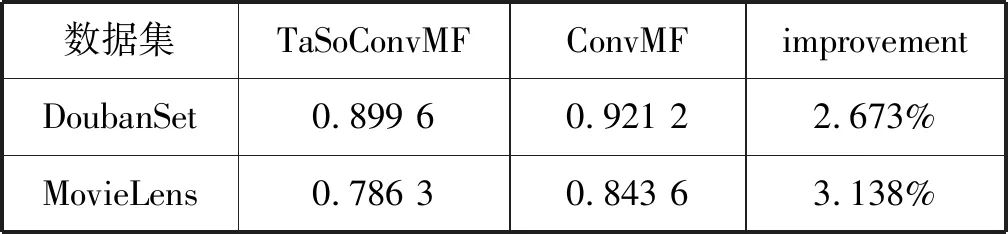
表4 TaSoConvMF与ConvMF在RMSE指标上的对比结果
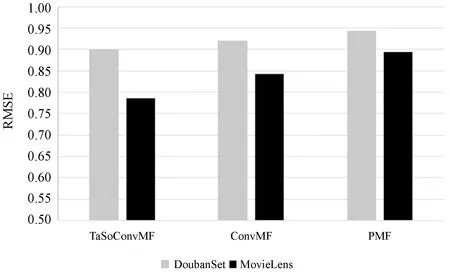
图4 TaSoConvMF与PMF在不同数据集上的实验结果
在实验中发现用户兴趣可以被准确预测,使用文本信息结合深度学习矩阵分解推荐算法TaSoConvMF进行有效学习。使用DoubanSet数据集和MLS10M数据集来比较ConvMF算法。
实验结果表明,针对同一算法结合文本信息的协同矩阵分解进行推荐的实验效果更准确。
3.3.2正则化项对算法的影响
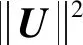
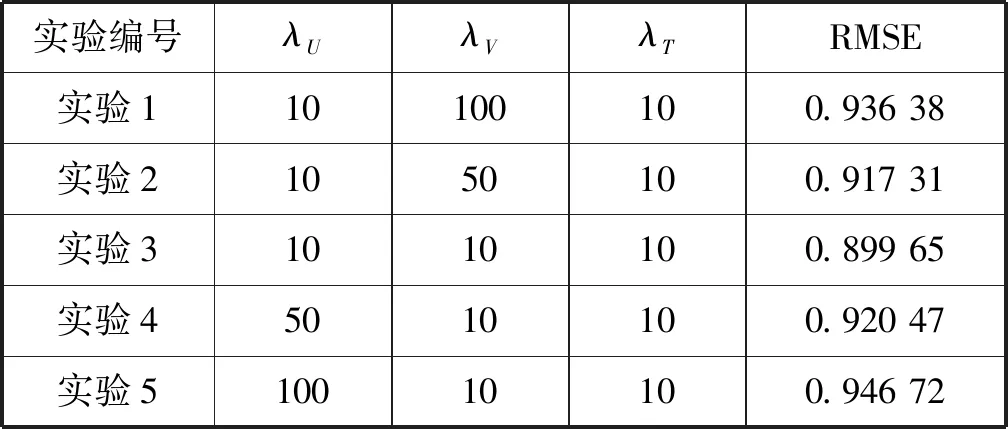
表5 五组不同λU和λV取值的实验结果
表5中,先固定λV、λT为10,得到RMSE随λU变化的折线变化如图5所示。接着固定λU、λT为10,RMSE随λV变化的折线变化如图5所示。可以看出,RMSE与三个平衡因子呈线性关系,并且随λU、λV、λT的变化而变化。另外,λU的变化对RMSE的影响是合理的,且影响大于λV。
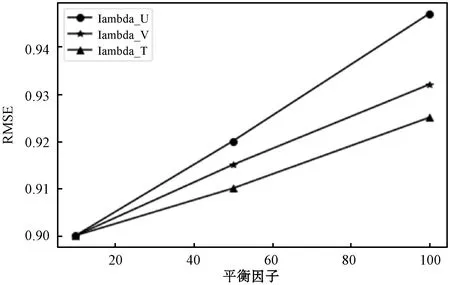
图5 λU、λV、λT对RMSE的影响
取λU作为x轴,λV作为y轴,RMSE作为z轴建立坐标系并绘制3D表面如图6所示。可以看出,由这三个坐标形成的空间表面近似于空间三角形,其中在λU=10、λV=10时预测性能最好,λU=100、λV=10时预测性能最差(即接近坐标原点的RMSE更低)。该空间三角形证实了从图5得到的结论:RMSE与三个平衡因子呈线性关系,并且在两两平衡因子的实验中显示出相同的性质。
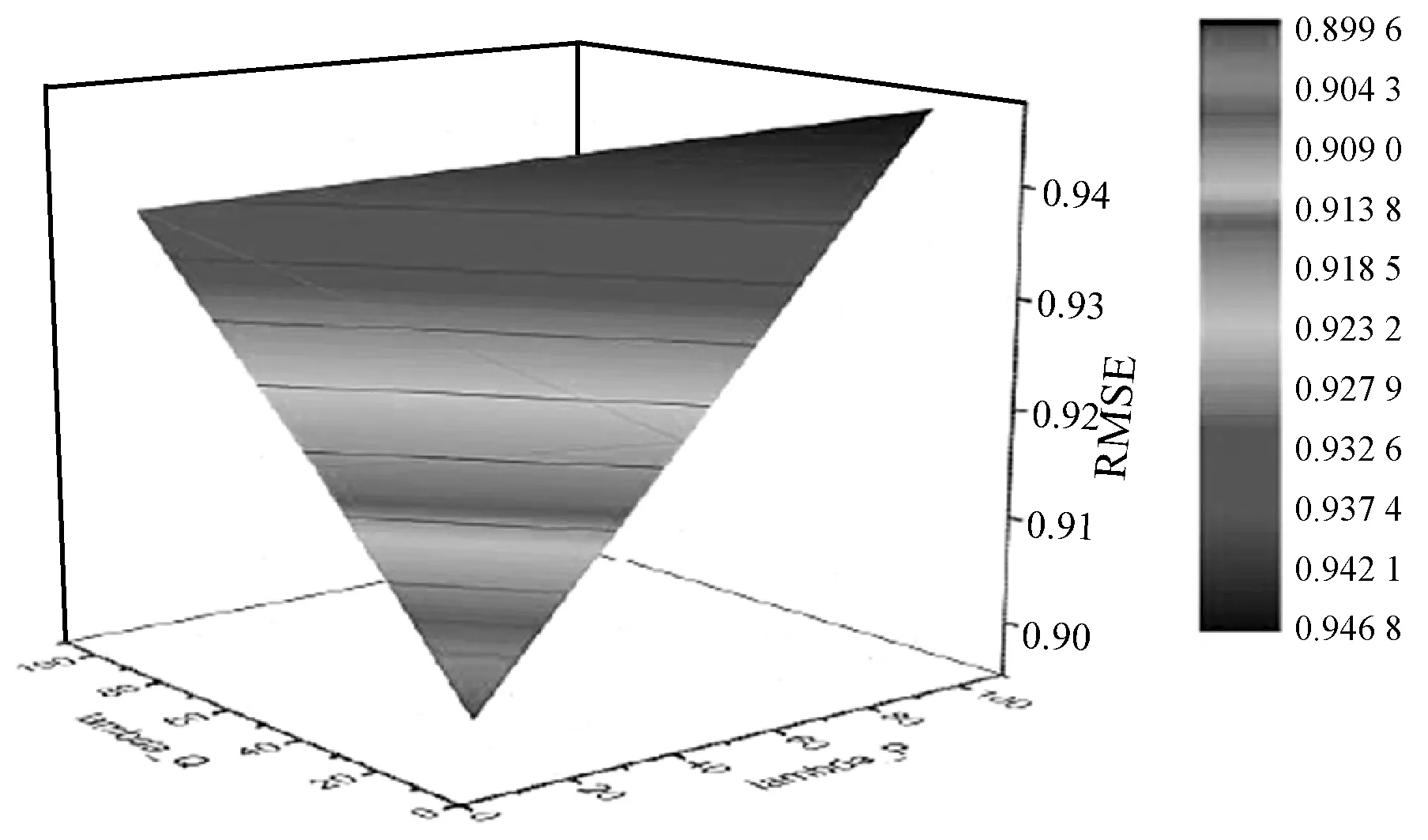
图6 λU、λV平衡因子与RMSE三维曲面图
3.3.3邻近因子对算法的影响
参数α和β用来控制调节邻近用户或项目对算法的影响程度,图7及图8分别显示参数对RMSE的影响。首先设置初始值β=0.5,根据RMSE调整α的取值范围,当取到α的最优值后测试β的最佳效果,直至α和β达到最优组合。从实验结果看出,α=0.6,β=0.4时推荐效果最佳,即用户在标注标签时,60%会根据自身认知进行标注,40%会根据邻近用户情况进行标注。
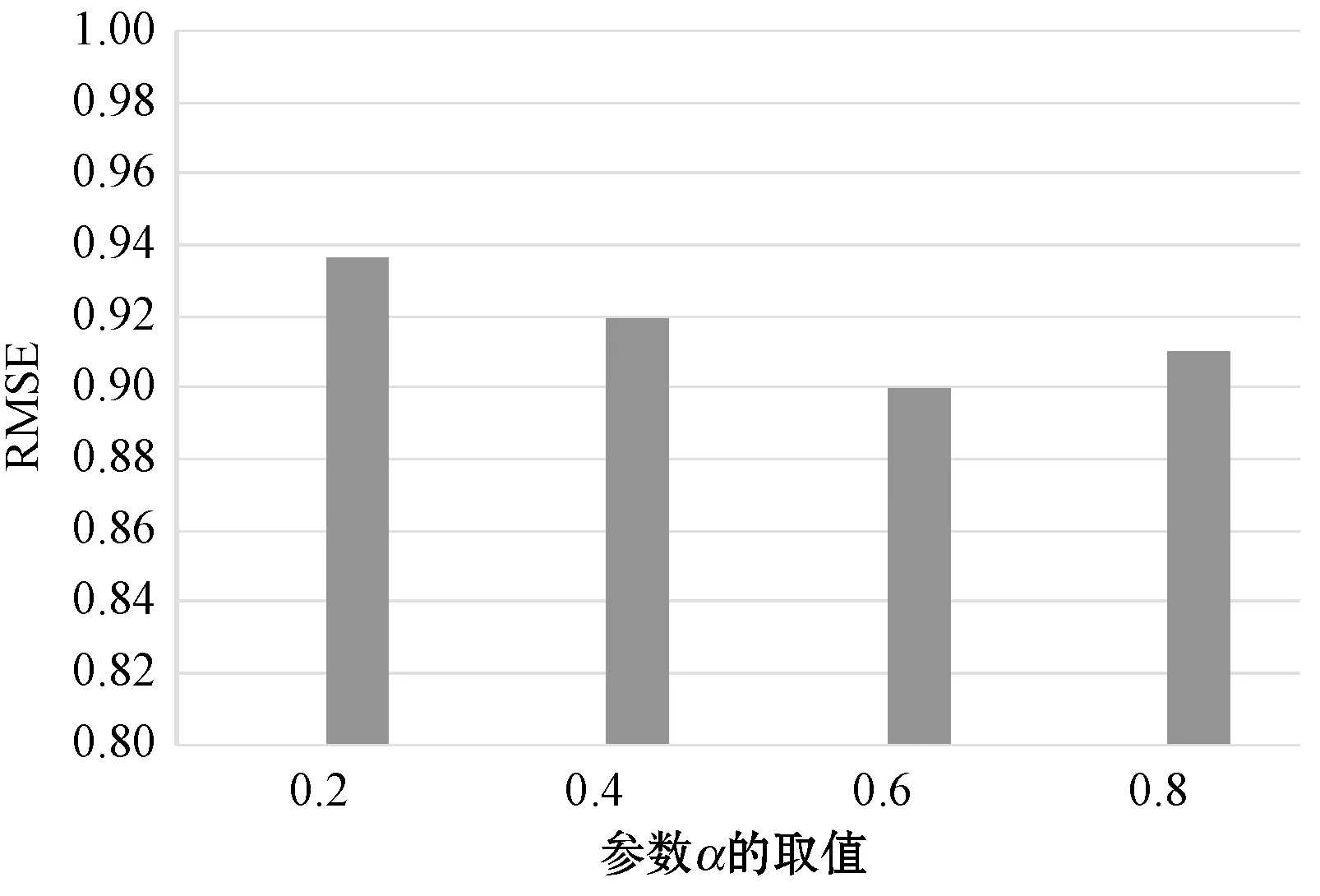
图7 参数α的影响
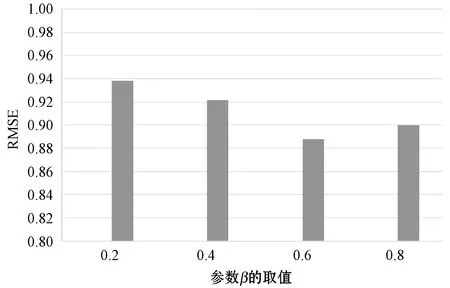
图8 参数β的影响
3.3.4对算法影响因素的分析
首先,本文研究了矩阵隐含因子的影响。在K为30,50,70(λU=10,λV=10,λT=10,d=200)的情况下,实验结果如表6所示。通常基于矩阵分解模型的最终结果会受到K值选择的影响。从实验结果来看,K值变化对RMSE的影响在结果的小数点后第4位才得到反映,这表明TaSoConvMF算法对小范围内K值的变化不敏感。从每轮训练所花费的耗时来看,各个实验间没有明显区别,约1 570 s。从训练轮次数来看,当K值为50时,训练轮次总数最大,为20;当K值为30时,训练轮次总数最小,为16。
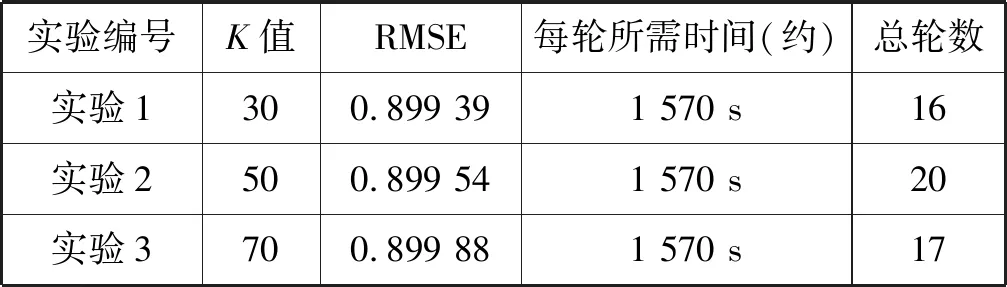
表6 K分别取30、50、70时的实验结果
为了测试不同的K值下每轮算法的RMSE,使用验证集数据绘制出如图9所示折线图。从迭代开始,实验1在第一次迭代中取得了显著的性能提升,RMSE从1.46很快降至0.89,收敛速度非常快;然而,实验3在第一轮迭代中,虽然RMSE最小,但收敛最慢。实验在第八次训练后均达到稳定状态。因此,为了使TaSoConvMF算法快速达到稳定状态,我们选择较小的K值。
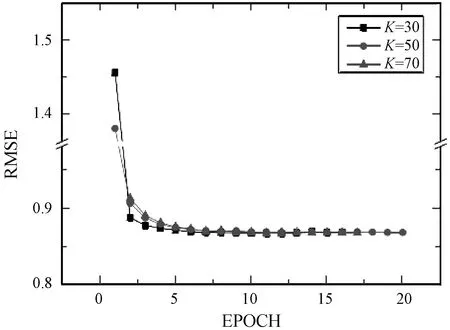
图9 TaSoConvMF在不同K值下迭代过程
最后,本文研究了单词向量对TaSoConvMF算法的影响。当d为100,200,300(λU=10、λV=10、λT=10、k=50)时,实验结果如表7所示。从实验的角度来看,无论d值如何,都可以忽略最终RMSE指数的差异。并且所有RMSE的值都约等于0.899,这与K取不同值的结果相同。然而,实验5每轮训练所需的时间是实验4是2倍,实验6是实验5的1.55倍,非常耗时。
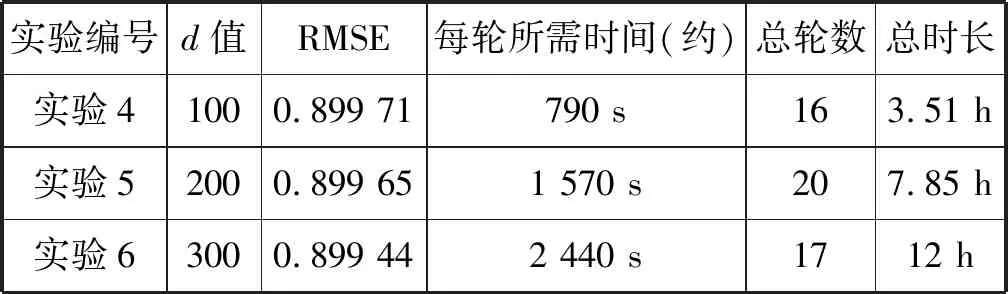
表7 d分别取100,200,300时的实验结果
图10显示了实验4、实验5、实验6的验证集中RMSE的变化。可以看出,d的值越大,初始循环时RMSE的值越小,说明初始值是否准确直接影响了TaSoConvMF算法的效果。从第二轮开始,初始价值所带来的好处逐渐减弱。实验4具有最快的下降速率,并且RMSE倾向于早期稳定。实验6的初始RMSE最小,但收敛状态最慢。
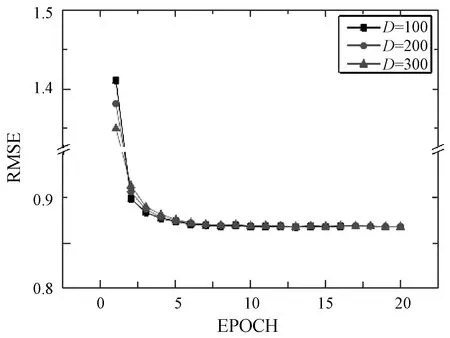
图10 TaSoConvMF在不同d值下迭代过程
基于上述分析,K值和d值在一定范围内变化,最终预测效果不是很大。对于有限的实验条件,可以选择小K值和d值(尤其是K值)来加快模型训练。
4 结 语
针对当前推荐系统冷启动问题导致的推荐效果不准确问题,本文提出了一种融合标签信息的卷积矩阵分解推荐算法TaSoConvMF。该算法使用卷积神经网络处理资源文档特征,利用标签矩阵和评分矩阵挖掘用户和资源的隐含关联,利用误差逆向传播与坐标下降法对算法进行模型求解。通过在DoubanSet等数据集上的多组实验,验证了TaSoConvMF算法预测的准确性,并且给出了参数选择上的优选方案。
