一种分割脑部磁共振图像的FCM改进算法

杨 阳 沈艳冰 李 竹

(山西师范大学物理与信息工程学院 山西 临汾 041004)

0 引 言

脑部图像分割是基于MRI和一定标准下的相似性，将脑部MRI中相似度大的像素划分为相同的组织类，反之划分成不同的组织类。由于MRI成像过程的特殊性，MRI常存在不同程度的噪声、灰度不均匀和边缘模糊的现象[1]。因此，基于模糊理论的FCM算法在MRI分割上得到了广泛应用，已获得众多研究人员对FCM算法进行研究与改进[2,15]。然而，传统模糊聚类的图像分割算法因未考虑空间特性从而导致分割效果受噪声、异常值、成像伪影等影响较大，鲁棒性差。

为解决上述缺陷，部分学者引入空间特性到模糊聚类分割算法的目标函数中并应用于脑部MRI分割，取得了较好的分割效果。其中，Ahmed等[8]将局部空间限制项引入到FCM的目标函数中，提出FCM-S算法。该算法利用像素与其邻域像素在特征值上的连续性，克服噪声对图像分割的影响，但每次迭代都要计算一次邻域导致计算量大。此后， Chen等[9]利用邻域内的像素均值或中值取代FCM-S算法中的邻域信息，提出快速FCM-S(FCM-S1，FCM-S2)算法。该算法应用于噪声轻度污染的脑部MRI时效果较好，当噪声过度时，此算法效果不佳。为了克服这个缺陷，Zhao等[10]基于非局部空间信息提出了一种FCM-NLS算法。该算法使脑部MRI无论处于何种程度噪声污染下都能获得较优的结果。但该算法仍有三个缺陷：一是采用随机处理方式初始化分割类中心、分割类别数，导致可能收敛到局部极值，尤其对于分割相似度较小的类别时，同一幅脑部MRI的数次运行结果可能差异较大，稳定性差；二是引入空间信息在一定程度上令算法复杂性提高，运算效率下降；三是算法适用于凸数据集图像的聚类分割，而MRI中部分细节不属于凸数据集，使得算法不能较好地处理MRI部分细节。对于非凸数据集图像的聚类分割，一些学者引入核函数来进一步计算像素间相似度及空间信息相似性[11,13]，改进的算法适用于不同数据类型的聚类分割，提高了算法性能。

针对应用于MRI分割的FCM改进算法出现的缺陷，本文提出一种FKFCM-NLS分割算法。算法引入直方图、K-means法，对分割类别数、初始分割类中心进行最优选取，避免收敛不到全局最优值；在目标函数中引入核函数和基于积分图的非局部空间信息以降低计算的复杂性，提高算法抗噪性，算法性能更优。

1 基本原理

1.1 Mercer核

假设输入空间的样本xk∈Rl，k=1，2，…，N，Rl表示低维空间的样本实数集。当样本X经过某一非线性变换映射到某一特征空间H时获得Φ(x1),Φ(x2),…,Φ(xN)，映射前后的样本数据分布图如图1所示。

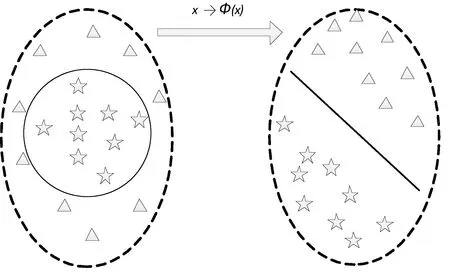
图1 输入空间到特征空间的映射

输入样本在H空间就可以用Mercer核[11,13]来表示：

K(xi,xj)=Φ(xi)·Φ(xj)

(1)

目前，常用的核函数有：

(1) 多项式核函数K(x,y)=(x·y+1)d，其中，d是自定义的整数。样本的边缘点对d的取值影响较大。在实际的使用中，阶数d常控制在一个较小的范围内，且不易确定。

(3) 两层神经网络sigmoidal核函数K(x,y)=tanh(-b(x·y)-c)，其中,b、c是自定义参数。该函数的参数值选择比较复杂和困难，只有b和c取特定值可用，且当b取值较小时性能与高斯核函数σ取较小值时相同，使用起来没有优势。

综合以上分析，本文采用高斯核函数作为映射函数。

1.2 非局部空间信息

在待测试的图像中X={x1，x2，…，xp，…，xn}，对应像素j的非局部空间信息ηj[11-12]为：

(2)

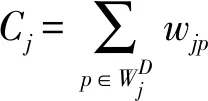
(3)

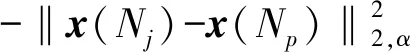
(4)

2 算法设计

针对脑部MRI分割结果受分割类别数、分割类中心初始值、噪声影响和运算量大的问题，本文提出一种基于积分图的非局部空间信息的快速模糊C-均值核聚类图像分割算法。

2.1 分割类别数选取

基于直方图可以直观地观察同一类型数据的遍布情况，本文采用直方图来确定分割类别数。

图2为无噪声的脑部MRI及其直方图。图中出现峰值表明该峰值相对应的灰度值出现的概率较大，相似度较高，分割时可划分为一类，该直方图约有4个峰值，故脑部MRI可粗略地划分为4类。结合生物学特性来看脑部MRI本身，其主要包含脑白质、脑灰质、脑脊液和背景区域4部分。因此，分割类别数选4比较合适。

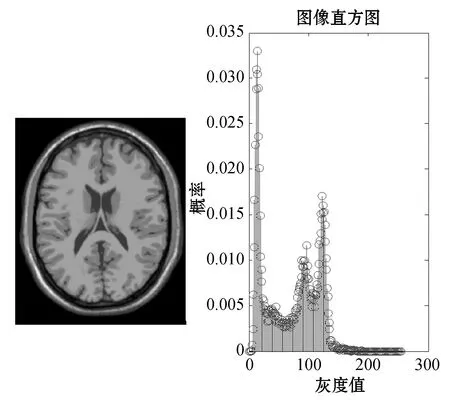
图2 脑部MRI及其直方图

2.2 初始分割中心选取

文献[14]对比了几种优化FCM聚类中心的方法，其中K-means法运行速度最快。本文选择基于K-means法来优化FKFCM-NLS的聚类中心，避免分割结果收敛到局部极值。

K-means法目标函数迭代式为:

(5)

式中：K是聚类个数；xj是聚类样本第j个像素灰度值；ci是第i类的聚类中心。

根据lagrange multiplier法，聚类中心分别为对应类中各数据点的均值。其迭代式为：

(6)

2.3 基于积分图的非局部空间信息

针对Zhao等提出的FCM-NLS算法复杂性高，运行速度慢的问题，本文在目标函数中引入基于积分图的非局部空间信息，利用积分图对其中两两矩形邻域间相似度运算进行加速，以提高算法的运行速度。

基于积分图的非局部空间信息函数式与式(2)一致，其中两两矩形邻域间相似度运算采用积分图进行加速。

矩形搜索块大小设为D×D(D=2Ds+1)，邻域块大小设为d×d(2ds+1)。矩形邻域块与当前块距离如下所示：

St(z)=‖x(Nj)-x(Nz+t)‖2

(7)

式中：t=p-z∈[|-Ds+Ds|]2是一个平移矢量。

构造一个关于像素差值的积分图像：

(8)

式中:j=(j1,j2)。

积分图递归计算式如下：

∀j=(j1,j2)j1≥1，j2≥1St(j)=St(j)+St(j1-1,j2)+St(j1,j2-1)-St(j1-1,j2-1)

(9)

欧式距离计算公式如下：

(10)

2.4 目标函数、隶属度及分割类中心

基于以上理论知识，通过引入核函数和基于积分图的非局部信息将本文目标函数修改为：

(11)

式中:uij为样本像素灰度值xj对第i个分割类中心的隶属度；m为模糊因子，其值大于1，通常在1．5～2．5之间取值；1-K(xj,vi)为样本像素灰度值xj到第i个聚类中心的距离；参数β控制了非局部空间限制项的惩罚作用；像素j的空间非局部信息由式(2)计算。

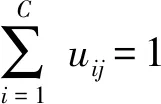
(12)

依据式(12)，分别求uij、νi和λj的偏导数，令其偏导均为0，求得隶属度及聚类中心函数：

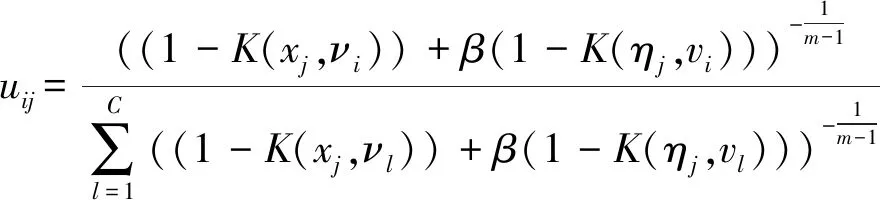
(13)

(14)

2.5 算法步骤

FKFCM-NLS算法步骤如下：

1) 依据直方图设置聚类类别数C。

2) 设置最大迭代次数lmax、迭代前提条件ε>0、加权指数m，基于积分图的非局部空间信息限制项的惩罚因子β，非局部滤波参数h，搜索块大小D×D，相似块大小d×d。

3) 依据K-means法确定分割类中心ν，随机初始化隶属度矩阵U=[ui j]n×c。

4) 利用式(2)计算图像像素的非局部空间信息ηj。

5) 选择高斯核函数并计算出核矩阵K。

6) 依据式(13)对U进行迭带更新，依据式(14)对ν进行迭带更新。

7) 每次迭代更新后，都计算此次更新后的迭代值J，并与迭带前的迭代值J′相比较。若|J′-J|≤ε，则退出循环，否则执行步骤6。

3 仿真实验

本实验通过对含噪不同的脑部MRI进行分割测试验证本算法的性能，利用FCM-S1、FCM-NLS以及本文所提KFCM-NLS算法分别对脑部MRI进行测试与比较[19-20]。所有实验均使用MATLAB 8.3，在联想 Intel(R) Core(TM) i3-2120 CPU，内存4.00 GB的PC机上运行。参数设置：m=2，lmax=300，ε=10-3，β=6，d=7，D=21，h=10。

实验所采用的脑部MRI测试图均为Simulated Brain Database数据库中T1模态、icmb协议下，切片厚度为1 mm，灰度不均匀水平为0的正常脑部MRI。图3为噪声水平为0的脑部MRI。

图3 MRI无噪声图

实验采用不同分割算法对噪声水平为3%与9%的脑部MRI进行测试。脑部MRI含噪图及测试结果图如图4所示。

(a) 含3%噪声 (b) 含9%噪声图4 脑部MRI含噪图及三种算法结果图

对于噪声水平为3%的正常脑部MRI，三种算法的去噪性能相似，测试结果图分割较完整，能将脑白质、脑灰质、脑脊液从背景中抽离出来。结合表1的客观评价数据对比得出，三种算法均能够获得良好的分割结果，其中，FCM-S1算法运行速度最快，其次是KFCM-NLS算法，最后是FCM-NLS算法。对于噪声水平为9%的正常脑部MRI，FCM-S1算法的测试结果图显示出明显的分割不足的现象，局部分割结果受噪声影响大，不能较好地区分含噪9%图中的部分区域，分割性能变差。但本文所提FKFCM-NLS算法和FCM-NLS1算法对含噪9%脑部MRI的分割结果均同3%含噪测试结果图差距微小，即对于不同水平的噪声，FCM-NLS算法和本文FKFCM-NLS算法都能将目标准确分割出来。结合表1的客观数据可以看出，FCM-NLS算法耗时最长，而在保证分割质量良好的情况下，FKFCM-NLS算法耗时较短，性能更优。综合以上分析，对于含噪不同的脑部MRI，FKFCM-NLS算法均具有良好抗噪性和较高的运算效率。

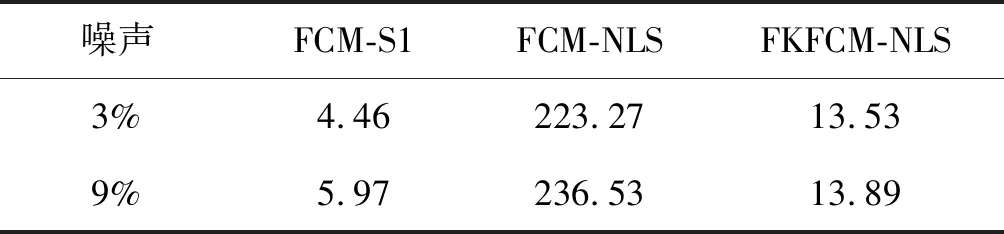
表1 算法运行时间 s

为了评价以上三种算法的优点及不足，本文引入错分率(MCR)来进行判断，MCR∈[0，1]，其定义为：

MCR越小表示分割效果越好。表2给出了测试中三种算法在脑部MRI含噪3%以及9%的情况下的错分率。从表2客观数据可以得出，对于含噪3%脑部MRI，三种算法的错分率差别微小，性能良好。对于含噪9%脑部MRI，由于含噪水平较大，像素的邻域像素也可能含有噪声。而FCM-S1算法在分割时只考虑了邻域间相似性，致使算法错分率较大，性能差。FCM-LNS算法引入像素的非局部信息进行分割运算，令算法错分率减小，性能良好，但算法复杂度高。FKFCM-NLS算法引入核函数和基于积分图的非局部空间信息，进一步减小了算法错分率，提高了算法运算效率。因此，在同等含噪情况下，本文算法性能最优。

表2 算法错分率 %

4 结 语

针对FCM-NLS算法分割脑部MRI时，可能收敛到局部极值及鲁棒性差的问题，本文提出一种FKFCM-NLS 算法。采用K-means算法确定分割类中心初始值，利用直方图获得分割类别数，解决了分割结果不稳定的问题；运用核函数计算样本间相似性，引入一个基于积分图的非局部空间信息限制项，降低运算复杂度，提高算法抗噪性能。客观评价数据及分割结果图表明，对于噪声污染过度的脑部MRI，本文所提FKFCM-NLS算法有较好的分割结果及较高的运算效率。