基于项目合作的社会关系网络中核心社团发现
2020-03-13王其冬周艳春何贤芒
王其冬 李 东 周艳春 何贤芒
1(宁波大学商学院 浙江 宁波 315200)2(国家自然科学基金委员会信息中心 北京 100085)3(辽宁大学商学院 辽宁 沈阳 110036)4(东莞理工学院网络空间安全学院 广东 东莞 523808)
0 引 言
近年来,社会关系网络的研究逐渐成为学术界研究的热点。由于社交网络的繁荣发展和广泛应用,越来越多的研究者将其科学研究和应用开发的注意力集中到社会关系网络这种虚拟世界中。社会关系网络分析已然成为社会学、地理学、经济学、信息科学等诸多学科的重要研究内容。基于社会关系网络结构进行数据挖掘和潜在模式分析比传统数据统计分析更加科学、效果更好、应用前景更突出。随着研究的深入,人们发现许多实际关系网络具有一定的社团结构,也就是说,整个社会关系网络是由很多个社团组成,社团之间的连接比较稀疏但社团内部相对稠密。社团发现是利用社会关系网络本身结构挖掘出模块化的社团结构。社团发现有利于人们更加深入去理解整个网络的结构、功能,而且基于社会网络的其他技术研究往往以社团发现的结果作为依据。
帕累托法则(Pareto’s Principle)[1],又称二八定律,不仅体现在经济学领域中的财富分布,也同样适用于社会关系网络中。这种现象在互联网社交平台得到了量化的数据支持。比如在Twitter[2]里,1%的人贡献了超过50%原创内容,而其他99%的人是转发其他人的内容为主。在微博上,流量明星拥有众多的粉丝和粉丝群,而普通的使用者则只有几十几百的粉丝,这二类不同的网络社交用户是如何互动的呢?有其潜在的内部结构吗?在社会关系网络中,社团发现已经被广泛研究。目前,学者们已经提出了很多算法,比如谱聚类算法[3]、(α,β)-聚类[4]、基于传导方法[5]、主题建模方法[6]、贪心算法[7]等,这些方法都有一个共同的特点,没有考虑社会关系网络中内部的结构。
从事自然科学基础研究的群体,即通常所说的科学共同体,存在一种天然的社团结构和关系,而且是显而易见的,这就是一个课题的负责人和参加者。我们利用国家自然科学基金申请者和参加者的数据,构建图结构做此方面的研究,得到非常有趣的结果,这个结果对基金管理者或许有一定的启示。
在国家自然科学基金委员会历年申请人与参与人构成的网络中,由于学科代码的不同,将申请人与参与人分成8个学部,45个科学处,科学处之间有交叉学科,也有不交叉学科。简单地看,似乎申请人就是有影响力的人,然而并不是所有申请人都是影响力显著的人。本文即是以项目合作关系网络为基础,根据这种关系网络的结构去设计特定的算法,在此基础上进行核心社团发现,就是寻找真正影响力的基础研究人员,而这些人才是基础研究的中坚力量,我们可称这些基础研究人员为“核心科学家”。
1 相关工作
目前社会关系网络研究中最受关注的,除了基于论文合作的社会关系网络外,国外的主要有基于关注关系的Twitter,类似于国内的微博。国内已有的基础研究人员社会关系网络主要基于论文合作关系的信息服务平台,具有代表性系统包括深圳爱瑞斯公司研发的科研之友、清华大学知识工程库研发的ArnetMiner[9]系统、仅限于计算机领域合作关系的CCF学术空间[10]、中国人民大学数据库组研发的学术空间[11]、基于论文引用的社会关系网络[12],此外,还有基于电话的社会关系网络[8]。文献[31]提出了基于项目合作社会关系网络的构建问题,并对这个问题进行了研究,提出了实体识别算法等。目前对于社会关系网络的研究大概可以分成以下三个方面:
1) 社会影响分析与行为分析。Sun等[13]探讨网络上顶点与边的影响力分析、节点与边的度量关系。文献[14]讨论大规模网络上的合群性问题,提出了一个分布式机器学习算法构建概论模型来预测用户的行为。文献[15]研究了社会关系网络中强连接顶点问题。文献[16]重构人与人之间信息传播途径来模拟大规模互联网分发连锁信的传播机制,发现连锁信通过一种像树一样的很窄很深模式传播途径。Myers等[17]研究了消息的扩散过程是如何受外来消息源的影响。文献[18]提出了一个半监督(semi-supervise)学习框架来预测用户转发行为(Twitter)。文献[26]研究了社会关系网络的用户转发行为(weibo)。文献[19]提出了一种按照主题分类的作者影响力分析方法。
2) 社会关系分析。文献[21]研究了异构网络环境下如何区分不同类型的社会关系。文献[22]以论文合作的社会关系为基础,能够从论文合作关系中挖掘出导师与学生关系。文献[23]提出了监督随机游走(random walk)算法来评估顶点间的强度。文献[24]提出了移动通话数据中的几种关系模式,并利用这些模式来推断朋友关系网络。文献[25]研究了多个类型动态网络中社区演化。
3) 社会网络结构分析。文献[27]等发现社会关系网络的局部性,即个体容易受到其周围朋友影响,利用这个局部性来预测用户的转发行为。文献[20]研究了社会关系网络中Triad形成,并讨论其在信息传播过程中的作用。文献[28]提出的结构洞(structuralholes)理论在社会系网络结构分析得到了实践与应用。文献[29]研究了社会关系网络的结构洞形成问题。文献[30]等形式化描述了大型社会关系网络的结构洞问题,利用网络最大流最小割来挖掘结构洞令人印象深刻。与本文关系最密切的是文献[7],作者分别提出了贪心算法与weba算法,其贪心算法不断从全局中选取度数最大的顶点直到满足条件为止,weba算法是在贪心算法的基础上做的改进。
2 问题定义
先给出一些基本的定义:一个社会关系网络可以用一个图G(V,E)来表示,V表示顶点集合,E⊆V×V是边的集合,|E|=m表示边的数量,|V|=n表示顶点的数量。同时给出如下的重要定义:
定义1[核心社团]给定一个图G(V,E),e个互不相交的子集合{K1,K2,…,Ke}是核心社团,如果满足以下条件:
1) |E(u,Ki)|≥|E(v,Ki)|;
2) |E(Ki,u)|≥|E(Ki,v)|,这里的E(A,B)={(u,v)|u∈A,v∈B},A,B⊆V。
其中:∀i,∀u∈Ki,∀v∉Ki。
核心社团在图上表现出来的特点就是社团内部关系比较紧密,而社团外的顶点与社团关系比较稀疏,这种稀疏关系从二个方向进或者出核心社团都是如此。
定义2[辅助社团]给定一个图G(V,E),e个子集合{AK1,AK2,…,AKe}是辅助社团,如果满足以下条件:
1) ∀i∈{1,2,…,e},AKi∩Ki=Ø
2) ∀i,∀j≠i,u∈AKi,|E(u,Ki)|≥|E(u,Kj)|
3) ∀i∈{1,2,…,e},|E(AKi,Ki)|≥|E(Ki,Ki)|
这里的Ki是核心社团。
一个核心社团与辅助社团是不相交的,辅助社团与其对应的核心社团之间关系比较紧致,而且辅助社团之间的关系不如其与核心社团紧致。在项目合作的社会关系网络中,核心社团里的科学家互相之间关系是最紧的,辅助社团里科学家与其核心社团关系要比辅助社团之间紧致,一般而言,核心社团里面科学家大多是资深科学家,而辅助社团里面则是一些同课题组的年轻科学家。考虑到可能“核心科学家”同时出现在二个核心社团中,这里的核心社团Ki与Kj可以有相交的,不要求Ki∩Kj=Ø,i≠j。辅助社团AKi与AKj也可以有相交的,不要求AKi∩AKj=Ø,i≠j。
基于以上这些定义与观察,我们可以给出本文的问题定义。
定义3[问题定义]给定一个图G(V,E),问题是如何在可以接受的时间内找出核心社团与辅助社团。
定义3中给出问题已经被证明是NP-hard问题[32]。
3 基于贪心的挖掘算法
3.1 评价指标
提出评价发现的社团好坏的指标,主要是考察其致密程度的四个指标:s0、s1、s2、s3,其定义分别如下:
定义4[紧致匹配]设顶点a在结果集Ci中,如果其邻居节点b也在Ci中,边(a,b)称为一个紧致匹配。
s0是c2与c1的比值。c1是Ci中所有紧致匹配的数量,(a,b)同时有可能同样地出现在测试数据集Bi中,其紧致匹配的数量记为c2。
s1与s0正好是反向计算,设顶点a在结果集Bi中,如果其临接节点b也在Bi中,n1是Bi中所有紧致匹配的数量,(a,b)同时有可能同样地出现在测试数据集Ci中,其紧致匹配的数量记为n2。
指标s2是衡量二分类模型精确度的一种指标:
指标s3为计算结果集合Ci与测试基准数据Bi的交集与并集的比值,表示结果集覆盖了测试基准集的比例:
本文采用s0、s1、s2、s3这四个指标来评价社团发现结果的好坏。
3.2 主要算法
算法的总框架如下所示。输入图G(V,E)和社团大小k,输出e个核心社团。算法开始设置社团为空,参数fmax是最小的整数。整个过程需要多次迭代,每次迭代都选择一个顶点v加入S,v的度数需要满足一定要求。当S小于k时,调用贪心算法使得S中的元素数量等于k,然后计算本轮迭代的效果。如果比前面的结果好,那么更新这个结果,本轮的迭代结果以前没有过,加入到最后的结果集中。
Input:G(V,E), 社团大小k
Output: 核心社团K={K1,K2,…,Ke}
1.K←Ø,fmax=-INT_MAX
2. For step=0 to maxstep
3. S←chooseυ∈V
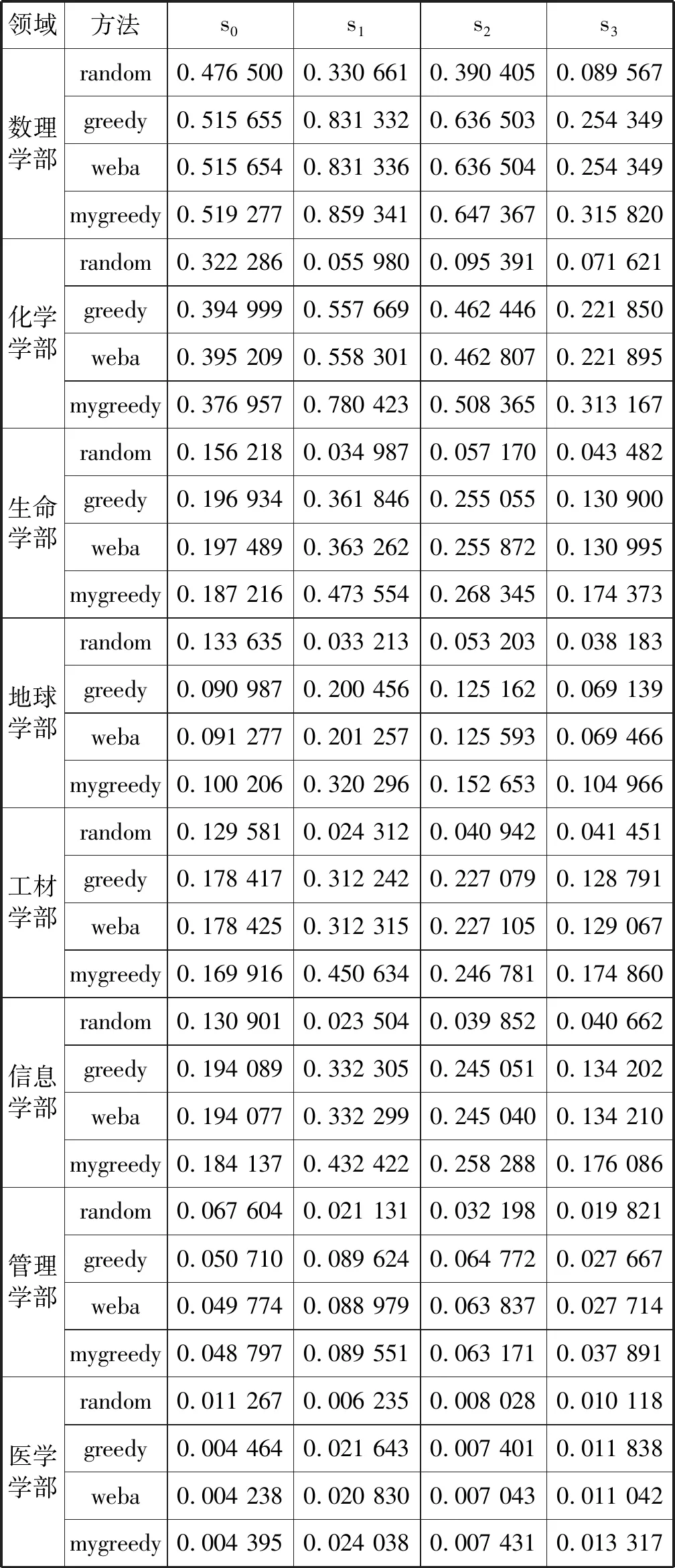
4. while |S| 5. call greedy _algorithm(v,k,V) 6. calculate its evaluationf 7. if (f>fmax) then 8.fmax=f 9.Smax=S 10. if (S∉K) thenK={K,Smax} 11. return K 影响算法结果的关键步骤是第3步与第5步。选择第一个顶点v加入到S与本次迭代的结果有重要的影响,考虑到本文的图结构存在孤立点(度数是0),如果第一个顶点v是孤立的点,则本次的循环不起作用,因此第一个选入的顶点不能是孤立的顶点,而且要保证每次选择的点不同。 贪心算法的启发式策略是根据s0与s1的定义:顶点a如果加入到结果集,最好将其邻居顶点中度数最大的顶点b也加入结果集,如此可以增加紧致匹配c2(n1)的数量,从而提高社团的紧密度。根据此策略:第一步把节点v的所有邻居节点N(v)都加入候选集合CS中,只要S小于k个节点,从CS集合中挑出度数最大的节点vv加入S,接着把vv的邻居节点加入CS集,一直循环直到S满足条件为止。 greedy_algorithm Input:G(V,E) 社团大小k,ν Output:S 1. addN(v) toCS 2. while |S| 3. pick the max degree nodevvtoSfromCS 4. Add theN(vv) adjacent node to candidat setCS 5. returnS 一次迭代算法运行时间不超过O(n+m),因此整个算法过程时间复杂度依然是O(n+m)。本算法与文献[7]中提出贪心算法是有区别的,文献[7]一直在选取全图中最大度数的顶点加入到结果集中,实验结果表明其贪心策略导致结果不一定最优。考虑到其致密指标的定义,上述算法要求加入的顶点必须出现在已有结果集的邻居顶点上,不一定是全图最大度数顶点。 用于测试的数据集是国家基金委每年申请书中提取的合作关系的9 840 477条数据,其中含有男性和女性数据各有6 092 060和3 748 417条。每条元组7个属性(项目编号,姓名,单位,邮箱,性别,是否主持人,唯一身份标记码),相同的申请人赋予一个相同的ID号,同时去除所有的学生,最后整理出来一个基于项目合作社会关系网络,有1 173 788个顶点,每个顶点代表了一个科学家,4 627 413条边,每条边表示一种合作关系[31]。根据项目的受理编号,将所有的申请人与参与人分到8个学部。这些数据作为测试算法准确性的测试基准数据B={B1,B2,…,B8},算法计算出的结果集记为C={C1,C2,…,C8}。 所有程序用C++实现,在IntelCore(TM) i7-6500CPU 2.5 GHz,8 GB内存上运行,将本文算法(标记为mygreedy)与随机算法(标记为random)、Weba算法(标记为weba[7])、greedy算法(标记为greedy[7])等相比较,结果如表1所示。迭代次数maxstep设为1 000次。 表1 四种算法对比结果 从计算结果上看,本文方法在主要指标s2与s3上比其他几种算法略胜一筹,random算法在大部分情况下是最差的,其次是greedy算法和weba算法。weba是在greedy算法基础上做的改进,从实验结果来看,改进效果并不明显,相反在某些情况反而降低了其结果。从学部来看,数理学部的结果是最好的,这是由于数理学部成立时间最久,申请人与参与人的信息最完备,关系网络较完整,联系较强,而医学部则是在2009年成立的,数据截止到2014年,数据量明显偏少,而且社会关系网络结构较弱。 从计算指标上看,所有的算法都突出s2,而s2是由s0与s1加权结果,结果中出现s0表现较好,s2反而不好的现象,这是由于算法迭代更新的时候只比较了s2。在管理学部,weba算法在指标s2上表现得比mygreedy算法好,其余都不如mygreedy算法,且在信息学部与管理学部,weba算法不如greedy算法。当合作关系比较密,本文算法效果较好(数理学部),当关系比较稀疏,本文算法效果与文献[7]不相上下。 从运行时间来看,random算法用时超过48个小时,其余算法用时都在6个小时内,没有太多的比较意义,故省略。 本文通过将基金项目申请合作关系作为一种特定结构的社会关系网络,并有针对性地设计算法,为发现基础研究中的核心社团-核心科学家提供一种新的方法。该方法和结果对制定基金资助战略布局和引导政策有一定的参考意义。4 实 验
5 结 语
