矩阵最大线性无关子块提取研究
2020-03-12王芳马艳丽
王芳,马艳丽
(1.安徽外国语学院 公共基础课教学部,安徽 合肥 231200;2.安徽新华学院 通识教育部,安徽 合肥 230088)
对于求解大型稀疏线性方程组Ax=b,其中A∈Rm×m,x,b∈m×1.文[1]中有以下结论:
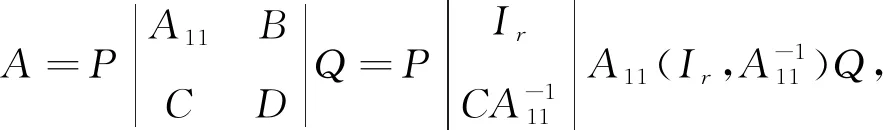
其中,rank(A)=r,A11是矩阵A的一个最大线性无关子块,P、Q为相应的置换矩阵,R是任意一个r阶的非奇异矩阵.可知,得到M+的关键在于提取矩阵A的一个最大线性无关子块A11,本文将给出提取A11及相应的置换矩阵P、Q的算法.
1 相关定义及引理
定义1 若矩阵A的秩为r,则A必有一个非奇异的子矩阵A11∈Rr×r,称A11为矩阵A的最大线性无关子块.
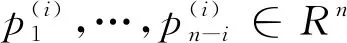

2 提取A11及相应置换矩阵P,Q的算法
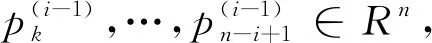
则
故
是齐次线性方程组Λix=0的一个解.其中
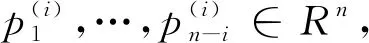



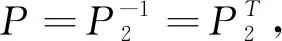
算法1:
(1)size(A)=[m,n],置初始量:m阶单位矩阵Im×m,n阶单位矩阵In×n,l=2,k=1,s=[1];
(2)若a11=0,aij≠0,则将Im×m第一行与第i行互换,In×n的第一列与第j列互换,并将互换后的矩阵记作P1与Q1,令A=P1AQ1;


算法2:

(2)置初始量:m阶单位矩阵Im×m,n阶单位矩阵In×n;

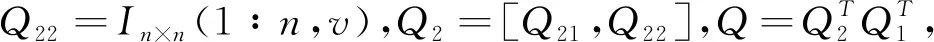
3 数值实验
以下数值实验均在Intel(R) Core(TM) i5-8265U CPU@1.60GHz 1.80GHz内存为8.00 GB的个人计算机上完成,所用软件为MATLAB R2018a,矩阵来自“Matrix Market”,皆为实数矩阵.取初始向量x0=0,停机准则为:
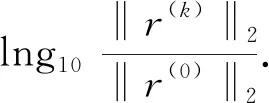
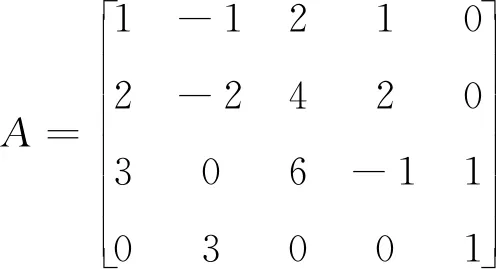


数值实验2 使用算法2提取以下矩阵的最大线性无关子块,其中ε取1.0×10-10,t表示算法2运行时间(单位为秒),运算结果见表1..

表1 算法2的运行时间(单位为秒)
数值实验3(见文献[3]) 对于泊松方程
考虑周期边界条件u(x,0)=u(x,1),u(0,y)=u(1,y),则矩阵A是如下矩阵,其中h=1/m,n=m2,α±=1±dh/2,取m=64,d=10,即得A是4 096×4 096阶矩阵.

rank(BBT)=1,rank(CTC)=1,


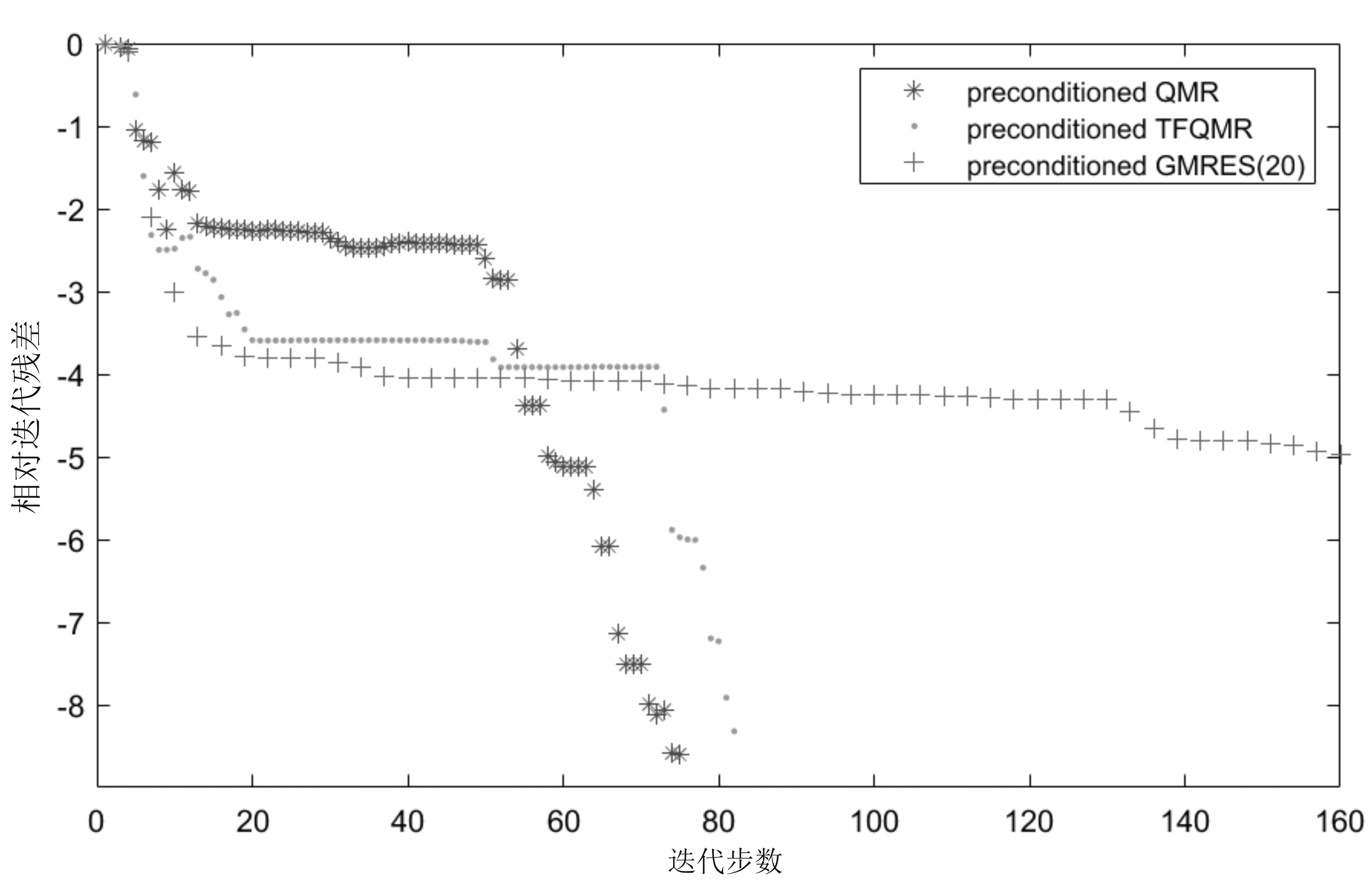
图1 数值实验2的收敛图像
4 小 结
综上所述,预条件QMR算法与预条件TFQMR算法,预条件GMRES算法是高效的,对于提取大型稀疏矩阵的最大线性无关子块A11,算法中ε的取值,对算法有一定的影响.构造基于恰当分裂的预条件子时,如果需要提取最大线性无关子块A11,代价也是昂贵的.
