基于改进鲸鱼算法考虑尾流效应的风电场优化控制

陈 景，樊小朝，史瑞静，王维庆，李鉴博

(可再生能源发电与并网技术教育部工程研究中心(新疆大学)，新疆乌鲁木齐830047)

0 引 言

据统计，截至2019年底我国风电累计并网容量已达2.1亿kW，年发电量为4 057亿kW·h[1]。随着风电的迅速发展，风电场内风电机组容量与排列密度的持续增加，尾流效应对风电场功率输出影响日益突出。研究数据显示，综合考虑各种风向情况下陆上风电场尾流效应损失能量为12%，海上风电场尾流效应损失能量为8%[2-3]。

现有风电场多采用最大风能追踪策略来控制风电机组功率输出[4-5]，该策略仅考虑单台风电机组最大功率追踪，忽略了尾流效应影响，将导致风电场上游风电机组捕获风能过多，下游机组风速损失较大，使得风电场整体输出功率并非最大。而采用控制风电场内风电机组运行状态来降低尾流影响，提升风电场整体输出功率成为当前研究热点之一。但考虑尾流效应的风电场功率输出控制模型往往具有维数高，非线性和耦合参数多的特点[6]，为此，探寻适合的风电场优化控制方法显得尤为重要。文献[7]提出一种考虑尾流影响时抑制优化方程计算规模的海上风电场有功功率输出优化方法。文献[8]考虑尾流影响时提出一种采用内点法调节各风电机组轴向诱导因子来协调优化机组有功功率输出控制方法。文献[9]为减小风电机组间尾流影响，提出一种采用遗传算法优化相关控制变量的集群优化控制策略。文献[10]针对已建大型风电场，提出一种考虑尾流效应时以轴向诱导因子为优化变量，粒子群算法为优化算法的风电场优化控制方法，可有效提高风电场整体输出功率，但由于优化变量维数高，耦合参数多的原因，并未得到最优解。

本文针对考虑尾流效应的风电场优化控制模型具有维数高，非线性，耦合参数多的特点，引入一种适用于解决大规模复杂问题的鲸鱼优化(Whale Optimization Algorithm，WOA)算法[11]。对算法本身存在迭代后期收敛速度慢，最优个体局部聚集问题提出改进，并通过仿真对比5种算法计算考虑尾流效应的风电场功率输出最优解，所得结果验证了其应用于该领域的可行性与有效性。

1 尾流模型与风电场功率输出控制模型

1.1 尾流模型

文中选择Jensen尾流模型对风电场进行尾流模拟，该模型主要适用于平坦地形风电场，公式为

rw=r+ks

(1)

(2)

式中，k为尾流衰减系数，依据Barthlmie等[3]建议，陆上k可取0.075，海上k可取0.04；r为风电机组风轮半径；rw为风电机组下游s远处尾流半径；vw为风电机组下游s远处尾流风速；v0为无穷远处来流风速；CT为风电机组推力系数。

在大型风电场中，由于风电机组数量较多，来流风向下游风电机组可能受到上游多台风电机组尾流影响而形成尾流叠加情况。上游风电机组尾流对下游风电机组的影响可分为三种：无影响，部分覆盖，全覆盖，其中部分覆盖时根据覆盖的面积可分为图1两种情况。

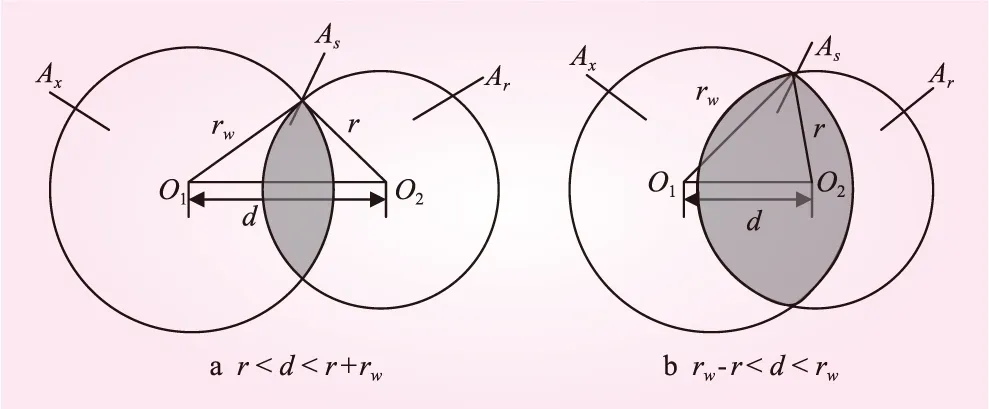
图1 尾流覆盖风轮区域

图1中，Ax为上游风电机组尾流影响区域，Ar为下游风电机组扫风面积，d为两台风电机组间距离，重合部分表示下游风电机组受上游风电机组尾流影响区域。图1中a，b两种情况的尾流影响区域面积As计算公式为

(3)

基于式(3)与单位时间内气流动量守恒定律可得到风电场内受上游多台风电机组尾流影响的下游风电机组输入风速vi计算公式为

(4)

式中，vj，i为上游第j台风电机组在下游第i台风电机组处尾流风速；vj为假设第j台风电机组不受任何尾流影响时的输入风速。

1.2 风电场功率输出控制模型

已知风电场风电机组输出功率和作用在风电机组上推力公式为

(5)

(6)

式中，ρ为空气密度；CP为风能利用系数。

来流风速经过风轮平面时会损失部分能量使风速降低，定义风轮平面风速与来流风速减少比例为轴向诱导因子a，可由下式表示

(7)

式中，v为风电机组风轮后风速。在满足质量守恒，动量守恒，Bernoulli方程的条件下可推导出推力系数CT和风能利用系数CP的表达式为

(8)

(9)

由式(9)可知，CP对a求导等于0时即为最大风能利用系数值

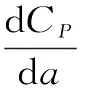
(10)

由式(7)与(10)可以看出，当a=1时,v0=v,无物理意义；a=1/3时，CP取得最大值0.593，即贝兹极限值。最后由式(5)、(8)和(9)可得出风电机组输出功率与推力系数的关系为

(11)

2 改进鲸鱼优化算法

2.1 基本鲸鱼优化算法(WOA)

鲸鱼优化算法是Mirjalilis在2016年模仿大海中鲸鱼觅食行为实现的一种仿生类智能优化算法[12]。该算法优化过程主要包括三个阶段：即环绕捕食，气泡网袭击和食物搜寻阶段。

2.1.1环绕捕食阶段

鲸鱼在捕食时可识别猎物位置并环绕游行，算法设定当前最优或接近最优候选解为捕食目标，其他鲸鱼均向最优鲸鱼方向更新位置。该环绕捕食行为的数学表达式为

(12)

(13)

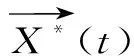
(14)

(15)

a(t)=2-2t/tmax

(16)

式中，tmax为最大迭代次数。

2.1.2气泡袭击阶段

鲸鱼通过螺旋环绕和缩小包围圈的方式靠近猎物，同时吐气泡将猎物包围其中，公式为

(17)

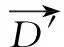
为模拟螺旋环绕的同时收缩包围游向猎物的行为，建立如下位置更新公式

(18)

式中，p为[0，1]间随机数。随机值p的大小决定鲸鱼进行螺旋环绕或收缩包围运动。

2.1.3食物搜寻阶段

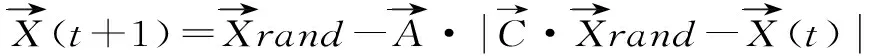
(19)

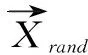
2.2 鲸鱼优化算法改进(IWOA)

2.2.1基于立方混沌映射的种群初始化

对于基于种群迭代的智能算法来说，种群的质量直接影响算法的搜索进程，文献[13]通过数学推理证明了立方混沌映射要比Logistic混沌映射具有更好的历遍均匀性。立方映射表达式为

(20)

假设需要初始化的种群有D维个体，先随机产生一个在[-1，1]的向量作为初始个体，再用上式(20)进行D-1次迭代，再利用下式(21)将立方混沌映射产生的在[-1，1]上的变量映射到解区间[xl，xh]上。

(21)

式中,xl,xh为解的区间上下限；y′为由式(20)产生的混沌变量；x′为在解区间上映射后的混沌变量。

2.2.2改进非线性收敛因子

(22)

式中，ai、af分别为收敛因子起始和结束值；α>0、β>0，为非线性调节参数，通过调节α、β值可控制算法迭代前期与后期收敛因子值。

2.2.3改进混合蛙跳算法最差蛙位置改变策略

在WOA算法中，随着迭代次数增加，群体中所有个体都逐步向最优个体局部聚集，导致群体多样性减少，易使算法陷入局部最优。为解决这一问题，受SFLA算法[14]启发引入一种最差蛙位置改变策略，公式为

(23)

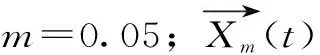
3 基于改进鲸鱼算法的风电场优化控制

风电场内所有风电机组均工作在单机最大风能捕获状态，并不能保证风电场整体输出功率最大，为此，文中通过调节风电场内各个风电机组运行状态来提高风电场整体功率输出。

3.1 优化控制目标函数与约束条件

改进鲸鱼算法的优化目标为风电场内所有风电机组输出功率之和最大，控制变量为风电机组推力系数CT，则文中优化控制的目标函数与约束条件为

(24)

式中，Ptotal为整体风电场输出功率；N为风电机组数量；vi为第i台风电机组处风速；Pi为第i台风电机组输出功率；Prate为风电机组额定功率；CT，i为第i台风电机组推力系数。

3.2 IWOA算法优化控制流程

IWOA算法首先通过立体混沌映射提高了种群多样性，然后通过非收敛因子和改进混合蛙跳算法中最差蛙位置改变策略协调了算法局部开发与全局探索能力，其在考虑尾流效应的风电场优化控制过程如图2所示。

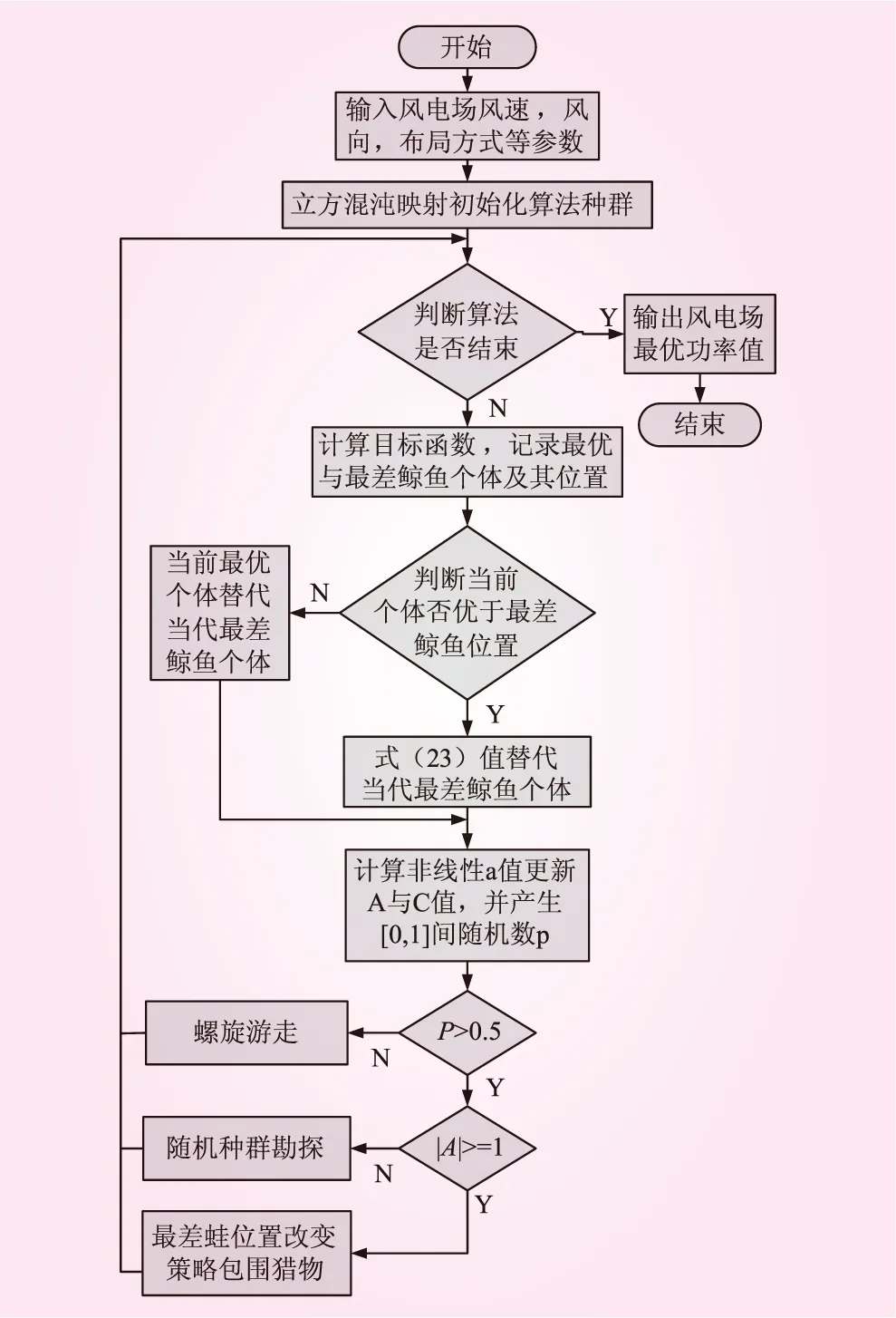
图2 改进鲸鱼优化算法控制流程

4 算例分析

为验证所提算法有效性，使用MATLAB软件对由1.5 MW双馈异步风电机组组成的风电场进行仿真分析。为便于分析不妨设风电场内所有风机按规则方式排列，风电机组排列方式如图3所示。

图3 风电场风电机组布局示意

设定风电场内相邻两台风电机组水平与垂直间距均为300 m，叶片半径为31.5 m，风轮中心点高度为70 m，风电机组切入风速为3 m/s，额定风速为13 m/s。统一设置各算法种群规模为300，迭代次数为400，对风向0°，风速10 m/s时风电场内风电机组行数m列数n均为10时进行仿真分析，所用计算机处理器为Core(TM)i5-3210M。

图4为风电场内风电机组行数m列数n均为10时采用不同算法计算的功率对比图。图中虚线为采用单机最大功率追踪策略求出的风电场整体输出功率，值为68.52 MW。实线为采用不同算法计算得到的风电场整体输出功率值，其中GA算法耗时31.8 s，计算所得输出功率为73.57 MW，PSO算法耗时19.1 s，输出功率为74.32 MW，GWO算法耗时21.2 s，输出功率为75.15 MW，WOA算法耗时17.4 s，输出功率为75.22 MW，IWOA算法耗时17.5 s，输出功率为75.89 MW。可以看出，采用算法优化时风电场输出功率要明显高于优化之前，但由于求解空间维数高，耦合参数多的原因，GA算法计算结果波动较大且难以求出最优值，PSO算法计算时间较短收敛速度较快但易陷入局部解，GWO算法收敛速度差且易陷入局部解。而IWOA算法可以克服以上缺点，所求输出功率相对单机最大功率追踪策略提高了10.76%，在大规模高维数复杂问题方面表现较好，证明本文所提算法的可行性与有效性。

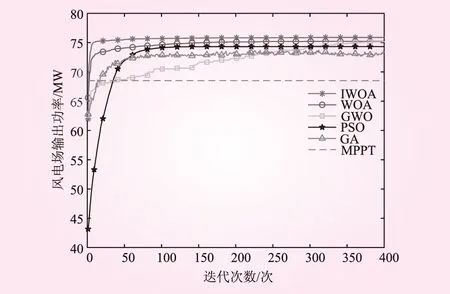
图4 风电机组行列数均为10时算法对比

图5与图6为风电场内风电机组行数m列数n均为10时采用最大功率追踪和IWOA算法优化的风电场输出功率分布图，从图中可以看出，采用单机最大功率追踪策略时风电场内上游风电机组捕获风能较多导致下游风电机组出力跌落较大，而IWOA算法则通过控制风电机组推力系数降低上游部分风电机组的风能利用率来增大尾流区域风速，从而实现风电场整体功率输出最大。

图5 单机最大功率追踪时功率分布

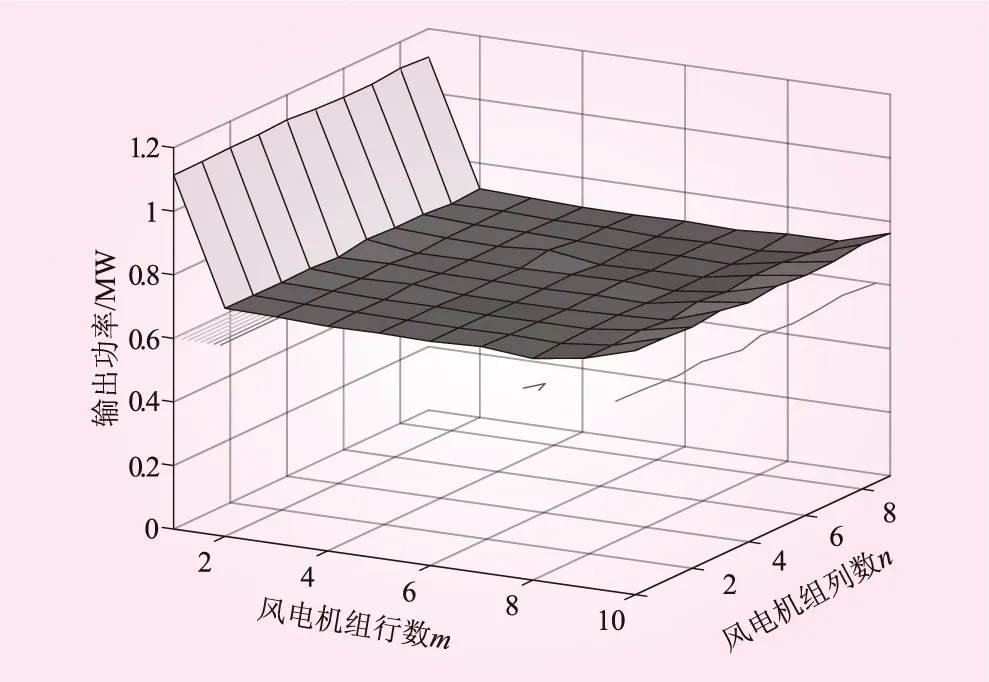
图6 IWOA算法优化时功率分布

5 结 论

对于考虑尾流效应的风电场功率输出控制模型存在高维数，非线性，耦合参数多问题，提出一种适用于解决大规模复杂问题的改进鲸鱼优化算法来求解此问题，具体内容包括：

(1)采用立方混沌映射种群初始化方法提高算法种群质量，提出一种新的非线性收敛因子公式来协调算法全局探索与局部开发能力，引入改进混合蛙跳算法中一种最差蛙位置改变策略增强算法全局搜索能力。

(2)通过仿真对比5种算法计算风电场功率输出最优解，结果表明：IWOA算法的收敛速度，精度都比其他算法表现要好，证明了本文所提算法在考虑尾流效应的风电场功率输出优化控制方面的可行性与有效性。