基于降雨规律的流域水库群消落调度函数研究

王二朋，赵云发，李 鹏，曹 辉，张 俊

(1.中国长江电力股份有限公司三峡水利枢纽梯级调度通信中心，湖北宜昌443433；2.中国长江电力股份有限公司智慧长江与水电科学湖北省重点实验室，湖北宜昌443000)

0 引言

随着各流域大型水库群的相继建成，水库的汛前消落格局发生了深刻变化，如果各水库仅考虑自身效益而进行无序消落，将可能导致其他水库汛前弃水，整个梯级产生人造洪峰等不利现象。探寻水库群联合消落调度模型和调度函数，可指导大流域水库群有序消落，提高水能利用率，兼顾局部效益并达到整体效益最大化。

目前水库优化调度模型已经解决了径流已知前提下的优化调度问题，然而大多数模型难以直接指导径流未知情况下的水库实际运行。但是这种长系列优化调度成果隐藏了丰富的调度运行信息，通过挖掘其中决策变量(如水位、出力)与相关因子(如时段入库、初水位)之间的内在隐含联系，采用函数的形式进行表征，可以达到指导水库运行调度的目的。现有的调度函数研究主要针对整个水文年的单库或梯级水库调度[1-5]，对于大流域水库群的联合优化调度函数研究较少，针对大流域水库群消落期调度函数的研究更少。

本文在调度模型构建上适当简化。在空间上，针对水库数量的增加，各库之间水文联系复杂的特点，对同一支流水库群采用聚合虚拟水库形式进行简化；在时间上，针对消落期调度在全年调度过程中目标性强的特点，将单库优化过程简化为寻求消落至死水位的最优时间，将全流域水库群优化过程简化为寻求不同子流域水库群消落至最少可用水量的优先次序。

在函数的构建方面，通过分析水库群消落期调度机理、气象统计规律、结合调度实践经验，引进了子流域雨季开始时间和首场强降雨时间两个相关因子。根据消落期调度特点选取水位作为决策变量，建立大流域水库群的联合消落调度函数。从长系列的水库群优化调度样本中获取决策规律，率定待定参数。最后，结合前期总结规律和中长期气象预报信息，达到指导各个水库消落调度并提高全流域水库群综合效益的目的。

1 相关因子和决策变量的选取

1.1 相关因子选取依据

我国大多数流域径流补给以大气降水为主，流域面雨量与同期径流在消落期有很显著相关关系[6-8]，而径流是影响水库群消落的主要因素。因此，流域降雨规律对流域水库群的消落规影响巨大。

受到季风性气候的影响，我国大部分地区降水量东多西少的空间分布特征明显，雨带随时间变化在空间上逐步推进规律显著。以长江流域为例，主消落期等雨量线呈东南-西北走向，降水量从流域东南向西北迅速递减，雨季开始时间和首场强降雨时间从下游往上游逐步延后。

选择各子流域雨季开始时间和首场强降雨时间其作为相关因子主要原因如下：

(1)两个因子反映了流域降雨时间分布特征和径流丰枯交替变化规律，从水库消落调度角度是水位消落至较低水位和开始回蓄的一个重要参考。

(2)同一子流域水库群中各水库对应的气象特征时间相同，因此可以减少函数表达式中的参数个数，可以适用大流域大尺度的调度函数构造。

(3)相对于其它常用因子(入库流量与初水位乘积、初水位平方等)[9]，物理含义明确，能够从调度机理层面反映其与决策变量之间的关系。

(4)根据目前的气象技术手段采用最优子集法可以预测子流域雨季开始时间和首场强降雨时间，精度符合调度需求，可以指导后期消落。

1.2 相关因子的计算方法

1.2.1雨季开始

雨季开始时间的确定：从第1个雨日算起，往后2、3日、…、10日中雨日数占相应时段内总日数的比例≥50%，则第一个雨日为雨季开始日。

受大气环流影响，各流域每年雨季开始变化较大。受地形和地理位置影响，同一流域各水文分区雨季开始时间也不尽相同。为了方便研究，雨季开始的临界值R0按以下公式计算[10]:

(1)

式中，K为系数，取值范围为1.0～1.5；Rij为第j年第i天的面雨量；N为统计的年份数。在同一年份中，凡连续10d滑动面雨量合计大于该临界值的初始日，则统计为该流域当年雨季开始日。

1961年～2018年长江上游流域雨季开始时间计算和统计成果见表1。

表1 1961年～2018年长江上游流域雨季开始日期统计

1.2.2首场强降雨

考虑到日界线的影响，将连续2天平均累积降水量和单日平均降水量作为研究对象，采用累积频率方法，经多次调试，确定各子流域累积频率达到95%时，所对应的连续两天平均累积降水量临界值定义为强降水的阈值，各子流域连续两天平均累积降水量超过该阈值时确定为强降水过程。

1961年～2018年长江上游流域首场强降雨日期统计成果见表2。

表2 1961年～2018年长江上游首场强降雨日期统计

1.3 决策变量的选取

常用的决策变量包括：时段平均出库流量(水量)、时段平均出力、时段末蓄水量或时段末水位。为了能更显著反映消落期水库运行要素与水库决策属性之间的关系，结合调度人员在水库实际消落调度过程中的需求，采用水库时段末水位作为决策变量。

2 水库群联合消落调度模型

2.1 模型建立

为获取发电量最大条件下的联合消落调度函数，现建立流域水库群消落期确定性优化发电最大模型：

2.1.1数学描述

给定消落调度期内水库群各水电站入库径流过程、水库初水位(设定为正常蓄水位)、最低消落水位(设定为死水位)、末水位(一般设定为汛限水位)、出力约束范围(考虑非汛期负荷率)、其他约束(航运、补水最小下泄)。综合考虑各种约束条件，确定梯级各水库水位变化过程，使调度期内的发电量最大，并适当考虑避免弃水损失。消落调度目标函数为

(2)

式中，m、t分别为电站序号和时段序号；M、T分别为梯级电站总数和时段总数；E(m， t)为第m级电站、第t时段发电量；Δt为调度时段长度。

2.1.2模型简化

针对单个或者较少数量水库的消落调度，理论上最优方案为汛前保持高水位，丰枯交替时集中快速消落至汛限水位。而流域水库群联合消落调度，需要考虑水量和电力的补偿、共用外送通道、分时段电价、流域径流特性、水库水电站运行特点、库岸稳定、流域防洪等需求。

经过模拟测算表明，在合适的时间均匀消落至死水位然后均匀回蓄(如图1)，才能充分发挥水电站群的经济效益和社会效益。主要原因如下：对于自身，一方面可以充分利用水库的调节库容增加枯水期发电量，另一方面可以充分利用水资源减少汛期弃水；对于同一梯级径流式电站，可以增加枯水期发电流量，减轻雨季到来后通道竞争和弃水压力；对于下游干流控制性水库，可以提高其枯期水头效益，减轻雨季到来后下游地区防洪压力。

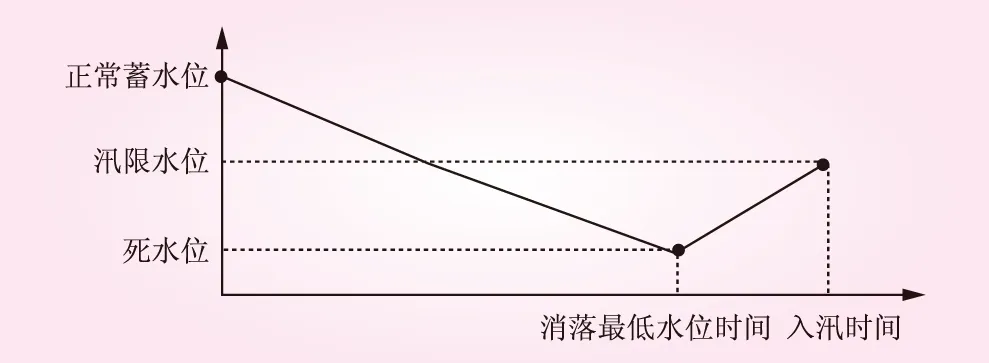
图1 单个水库消落调度规则简化示意

近年的调度实践也表明，大多数大型控制性水库在制作消落计划和实际调度中采用这种消落方式。

针对大流域水库群，随着水库数量和考虑信息种类的增多计算维数逐渐增加，使得维数灾问题更加突出。为了有效降维，根据水文或地理特征将每一个子流域梯级水库聚合为一个虚拟水库。该虚拟水库内所有水库处于同一降雨分区，其入库径流变化规律相同，设定具有相同的消落节奏(相对消落深度保持一致)，虚拟水库的调度规则即为子流域内各水库调度规则。

2.2 模型求解

同一子流域梯级水库中各个水库电站参数不同，边界条件不同。不同子流域的虚拟水库与干流控制性水库组成复杂的混联水库群。目前对于这种大流域水库联合优化没有有效的算法，因此只能采用逐步试算法，求得模型近似最优解。

计算步骤：①选取任一子流域，结合该流域梯级水库历史实际消落到死水位时间段，向前后延伸1～2旬。该范围作为可供试错选择的时间区间(以旬为尺度进行离散)。②每一个离散点作为消落至死水位时间对应一种消落方案。根据消落水量和回蓄水量的时间分配确定出库流量，结合天然旬均入库流量、各个电站的参数和限制计算不同消落方案的发电量和弃水量。③同一子流域的各个电站计算结果作为一个整体，以发电量之和最大为第一标准，弃水量最小为第二标准(发电量相差1%以内，启用该标准)选出调度效果最优的四种方案，作为该子流域的优选方案。④将每个子流域的四种最优方案进行排列组合，采用同样的标准选出全流域调度效果最优的方案作为全流域旬尺度的近似最优消落方案。⑤在旬尺度最优结果对应的消落至死水位时间的基础上向前后延伸1候，重复以上计算，寻求候尺度最优解，可近似作为最优解。⑥逐年进行以上计算，可得到每年全流域近似最优解。

3 调度函数的构建

3.1 调度函数形式的确定

根据以上分析并结合选取的相关因子确定流域水库群消落函数为

(3)

上式虽然表述了水库群决策性与水库初水位状态、面临时段来水之间的关系，但尚不清楚调度函数g(·)应采取何种函数形式才能准确表达其中隐藏的规律。大量研究表明[9]在一定范围内任意光滑非线性函数可以用线性函数来近似描述。可将调度函数中非线性部分简化为线性函数

Ti=aRi+bSi+cWi+d

(4)

式中，a、b、c、d为待识别参数。如果流域水库群有n个子流域，则a、b、c的结果为n×n矩阵，d为n维向量。

3.2 调度函数参数的拟合

获取k年的长序列实测径流资料，通过求解水库群联合优化调度模型得到确定性优化计算成果，即k组样本。一般不存在常数a、b、c、d使得式4严格成立，称Ti=(aRi+bSi+cWi+d)为残差。记θ为待求参数矩阵，记X和Y分别为相关因子和决策变量的观测数据矩阵，则θ=(XTX)-1XTY。

由于水库群联合补偿机制作用，各子流域水库群消落策略不仅取决于自身消落状态以及来水，而且与其余子流域相应时段状态变量相关。不同流域水库群电站群指标不同，径流气候特征不同。因此，调度函数与各因子的相关性是不同的，自变量对决策变量的贡献程度不相同。需要采用逐步分析法计算各因子的方差贡献(偏回归平方和)以衡量其重要性，即对该因子进行F检验，如

(5)

式中，P为当前因子个数；Qi为残差平方和；V为方差。给定置信区间α，若Fi>Fα，表明该变量显著，则引入这一因子，否则剔除该因子。

3.3 调度函数相关因子的预测

通过与前期海温场做相关分析，前一年秋季指数、前一年冬季指数、当年春季指数与当年雨季开始时间和首场强降雨开始时间相关显著。采用最优子集回归方法，基于国家气候中心提供的74项环流指数和自定义指数，可以对雨季开始时间和首场强降雨时间进行预测。

考虑到降雨预报存在一定误差，调度函数中Ri和Si的取值将受到影响，但是随着预见期缩短，预报精度将逐步提高。水库消落是一个长期的过程，只要及时滚动更新调度函数，将不会影响其应用效果。实践表明目前预报成果精度可以满足调度需求，可用于提前编制消落计划和实时指导后期调度。

4 实例研究

以长江上游水库群为研究实例，选取2018年已建的长江上游干支流调节库容在1亿m3以上且需要年度消落的主要的控制性水库。包括金沙江中下游的梨园、阿海、金安桥、龙开口、鲁地拉、观音岩、溪洛渡、向家坝；雅砻江的锦屏一级、二滩；岷江的紫坪铺、瀑布沟；嘉陵江的宝珠寺、亭子口；乌江的乌江渡、构皮滩、思林、沙沱、彭水；长江干流的三峡等19座水库。

长江上游流域按面雨量分区可划分为金沙江、岷沱江、嘉陵江、乌江等四大区域。根据上文中公式和相关雨量数据计算出1961年～2018年各流域雨季开始时间和首场强降雨开始时间。为了消除已建水库的调蓄影响，基于水量平衡法对19座水库1961年～2018年1月至6月分旬入库流量进行还原得到天然流量。

取1961年～2012年资料为率定期，2013年～2018年为检验期。

4.1 调度函数构建

利用SPSS软件采用逐步回归法对流域水库群发电量最大模型的调度结果样本和因变量计算结果进行拟合分析，对函数和系数进行显著性检验分析。其中，泯沱江子流域相关因子首次强降雨时间和乌江子流域相关因子雨季开始时间未通过置信度95%的F检验被剔除。确定函数系数后，构建调度函数为

(6)

子流域编号1～5分别为金中、雅砻江、泯沱江、嘉陵江、乌江。其中金中和雅砻江采用同一流域降雨资料。为方便研究，金下干流梯级和长江干流三峡采用目前固定消落方式，不在调度函数中体现。

由于篇幅有限，仅以嘉陵江子流域的亭子口电站为例列出其调度函数如下：

当t<0.372R4+0.165S4+59.09时，Z=20(0.372R4+0.165S4+59.09-t)/(0.372R4+0.165S4+59.09)；当t>0.372R4+0.165S4+59.09时，Z=9(t-0.372R4-0.165S4-59.09)/(t-0.372R4-0.165S4-141.91)。

4.2 调度函数检验

采用水库群检验期(2013年～2018年)逐旬径流资料进行模拟调度，给出实际调度、近似最优调度、调度函数调度方案6年平均值结果如表3所示。

表3 2013年～2018年长江上游水库群优化调度测算结果

从表3可知全流域水库群和各子流域的各项评价指标调度函数方案与优化调度结果接近，相对常规调度方案均有所提高，其中全流域发电量提高约2%(与长系列测算结果均值接近)，弃水损失电量占总电量比例减小20%。各支流中岷沱江流域梯级优化效果一般，雅砻江优化效果最好。

优化结果和调度函数计算结果一致表明，长江上游各支流干流多年优化消落平均次序为：嘉陵江、乌江、泯沱江、雅砻江、金沙江下游、三峡、金沙江中游。基本上与流域降雨特征时间顺序相一致，其中嘉陵江略早于乌江，分析原因可能为统计两流域降雨特征时间接近，而计算中采用的嘉陵江江流域水电站远少于嘉陵江，其权重较小。

在实际调度，可以参考上述消落次序，并结合气象预报和其他约束条件进行修正。

5 结 论

本文构建了水库群联合消落调度模型，近似最优解为样本，采用逐步回归法筛选了与降雨规律相关的影响因子构建了大流域水库群联合消落调度函数。以长江上游流域水库群消落期为例，构造了各子流域水库群消落调度函数，最后采用检验期资料对调度函数进行了验证。结果表明，调度函数能一定程度上提高流域水库群发电效益，减少弃水损失。长江上游各支流优化消落平均次序为：嘉陵江、乌江、泯沱江、雅砻江、金沙江下游、三峡、金沙江中游。

建议建立企业层面大流域联合调度平台，定期发布各子流域中长期降雨预测信息，满足各子流域发电企业制作合理消落调度计划的需求。同时需要系统化研究水库群联合调度补偿机制，制定科学的利益分摊方法，促进流域水资源优化配置。