基于高斯过程回归模型的径流短期预测研究

黄 亚，易 灵，肖伟华，侯贵兵，李媛媛

(1.中水珠江规划勘测设计有限公司，广东广州510610;2.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京100038)

0 引 言

径流预测一直是人们关注的重大问题。传统方法如时间序列法[1]、回归分析法[2]、模糊分析法[3]、小波分析法[4]、集对分析法[5]以及灰色预测法[6]等均在径流预测预报中取得了一定的成效；但是由于河川径流受众多因素的相互作用、相互影响，具有显著的非线性、高维性、混沌性、模糊性等诸多复杂特征，使上述方法的预测精度受到不同程度的影响[7-8]。近年来，一些学者将神经网络(ANN)、支持向量机(SVM)等机器学习方法引入径流预测研究领域，取得了不少有价值的研究成果[9-10]。但是，这些方法本身仍存在着许多公开的问题，如：神经网络存在着最优网络结构难以确定和过度拟合的问题，且单层神经网络收敛速度慢，容易陷入局部极值[11]；SVM计算时间受样本数量影响明显，核函数以及惩罚因子的选取经验性较强，对预测结果影响较大等[12]。为此，探讨新的更为精确径流量预测方法显得日益重要。

高斯过程(Gaussian Processes，GP)作为一种新的机器学习技术在多个领域的应用研究引起了相关学者的密切关注[13-16]。它有严格的统计学理论基础，对处理高维数、小样本、非线性等复杂回归问题具有良好的适应性，而且还具有参数自适应获取和预测结果具有概率意义等优点[17]。GP模型在其他领域已经取得了成功应用。本文以GP模型进行径流预测研究；同时采用传统BP神经网络模型和SVM模型进行参照对比分析，以期寻求更为精确的径流预测方法。

1 GP基本原理及算法的实现

1.1 高斯过程基本原理[18]

假设n个观测数据的训练集为D={(xi，yi|i=1，…，n)}={X,y}。其中，xi为D中的第i个输出变量；yi为D中的第i个目标输出；n为训练集中的样本个数。GP模型是根据先验知识确定输入向量与目标输出之间关系f进行预测的。即在给定输入向量时确定目标输出的条件分布。

假定f为一个高斯过程，即f～GP(m，k)，f是一个以m为均值函数，k为协方差函数的高斯过程。高斯过程是一个随机过程，其与高斯分布类似，高斯过程完全由其均值函数与协方差函数确定。

实际目标输出y往往会包含一些噪声，它与真实输出值f(x)相差ε。即

y=f(x)+ε

(1)

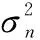
(2)

观测值y的先验分布为

(3)

式中，K=K(X，X)为n×n阶对称正定的协方差矩阵，矩阵中的元素Kij度量了xi和yj的相关程度。

此时，训练数据集的n个训练样本输出向量y和测试数据集的预测值f*构成联合高斯先验分布

(4)

式中，K*=K(X*，X)；K**=K(X*，X*)。二者同样反映了其中元素之间的相关程度。

GP模型可以根据实际预测数据规律选择不同的协方差函数，但都需要满足对任一点集都能够保证产生一个非负正定协方差矩阵[19]。本研究选择各项异性平方指数函数SE作为协方差核函数

(5)

式中，xp、xq分别为训练样本或者测试样本中的任意两个输入向量；σf、l为超参数，可以通过极大似然法获得。即，通过建立训练样本条件概率的对数似然函数对超参数求偏导，再采用共轭梯度优化方法搜索出超参数的最优解。对数自然函数为

(6)

根据式(4)获取最优超参数后，在训练集(X，y)的基础上，再根据贝叶斯原理预测出与X*对应的最大概率的输出值，其中贝叶斯原理采用观测到的真实数据，不断更新概率预测分布，最后在已有训练样本(X，y)和预测样本X*条件下推断出y*的最大概率的预测后验分布

(7)

其预测值y*的均值和方差为

μ*=KT(X*)-K-1y

(8)

(9)

1.2 算法过程的实现

(1)确定训练样本的输入向量Xi中历史点个数p，建立天峨水文站日径流量预测模型的训练样本(X，y)。

(2)数据标准化处理。当天峨水文站径流量实测数据数量级相差较大时或离散性较大时，需对输入、输出数据进行标准化处理。常用的标准化方法是：各训练样本的输入值除以所有样本在各维度上的标准差；对输出进行标准化处理，推荐的标准化方法是对各样本输出减去所有样本输出的平均值。

(3)选择适合的协方差函数，并依据协方差函数对超参数的要求给出初始超参数。

(4)对已建立的天峨水文站径流量训练样本进行训练，并通过对数自然函数式(6)获取最优超参数。

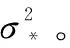
(6)根据上述步骤编制Matlab语言，实现基于GP模型的径流量数据有效预测。

2 工程实例应用

本文在利用GP模型进行径流预测的研究中，截取了广西天峨水文站某一年日平均径流量中的4月份前28 d数据构成训练样本，预测未来5 d该库区径流状况。在建立预测径流量的GP模型时，以连续p+1日径流量为一个训练样本。其中，前p日径流量构成训练样本的输入向量；第p+1日径流量为输出值；p为历史点个数，对结果有较大影响。例如：给定数据x1，x2，…，x6，…，建立GP模型过程中以X1=[x1，x2，，…，xp]，y1=xp+1作为训练样本(X，y)的第1个输入向量和输出值，其余训练样本输入向量、输出值依次类推。

经比较历史点数和协方差函数对回归、预测数据精度的影响，选择p=4个历史点数作为输入向量，SE作为协方差核函数；建立径流的GP预测模型，超参数的初始对数设置为：lgl=[lg(0.1)，lg(0.1)，lg(0.1)，lg(0.01)]；lg(sqrt(σf))=-1，以日径流量训练样本的极大似然为目标，经计算得到协方差函数最优超参数值为：lgl=[5.358，-0.844 3，0.947 0，-0.770 9，6.083 2]；lg(sqrt(σf))=-6.419 0。

利用上述训练好的GP模型对径流量样本进行训练和预测，并以平均相对误差绝对值MPE、均方误差MSE以及最大相对误差MRE作为衡量模型精度的评价指标，其值越小，预测模型描述样本数据则越精确。即

(10)

(11)

(12)

为了分析GP模型在径流量预测精度上较传统机器学习方法的优越性，本文同时利用传统BP模型和SVM模型对相同的训练样本以及预测样本进行预测，并与GP模型的预测结果相比较，结果见表1、2。从回归角度来说，基于传统BP、SVM模型的回归值都较GP模型相对误差大很多，反映了GP模型在数据回归上的相对优越性；从预测值相对误差来说，BP模型预测相对误差最小值和最大值分别为1.41%和6.18%，SVM模型分别为0.01%和5.24%，而GP模型仅为0.13%和2.71%。由此可看出，GP模型的预测精度明显优于传统BP模型和SVM模型；同时，从表2的预测结果MPE、MSE以及MRE来看，GP模型预测精度均优于传统BP模型以及SVM模型，反映了传统BP模型和SVM模型的预测误差偏高，不完全适用于此类小样本问题。

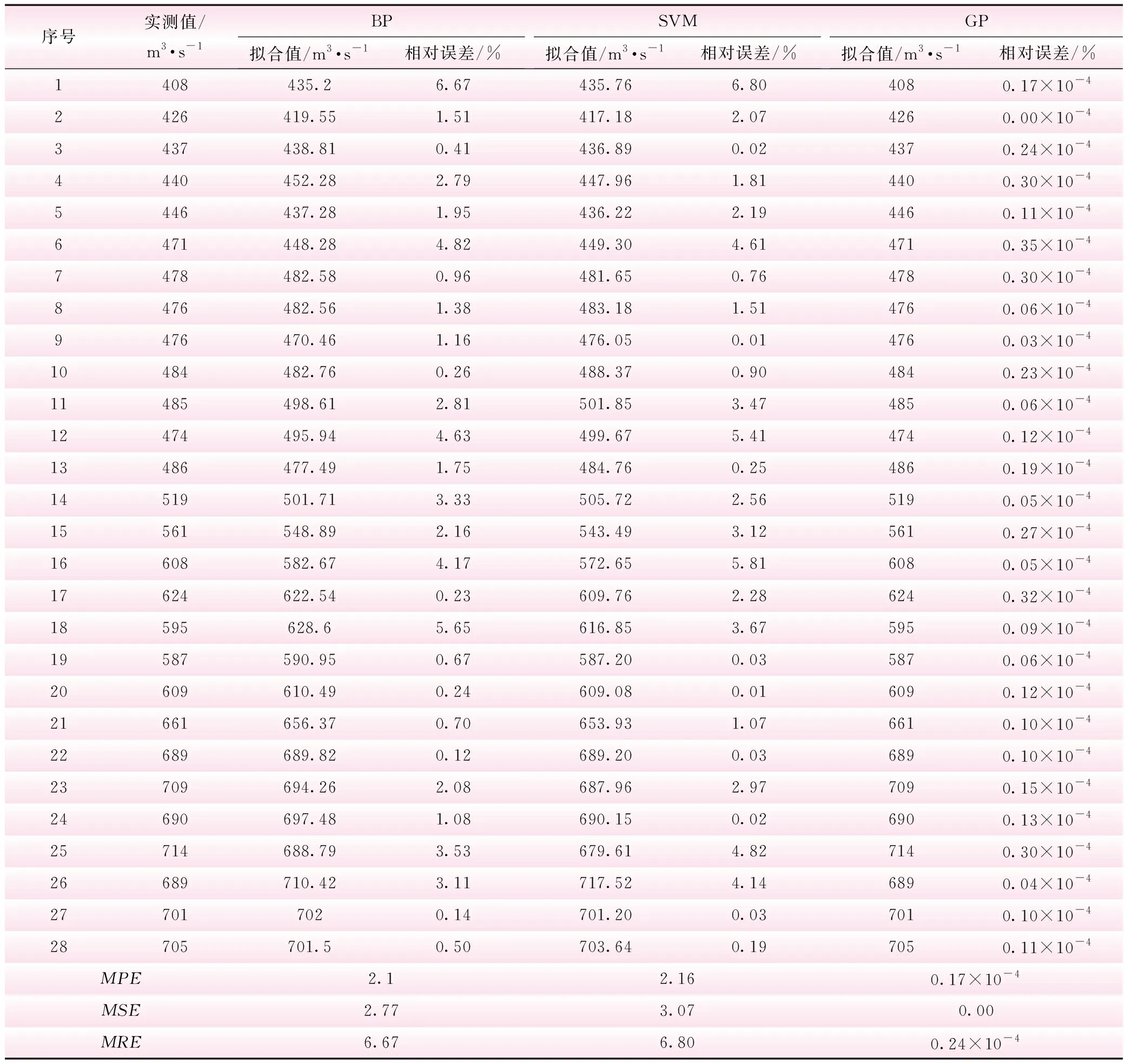
表1 基于BP、SVM、GP模型的训练值及训练误差

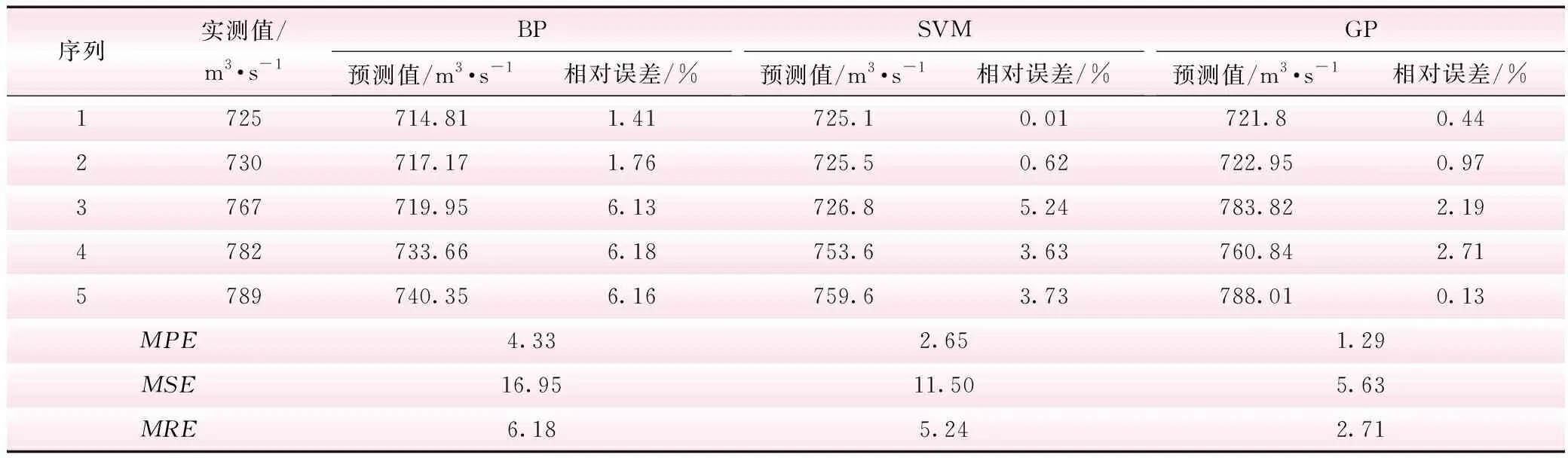
表2 基于BP、SVM、GP模型的预测值及预测误差

3 结 语

(1)本文以天峨站多年日径流量为基本资料，经GP模型、传统BP模型以及SVM模型径流预测结果分析比较可以看出：高斯过程回归模型模拟和预测能力要优于传统BP模型和SVM模型，模拟及预测效果平均相对误差小于5%。实例应用表明，GP模型应用于径流预测是可行的，是提高预测精度的有效方法。

(2)三种模型的预测结果都能满足工程实际需要；但相对来说，GP模型预测精度较前两者高，它成功克服了BP神经网络小样本推广能力欠缺问题，解决了SVM超参数难以确定的难题，体现出其独特的超参数自适应获取、输出具有概率意义等一系列的优越性以及良好的应用潜力，为更加精确的径流预测提供了一种新的思路，对于地区径流预测以及区域用水具有较大的指导意义。