融合L2 和KL保真项的图像恢复算法
2020-03-11刘洪琛刘朝霞
刘洪琛,刘朝霞,张 龙
中央民族大学 理学院,北京100081
1 引言
图像去噪是图像处理研究领域中经常研究的问题[1]。为了在去除噪声的同时更好地保持图像的清晰度、纹理特征等有用的信息,大量的去噪方法相继出现[2]。其中,1992 年Rudin 等提出的全变差正则化[3](Rudin Osher Fatemi,ROF)模型是迄今最为成功的图像复原模型之一。全变差正则化模型在图像去噪领域得到了广泛的研究与应用,但该模型有一个很大的缺点,易在相对平滑区域产生“阶梯效应”[4];基于L2范数的调和模型能有效地在平滑区域去除噪声,但处理图像的边缘易模糊[5]。2007 年,艾必刚等[6]利用分数阶微积分的定义,推导出分数阶微分梯度算子的频率滤波器。该滤波器对图像增强的效果较好,在增强细节的同时,能够有效去除噪声,但同时也增加了计算复杂程度;2016 年,石玉英等[7]提出了基于L1和L2混合保真项的图像恢复模型,充分发挥了L1和L2保真项的优点,有效地去除了高斯-椒盐混合噪声并保留图像的有效信息,但还是存在较大程度的阶梯效应;2018 年,马红强等[8]提出了基于改进栈式稀疏去噪自编码器的图像去噪模型,降噪效果良好。但是需要数据集训练模型,增加了训练成本;同年,尹芳等[9]提出了新的小波域Wener滤波器和Perona-Malik融合去噪算法,具有良好的去噪和抑制伪吉布斯的能力,但是对于计算时间的控制有待提升。
常见噪声有高斯噪声、脉冲噪声、泊松噪声等。高斯噪声是指它的概率密度函数服从高斯分布(即正态分布)的一类噪声,包括起伏噪声、热噪声等;泊松噪声是一种噪声分布符合泊松分布模型的与信号有关的噪声,包含在各种应用中,如射线照相、荧光显微镜、正电子发射断层扫描(Positron Emission Tomography,PET)、光学纳米检测和天文成像应用[5]。恢复被泊松噪声破坏的模糊图像是困难的。工业领域中,X射线图像检测作为一种无损、无接触和高分辨率的缺陷检测方法,X 射线在成像过程中,会受到不同类型噪声污染。X射线图像的噪声不能简单用单一的噪声模型来表示,它表现为高斯-泊松混合噪声,因此,去除高斯-泊松混合噪声具有很广泛的应用场景[10]。
为了有效抑制高斯-泊松混合噪声,获得更好的视觉效果,本文提出基于L2和Kullback-Leibler(KL)散度作为保真项(KL保真项)与两个正则项相结合的图像恢复的变分模型,并用增广拉格朗日算法进行数值实现。实验结果表明,针对目前的几种去除高斯-泊松混合噪声方法的局限性,所提出的新模型不仅保留了图像的边缘信息,减少了图像的“阶梯效应”,增强了图像的视觉效果,同时有效降低了均方根误差,得到了更高的峰值信噪比,CPU 的计算时间更短,并且不需要针对特定的训练集进行训练,提高了算法的效率,说明了算法的必要性和优越性。
2 图像去噪的变分方法
不失一般性,用M×N 矩阵表示一幅灰度图像,V=RM×N,离散的梯度算子∇:V →Q,其中Q=V×V ,f=Ku+n,f ∈V 是观察到的图像,u ∈V 是真实图像,n ∈V 为噪声算子,K:V →V 为模糊算子,M ,N 是图像大小。
2.1 调和模型
1977年,Tikhonov等[11]提出调和模型:
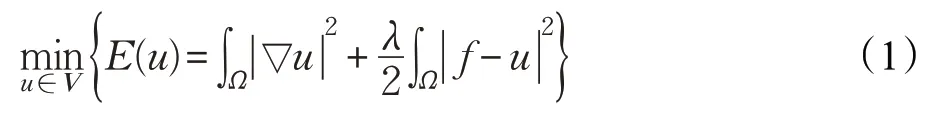
此模型能在在平滑区有效地去除噪声,但是该模型朝各个方向的扩散能力相同,容易模糊图像的边缘轮廓等细节信息。
2.2 ROF模型
基于L2保真项的全变差图像恢复模型(ROF 模型),是图像去噪中很成功的模型之一[3]。ROF模型为:
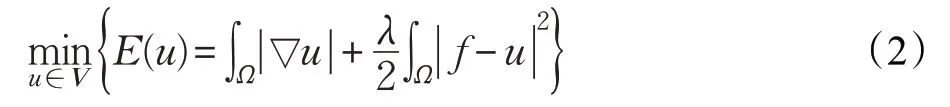
在模型中,保真项体现出所恢复的图像与原图之间的估计残差,估计残差越大,保真项的值越大,反之亦然。为保证函数为凸函数,保真项的指数取值范围是[1,2],取值2 时即为L2保真项。在各向同性扩散的过程中L2保真项针对不同的估计残差赋予其相应的权重[12-13],保证了在去除高斯噪声时的鲁棒性[14]。
此模型能很好保存图像的边缘特征,但是在处理图像相对光滑的区域部分会产生“阶梯效应”。
2.3 TV-KL模型
根据泊松噪声分布的特点,在文献[5,15]中使用Kullback-Leibler散度作为保真项(KL保真项)的全变差图像恢复模型(Total Variation Kullback-Leibler,TV-KL模型)用于解决这个问题。TV-KL模型为:
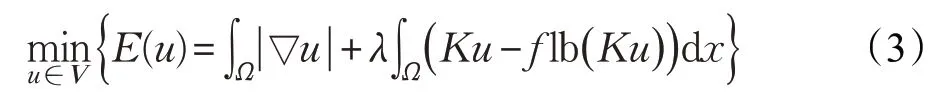
TV-KL 模型比标准的期望最大化(EM)重建(其中 不应用TV 正则项)[16]表现得更稳定和稳健,并且比ROF 模型去除Poisson噪声的效果更好,但也会产生“阶梯效应”。
2.4 改进的MS模型
由于‖ ‖∇uL1会产生阶梯效应,为了克服这个问题,文献[17]中提出了一个改进的模型——MS(Mumford-Shah)模型。文献[7]中提出了一个求解MS模型的近似模型:
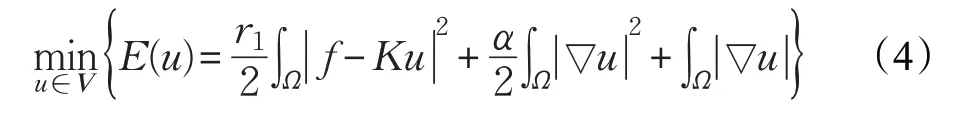
使用KL保真项的全变差图像恢复模型能有效地去除Poisson 噪声。基于模型式(4),相应去除Poisson 噪声的模型为:
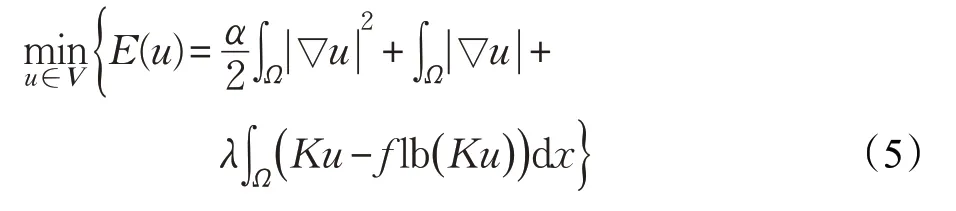
2.5 保真项混合模型
文献[10]中为了去除高斯-泊松混合噪声提出了基于混合Kullback-Leibler散度作为保真项和L2保真项的全变差模型,该模型为:
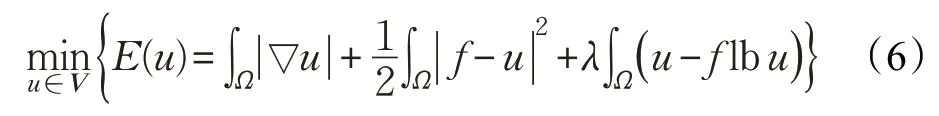
此模型中L2保真项能有效去除高斯噪声,基于混合KL保真项能有效去除泊松噪声,增强了去噪性能。
3 改进的图像恢复模型
综合考虑调和模型、TV-KL模型、改进MS模型、保真项混合模型的优点,并且受文献[6,18]的启发,提出了对高斯-泊松混合噪声去噪的图像恢复模型:
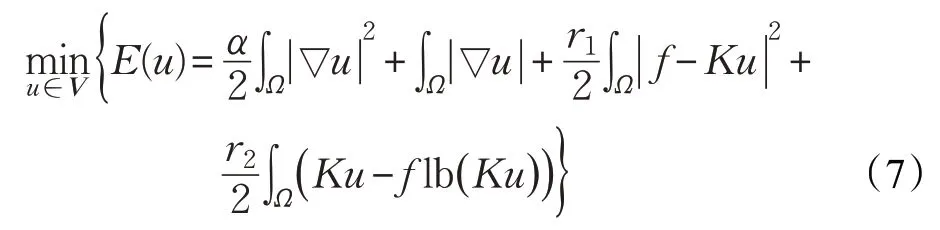
其中,α ≥0 是平衡正则项和保真项的参数,r1≥0,r2≥0用来调节高斯噪声和泊松噪声在总数据保真项中的比例,依据文献[10],比例系数可根据对噪声的先验知识或采用统计方法来确定。在此模型中,保真项。
从式(7)可知,当r1>0,r2>0,α=0,调整为模型(6),其可以较好地去除高斯-泊松混合噪声,并且保持边缘等细节信息[19];当r1=0,r2>0,α >0 时,调整为模型(5),可较好地去除高斯噪声,并且在一定程度上克服阶梯效应。
模型(7)和模型(5)不同的是,保真项采用L2和KL保真项的混合项,提高了去除高斯噪声的能力,一定程度上有效避免了阶梯效应;模型(7)和模型(6)不同的是,正则项采用的∫Ω||∇u2和∫Ω||∇u 的混合正则项,提高了在平滑区去除噪声的能力。因此,通过融合思想而提出的新模型充分体现了KL保真项和L2保真项的特点,集合了模型(5)(6)中的优点,可以更为有效地去除高斯-泊松混合噪声,并且优化了模型(5)(6)的不足,在一定程度上避免了阶梯效应,保持了边缘细节信息。在本文中,将提出的模型(7)记为新模型。
4 增广拉格朗日方法求解该模型
增广拉格朗日方法[10]的基本思想是引入拉格朗日乘子和惩罚项将带约束的问题转换成无约束问题进行求解。本章使用增广拉格朗日方法求解新模型。由于∇u 的不可微性和非线性,因此需要引入新的变量[20]。
下面引入两个新的变量p ∈Q 和z ∈V,上述式(7)等价于解下面这个带约束泛函的极值问题:

使用增广拉格朗日方法将上述带约束问题转换成下列不带约束的问题,定义增广拉格朗日泛函如下:
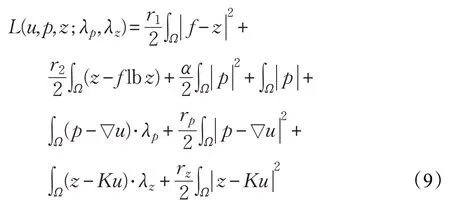
其中拉格朗日乘子λp∈Q,λz∈V ,正则化参数rp>0,rz>0。
求解问题式(3)转化为求解增广拉格朗日泛函的鞍点问题:
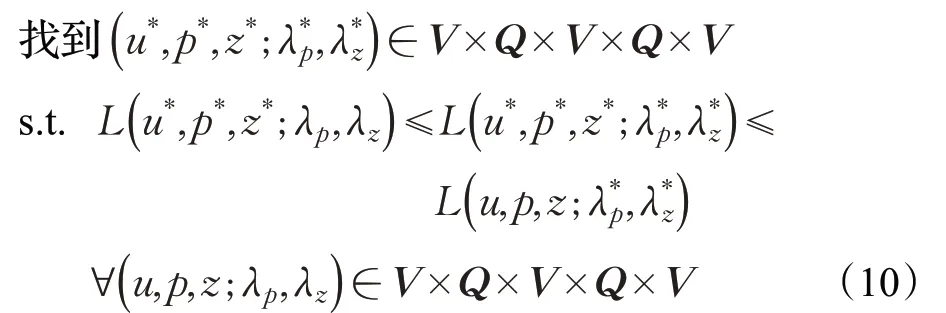
仿照文献[20],可以类似地证明鞍点问题(10)至少有一个解。对于上述鞍点问题,使用迭代算法解决,算法如下:
(1)初始化u0=0,p0=0,z0=0 和
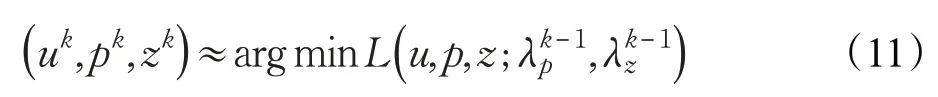
(3)更新拉格朗日乘子:

u-子问题。给定p,z,有:
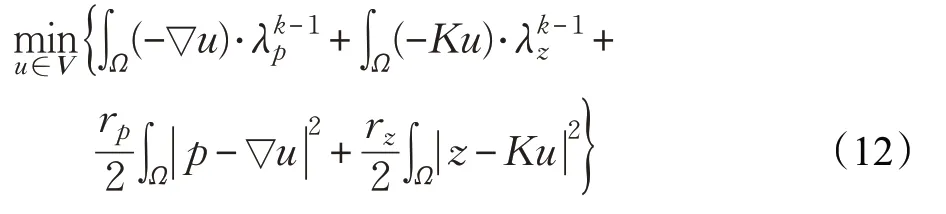
p-子问题。给定u,z,有:
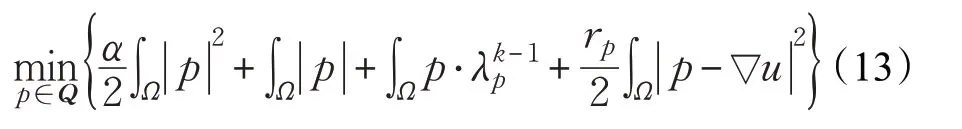
z-子问题。给定u,p,有:

下面使用交替求极小的算法求解上述三个子问题:
(1)解决u-子问题(12)
由边界条件和极小化条件[19-20],式(12)对应的Euler-Lagrange方程为:

使用快速傅里叶变换(Fast Fourier Transformation,FFT)求解上述线性方程,定义F(u) 为u 的傅里叶变换,通过傅里叶变换可计算u:

(2)解决p-子问题(13)式(13)简化为:

由边界条件和极小化条件[19-20],式(14)对应的Euler-Lagrange方程为:

参考文献[18]中对模型(15)算法收敛性的证明,以及结合文献[22]中对增广拉格朗日算法应用于TV模型的收敛准确性证明,可以证明提出的模型(7)在增广拉格朗日算法中是严格收敛的,准确性较高。
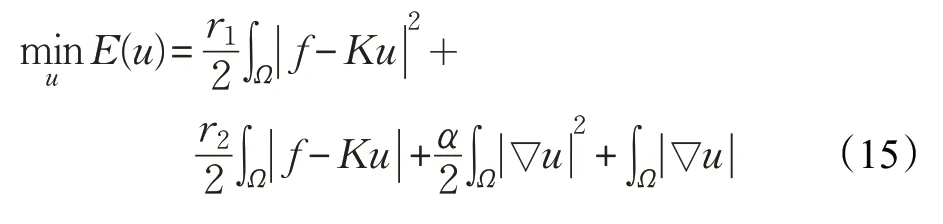

图1 测试图像
5 实验结果与分析
为了验证新模型的有效性,仿真实验均在AMD A8-3500M APU1.5 GHz CPU,24 GB RAM,Windows 7操作系统且运行环境为MATLAB 8.4.0.150421(R2014b)实验环境下实现。首先,给出模型参数的设置,参数拉格朗日乘子λp,λz是在算法迭代过程中引入的,它的选取对去噪结果图像的影响非常小,均取值为0,参考文献[10]、[23]与[24]中选取参数的方法,根据对噪声的先验知识,通过重复实验,选取r1=20 ,r2=10 ,α=2,rp=20,rz=4。在此实验中,对测试图像使用Matlab代码“imnoise(u,‘gaussian’,0,r)”添加方差为r 的高斯噪声(Gaussian Noise,GN),使用Matlab代码“imnoise(u,‘Poisson’)(根据图像数据数据生成泊松噪声,而不是向数据添加人为噪声)添加泊松噪声(Poisson Noise,PN),其中,u 是原始图像,为了简单起见,G(0.01)表示对测试图像添加方差为0.01的高斯噪声;P表示对测试图像添加泊松噪声:G(0.02)+P表示对测试图像添加方差为0.02的高斯噪声和泊松噪声。图1中的图像是从测试图像中选取的6 幅图像,Pepper 图像、Man 图像、Cameraman 图像、Tablet 图像、Lena 图像大小均为256×256,Brain 图像大小为709×591。为了客观评价图像去噪模型的性能,引入了峰值信噪比(Peak Signal to Noise Ratio,PNSR)和结构相似度(Structural Similarity Index,SSIM)两个客观评价指标。PSNR越大且SSIM越大,算法的去噪效果越好。其定义分别如下:

其中,f 是去噪后图像,u 是原始图像,M ,N 是图像大小,μf和μu分别是f 和u 的均值,σf和σu分别是f和u 的方差。实验中为了简介,所选取的对比模型有使用Kullback-Leibler 散度作为保真项的全变差图像恢复模型(TV-KL)、改进MS模型(Mix Regularization Term,MRT),以及保真项混合模型(Mix Fidelity Term,MFT)。
表1和表2给出了5幅测试图像在添加不同比例噪声时的峰值信噪比(PSNR)和结构相似度(SSIM)的比较,从表1 和表2 中可得,在添加方差较小的高斯-泊松混合噪声,新模型和MFT 模型的PSNR 与SSIM 比较接近,并且高于TV-KL模型和MRT模型。但是,随着添加方差增大的高斯-泊松混合噪声时,四种模型对应的PSNR都比较低,分析其原因,当混合噪声中高斯噪声方差较大时,图像中的边缘、纹理等几何结构信息丢失很多。在添加高斯噪声方差增大过程中,总体上新模型的PSNR 的值比其他模型大,SSIM 的值也大于其他模型,由于新模型结合了调和模型有效处理图像平滑区域与TV-KL 模型有效保存图像边缘信息的优势,并且L2保真项能有效去除高斯噪声,基于混合Kullback-Leibler散度作为保真项能有效去除泊松噪声。
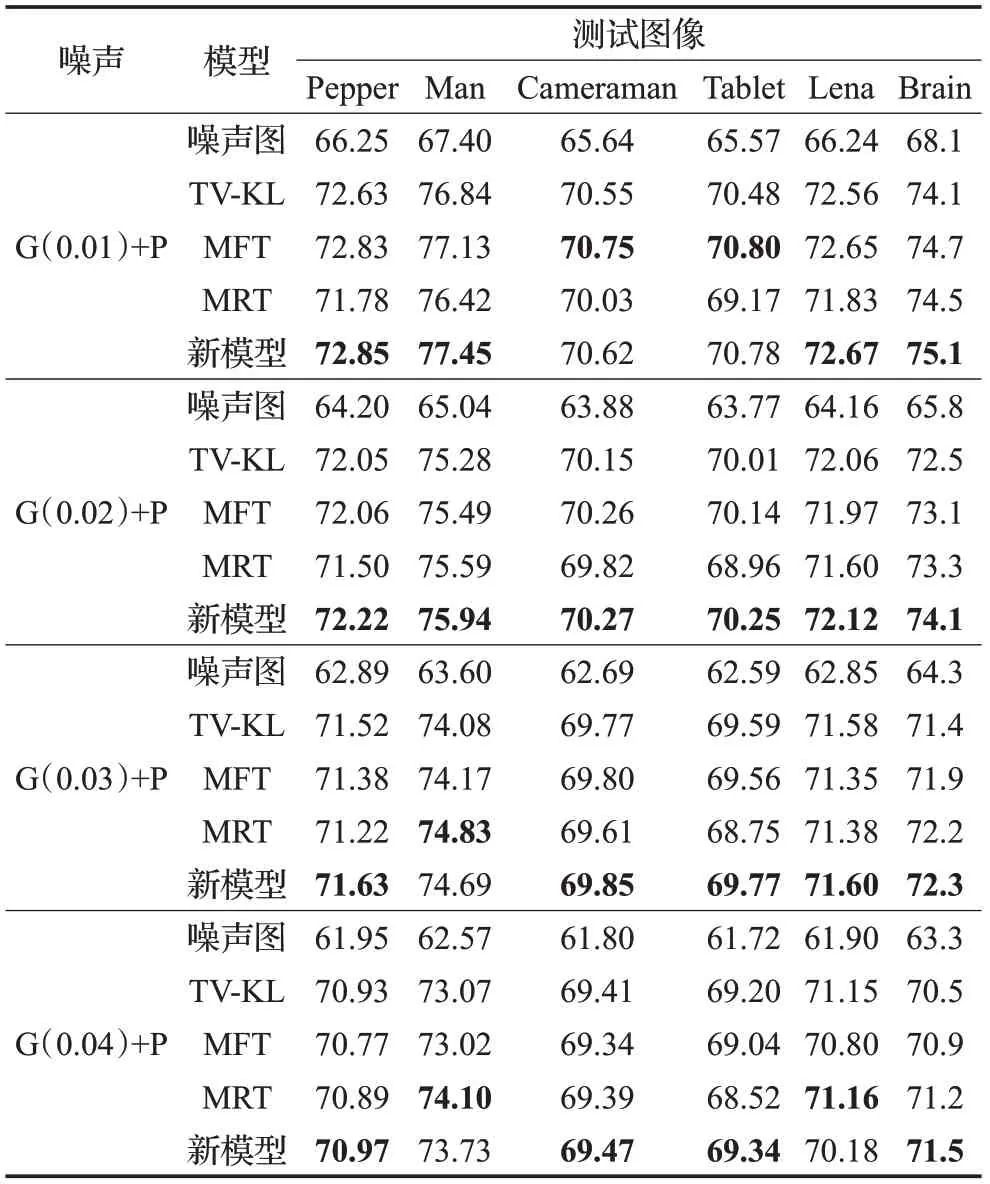
表1 去噪图像PSNR对比 dB

表2 去噪图像SSIM对比
图2 比较了在添加不同高斯-泊松混合噪声下Pepper 图像的恢复结果。第一行到第四行,对测试图像Pepper 分别添加G(0.01)+P、G(0.02)+P、G(0.03)+P、G(0.04)+P的混合噪声。Pepper图像的特点主要包含平滑和边缘部分,纹理较少。根据图像的视觉效果,针对添加不同方差的混合噪声,MFT 模型的图像恢复能力相对较弱,在添加混合噪声中高斯噪声方差较大时,去噪后得到的图像比较模糊,同时图像的结构和边缘信息也未能恢复。MRT模型对图像平滑部分的去噪效果较好,不足的是当图像添加高斯噪声方差增大时边缘细节信息丢失较多。TV-KL模型去噪能力很强,但是易产生“阶梯效应”。而提出的新模型不仅去噪能力很强,图像的结构和边缘信息得到有效的恢复,而且在一定程度上程度上抑制了“阶梯效应”。
对于如Man 图像、Cameraman 图像这类图像纹理、边缘等几何结构较多的图像,分别添加G(0.01)+P、G(0.02)+P、G(0.03)+P、G(0.04)+P 的混合噪声。选择其中一部分去噪后的图像,如图3和图4所示,其中图3的第一行添加G(0.01)+P 混合噪声,第二行添加了G(0.03)+P 混合噪声,整体而言,当添加混合噪声中高斯噪声方差较小时,新模型不仅去除了大部分噪声,轮廓更加简洁,纹理信息得到更好的保持,有很好的视觉效果,并且有较高的评价指标。虽然MRT 模型也有较高的评价指标,但是得到结果图像过于光滑,产生了“阶梯效应”。
对于如Lena图像、Tablet这类含有丰富纹理和边缘信息的图像,图5~7 中,四种方法得到的图像恢复结果和图2基本一致。从局部放大图像可看到,新模型去除高斯-泊松混合噪声的效果更好,噪声斑点较少(图5(i)),MFT 模型虽然能在一定程度上去除高斯-泊松混合噪声(图5(h)),但是当混合噪声中高斯噪声方差较大,MFT模型处理的结果图像变得模糊,图像分辨率降低,并且边缘特征信息也不能被保持(图6(h))。新模型可以有效地去除混合噪声并且较好地恢复了图像的纹理结构信息(图5(i)),较好地保留了图像的边缘信息,当混合噪声中高斯噪声方差较大时,新模型处理的效果也比较好(图6(i)和图7(i))。MRT 模型去除混合噪声效果也比较好(图5(g)),但是当混合噪声中高斯噪声方差较大时,MRT模型处理的结果图过于光滑(图6(g)和图7(g))。

图2 添加不同高斯-泊松混合噪声的Pepper图像恢复效果比较

图3 添加G(0.01)+P,G(0.03)+P噪声的Man图像恢复效果比较

图4 添加G(0.04)+P混合噪声的Cameraman图像恢复效果比较

图5 添加G(0.01)+P混合噪声的Lena图像恢复图像及局部放大图像比较

图6 添加G(0.03)+P混合噪声的Lena图像恢复图像及局部放大图像比较

图7 添加G(0.02)+P混合噪声的Tablet图像恢复图像及局部放大图像比较
最后,通过CPU 时间来比较几种模型的时间复杂度,表3统计了5幅图像在添加G(0.01)+P、G(0.02)+P、G(0.03)+P、G(0.04)+P 的混合噪声下的平均运行时间。由表3可知,新模型运行时间最短,其次是TV-KL,然后是MRT模型,MFT模型的运行时间最长。因此,从去噪的运行效率上来看,新模型相对于TV-KL 模型、MRT模型、MFT模型有比较强的优势。
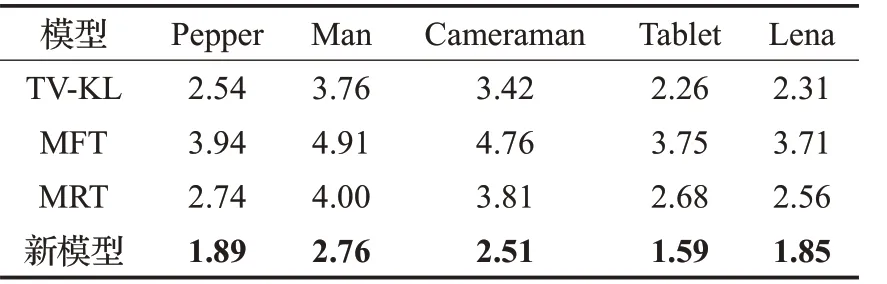
表3 不同混合噪声下图像恢复运行时间对比s
6 结束语
为了有效抑制高斯-泊松混合噪声,获得更好的视觉效果,本文在综合考虑TV-KL模型、MRT模型和MFT的优点,提出基于L2和KL保真项与两个正则项相结合的图像恢复的变分模型,并用增广拉格朗日方法对模型进行化简,化为三个子问题进行快速求解。为了加速计算,使用FFT 来解决u 子问题。对添加不同高斯-泊松混合噪声的测试图像进行数值模拟实验,实验表明提出的新模型有效去除了混合噪声,恢复了图像的纹理结构信息,图像的边缘特征被更好地保持,同时模型的算法也具有较高的执行效率,并且一定程度上抑制了“阶梯效应”。另一方面,本文提供的测试图片和实际生活需要处理的图片还存在一定的差距,因此,在后续的研究工作中,会寻找更加高效的、实现效果更好的去除高斯-泊松混合噪声的图像恢复模型。
