基于ParetoHeu和实例化失败统计的关联启发式方法

肖成龙，聂紫阳，王珊珊

辽宁工程技术大学 软件学院，辽宁 葫芦岛125105

1 引言

约束规划（Constraint Programming，CP）[1]是用于声明描述和有效解决约束满足及约束优化问题的软件技术，其在实际问题的建模方面具有高度灵活性和求解方式多样性，具有很高的学术价值和商业价值，在很多领域受到相关专家的高度关注。世界多所知名大学、科研机构和公司纷纷成立了约束规划研究中心，致力于约束规划的理论研究、工具研发及成果转化。目前，约束规划已经成功应用于包括航空[2]、电气[3]、运输[4]、密码学[5]、生物信息学[6]、生产调度[7]、机器学习[8]、图形图像[9]等诸多领域。

约束规划起源于20世纪60年代，并在20世纪80年代开始积极发展，其中约束逻辑规划CLP[10]的出现成为了约束规划领域研究的一座重要里程碑。20世纪90年代，约束规划进入实际使用时代，一些大学及商业公司相继研发了多种基于逻辑规划语言和面向过程语言的约束规划工具。1996 年，在美国计算机协会ACM 成立五十周年大会上，约束规划被列为21 世纪计算机领域战略研究方向之一。同年，约束规划期刊Constraints创刊。2005 年约束规划协会ACP 在法国成立，旨在促进约束规划的理论及应用发展，其每年举办的约束规划理论及实践国际会议CP 与整合约束规划、人工智能及运筹学国际会议CPAIOR（非约束规划协会举办）已成为约束规划研究交流的两项重要国际学术会议。此外，近些年，在IJCAI、AAAI、ECAI 等一些国际顶级的人工智能会议上，都有对约束规划相关研究的专题讨论。当前，约束规划已成为人工智能领域的一个研究热点。

约束规划采用约束传播[11]和回溯搜索[12]来解决问题，约束传播用于修剪搜索空间，回溯搜索对搜索空间进行遍历，实现问题求解。在搜索过程中如何选择变量构建搜索树是一个十分关键的步骤，选择“正确”变量赋值可减少无效搜索分支，提高求解效率。

假设一个简单的约束满足问题包含n 个白变量和m 个黑变量。白变量值域为{0，1}，黑变量值域为{0，1，2，…，m-2}，对于黑变量要求其两两取值不同，而白变量没有约束限制。可以很容易分析出该约束满足问题没有满足约束条件的解。假设在回溯搜索过程中采用的变量排序启发式优先选择白变量进行赋值，待所有白变量赋值完成后再选择黑变量赋值，则该启发式对应的搜索树如图1左所示，求解时会对整个搜索空间进行遍历。若在开始搜索之后采用动态的变量排序启发式选择可能导致搜索失败的变量构建搜索树，则搜索树如图1右所示，可以看到合适的变量排序启发式策略可对搜索树进行有效剪枝，提高问题求解效率。

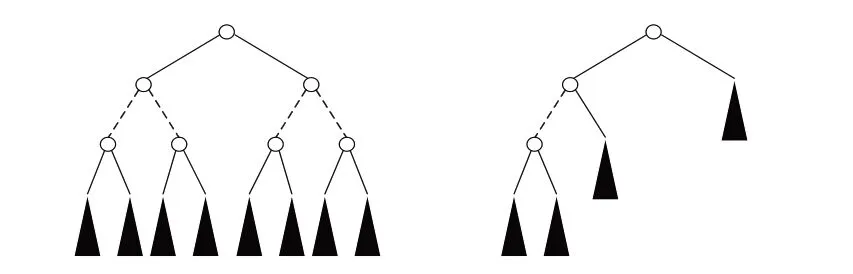
图1 应用变量排序启发式效果示例

目前，针对变量选择已有多种独立和组合变量排序启发式被提出，包括dom[13]、deg[14]、IBS[15]、ABS[16]、CBS[17]、CRBS[18]、dom/deg[19]、dom/ddeg[20]、dom/wdeg[13]等。这些启发式基于变量属性或问题求解状态选择合适变量，加快搜索进程。但由于待解决问题种类、特征不同及启发式自身特性等原因，一个变量排序启发式即使在多数问题求解上剪枝效果较好，也无法保证在所有问题求解上都要优于其他启发式。从搜索过程出发寻找利用问题求解通性，屏蔽问题之间的差异对求解过程的影响，提出和研究改进更为有效、适用范围更广的独立或组合的通用启发式仍是约束规划研究中一个重要的研究方向。

本文采用一种新颖的变量排序启发式组合策略ParetoHeu[21]将经典的启发式dom/wdeg与基于关联的启发式CRBS（Correlation-Based Search）结合，以提高和增强CRBS对问题的求解效率和通用性。同时，加入基于实例化失败次数的权值统计方法[22]进一步对待实例化变量进行选择，提出了crbs-sum及crbs-max的两种改进变量排序启发式PICS 和PICM。实验在Choco[23]约束求解器上实现，并在多个约束满足问题实例上进行测试。实验结果表明PICS 和PICM 与crbs-sum、crbsmax 及其他经典主流启发式相比，在多个问题实例求解上，两种新变量排序启发式方法的求解效率高于其他启发式。

2 相关工作

变量排序启发式对回溯搜索效率有着重要影响，选择合适变量实例化可以显著减小搜索空间，从而更快地解决问题。在一些规模较大的问题求解上，一个“正确”或“错误”的决定可以使求解时间产生指数级的变化。目前，已有多种变量排序启发式相继提出。这些启发式大多遵循“失败优先”原则，即优先选择可能导致搜索失败的变量进行实例化，并基于变量值域大小、约束图、约束触发失败次数等特征定义得分函数，在每个搜索节点上选择得分函数最高的变量实例化。

变量排序启发式可分静态变量排序启发式和动态变量排序启发式两类。静态变量排序启发式在搜索之前计算变量得分并确定实例化变量序列，在搜索过程中不会对变量序列进行调整，一些已经提出的静态排序启发式包括选择相关约束最多变量的启发式deg[14]、选择最小约束网络宽度的启发式width[12]等。动态变量排序启发式在搜索期间动态更新变量得分并调整变量排序。在实际使用中，动态排序启发式的应用多于静态排序启发式。早期的独立或组合动态排序启发式都是根据变量基本属性来选择变量，如第一个动态排序启发式dom[13]基于值域大小选择变量、动态的deg 启发式ddeg[14]、dom/deg[19]、dom/ddeg[20]等。之后，一些基于问题求解状态和自定义变量特征的启发式相继提出，包括基于影响的启发式IBS（Impact-Based Search）[15]、基于冲突的启发式wdeg[24]、基于活跃度的启发式ABS（Activity-Based Search）[16]、dom/wdeg[13]、基于约束紧度和解密度的启发式RHO[25]等。目前，IBS、ABS 和dom/wdeg 是大多数约束规划求解器中主要使用的三种启发式。IBS启发式通过衡量变量实例化导致潜在搜索空间的减少程度选择变量。Wdeg启发式为每个约束赋予一个权重值，当搜索产生冲突时，相应约束的权重会增加，启发式会优先选择约束权重之和最大的变量。ABS 启发式基于每个变量值域变动频率选择变量。近些年提出的一些较为新颖的启发式及改进启发式主要有基于统计变量赋值在解中出现的频率的CBS（Count-Based Search）[17]、基于失败原因解释的改进wdeg[26]、优先选择最后冲突的变量的LC（Last Conflict heuristic）[27]、冲突排序的COS（Conflict Ordering Search）[28]、基于约束紧度的改进dom/ddeg和dom/wdeg[29]、基于变量关联的CRBS以及基于帕累托最优的启发式组合策略ParetoHeu等。这些变量排序启发式都基于问题变量、约束的自身属性或研究人员自定义属性来选择变量，不考虑问题本身的性质，从而将问题本身与变量选择分离，使其可用于对大部分问题求解，而不是只针对一个或一类问题，具有一定的通用性。因此，对于提高变量排序启发式通用性研究的着手点也在于如何利用变量、约束的基本属性或与其相关的自定义属性来选择变量。此外，在Li等人的研究[21]中，实验结果显示组合启发式在多数情况下要优于原单启发式，早期的dom/ddeg、dom/wdeg等组合启发式也很好地印证了这一点，文章中应用其提出的ParetoHeu 启发式组合策略在问题求解上平均CPU时间要少于传统的顺序启发式组合策略和得分乘积启发式组合策略，ParetoHeu为组合启发式提供了一个新的思路。

除上述独立启发式与组合启发式研究外，还有一些关于自适应变量排序启发式的研究，这类启发式称为超启发式（hyper-heuristic）[30]，其根据解决方案数量、目标函数值、已运行时间等问题状态特征，从包含多个独立启发式的序列中为搜索过程动态选择启发式。一些研究[21]包括基于机器学习[31-32]和基于演化计算[33]的超启发式。目前，这些方法尚未在主流约束规划求解器中实现和应用。

3 相关定义

约束满足问题（Constraint Satisfaction Problem，CSP）[34]源于人工智能研究，多为NP-hard 问题，可定义为三元组P=＜X,D,C ＞，其中X={x1,x2,…,xn}为变量集，D={dom(x1),dom(x2),…,dom(xn)}为X 中各变量值域dom( xi)的集合，每个变量值域大小记作|dom( xi)|。为约束集，约束是各变量取值的制约关系。变量xi涉及约束的个数称为度（degree），每个约束ci可记成( scp( ci),rel( ci))，scp( ci)={ x1,x2,…,xr} 是一个有序的变量子集，为约束ci所涉及到的变量，rel(ci)是scp(ci)内每个变量值域笛卡尔乘积D(x1)×D(x2)×…×D(xr)的一个子集，每个元组τ ∈rel(ci)是一个有序的变量取值的集合，可定义为＜(x1,a1),(x2,a2),…,(xr,ar)＞，其中aj∈dom(xj),j=1,2,…,r。

约束满足问题的求解是依次为每个变量在其值域中选择一个合适的值，使所有变量赋值后满足全部约束，为变量赋值的过程称为实例化（instantiate）。在约束规划中常采用约束传播与回溯搜索结合的方式对CSP进行求解。约束传播使用相容性技术（consistency technology）在搜索前和搜索过程中从变量值域里移除不属于任何可行解的值，进而减小搜索空间，加快搜索进程，出于时间复杂度和空间复杂度的考虑，约束求解器中最常使用的为弧相容（Arc Consistency，AC）[11]和边界相容（Bounds Consistency，BC）[11]算法。回溯搜索用于实现对问题求解，在搜索过程中会使用变量排序启发式选择待实例化变量构建搜索树，变量排序启发式会对搜索效率产生巨大影响。在回溯搜索期间，已实例化变量称为PastVar。相反，未实例化变量称为FutVar。

4 基于ParetoHeu和实例化失败统计的关联启发式方法PICRBS

4.1 PICRBS思想

为进一步提升和增强关联启发式CRBS 对问题的求解效率和通用性，本文提出了基于ParetoHeu 和实例化失败统计的关联启发式PICRBS，并根据CRBS 中两种变量选择方式crbs-sum 和crbs-max 提出了具体方法PICS 和PICM，PICS 与PICM 的区别在于两种方法计算CRBS启发式得分方式不同。

PICRBS 采用基于帕累托最优（Pareto optimality）的启发式组合策略ParetoHeu 将启发式CRBS 与dom/wdeg 结合，在未实例化变量中选择最可能导致搜索发生冲突的变量，加入帕累托候选变量集合中。之后使用基于实例化失败次数的权值统计方法对帕累托候选变量集合中的变量做进一步筛选。已有研究发现变量实例化的失败次数在一定程度上可说明该变量与已实例化变量集之间的冲突关系[22]，因此选择实例化失败次数最多的变量作为待实例化变量可增加搜索过程中发生冲突的可能，从而使搜索树尽早剪枝，加快问题求解。

PICRBS通过对变量值域在搜索中改变频率以及变量相关约束导致回溯次数的双重衡量，从变量自身及约束两个方面考虑选择该变量导致搜索发生回溯的可能，使变量实例化后搜索树可最大化剪枝。同时，双重衡量也可防止因单启发式对问题求解的不适用而导致问题求解时间过长甚至无法求解，增强了启发式的通用性。在组合启发式后使用基于实例化失败的权值统计方法，选择实例化后导致搜索冲突可能性相对更高的变量，可对启发式求解问题的效率做进一步提升。

4.2 PICRBS流程

PICRBS流程图如图2所示。在搜索期间，PICRBS维持存储所有变量对关联性的对称关联矩阵、统计约束权值和各变量实例化失败次数。进行变量选择时，PICRBS遍历未实例化变量集合FutVars，对集合中变量xi计算启发式CRBS（crbs-sum/crbs-max）和dom/wdeg得分（两种得分分别记作sc1 和sc2），并依次与帕累托候选变量集合ParetoFront 中的变量xj比较两种启发式得分，若sc1[xi]≥sc1[xj]且sc2[xi]＞sc2[xj]或sc2[xi]≥sc2[xj]且sc1[xi]＞sc1[xj]，称变量xi支配（dominate）变量xj，PICRBS 将xi作为帕累托候选变量添加到候选变量集合ParetoFront中，同时由xi支配的变量xj都将从集合中移除。如果xi和xj的启发式得分相同，xi被添加到ParetoFront中。对于ParetoFront中得分相同的变量，PICRBS 通过变量实例化失败次数进行进一步筛选，选择搜索期间实例化失败次数最多的变量作为待实例化变量加入集合MaxInsta中，若MaxInsta中存在多个失败次数相同的变量，则对这些变量进行随机选择。在变量实例化后，如果搜索未发生冲突，对关联矩阵进行更新。反之，更新关联矩阵同时对约束权值和变量实例化失败次数进行加权更新。

关联矩阵更新方式及PICRBS中CRBS启发式得分计算规则如下：当选择某个变量xi实例化并进行约束传播后，若发生冲突，即有变量值域被清空，关联矩阵按式（1）规则进行更新，其中X'=X{xi}为X 去除xi后的变量集合，为更新前的关联值。

若无冲突发生，则按式（2）规则更新关联矩阵，dom'(xj)为约束传播后变量xj的值域，U 和N 分别为约束传播后值域发生变化和没有变化的变量集合。

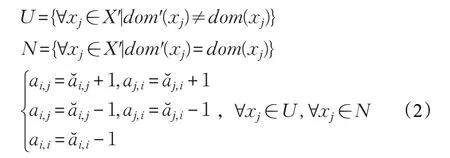
图2 PICRBS流程图

启发式CRBS 计算得分有两种方式，crbs-sum 与crbs-max。PICS和PICM 分别采用这两种计算方式，计算规则如式（3）和（4）所示。 Pc(xi)为已实例化变量与xi关联值的和，Fc(xi)为未实例化变量与xi关联值的和，在计算时变量xi记为未实例化变量，参数0 ≤θ ≤1用于调整Pc(xi) 与Fc(xi) 的组合关系。在计算crbssum(xi) 或crbs-max(xi) 后，crbs-sum 和crbs-max 会将crbs-sum(xi)/dom(xi) 和crbs-max(xi)/dom(xi) 作 为 最终启发式得分。

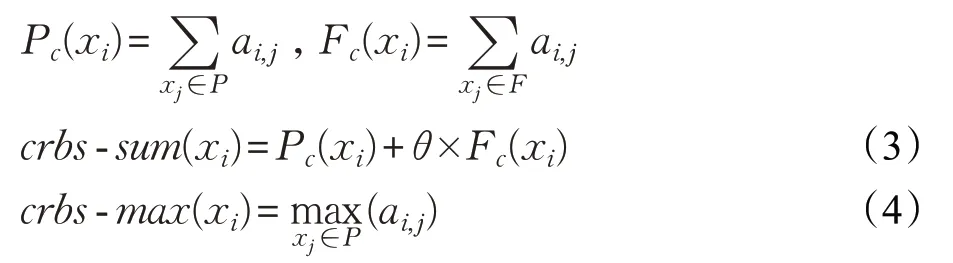
约束权值weight[c]是启发式dom/wdeg为每个约束c ∈C 设置的属性值，初始为1，当变量实例化导致冲突时，权重值加1。作为变量得分。式（5）为变量权重和计算公式，其中FutScp(c)为scp(c)中的未实例化变量集合。

变量实例化失败次数权值统计公式如式（6）所示，其中var_ fails 为变量实例化失败次数，dom 为变量值域大小。

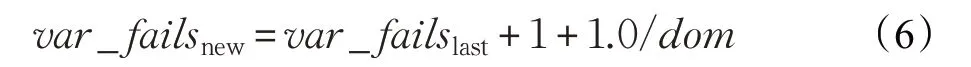
PICRBS关键部分伪代码如下：

算法1 PICRBS(FutVars,sc1,sc2,insta)

输入：FutVars,sc1,sc2,insta

输出：MaxInsta

1.ParetoFront←Ø；

2.MaxInsta←Ø；

3.tempMaxInsta=−1；

4.for each variable xiin FutVars do

5. isPareto←true；

6. for each variable xjin ParetoFront do

7. if xidominates xjthen

8. ParetoFront ←ParetoFront{xj}；

9. else

10. if xjdominates xithen

11. is Pareto←false；

12. end if

13. break；

14. end if

15. end for

16. if isPareto then

17. ParetoFront←ParetoFront∪{xi}；

18. end if

19.end for

20.for each variable xiin ParetoFront do

21. if insta[xi]>tempMaxInsta then

22. tempMaxInsta=insta[xi]；

23. MaxInsta←Ø；

24. MaxInsta←MaxInsta∪{xi}；

25. else

26. if insta[xi]==tempMaxInsta then

27. MaxInsta←MaxInsta∪{xi}

28. end if

29. end if

30.end for

31.return MaxInsta

伪代码中参数FutVars、sc1、sc2、insta 分别为未实例化变量集合、CRBS 启发式得分、dom/wdeg 启发式得分和待解决约束满足问题中所有变量集合。方法开始时先建立两个空集合ParetoFront 和MaxInsta 分别用于存储帕累托候选变量以及实例化失败次数最多变量，tempMaxInsta 记录当前最大实例化失败次数。在构建搜索树时，对于未实例化变量集合FutVars 中的变量进行遍历，选择两种启发式得分都最高的变量加入集合，在遍历过程中对ParetoFront 进行动态更新。待所有变量遍历完毕后，通过基于变量实例化失败次数对ParetoFront 中变量做进一步筛选，选择以往搜索中实例化失败次数最多的一个变量或多个变量加入MaxInsta 集合，若MaxInsta 中多于一个变量，则对变量进行随机选取，最后返回一个变量构建搜索树。

5 实验及结果分析

5.1 实验数据

本文实验数据为国际测试通用的约束满足问题，其中一部分为2018年约束求解器竞赛基准问题。实验中，对于每类问题分别选取了不同规模的实例，共177 个，这些实例均可在http：//xcsp.org/上下载。测试所用的基准约束满足问题包括：SportsScheduling、StripPacking、SocialGolfers、MagicHexagon、GracefulGraph、Frb、Bibd、QueensKnights、Hanoi、Driverlogw、Eternity、ColouredQueens、Crossword。

5.2 实验配置及说明

实验在约束求解器Choco 4.0.8上完成。实验环境及配置为JDK8，Windows操作系统，英特尔i5-3337U双核处理器1.8 GHz，4 GB DDR3内存。

实验中与PICS 和PICM 对比的启发式方法包括：IBS[15]、ABS[16]、dom/wdeg（d/w）[13]、crbs-sum（c-s）[18]和crbsmax（c-m）[18]。在实验中，采用geometric重启策略，初始cutoff=10，ρ=0.1。cutoff 为最大失败数，ρ 控制重启之后最大失败数增长，公式为cutoff=cutoff'+init_cutoff×ρk。 cutoff′ 为上一次失败次数，k 为重启次数。搜索使用二元分支深度优先搜索，求解时限为1 200 s。对 于 启 发 式crbs-sum 和PICS，参 数θ 设 为0.1。在PICS 和PICM 中为了选取最高得分，dom/wdeg计算采用对于实验中的随机数，随机种子均设为0。

实验测评指标包括启发式成功求解问题实例数量，所有启发式均可求解问题的平均时间、平均搜索树节点。在对时间指标统计时，为避免极端求解时间对实验评估产生影响以及更准确地反映问题求解时间，实验对每个问题实例进行5次求解，最终统计时除去最长与最短求解时间，取剩余3次求解时间的平均值。

5.3 实验结果及分析

表1 给出了各启发式对于测试问题实例的成功求解个数、平均时间和平均节点。问题名称后括号内为实验选取问题实例个数，时间和节点后括号内为该类问题启发式均可求解实例个数。PICS 和PICM 作为本文提出的c-s 和c-m 改进启发式分别在11/13、9/13 个问题求解上相对于后两者搜索树节点有所减少，在Graceful-Graph 问题上最为明显，分别减少了99.75%和98.73%，求解时间有大幅度提升。除GracefulGraph 问题外，在其他搜索树节点减少的问题中，两种改进启发式在搜索树节点上相对于改进前平均减少46.1%和50.47%，求解时间平均降低了44.83%和29.65%。PICS和PICM分别在10、8、9和10、6、7个问题求解上优于三种主流启发式IBS、d/w、ABS。

各启发式总求解实例数量及总平均时间和节点数如图3所示。从图中可以看到，IBS、d/w、ABS、c-s、c-m、PICS和PICM在限制时间内依次成功求解了85、90、85、82、87、96、90 个问题实例，PICS 求解数量最多，c-s 最少。同时，PICS在全部求解实例中平均表现最优，在多个共同求解问题中无耗时较长的求解结果，平均时间比次优的PICM 少近9 s，平均搜索树节点减少了三分之二。IBS 启发式在多数问题求解中时长和节点数均大于其他启发式。两种主流通用启发式ABS、d/w在个别问题求解上表现并不理想。从最终结果来看，在测试问题实例上，c-s与c-m启发式仅优于IBS启发式。他启发式，PICM 启发式在问题实例driverlogw-09 求解上与c-m相比搜索树节点少于后者，但求解时间恰恰相

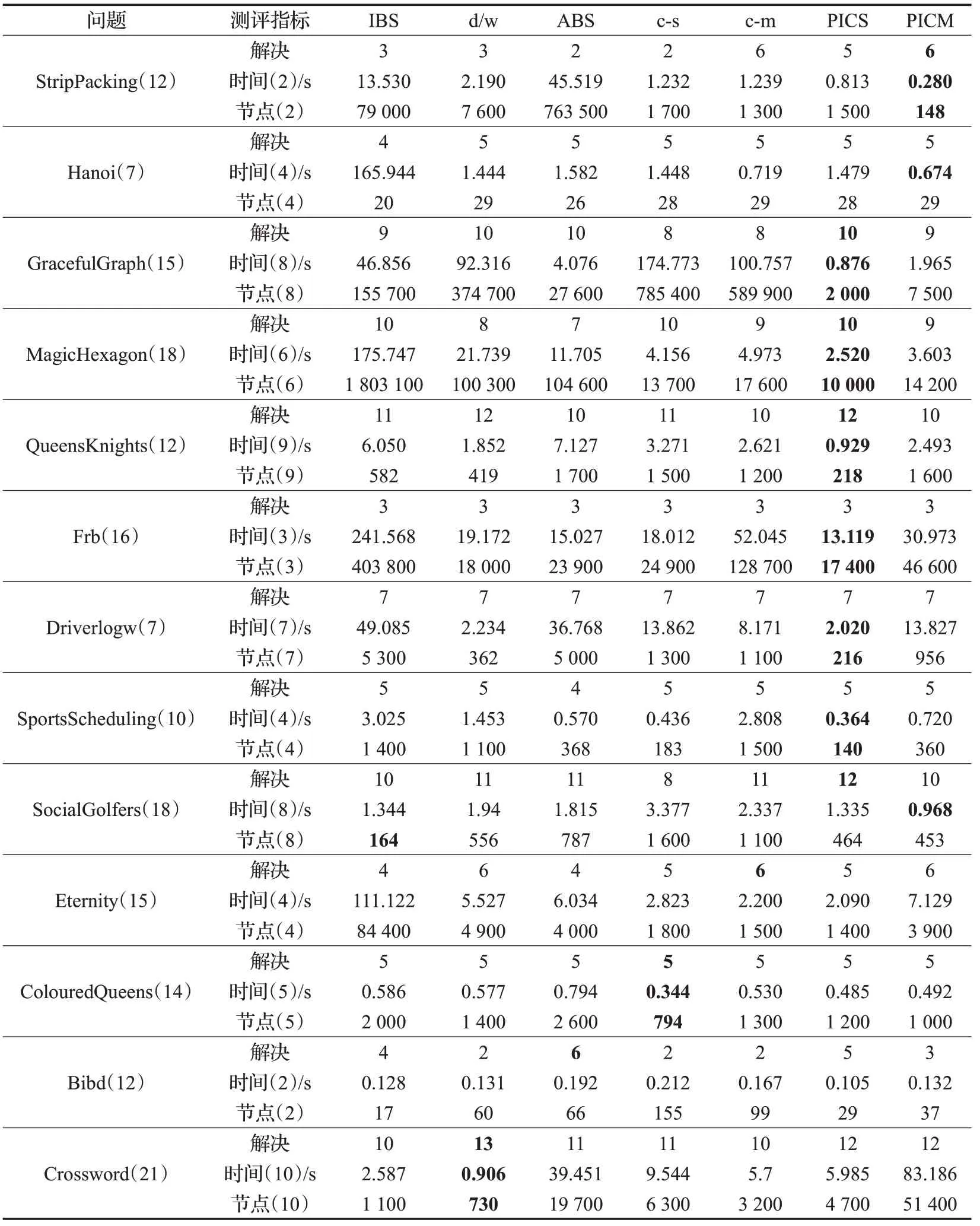
表1 各启发式对测试问题求解个数、平均时间和平均节点

图3 各启发式测评指标比较

一般来说，搜索树节点数与运行时间成正比，节点数越大求解时间越长，但由于问题特性和启发式时间复杂度较高等原因，一些启发式在求解某些规模较小的问题实例时，会出现搜索树节点数少于其他启发式而求解时间较长的情况。表2 给出了各启发式对部分问题实例的求解时间和节点的实验结果（TO 表示求解超时）。如表2 所示，IBS 启发式在求解问题实例Hanoi-06 中搜索树节点为其他启发式的一半，但其求解时间远大于其反。实验中，这种情况在IBS 启发式上体现较为明显，但求解时间不会与Hanoi-06 实例一样与其他启发式相距悬殊。

表3 加入权值统计方法前后启发式节点对比

表3给出了CRBS与d/w采用ParetoHeu结合的启发式在加入基于权值统计方法前后部分问题实例求解的搜索树节点数量。在多个问题实例中，加入基于权值的统计方法可以进一步减少搜索树节点，加快问题求解。需要注意的是，在一些问题实例上加入该方法也会导致节点数增多，如表3中后两行所示。从所有问题求解的最终结果来看，加入权值统计方法的组合启发式效果较好。

总体而言，在多种问题实例进行测试结果显示，采用ParetoHeu结合d/w并加入基于实例化次数权值方法的关联启发式方法，相对于原始启发式有了很大性能提升，并在一些问题上与主流启发式相比具有竞争力。

6 结束语

本文采用基于帕累托最优的启发式组合策略ParetoHeu将启发式CRBS与经典启发式d/w相结合，以提高CRBS的求解速度和增强通用性，同时加入基于实例化失败次数的权值统计方法，以进一步减小搜索树大小，提高求解效率，提出了两种CRBS 改进启发式PICS与PICM。在多个国际通用测试约束满足问题求解上，PICS 和PICM 相对与改进前平均搜索树节点和求解时间有所减少，并与主流启发式相比具有一定竞争力。未来将对多种变量排序启发式及约束规划求解问题的特征做进一步研究，以提出更为有效的独立或组合通用启发式。