政府补贴对企业生产率的双刃剑效应——基于异质性企业理论和门槛回归方法的研究

李 峰，王亚星

（中国人民大学商学院，北京 100872）

改革开放40年以来，我国经济活力得以充分释放、经济潜力得以充分挖掘，创造了经济快速增长的奇迹。但2012年以来经济增长减速，暴露了我国当下劳动力供给不足、人力资本改善增速放慢、投资回报率下降、资源重新配置空间缩小以至全要素生产率增长减速等诸多供给侧问题［1］。因此，原先依靠要素投入、要素重新配置的简单粗放型增长路径将不可持续，政府和企业必须将经济增长重点从原先的要素扩张转移到全要素生产率提升上来。事实上，我国政府历来鼓励企业自主创新，积极为企业营造创业创新的有利外部环境，同时也为企业提供补贴，引导企业技术研发、发展战略性新兴产业。根据中国工业企业数据库的统计，政府对企业的补贴总额从1998年的近150亿元增至2013年的近1 448亿元。那么，政府的大量补贴是否真正实现了预期效果，受补贴企业的生产率是否因此得以提升？这正是本文试图回答的问题。

政府补贴的合理使用以及企业生产率的提升都与我国社会总体福利密切相关。但是，目前对于政府补贴与我国企业研发创新、生产率提升的关系，既有研究莫衷一是，对机理的研究尚存在未解决的黑箱［2-3］，政府补贴对于企业研发创新、生产率提升，无论是具有促进作用［4-5］，还是消极的抑制作用［6-7］，都有相应的理论和实证支撑。政府补贴效果如何，关键在于企业基于自身利润最大化目标如何选择政府补贴的利用方式，是直接作为收益留存还是投入研发创新？而在企业异质性背景下，这又取决于企业既有的异质性生产率。缺乏对这一作用机制的深入分析，则可能掩盖了政府补贴对企业生产率的真实影响，从而导致不稳健的研究结果。因此，政府补贴对企业生产率的作用机制和差异化影响亟须更为严谨、丰富的理论探讨、模型刻画以及实证检验。本文运用并拓展异质性企业理论［8］，弥补了相关既有研究缺乏系统性的模型分析框架以及忽视企业既有生产率异质性和相应自选择（self-select）的不足，刻画了政府补贴对企业生产率的双刃剑效应，并且借助与理论模型高度契合的门槛回归方法［9］，力图实现理论模型与计量模型的相互补充、理论推论与实证结果的相互印证。

本文借鉴MELITZ［8］的异质性企业模型以及BUSTOS［10］的企业研发创新自选择模型，着重刻画了企业基于既有的异质性生产率，对政府补贴和研发创新②既有研究［11-12］发现，政府补贴对企业生产率的提升通过促进技术改进而非规模经济性实现，这表明企业自选择的研究重点应当落在企业借由政府补贴实现的研发创新活动上。做出差异化的自选择，从而导致政府补贴对企业生产率的双刃剑效应。既有生产率处于研发创新门槛生产率（innovation cutoff productivity）以上的企业因其更高的生产率而具有更大的生产和销售规模，自身生产率的边际提升能够带来更大规模的成本下降和利润增加，由此，企业更倾向于将政府的补贴资金投入研发创新活动，以更高的生产率获取更大的利润；既有生产率处于研发创新门槛生产率以下的企业，囿于自身有限的规模，生产率的边际提升带来的利润增长不足以弥补其为提升生产率而投入的研发创新成本，于是将政府补贴直接作为企业盈余而不投入研发创新才是利润最大化的自选择；而既有生产率处于幸存门槛生产率（survivalcutoffproductivity）以下的企业基于自身利润最大化目标，非但不会利用政府补贴进行研发创新，反而将其直接作为收益留存、弥补原先的亏损，使得日常经营得以维系，这实际上挽救了原先在正常的市场竞争机制下本应被淘汰的落后企业，这也是“僵尸企业”的重要来源之一。因此，对于既有生产率处于研发创新门槛生产率以上的企业，政府补贴激发了企业研发创新并促进了企业生产率提升；对于既有生产率处于幸存门槛生产率以下的企业，政府补贴只会挽救生产率更低的落后企业，从而使得政府补贴与企业生产率之间呈现显著的负向关系，在数据上表现为政府补贴“阻碍”了企业生产率的提升；而对于既有生产率处于两者之间的企业，政府补贴并不影响企业的研发创新，对企业生产率亦不会产生显著影响。最后，本文分别利用LP方法［13］和ACF方法［14］分行业估算企业的全要素生产率，并采用门槛回归方法［9］支持了以上理论模型的推论，运用TOBIT回归分样本单独检验政府补贴对企业研发创新支出的影响。

本文的边际贡献在于：①将国际经济学领域的异质性企业理论［8］以及企业自选择问题运用于政府补贴、企业研发创新和生产率的研究中，深入分析了现实问题；②既有研究对门槛回归方法［9］的具体应用中，未充分诠释门槛值的理论含义，未充分界定作用方式发生转变的临界条件，而本文理论模型推导则为门槛回归方法的实际运用提供了扎实的理论基础，详细论述了双门槛、三区间差异化影响的形成机制，为每一个门槛值赋予了充分的理论含义，以弥补既有研究应用中缺乏清晰理论基础的不足。

1 文献述评

目前，既有研究对于政府补贴与我国企业研发创新和生产率提升的总体关系还没有明确统一的结论。任曙明和吕镯［5］对我国装备制造企业的研究发现，政府补贴冲抵了企业面临的融资约束，保证了企业生产率的平稳增长；白俊红［4］也发现我国政府的研发补贴能够促进企业的技术创新；而徐保昌和谢建国［6］、闫志俊和于津平［7］则实证发现，政府补贴抑制了企业的创新绩效和生产率提升。

此外，亦有研究也深入分析了不同情境和条件下政府补贴的差异化影响，试图以此揭示上述矛盾结论背后的成因，缺乏对差异化影响的讨论可能导致实证结果的不稳健，从而形成相互矛盾的结论。首先，政府补贴数额存在适度区间，过度高额补贴将抑制企业生产率的提升［15］。毛其淋和许家云［16］也发现了类似现象，政府补贴额度过低则无法达到企业进行研发创新的最低门槛，从而无法对企业新产品创新产生显著的激励作用；补贴额度过高却因寻租成本挤占了研发创新支出，则显著抑制了企业的新产品创新。其次，企业外部条件对政府补贴作用的发挥也具有关键影响。徐保昌和谢建国［6］研究发现，相对更优的政府质量能够显著提升政府补贴对企业生产率的促进作用。毛其淋和许家云［16］发现，地区层面更好的知识产权保护制度能够强化政府补贴对企业新产品创新的推动作用，而要素市场的扭曲则抑制了政府补贴对企业创新绩效的激励作用［17］。此外，当地经济发展水平、制度环境水平和要素禀赋水平也是重要的外部制约因素［18］。最后，企业内部条件的差异也不容忽视。白俊红［4］的研究表明，企业自身的知识存量、企业规模及产权类型均会对政府补贴效果产生影响。而杨洋等［17］则认为，由于国有企业和民营企业在资源禀赋和政府补贴的信号传递方面存在差异，政府补贴对这两类企业的创新绩效具有差异化影响。

已有的一些关于政府补贴影响企业生产率提升的作用机制研究，虽然总结了在不同的情境和条件下政府补贴对企业研发创新、生产率提升的差异化影响，但是这些分析都忽略了企业内部生产率的差异，而这正是影响企业利润和相关自选择的关键。若是忽视企业生产率的异质性，则难以全面、准确地描绘企业差异化的自选择以及政府补贴的双刃剑效应。广泛应用于国际经济学领域的异质性企业理论及其丰富成果则为该问题的研究带来了新视角，可以弥补以上研究不足。

既有研究从理论和实证层面研究了企业基于异质性生产率在出口行为上的差异化自选择，生产率更高的企业具有更大的规模和利润，能够克服相较国内市场更高的出口固定成本，因此具有更高的出口倾向［8，19］。BUSTOS［10］、ATKESON和BURSTEIN［20］将MELITZ［8］、MELITZ和OTTAVIANO［21］的基础模型框架中的企业外生生产率异质性拓展到企业可以通过研发创新投入实现内生生产率提升，这便刻画了企业除出口以外另一个差异化的自选择——研发创新，而这一自选择也依赖于企业既有的生产率。AW等［22-23］则从动态模型角度刻画了企业出口和研发创新的双重自选择，企业出口和研发创新的自选择基于既有的生产率，而当下出口和研发创新的自选择又会影响企业未来的动态生产率，这为研究企业的自选择行为提供了更加丰富的视角。

然而，目前并没有研究从异质性企业理论视角分析政府补贴对企业生产率的双刃剑效应，忽略了企业自选择的巨大作用，使得这一问题的研究尚有较大的拓展空间。不同企业即使接受了相同的政府补贴，也会根据自身利润最大化目标做出不同的决策，企业可以将政府补贴投入研发创新，也可以将之作为收益直接留存。唯有通过研发创新提升企业生产率之后企业增加的利润能够大于政府补贴，企业才会将其投入研发创新。企业接受政府补贴之后，政府补贴便成为企业研发创新的机会成本，生产率提升后利润增加便是潜在收益，机会成本和潜在收益之间的权衡是企业自选择的关键，企业权衡的基础是企业自身的既有生产率。而企业这一差异化的自选择直接决定了政府补贴能否发挥提升企业生产率的作用，缺少对这一作用机制的模型刻画，对于政府补贴和企业生产率之间的关系研究是一大缺憾。本文基于异质性企业模型框架分析不同生产率的企业对政府补贴的差异化使用，以及由此导致的政府补贴对企业生产率的双刃剑效应，并对相关理论模型推论做实证检验，力图弥补相关研究的空白。

2 理论模型

本文构建了同行业内基于产品差异化和CES效用函数的企业垄断竞争模型［24］，引入异质性企业的外生生产率差异［8］，拓展企业生产技术的自选择［10］，并考虑劳动单要素投入和企业生产的规模经济性［8，25］。

2.1 消费者需求端

2.2 企业生产端

2.2.1 政府补贴前 政府补贴前企业异质性的生产率为φ，这既是企业原始的外生生产率，也是企业经过研发创新在原始的外生生产率基础上获得提升的内生生产率。企业生产率φ直接决定了企业生产的所有企业面临相同的生产固定成本为f，企业生产的总成本函数为由企业利润最大化的边际成本加成定价可知，企业定价为，企业最大化收益r和利润π分别为：r=R(Pρφ)σ-1，显然，企业生产率越高，生产和销售规模以及利润也越大。

垄断竞争假设企业自由进入和退出，当企业利润π为负时，企业退出市场，由此可得企业幸存的门槛生产率φ*为生产率小于φ*的企业将被市场竞争淘汰。

2.2.2 政府补贴后 政府补贴只是针对行业总体中的少部分企业，对行业的总体变量Q、P和R并不会产生影响，这与垄断竞争的模型假设相一致［24］。

BUSTOS［10］用模型刻画了企业基于当下异质性的生产率做出差异化的技术选择：企业选择高技术，生产率从φ提升至γφ（γ＞1），相应的生产固定成本从f增加到ηf（η＞1）；而选择低技术的企业生产率和生产固定成本均不变。只有生产率提升带来的可变利润增加足以弥补生产固定成本的提高，企业才会选择新技术。为了与只有部分企业选择高技术的现实情况相符，BUSTOS模型假定η＞γσ-1，从而保证选择高技术的门槛生产率大于企业幸存的门槛生产率。

本文参考BUSTOS［10］对企业内生的技术自选择研究，但是将政府补贴下企业通过研发创新实现的生产率提升由γ和1之间的离散变化转变为关于政府补贴s的研发创新函数γ（s）＞1，γ（s）是关于政府补贴s的增函数。企业将政府补贴s用于研发创新后，生产率从φ提升至γ（s）φ。

企业将政府补贴s用于研发创新后的最大化利润表达式为显然，企业在政府补贴之前的既有生产率φ越高，利用政府补贴资金s进行研发创新后生产率提升带来的利润增长也越大。而企业将政府补贴s直接作为企业盈余的利润表达式为企业在选择政府补贴资金s的利用方式之前，需要权衡πRD和πs的大小。通过πRD（φRD）=πs（φRD），可以确定企业研发创新的门槛生产率当企业既有生产率φ高于研发创新的门槛生产率φRD时，πRD＞πs，企业将政府补贴资金s投入研发创新活动能够获得更大利润。

现实中并非所有幸存企业在得到政府补贴后都进行研发创新。根据中国工业企业数据库的统计，2007年共有40 840家企业获得政府补贴，但仅有9 908家企业的研发投入大于零，占比为24.26%，所以可以认为利用政府补贴从事研发创新活动并非所有幸存企业的选择。因此，与BUSTOS［10］模型设定相似，本文模型必须对相关参数做出限制，以保证研发创新门槛生产率φRD大于企业幸存门槛生产率φ*。结合上文的界定，可以发现，φRD＞φ*是否成立严格依赖于研发创新函数γ（s）的具体形式，如果少量的研发创新能够带来生产率的巨大提升，那么幸存企业必然都会利用政府补贴资金进行研发创新，此时φRD＜φ*，这显然与现实情况不符，因而可以合理假定研发创新函数γ（s）的具体形式能够保证φRD＞φ*成立。

2.3 政府补贴的双刃剑效应

图1呈现了异质性企业基于政府补贴前既有异质性生产率做出不同的自选择，以及由此政府补贴对异质性企业的双刃剑效应。图1中灰色直线（实线部分）代表政府补贴前幸存企业的利润，黑色折线（实线部分）代表政府补贴后幸存企业的利润，企业针对政府补贴做出何种自选择，政府补贴都增加了其实际利润，而生产率大于研发创新门槛生产率φRD的企业利润增加幅度更大，且随政府补贴前的企业既有生产率递增。这源自于企业差异化的自选择。

图1 政府补贴的双刃剑效应分析Fig.1 Double-edged-sword effectsofgovernmentsubsidy

政府补贴前生产率大于φRD的企业，将政府补贴资金s投入研发创新的利润πRD大于将s直接作为企业盈余的利润πs，因此企业会选择研发创新以获得更大的利润，而且两种选择之间的利润差异随着企业生产率的提高而增大，在图1中体现为第1区间中直线πRD和直线πs的差异。

政府补贴前生产率小于φRD的企业，研发创新的利润πRD小于将s直接作为企业盈余的利润πs，且两者之间的利润差异随着企业生产率的降低而扩大，表明生产率越低的企业越倾向于将政府补贴直接作为企业盈余留存，在图1中体现为第2～4区间中直线πRD和直线πs的差异。

政府补贴前生产率小于φ*的企业，即原先应当被市场竞争所淘汰的落后企业，由于政府补贴资金s弥补了亏损，实际的企业幸存门槛生产率降低至

生产率小于φ*但大于φs的落后企业通过政府补贴得以幸存，在图1中体现为第3区间中直线πs和直线π的差异。而生产率处于图1中第4区间的企业（φ＜φs）由于政府补贴无法弥补原先的亏损，因而依旧被市场竞争淘汰。

因此，政府补贴针对不同生产率的企业形成了双刃剑效应。对于生产率较高（φ＞φRD）的企业，政府补贴推动了企业研发创新，从而促进了企业生产率提升，更高的政府补贴s将带来更大幅度的生产率提升；而对于生产率较低（φ＜φ*）的企业，政府补贴则扰乱了市场竞争之下正常的淘汰机制，导致落后企业“僵而不死”，更多的政府补贴只会挽救生产率更低的落后企业，从而在数据上表现为政府补贴与企业生产率之间的负向关系，即政府补贴“阻碍”了企业生产率提升；对于生产率处于中游（φ*＜φ＜φRD）的企业，由于自身的生产和销售规模有限，通过研发创新提升生产率、降低生产的边际成本并不是企业的最优选择，因而政府补贴不影响企业生产率提升。

3 实证检验

依据上文理论模型的推论，将实证检验政府补贴究竟促进还是阻碍了企业生产率提升。首先，为了保证估计结果的一致性和稳健性，分别采用LP方法和ACF方法计算企业的全要素生产率。其次，利用门槛回归方法［9］估计政府补贴对企业生产率产生差异化影响的生产率门槛值（企业幸存门槛生产率φ*和研发创新门槛生产率φRD），分析生产率在不同区间时政府补贴的双刃剑效应。最后，利用门槛回归方法分析政府补贴对企业研发创新支出的差异化影响，并利用TOBIT回归分样本单独检验政府补贴的影响，以此继续佐证文章的推论。

3.1 数据和变量

本文的实证检验采用中国工业企业数据库1998—2007年为期10年的数据③为了保证估计的稳健性、捕捉现阶段的新特征，本文也采用了1998—2013年的数据对部分回归结果进行稳健性检验，但估计结果并未发生实质性变化，限于文章篇幅，故这部分结果不再呈现。由于2008—2013年部分年份以及部分变量的数据缺失，且本文采用的门槛回归方法要求使用平衡面板以及我国企业剧烈的进入退出特征，延长样本数据的时间跨度也将导致可用于计量分析的企业数量急剧减少，为了使得本文的计量结果更具代表性及可靠性，本文在文章主体部分采用1998—2007年数据。，只选取制造业企业作为研究对象，即两位数产业代码为13～42的企业。参照BRANDT等［26］的方法将截面数据拼接为面板数据。对于部分年份缺失的工业增加值，借鉴刘小玄和李双杰［27］、聂辉华等［28］的方法，根据会计准则间接计算得到。此外，根据BRANDT等［26］和杨汝岱［29］的方法，利用既有的企业固定资产原值数据计算企业每年真实资本存量，并利用产出平减指数和投入平减指数计算真实工业增加值和真实中间品投入量。最后，根据既有研究的通用标准剔除异常观测值。门槛回归方法要求平衡面板数据，剔除了生产率的极端值及控制变量的缺失值后，最终获得由17 639家企业构成、为期10年的平衡面板数据。

利用索洛余值思想计算企业的全要素生产率：yit=β0+βllit+βkkit+φit+ηit。其中，劳动力投入lit和资本存量kit对企业工业增加值贡献的剩余φit就是企业的全要素生产率。OLLEY和PAKES［30］利用企业投资iit=i（φit，kit）近似企业生产率φit=h（iit，kit），且Φit（iit，kt）=βkkit+h（iit，kit），并采用两阶段估计解决了企业生产投入和企业生产率之间的同步偏误导致的生产投入要素变量的内生性问题。LEVINSOHN和PETRIN［13］进一步指出，由于数据中企业投资存在大量零值以及企业投资并不一定对企业生产率变动做出充分反馈，采用企业中间品投入mit=m（φit，kit）近似估算企业生产率φit=g（mit，kit）更为合适。ACKER-BERG等［14］研究发现，如果劳动力投入lit也为生产率φit和资本存量kit的函数，那么lit=［g（mit，kit），kit］将与Φit（mit，kit）=βkkit+g（mit，kit）产生完全共线性，导致第一阶段估计中劳动力投入lit的系数不可识别。ACF方法假定企业中间品投入mit条件依赖于劳动力投入lit，将企业中间品投入的函数修改为mit=f（φit，kit，lit），通过在第二阶段估计所有参数，解决了第一阶段中劳动力投入系数不可识别的问题。

企业的全要素生产率是本文的核心变量。为了保证实证结果的一致性和稳健性，本文同时选用LP方法和基于LP方法进行的ACF方法估算企业的全要素生产率。考虑不同行业的生产函数存在差异，本文参考BRANDT等［26］和杨汝岱［29］的做法，按两位数产业代码分行业估算企业的全要素生产率。最后，为了避免生产率的极端值对估计结果产生影响，本文剔除了生产率前后各1%的观测值极端值。所有企业全要素生产率的整体情况如表1所示。

表1 企业全要素生产率的整体情况Tab.1 Description of firm’s TFP

表2列出了计量模型中使用的所有变量的定义和基本统计信息。

表2 变量定义及基本统计信息Tab.2 Definition and statistic information of the variables

3.2 政府补贴对企业生产率的差异化影响

3.2.1 计量模型构建 既有研究［23，31］表明，企业的研发创新投入对于企业生产率提升存在明显的滞后效应。因此，企业将政府补贴投入研发创新也同样存在对生产率提升的滞后效应，选择政府补贴的滞后一期作为核心解释变量更为合理。此外，企业生产率的控制变量选取参考相关研究［15，18］。构建的基础计量模型如下。

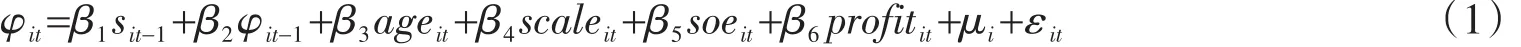
其中：核心解释变量sit-1为滞后一期的政府补贴；被解释变量φit为当期的企业生产率；控制变量包括企业年龄ageit、企业规模scaleit、企业性质soeit、企业盈利能力profitit、滞后一期的企业生产率φit-1；μi表示不可观测且与企业个体相关的非时变变量；εit为模型残差。

根据上文的理论模型，滞后一期的政府补贴sit-1对当期企业生产率φit存在双刃剑效应。与政府补贴同期的企业生产率大于研发创新门槛生产率（φit-1＞φRD）时，企业将政府补贴sit-1用于研发创新，进而提高了企业生产率φit；小于企业幸存门槛生产率（φit-1＜φ*）时，政府补贴sit-1只是挽救了原先应当被淘汰的低生产率企业，给予更多的政府补贴只会挽救生产率更低的企业；小于研发创新门槛生产率且大于企业幸存门槛生产率（φ*＜φit-1＜φRD）时，企业只是将政府补贴作为留存收益，而不会用于研发创新活动。因此，基础计量模型可以进一步拓展为分段函数形式。

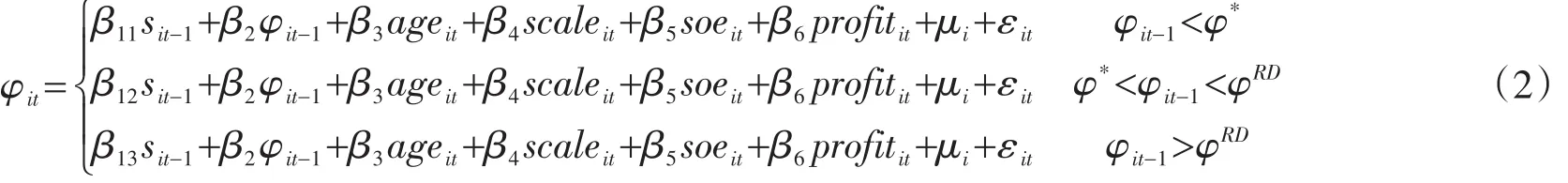
根据滞后一期企业生产率φit-1的所处区间，政府补贴sit-1对企业生产率φit的影响系数β1可以细分为β11（φit-1＜φ*）、β12（φ*＜φit-1＜φRD）以及β13（φit-1＞φRD），而控制变量的影响系数不发生变化。依据理论模型的推论，系数β11（φit-1＜φ*）应当显著为负，系数β12（φ*＜φit-1＜φRD）应当不显著，系数β13（φit-1＞φRD）应当显著为正，从而形成双门槛、三区间的差异化影响。后续实证检验需要估计政府补贴sit-1差异化的影响系数β11～β13、控制变量的影响系数β2～β6以及企业幸存门槛生产率φ*和研发创新门槛生产率φRD。

3.2.2 门槛回归方法 HANSEN［9］的门槛回归方法符合上文计量模型估计的需要。分段函数形式的计量模型（2）可以简化为

3.2.3 门槛效应检验 HANSEN［9］利用似然比统计量检验门槛效应的显著性。在原假设“H0：不存在企业幸存门槛生产率φ*或研发创新门槛生产率φRD”下，得到受约束的残差平方和；在备择假设“H1：存在企业幸存门槛生产率φ*和研发创新门槛生产率φRD”下，得到无约束的残差平方和。受约束残差平方和与无约束残差平方和之差越大，则似然比统计量越大，越倾向于拒绝原假设。在HANSEN［9］和WANG［32］的实际操作中分别依次检验单门槛效应、双门槛效应和三门槛效应的显著性，即原假设分别依次为“H0：不存在单门槛效应”“H0：不存在双门槛效应”以及“H0：不存在三门槛效应”，并根据门槛效应的检验结果选择最合适的门槛数。针对本文的研究，需要着重关注双门槛模型（即企业幸存门槛生产率φ*和研发创新门槛生产率φRD）能否得到检验支撑。此外，由于似然比统计量的渐进分布并非标准的χ2分布，门槛效应检验利用自助法（bootstrap）模拟似然比统计量的渐进分布。

本文利用WANG［32］提供的Stata程序进行相关计算和检验，分别搜寻300个样本点估计企业幸存门槛生产率φ*和研发创新门槛生产率φRD，并利用自助法（bootstrap）反复抽样300次用于检验门槛效应显著性的似然比统计量的渐进分布。表3呈现了门槛效应检验的结果。

表3 门槛效应检验Tab.3 Threshold effect test

从表3可知，无论是基于LP方法还是ACF方法测度的企业全要素生产率，单门槛检验和双门槛检验的p值均为0.000，表明显著的拒绝原假设“H0：不存在单门槛效应”和“H0：不存在双门槛效应”，即至少存在2个门槛；而三门槛检验的p值分别为0.523和0.840，这表明无法显著拒绝原假设“H0：不存在三门槛效应”，即应当接受不存在3个门槛的原假设。因此，根据门槛效应的检验结果，选择双门槛模型最为合理的，这与上文理论模型的推论高度契合，双门槛模型既有理论层面的推导，也有实证层面的支撑。

3.2.4 门槛值的置信区间 确定采用双门槛模型后，需要进一步分析估计的门槛值（即企业幸存门槛生产率φ*和研发创新门槛生产率φRD）的精确性和稳健性。

依据HANSEN［9］的方法，在原假设“H0：选取的门槛值为真实门槛值”下分别构建关于2个门槛值的似然比统计量，似然比统计量的渐进分布虽然是非标准的，但可知其累计分布函数为因而，可以直接计算各个置信度下的临界值以及企业幸存门槛生产率φ*和研发创新门槛生产率φRD在各个置信度下的置信区间。置信区间越小，表明在该置信度下对真实门槛值的潜在选择区间越小，即表明通过双门槛模型估计的门槛值具有越高的精确性和稳健性。

图2分别呈现了基于LP方法和ACF方法测度生产率的企业幸存门槛生产率φ*和研发创新门槛生产率φRD在95%置信度下的置信区间，图中实线表示在门槛生产率的各种选择之下相应的似然比统计量的数值，虚线表示95%置信度下似然比统计量的数值，处于虚线以下的实线部分便是各个门槛生产率的置信区间。从图2可以看出，各个门槛生产率95%的置信区间都比较狭小，置信区间以外的似然比统计量均明显大于95%置信度的临界值7.35，这表明估计的门槛值具有比较高的精确性和稳健性。表4提供了门槛值及其95%置信度的置信区间上下界的详细信息，基于LP方法测度生产率的双门槛值分别为4.927和7.342，基于ACF方法测度生产率的双门槛值分别为2.914和4.804，且其置信区间跨度比较小，均维持在0.1个标准差左右。

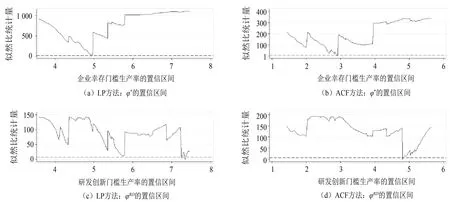
图2 利用LP方法和ACF方法测度生产率的双门槛置信区间Fig.2 Confidence intervalof threshold TFPmeasured by LPmethod and ACFmethod

表4 门槛值的置信区间Tab.4 Confidence intervalsof threshold values

3.2.5 门槛模型的回归结果 本研究关注的是核心解释变量滞后一期的政府补贴sit-1对当期企业生产率φit的影响，结果见表5。式（1）的基础回归模型和式（3）的门槛回归模型得出了截然不同的结果，这是因为式（1）的基础回归模型忽略了政府补贴对企业生产率的双刃剑效应。表5中的第2列和第3列呈现了全样本的sit-1对φit的影响，sit-1的影响系数非常小且极不显著，从总体上看政府补贴对企业生产率并不产生影响。但在第4列和第5列呈现的门槛回归模型的结果中，却可以发现完全不同的现象，滞后一期的政府补贴sit-1对当期企业生产率φit并非没有影响，而是根据滞后一期的企业生产率φit-1所处水平的不同形成了差异化的影响：①当滞后一期的企业生产率φit-1小于企业幸存门槛生产率φ*时，滞后一期的政府补贴sit-1对当期企业生产率φit产生了显著的抑制作用，根据上文的理论模型推导，这实际上并不是政府补贴对企业生产率产生了直接抑制作用，而是政府补贴挽救了原先在市场竞争中应当被淘汰的生产率落后企业所致，更多的政府补贴只会挽救生产率更低的企业，这在数据层面表现为政府补贴显著抑制企业生产率提升；②当滞后一期的企业生产率φit-1大于企业幸存门槛生产率φ*且小于研发创新门槛生产率φRD时，政府补贴既不会影响企业原先在正常市场竞争机制中的优胜劣汰，也不会影响企业的研发创新决策，所以在回归结果中表现为sit-1对φit的影响极其微弱且极不显著；③当滞后一期的企业生产率φit-1大于研发创新门槛生产率φRD时，企业因较高的既有生产率而具有较高的销售收入、市场份额和利润，更倾向于将政府补贴用于研发创新活动，从而提高了企业在下一期的生产率，所以滞后一期的政府补贴sit-1对当期企业生产率φit的提升产生了显著的促进作用。当计量模型的门槛效应被忽略时，φit-1＜φ*时政府补贴对企业生产率的负向影响与φit-1＞φRD时政府补贴对企业生产率的正向影响同时存在，这而使得式（1）基础回归模型的结果从整体层面掩盖了这些差异化的影响，仅表现为政府补贴对企业生产率没有显著影响，因此，无论从理论层面出发还是实证层面出发，关注企业生产率的门槛值并据此进行分类讨论极为必要。门槛回归模型的结果与上文理论模型的推导完全契合，两者互为印证。从定量角度看，政府补贴对企业生产率负向影响系数的绝对值大于正向影响系数的绝对值，这表明从社会整体生产率来看，政府补贴的负面影响幅度要大于正面影响，这更提醒政府补贴应当审慎而为。

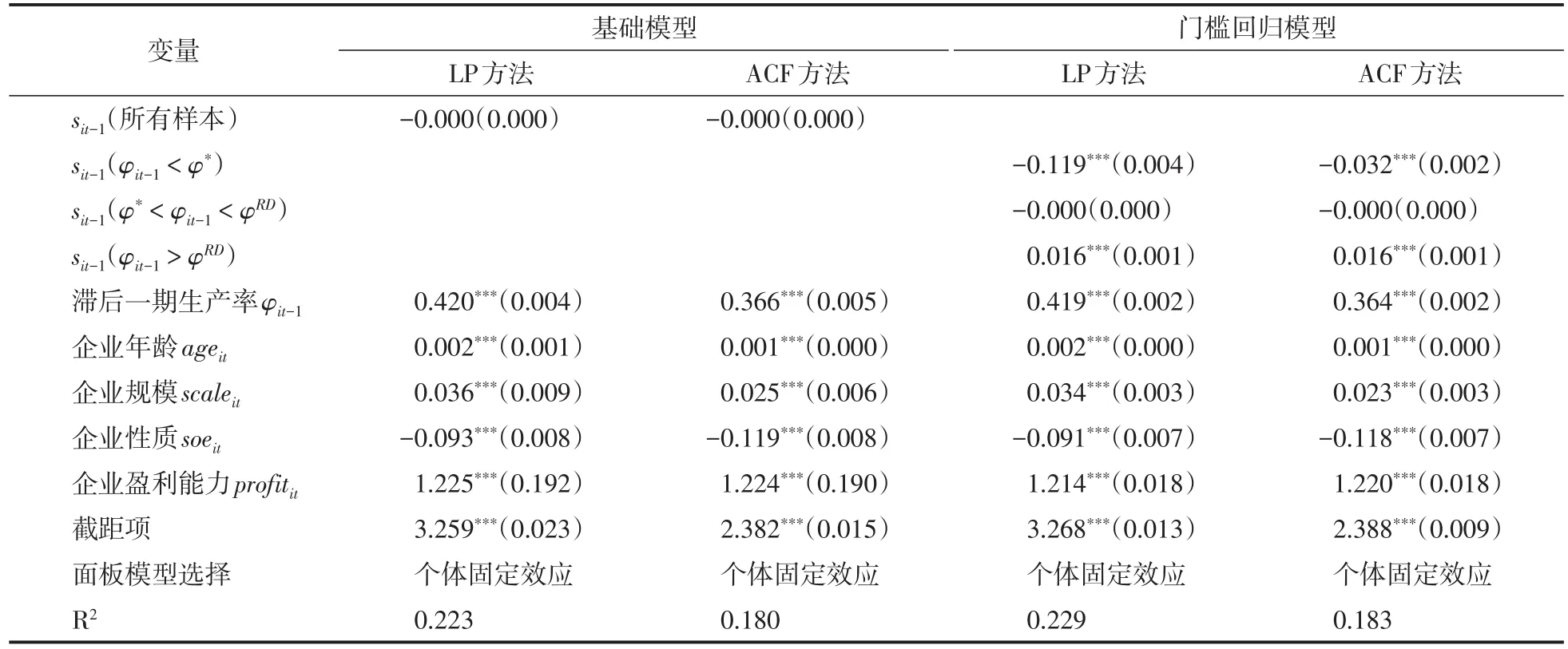
表5 政府补贴对企业生产率影响的回归结果Tab.5 Regression resultsof impactsofgovernmentsubsidy on firms’TFP

控制变量方面，衡量企业性质的虚拟变量对企业生产率产生了高度显著的负向影响，这表明相较于非国有企业而言，国有企业的生产率明显更低，这与BRANDT等［26］和杨汝岱［29］对我国企业生产率的对比分析得出的结论相一致。

模型的稳健性方面，无论是基础模型还是门槛回归模型，无论是基于LP方法测度的企业生产率还是基于ACF方法测度的企业生产率，模型核心解释变量和控制变量影响系数的符号、数值以及标准误均没有明显差异，因此可以认为上述计量模型的估计结果是稳健的。

3.3 政府补贴对企业研发创新的差异化影响

根据上文的理论模型，政府补贴对企业生产率形成双刃剑效应的关键在于企业会根据自身既有生产率水平对政府补贴做出差异化自选择，即只有处于研发创新门槛生产率φRD以上的企业才会将政府补贴用于研发创新。为此，有必要进一步检验企业针对政府补贴的差异化自选择是否成立。中国工业企业数据库2005—2007年的数据包含了企业的研发创新支出，恰可以利用这个子样本实证检验政府补贴对企业研发创新支出的差异化影响，从而验证企业差异化的自选择行为。依据上文理论模型的推论，利用门槛回归方法，构建计量实证模型如下。

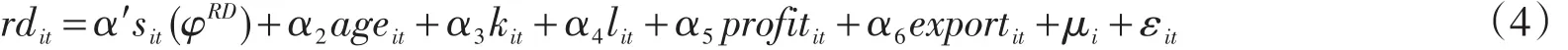
限于文章篇幅，直接在表6呈现基于ACF方法计算企业生产率的计量模型的回归结果，不再给出门槛效应检验和门槛值置信区间估计的结果。利用门槛回归方法估计的研发创新门槛生产率φRD为4.893。表6的第2列呈现单门槛回归模型的计量结果。根据估计的研发创新门槛生产率将全样本划分为2个子样本（φit＜φRD和φit＞φRD），在不同企业生产率水平下估计政府补贴对企业研发创新支出的影响，并且分别利用OLS回归和TOBIT回归对2个子样本分别进行单独回归，表6的第3列和第4列呈现了对子样本OLS回归的结果，第5列和第6列呈现了对子样本进行TOBIT回归的结果。

表6 政府补贴对企业研发创新支出的差异化影响Tab.6 Heterogeneous impactsofgovernmentsubsidy on firms’R&D

理论上，对于将政府补贴全部用于研发创新支出的企业而言，政府补贴前既有的研发创新支出体现在模型的残差项和截距项中，理想情况下政府补贴sit对企业研发创新支出rdit的影响系数应当显著地接近1。如果企业不将政府补贴用于研发创新支出，那么政府补贴对于企业研发创新支出就没有影响，理想情况下在计量回归结果中应当体现为政府补贴sit的影响系数接近0。事实上，计量实证检验的结果与理论预期基本一致。当φit＜φRD时，政府补贴sit门槛回归的估计系数为-0.022，子样本OLS回归的估计系数为-0.012，子样本TOBIT回归的估计系数为0.010，影响系数均接近于0；当φit＞φRD时，政府补贴sit门槛回归的估计系数为1.043，子样本OLS回归的估计系数为1.195，子样本TOBIT回归的估计系数为1.296，影响系数均接近于1且高度显著。因此，根据对政府补贴影响企业研发创新支出的实证检验，本文认为企业对于政府补贴根据自身既有生产率的不同做出了差异化的自选择，只有生产率较高的企业（φit＞φRD）才会利用政府补贴进行研发创新，而对于生产率较低的企业（φit＜φRD），政府补贴对其研发创新活动并没有影响。

4 结论与政策启示

MELITZ［8］的异质性企业模型将行业内的人均社会福利表达为行业的总体生产率水平，而行业的总体生产率水平又取决于优胜劣汰的市场竞争机制，唯有激发市场活力、促进企业优胜劣汰，才能提高行业总体生产率和人均社会福利水平。政府补贴的宗旨必然是社会福利的最优化，而其对企业生产率的影响恰是最合适的分析切入点，“优胜”和“劣汰”则是两个重要的分析维度，即政府补贴对原先生产率优势企业和劣势企业分别产生了怎样的影响。

本文基于MELITZ［8］异质性企业模型和BUSTOS［10］的企业研发创新自选择模型，构建了理论模型分析企业针对政府补贴的差异化自选择，并由此分析政府补贴对企业生产率的双刃剑效应。政府补贴效果能否发挥的关键在于企业对政府补贴的利用方式，而这又取决于企业的收益权衡，只有既有生产率大于研发创新门槛生产率的企业，才能基于既有更大的销售收入和市场份额，通过研发创新提升生产率来获得相较于政府补贴更大的收益，除此以外的企业，政府补贴对其研发创新活动和生产率提升不会产生影响。因此，在“优胜”维度，政府补贴发挥了积极正面的作用，帮助一部分既有生产率较高的企业提升生产率；但在“劣汰”维度，政府补贴则阻碍了原先的生产率劣势企业被市场竞争淘汰，挽救了既有生产率小于企业幸存门槛生产率的落后企业。

理论模型中，根据企业既有生产率水平的分段影响机制恰好与门槛回归方法高度契合。对理论模型而言，采用门槛回归方法是对其进行检验支撑的最优方法；对门槛回归方法而言，本文的理论模型推导为其提供了扎实的理论基础，对门槛值的产生与含义给予了充分的理论诠释，丰富了门槛回归方法的应用。

门槛回归方法的计量结果支持了理论模型的推论。对于既有生产率大于研发创新门槛生产率的企业，政府补贴推动企业研发创新活动，从而提高了企业的生产率（促进“优胜”）；对于既有生产率小于企业幸存门槛生产率的企业，政府补贴使其得以继续生存，更多政府补贴只会挽救生产率更低的企业，从而在计量结果中表现为政府补贴显著抑制了企业生产率提升（阻碍“劣汰”）；对于既有生产率介于两者之间的企业，政府补贴不影响其研发创新，进而不影响其生产率提升。

既然政府补贴对企业生产率的影响是利弊共存，相应地，政府提供补贴就必须审慎而为、扬长避短。政府应当仔细甄别高生产率企业，仅为其提供补贴，帮助其在资金实力有限的情况下开展研发创新活动，以更高的生产率获得更大的竞争优势。在供给侧结构性改革的背景下，为了实现“加强优质供给，扩大有效供给，提高全要素生产率”的改革目标，政府补贴应当有所作为，以受益于研发创新的正外部性。如若政府对于补贴对象筛选不当，给予既有生产率较低的企业以政府补贴，非但无法实现以补贴促进研发创新的初衷，还扰乱了市场竞争机制下企业间正常的优胜劣汰，使得并不具备竞争优势、理应被淘汰的劣势企业“僵而不死”，导致困扰已久的“僵尸企业”问题与“去产能，减少无效供给”的改革目标背道而驰。

最后，政府基于高生产率企业更强的研发创新意愿进行择优补贴、锦上添花的同时，小微企业的生存和发展问题也不容忽视，部分处于初创期的小微企业在短期内无法充分释放其竞争潜力，因而机械地将全要素生产率作为对其竞争优势的唯一衡量标准并不合适，对创业团队的客观评估、对创业项目的理性预测、对目标市场的深入研究等都应当构成对其全面考量的基础。然而，由于初创期小微企业的各项信息和发展前景难以准确甄别和预测以及我国风险投资行业正在快速发展，相较于逐利而为的市场资本以及具有丰富业界经验的职业投资人，政府并不具有充分的动力和能力来更好地实现前期信息甄别以及后期控制监督，政府补贴反而可能滋生寻租腐败，浪费社会资源。因此，市场和政府应当合理分工，发挥各自所长，对于市场资本活跃的产业应交由市场实现优胜劣汰，而对于发展路径明确但周期长、投资大且涉及国计民生的关键产业和企业，政府可以弥补市场不足，以合理补贴推动创业创新、实现经济的长期可持续发展。