螺旋管式直流蒸汽发生器建模仿真与控制
2020-03-11张月郑明光马志才吴建邦
张月,郑明光,,马志才,吴建邦
1.上海核工程研究设计院有限公司,上海200233
2.上海交通大学核科学与工程学院,上海200240
螺旋管式直流蒸汽发生器由于体积小、换热效率高等特性[1-2],是一体化反应堆重要设备之一。为研究一体化反应堆的仿真系统及控制方法,需要建立螺旋管式直流蒸汽发生器的动态模型[1-8]。另外,由于螺旋管式直流蒸汽发生器二回路水容积小,蒸汽流量变化过程中蒸汽压力极易发生变化,且若给水跟不上,很容易对二回路设备造成影响[9],因此需要对螺旋管式直流蒸汽发生器开展控制方案研究,以保证二次侧蒸汽出口压力恒定。
本文将螺旋管式直流蒸汽发生器分为一次侧、金属管壁、二次侧3个部分,每个部分基于移动边界理论,将整个轴向分为过冷段、两相段、过热段3个部分,结合每段的质量、能量、动量三大守恒方程,给出了螺旋管式直流蒸汽发生器的状态方程。以国际革新与安全反应堆(IRIS)为参考对象,进行稳态计算和动态仿真实验。当蒸汽流量变化时,蒸汽发生器蒸汽出口压力发生变化,此时蒸汽发生器蒸汽出口压力的偏差作为PID控制器的输入,进而改变给水流量,从而使蒸汽出口压力回到给定值范围内。
1 物理模型
根据螺旋管内流体的流动换热过程,对螺旋管式直流蒸汽发生器模型做如下假设:1)由于螺旋管直流蒸汽发生器结构复杂,在建立热工水力数学模型时可忽略对热工特性影响较小的结构,主要分析一次侧冷却剂与螺旋管内二回路工质在螺旋管区域热交换过程,未考虑蒸汽发生器进出口直管段换热以及其他热损失;2)在建立模型时,假设一次侧工质不发生相变,为单相液流动;3)将螺旋管做单管模型处理,等效方法如下:总质量流量为单根螺旋管的质量流量与螺旋管数目的积,总流通面积为单根螺旋管的流通面积与螺旋管数目的积,总换热面积为单根螺旋管的换热面积与螺旋管数目的积;4)使用一维模型,忽略轴向导热;5)一次侧密度沿着轴向维度不发生变化;6)一次侧不考虑轴向压降,且压力沿着时间维度保持不变;7)忽略金属管壁密度的变化;8)一次侧不考虑控制体外部压力做功。
基于以上假设,根据二次侧工质的状态,将蒸汽发生器分为一次侧、金属管壁、二次侧3部分。基于可移动边界理论,将二次侧沿轴向管长分为3个区域,即过冷段ssc、两相段ssb和过热段sss;同理将一次侧分为pⅠ、pⅡ、pⅢ共3个区域,金属管壁分为mⅠ、mⅡ、mⅢ这3个区域。相应划分情况示如图1所示。

图1 螺旋管式直流蒸汽发生器节点划分示意
在图1中,二次侧过冷段为1~3区域、两相段为3~5区域、过热段为5~7区域,其中1、3、5、7为各段边界,2、4、6为各段控制体中心代表点,3为饱和液相点,5为饱和汽相点。
2 数学模型
2.1 基本方程
螺旋管式直流蒸汽发生器是由很多根螺旋管并联组成的表面换热设备。二次侧管内工质在流动时,不断地吸热,导致热力状态发生变化,基本的质量、能量和动量三大守恒方程为
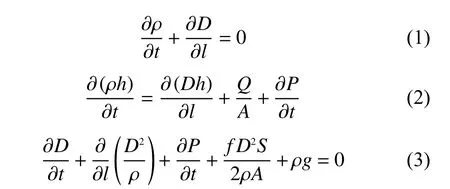
式中:ρ为流体密度;D为单位面积质量流速;h为流体比焓;Q为单位长度热流率;A为流通面积;P为流体压力;f为摩擦系数;g为重力加速度。
2.2 可移动边界理论
设控制体流通面为单位面积A,j、j+1分别为上、下边界的节点,上界面为Zj+1,下界面为Zj,ρ为控制体内物质密度,W为通过界面的质量流量,L为控制体的长度,h、P为控制体内流体比焓和流体压力,S为源项,可移动边界理论示意如图2所示。
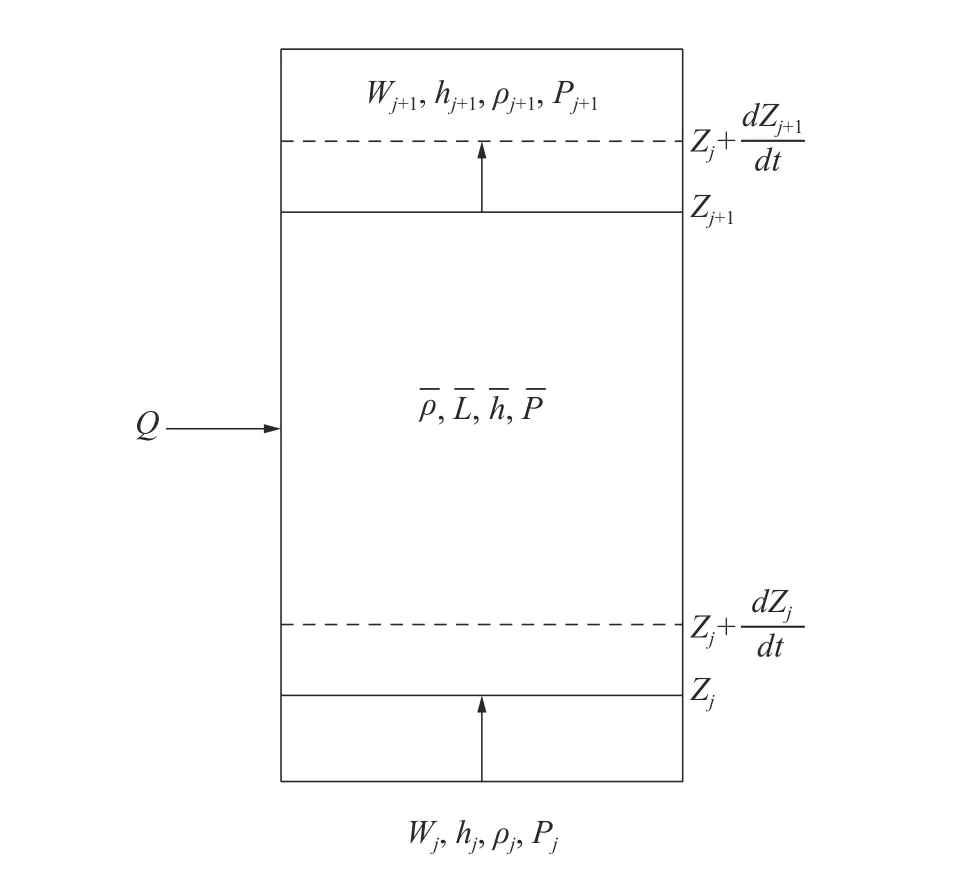
图2 可移动边界理论示意

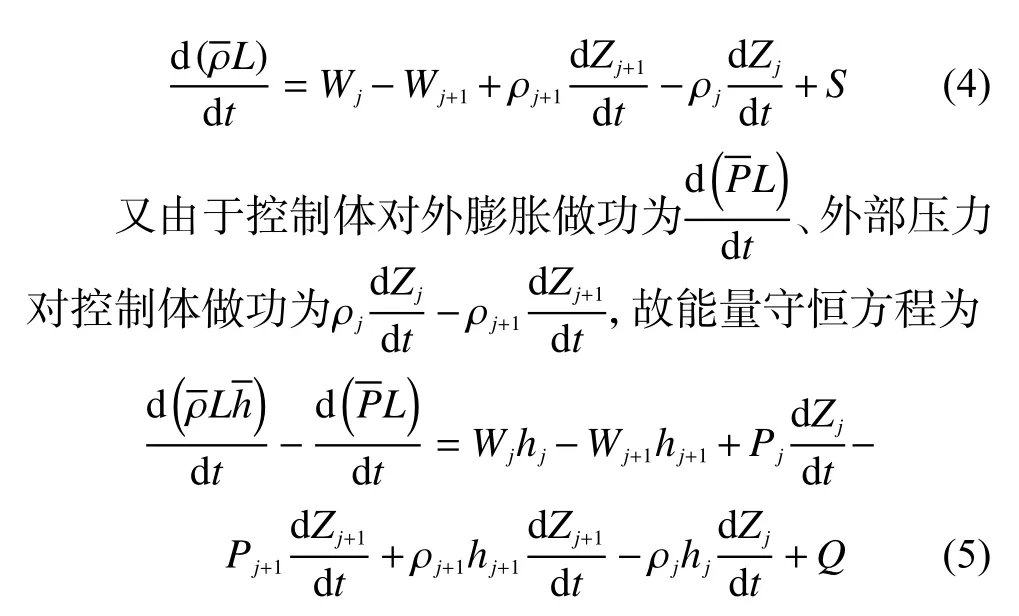
2.3 一次侧热动力学方程

2.4 金属管壁热动力学方程
金属管壁侧分为3个节点,利用可移动边界法,在推导出每个金属管壁节点能量方程时,必须考虑由于边界移动引起的能量传递。图3为金属管壁的节点能量传递图。

图3 金属管壁节点能量传递

2.5 二次侧热动力学方程



2.6 状态方程模型

3 模型仿真
3.1 稳态特性计算
为了检验模型的正确性和适用程度,根据IRIS的设计和运行参数,使用Matlab程序语言SIMULINK 仿真系统,构建仿真计算平台,对模型进行稳态结果和动态结果的检验。稳态结果可以和已有的稳态设计数据进行定量比较,文献[1,12]给出了IRIS在100%负荷工况下的稳态设计值,将此作为模型稳态检验的基础,以文献中的结果为参考值,进行模型稳态结果的定量检验。对于形式如式(24)的动态特性方程,因为在稳定状态时x˙是零向量,故可利用求解方程组F(x,u)=0,从而得到稳定状态时的状态量x。

表1 稳态计算结果分析对比
3.2 动态特性计算
为验证模型的动态特性,本文进行了阶跃仿真实验。
考察第1个典型的动态工况:在100%额定负荷下,保持一次侧流量、一次侧压力、一次侧入口温度、二次侧给水温度和焓值以及蒸汽调节阀开度等输入参数不变,二次侧给水流量阶跃减小5%,系统状态量变化如图4所示。
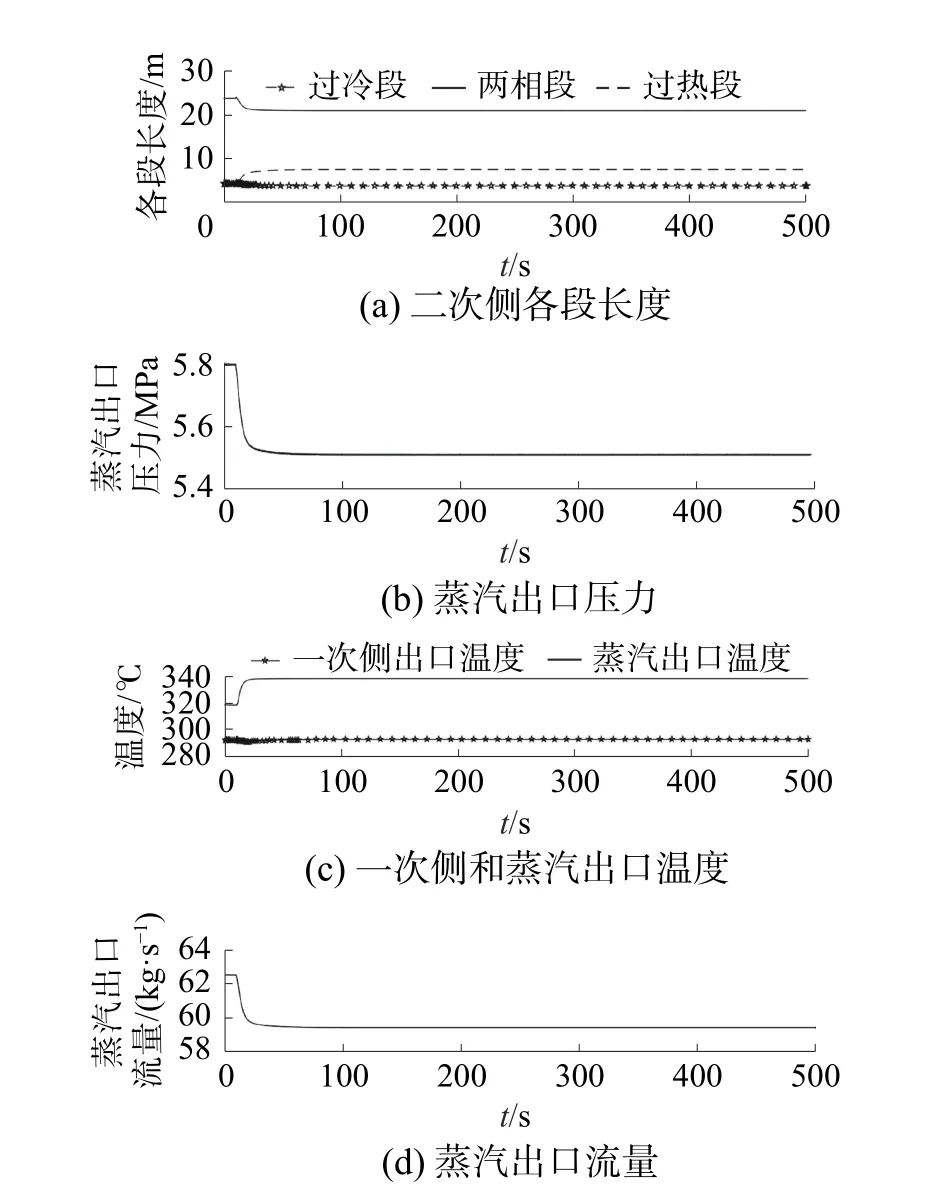
图4 二次侧给水流量扰动下的瞬态特性曲线
瞬态开始时,二次侧流量阶跃降低,此时一次侧与二次侧的换热并不会瞬间降低,即二次侧的吸热能力并不会瞬间降低。根据能量守恒定理Q=cmΔt可知,m在减小,Q保持不变,故二次侧进出口温差Δt增加,所以二次侧出口温度增加。随着时间的推移,流量降低到一定程度并且稳定下来,流量的降低,使得二次侧换热系数减少,进而使得一、二次侧的换热量减少,一次侧出口温度增加;二次侧给水加热到饱和水和饱和蒸汽所需的热量减少,使得过冷段和两相段的长度减小,过热段长度增加。由于过热段长度的增加使得二次侧出口蒸汽温度升高。由于进出口质量守恒,所以二次侧给水流量和出口蒸汽流量相等,进而由式(23)可知,蒸汽出口压力与蒸汽流量成正比,出口压力会降低。
当系统各参数经过100 s的瞬态后,一次侧和二次侧的能量再次达到平衡,各出口参数重新稳定在一个新的水平上。
考察第2个典型的动态工况:在100%额定负荷下,保持一次侧入口温度、一次侧压力、二次侧给水流量、二次侧给水温度和焓值以及蒸汽调节阀开度等输入参数不变,在10 s时,一次侧入口流量阶跃增加10%,观察系统状态参数的如图5 所示变化。
瞬态开始时,一次侧流量阶跃增加,但是此时一次侧与二次侧的换热并不会瞬间增加,即二次侧的吸热能力并不会瞬间增加。根据能量守恒定理可知,一次侧流量在增加,热量保持不变,故一次侧进出口温差降低,所以一次侧温差减小,一次侧出口温度增加。随着时间的推移,流量增加到一定程度,并且稳定下来,流量的增加使得一次侧传热系数增加,进而使得一、二次侧的换热量增加,过热段长度增加,过冷段和两相段的长度减小。由于过热段长度的增加使得二次侧出口蒸汽温度升高;由于两相段长度的减少使得二次侧压降降低。

图5 一次侧入口流量扰动下的瞬态特性曲线
当系统各参数经过100 s的瞬态后,一次侧和二次侧的能量再次达到平衡,各出口参数重新稳定在一个新的水平上。
4 控制系统仿真
4.1 控制器设计
本文采用PID控制器建立螺旋管式直流蒸汽发生器蒸汽出口压力控制系统。当改变蒸汽出口流量时,通过调节二次侧给水流量来保证蒸汽出口压力恒定,给水流量调节的输入信号是蒸汽出口压力的偏差。
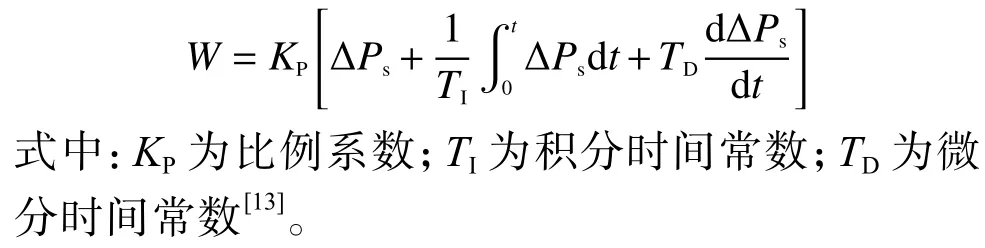
由于螺旋管式直流蒸汽发生器二回路水容积小,因此蒸汽流量变化过程中,蒸汽压力极易发生变化,且若给水跟不上,很容易对二回路设备造成影响。因此,为快速响应蒸汽流量的变化,本文提出用蒸汽压力偏差信号和蒸汽流量信号对二次侧给水流量进行调节。其中,蒸汽压力偏差信号为主控信号,蒸汽流量作为辅控信号,共同调节给水流量。控制器结构如图6所示。需求给水流量表达式为


图6 控制器结构
4.2 控制器仿真结果
在100%额定负荷下,保持一次侧入口温度、一次侧压力、一次侧流量、二次侧给水流量以及二次侧给水温度和焓值等输入参数不变,前10 s为满功率稳态运行;在10 s时,给蒸汽调节阀开度斜坡输入,令变化速率为1%/s,使得在90 s时完成把蒸汽调节阀开度线性降低为满功率时的20%。由式(23)可知,蒸汽调节阀开度与蒸汽流量成正比,故有蒸汽流量线性降低为满功率的80%,此时控制仿真结果如图7所示,最终蒸汽出口压力可以稳定到所要的值5.8 MPa。

图7 控制仿真结果
当蒸汽出口流量降低时,蒸汽温度和蒸汽压力会升高。此时,二次侧从一次侧带走的热量减少,一次侧出口温度增加。随着流量的降低,把二次侧给水加热到饱和水和饱和蒸汽所需的热量减小,使得过冷段和两相段的长度减小,过热段长度增加。各出口参数均在250 s内达到稳定值。
5 结论
对已建立螺旋管式直流蒸汽发生器设备的数学模型进行了满功率稳态计算,结果表明本文建立的数学模型具有代表性,物理机理关系式选用合理,且求解方法正确有效。
1)对一次侧流量和二次侧给水流量进行阶跃扰动,系统的动态响应过程符合热工水力学基本规律。
2)针对螺旋管式直流蒸汽发生器的结构特点和动态特性,本文提出了基于PID调节给水流量,使得蒸汽出口压力保持恒定的控制方案。大幅度甩负荷的实验结果表明了控制方法的有效性,也验证模型的合理性。
