BP与LSTM神经网络在福建小流域水文预报中的应用对比

2020-03-11崔巍顾冉浩陈奔月王文

人民珠江 2020年2期

崔巍，顾冉浩，陈奔月，王文

(1.河海大学水文水资源与水利工程国家重点实验室，江苏南京210098； 2.福建省水文水资源勘测局闽江河口水文实验站，福建福州350001)

水文预报模型可以粗略地分成过程驱动模型和数据驱动模型两大类[1]，过程驱动模型以水文学概念为基础，模拟产流和河道演进过程，从而进行流量过程预报；数据驱动模型则基本不考虑水文过程的物理机制，通过建立输入、输出数据之间的最优数学关系，实现流量过程的预报。随着下垫面观测数据、水文气象观测数据的不断丰富，以及计算机计算能力的提升，数据驱动模型在水文预报中得到越来越广泛的关注和应用。

数据驱动模型中，人工神经网络因为具有良好的非线性映射能力，在水文领域得到了广泛应用。以Romelhart和Mcclelland[2]在1986年提出的误差反向传播算法(BP算法)为基础构建的BP神经网络是目前最常用的一种神经网络模型。由于其结构简单，并且具有良好的非线性和泛化逼近能力，以及其自组织、自适应和容错性，20世纪90年代以来就被很多研究者应用于洪水预报[3-4]及中长期径流预报[5-6]。但BP神经网络存在着网络结构难以确定、训练速度慢和预测精度低等方面的问题[7]。Elman等[8]提出的循环神经网络(RNN)可以被看作在隐含层进行了时间上的折叠，从而可以拥有无限多个隐含层，通过在隐含层的迭代计算，使新的信息被添加到每一层中，通过无限制次数的更新，循环神经网络可以将信息传递下去，使得神经网络获得对时间序列数据状态特征的记忆能力[9]。RNN在流域降雨径流预报中得到一定程度的应用，包括径流涨退过程预测[10]、降雨径流日尺度模拟[11]以及洪水预报[12]等。但Bengio等[13]发现RNN存在梯度消失问题(即梯度下降过程中，梯度随着神经网络层数的加深快速衰减，迅速接近于0，导致权重无法更新)与梯度爆炸问题(即由于初始化权重过大，误差梯度在权重更新中累积，导致网络权重大幅更新，权重出现快速增长，使得网络变得不稳定)，使得循环神经网络很难学习到长周期序列数据的状态特征。为了解决这一问题，Hochreiter和Schmidhuber[14]在一般RNN神经网络的基础上，提出了LSTM(长短期记忆)神经网络，将记忆单元添加到RNN隐藏层的神经单元中，从而使得时间序列上的记忆信息变得可以控制，能够有效解决信息的长期依赖，避免梯度消失或爆炸。近几年来LSTM神经网络成为一个非常受重视的流域降雨径流预报方法。Shi等[15]将LSTM模型运用于降雨临近预报，表明LSTM模型能够很好地捕捉时空相关性；冯钧等[16]则将LSTM模型和BP神经网络模型进行出来对比应用，并将二者结合起来形成组合预报模型，进行12 h预见期的洪水预报；Tian等[17]比较了LSTM、ERNN(Elman循环神经网络)、ESN(Echo State Network回声状态网络)、NARX(动态时间序列神经网络)和GR4J模型的日尺度径流预报结果，发现LSTM神经网络在面积较小的流域中有更好的预报精度；Kratzert等[18]将LSTM模型应用于受融雪影响的流域，说明LSTM相比于SAC-SMA+Snow-17(即萨克拉门托模型和Snow-17的组合模型)可以更好地完成日尺度上的降雨径流模拟，能够通过实测气象数据进行流量预报；Le等[19]将LSTM模型用于湄公河受上游水电站和水库泄洪影响流域的3 d预见期的洪水预报；Sahoo等[20]采用LSTM模型进行印度马哈纳迪河月尺度上的枯季流量预报，达到较高的预报精度；殷兆凯等[21]利用LSTM针对0～3 d的预见期分别建立了降雨径流模型，说明在相同预见期下，LSTM模型拥有比新安江模型更好的预报能力。

本文以福建木兰溪支流延寿溪渡里站以上流域为研究区，利用逐时实测降雨与流量数据建立BP神经网络、LSTM神经网络模型，进行未来1～24 h的逐时洪水预报，比较2种模型的预报结果，采用模块化建模方法，讨论了隐含层不同神经元数对模型训练速度和预报精度的影响以及造成精度差异的可能原因，同时探讨了如何简单有效地避免模型训练时陷入局部最优解，为将神经网络模型应用于有水文站控制的小流域短期洪水预报工作提供参考。

1 研究方法

1.1 BP神经网络模型

BP神经网络通常包含3层结构，即输入层、隐含层和输出层，见图1。BP神经网络的构建过程主要分为2个阶段：第一阶段是信号的前向传播，从输入层经过隐含层，最后到达输出层，计算出预测结果，并利用预测结果和真实值构成代价函数；第二阶段是误差的反向传播，从输出层到隐含层，最后到输入层，利用梯度下降法，依次调节隐含层到输出层的权重，输入层到隐含层的权重。在反向传播的过程中，根据误差不断调整优化各参数的值；不断重复该过程，直到收敛。

图1 BP神经网络结构示意

1.2 LSTM神经网络模型

注：×与⊙为矩阵元素积；+为相加。图2 LSTM记忆单元细节结构

1.3 模拟结果的评价指标

从整体流量过程与单次洪水预报2个角度进行模型预报精度评价。以相对误差RE、确定性系数DC作为误差指标。其中：

(1)

(2)

确定性系数DC也称Nash-Sutcliffe效率系数。其值在(-∞，1]之间，1表示预报结果完美拟合实测值。

根据GB/T 22482—2008《水文情报预报规范》对于单次洪水事件的预报结果，洪峰流量以实测洪峰流量的20%作为许可误差；峰现时间以预报根据时间至实测洪峰出现时间之间距的30%作为许可误差；径流深以实测值的20%作为许可误差，若该值大于20 mm，则取20 mm，若该值小于3 mm，则取3 mm。

当误差小于规范所规定的误差即可视为合格预报。合格预报次数与预报总次数之比的百分数为合格率，表示多次预报总体的精度水平。合格率按下式计算：

(3)

式中 QR——合格率；n——合格预报次数；m——预报总次数。

预报项目的精度按合格率或确定性系数的大小分为3个等级，见表1。

表1 洪水事件预报精度等级

2 研究流域与数据

2.1 研究区概况

实验流域为福建莆田市木兰溪支流延寿溪的渡里水文站以上集水区，流域内地形站点信息见图3，流域面积68.57 km2，属典型的亚热带季风气候，年平均降雨在2 000 mm以上。流域地处山区，地形最大高差达842 m。流域内植被覆盖良好，森林覆盖率达69.3%。流域内无水库调节，仅有少数塘坝，水体面积占0.02%。流域内有河道水文站1个(渡里)，雨量站3个(渡里、下张隆和林兜)。渡里水文站以上集水区面积小，且不受水库调节影响，能够很好展现降雨径流响应关系，且在福建省水文水资源勘测局的帮助下能够获得充足的降雨和径流逐时数据，是进行小流域降雨径流预报十分良好的研究区。

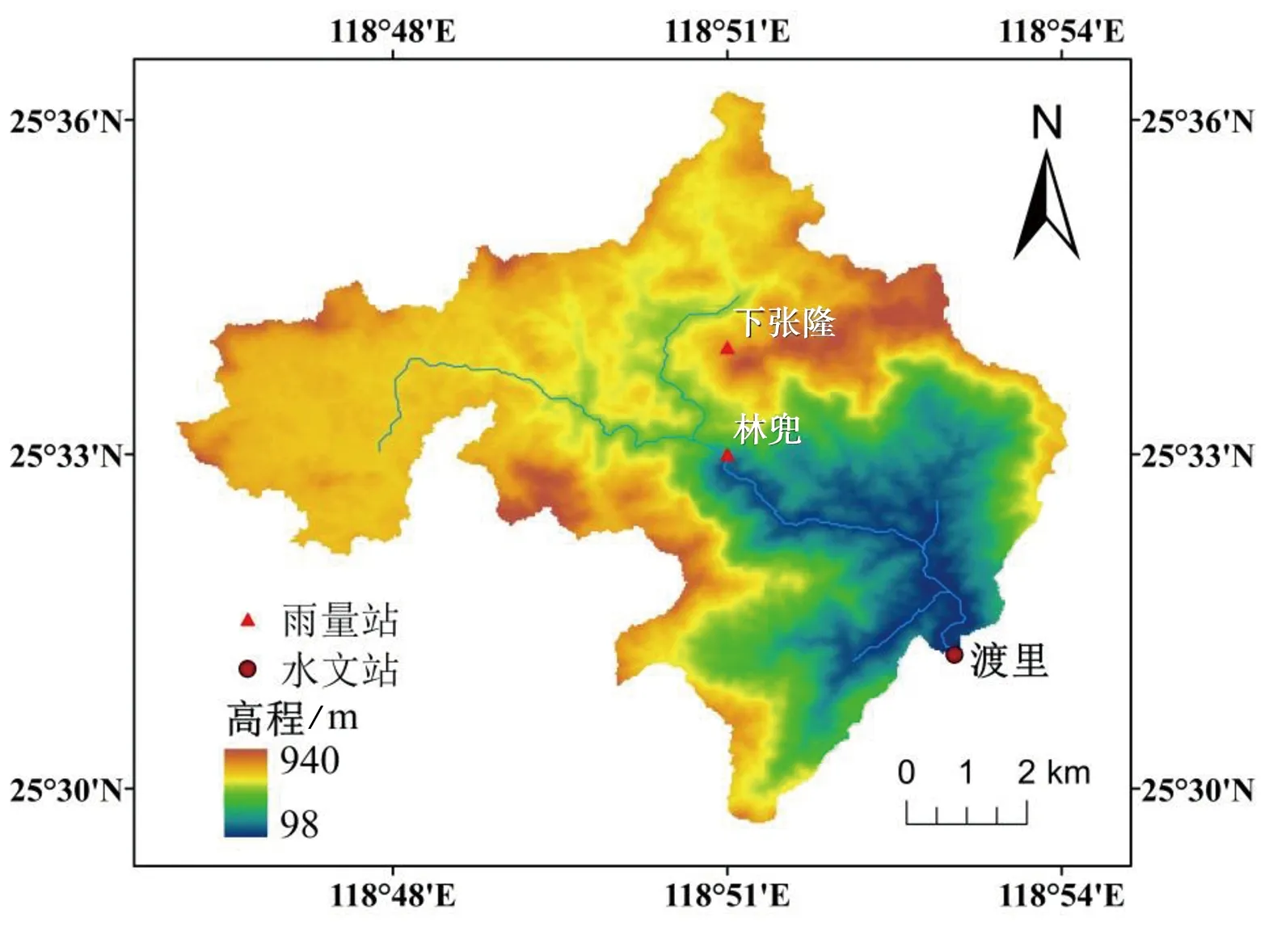
图3 延寿溪渡里站以上集水区高程及站点分布

2.2 数据

本文选用来源于福建省水文水资源勘测局水雨情数据库的渡里水文站逐时流量数据，渡里、下张隆和林兜的逐时降水数据，时间为2014年6月至2018年11月，采用泰森多边形计算流域面平均雨量后作为降雨输入。由于没有2014年6月至2018年11月的降水预报数据，所以在进行未来第2～24 h逐时预报时用同期上一时刻的实测降雨数据代替降水预报数据。

利用MODIS 16 d尺度的植被指数(NDVI)数据(MODIS13A2)，计算流域平均每16 d的多年平均植被指数，并采用三次样条法插值成逐日数据，作为神经网络反映流域内植被的季节变化的一项输入。

3 模型构建与结果分析

3.1 神经网络预报模型构建

神经网络虽然已经在水文预报中得到了较为广泛的应用，但是对建模环节中的一些问题仍然没有系统性的解决方案，这些问题包括如何确定网络结构(包括确定输入节点，如何确定隐含层层数以及神经元数)，如何确定训练的迭代次数以及避免训练过程中陷入局部最优解，以及如何考虑降雨径流过程不同阶段的动态特征差异等。

3.1.1模型结构的确定

a) 输入节点。为便于比较，BP与LSTM模型将在输入节点上将保持一致，采用同样的输入及预处理方法。2个神经网络的降雨数据输入节点通过计算当前流量与前期累积降雨的相关关系来确定。计算了1～6 h的逐小时降雨，6～12、12～18、18～24、24～30、30～36 h的6 h累计降雨，36～48、48～60、60～72 h的12 h累积降雨，结果见图4。由图4可见，1～6 h逐小时降雨,6～12、12～18、18～24 h的6 h累积降雨量与当前流量具有较高的相关性，相关系数都超过0.35，因此选取这9项累积降水数据作为降雨输入。2个神经网络的流量数据输入节点数通过对流量数据进行了自相关(AR)和偏自相关(PAR)(图5)分析确定。由图5可见，流量具有很强的自相关特征(图5a)，即使30 h前的流量值与当前流量也具有较高的相关性，但是根据流量的偏自相关图(图5b)，5 h之后的流量值与当前流量的相关系数小于0.2。因此，可以考虑将前1～5 h的流量值作为模型的输入数据。但在进一步通过多次模型训练尝试后，确定流量数据满足要求的最佳滞时为2，即将前1 h和前2 h流量值作为模型的输入。除了上述的降水及流量数据输入，考虑到植被截留过程会减少到达地面的有效降雨量，而流域内植被具有季节性变化，植被的年内生长变化对径流量有着较大影响。所以将NDVI数据也作为神经网络的一项输入。

图4 流量与前期不同时段累积降雨量的相关关系

a) 自相关

b) 偏自相关图5 逐时流量数据的自相关和偏自相关分析

b) 输入数据预处理。由于流量数据的数值尺度和单位与降雨量数据存在差异，以及激励函数本身的特性，如sigmoid函数对于小于-5、大于5的输入数据响应值不敏感，趋于0和1。所以在构建神经网络模型时，必须对流量和降雨数据进行归一化处理，使每个输入、输出节点的数据均值近似为0，方差为1。同时，为了缩小数据中极大值造成的影响，放大极小值的影响，在进行归一化处理前先对数据取对数。为了避免数据中的0值影响对数计算，取0.01代替数据中的0值。经过归一化处理后，数据的绝对值将变成一种相对关系，来消除量纲对模型运算的干扰[21]，同时可加快梯度下降的收敛速度。

c) 隐含层层数及隐含节点数。神经网络的建立过程中，隐含层层数和神经元数会对结构和训练产生多方面的影响。增加神经网络隐含层层数可以提高学习精度，Hornik等[22]证明一个拥有足够多的神经元的单隐含层神经网络就能够完成从输入数据到输出数据之间任何可测量的函数关系，并达到期望的精度。但是同时让模型结构变得更加复杂，也让训练时间大大增长。Villiers和Barnard[23]的研究表明，由2个隐含层组成的神经网络的鲁棒性较差，收敛精度也较低。所以在设计神经网络时应优先考虑有1个隐含层的3层网络。因此本文中BP和LSTM模型的隐含层层数都设定为1个。

对于隐含层内神经元数量，本文采用“试错法”，通过比较不同神经元数量对验证数据预报结果的影响，来确定合适的神经元数量。图6为在不同神经元数下，以确定性系数DC(Nash效率系数)作为评价指标，BP模型与LSTM模型对未来1～24 h流量滚动预报精度的变化。

从图6a、6b可以看出，BP模型的精度在n=10(图6a黑线)时达到最高，Nash效率系数为0.987～0.711，当神经元数量继续增加时，Nash效率系数会随着神经元数量的增加而降低，同时训练时间大大增长。所以BP模型最终神经元数量确定为10个。LSTM模型的精度随着神经元数量的增加而提高，当n=64(图6b黑线)时，未来1～24 h的滚动预报Nash效率系数最高，为0.969～0.747，当n>64后，Nash效率系数则出现了下降，同时训练时间大大增长。所以LSTM模型最终神经元数量确定为64个。

从上述对比可见，BP神经网络的最优隐含层节点数明显小于LSTM的最优节点数据，其原因在于：不论是BP网络还是LSTM网络，过于复杂的神经网络都可能带来模型的过拟合问题，但这个过拟合问题对于BP网络非常突出，而对于LSTM网络，其本身的记忆与遗忘功能使得权重在更新时，不仅充分利用了当前时刻的数据特征，还利用了门的结构来记住还是遗忘前一时刻的数据特征，也就使得并非所有数据都对权重的更新产生影响，能够一定程度上降低过拟合产生的可能，因而LSTM网络的最优隐含层神经元数大大多于BP网络。

a) BP模型

b) LSTM模型图6 不同模型的神经元数对验证数据预报精度的影响

3.1.2模型训练

使用2014年6月至2016年6月的逐时流量数据、逐时降雨数据和NDVI数据，共3类分12个节点输入模型，对模型进行训练。

考虑到流域的降雨-径流关系在不同的降雨量级以及不同的流量涨落阶段可能具有一定的差异性，建立一个单一的全局模型无法让模型很好地学习到不同阶段流量涨落变化和降雨量的关系，因此本文在神经网络建模中使用模块化方法[24]，首先按照阈值将降雨和流量数据划分若干组，然后对每组数据分别训练不同的模型。本文将降雨流量数据分成4组进行训练：第一组为降雨大于1 mm且流量大于5 m3/s；第二组为降雨小于1 mm，流量大于5 m3/s；第三组为降雨大于1 mm，流量小于5 m3/s；第四组为降雨小于1 mm且流量小于5 m3/s。

模型训练前，还需要确定包括模型的损失函数、学习率、批处理量参数(batch-size)、训练集中的交叉检验数据比例(validation-split)和训练最大迭代次数等。

本文中2种模型的损失函数均选择均方误差(MSE)，计算公式如下：

(4)

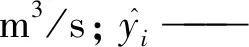
学习率决定了模型权重更新的幅度，如果学习率很低，训练会变得可靠，但是需要花费更多的优化时间；如果学习率很高，输出误差对权重的影响就越大，权重更新就越快，但可能无法收敛。但是最佳学习率的确定仍旧缺少最优的方法。本文中BP和LSTM模型的学习率依赖经验分别定为0.20、0.01。

批处理量参数(batch-size)指模型训练中梯度下降时每个批次所含的样本数。该参数的大小影响模型的优化程度和速度。如果不设置该参数，意味着模型在计算时，是一次把所有的数据输入模型中，然后进行梯度下降算法，由于在计算梯度时使用了所有数据，计算速度慢，需要更多的迭代次数来达到最优。而本文由于使用多年逐时数据进行建模，数据量较大，一次性把所有数据输入模型，内存占用率高，会极大加重模型计算负担，影响训练速度和模型精度。所以经过试错，2个模型的批处理量参数(batch-size)均设置为240。

训练集中的交叉检验数据比例(validation-split)是指从数据集中切分出一部分作为验证集，验证集不参与训练，并且在每次迭代时在验证集中评估模型的性能，如计算损失函数。本文中2个模型的该参数设置为0.2。

为了确定2种模型的单次训练的最大迭代次数，在上述参数设定的条件下，分别将BP和LSTM模型训练一次，绘制2种模型的损失函数变化，见图7。BP模型在迭代500次后损失函数的数值仍然高于LSTM模型100次迭代后损失函数的数值。所以为了避免训练时间浪费的同时达到最佳训练效果，确定BP模型最大迭代次数1 000次，LSTM模型迭代次数100次。

a) BP模型

b) LSTM模型图7 不同模型损失函数随迭代次数的变化

神经网络的训练过程对初始权重较为敏感。由于初始权重的不同，每次训练都可能会得到一组不同的参数。为了获得最优参数，一种方法是采用多组独立初始权重值分别进行训练，然后从多组训练结果中选择神经网络模型[25]，但这种最优网络仅是对训练数据最优，对未来未知的真实验证数据未必最优。也就是说训练中最佳的神经网络模型对于未来的数据并不一定能达到最优的预测结果。Wang等[26]提出了一种简单有效的解决局部最优的方法，即将一个模型训练若干次(如20次)，得到20组模型参数，选择其中较好的10组，形成一组模型集合，并将这个模型集合的结果取平均值作为最终的输出。本文采用了这种方法。

3.2 模型验证

利用训练好的模型做下一个小时(T+1)的流量预报，再以预报的T+1 h流量作为当前流量输入，预报T+2 h流量，以此循环滚动，从而完成未来T+24 h的循环滚动预报。本文选择2016年7月至2018年11月的预报结果，验证模型预报精度。

a) 对整体流量过程的预报精度评价。BP与LSTM模型验证期的24 h滚动预报结果的Nash效率系数见图8。2个模型不同预见期的验证期预报结果散点见图9。由图8可以看出，2种模型在第1 h的预报，Nash效率系数大于0.96(BP模型为0.975，LSTM模型0.968)；随着预见期的延长逐渐下降，但LSTM模型整体预报效果优于BP模型，并且预报精度的衰减速度大大慢于BP模型。LSTM模型滚动预报至第24 h的Nash效率系数仍达到0.74，达到乙级预报精度，而BP模型则降到0.51，符合丙级预报精度。由此可见，在整体流量过程预报值中，综合而言，LSTM模型精度显著优于BP模型。

图8 BP、LSTM模型滚动预报结果Nash效率系数

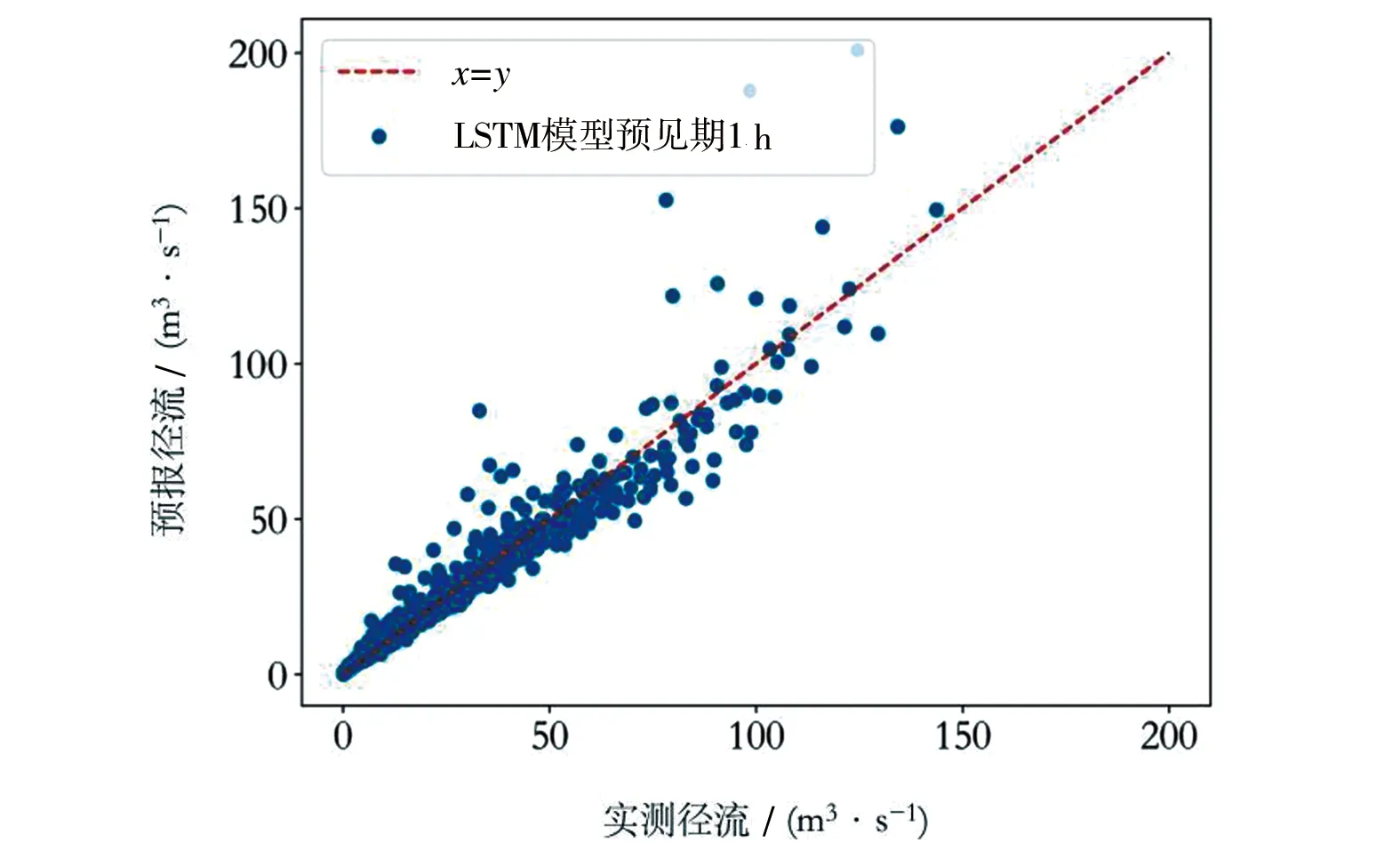
a) LSTM模型1 h预见期

b) LSTM模型6 h预见期图9 LSTM、BP模型不同预见期预报结果散点

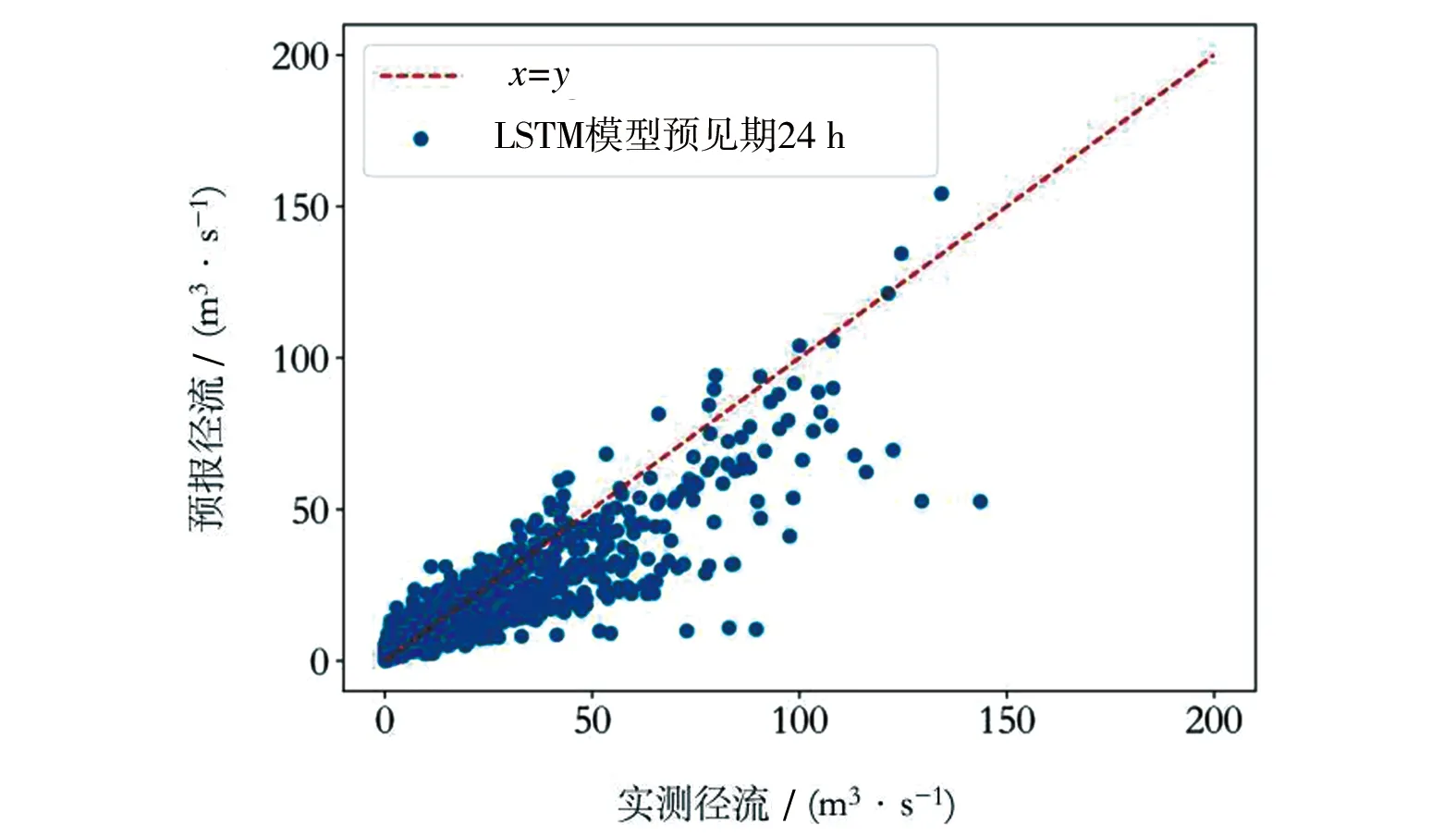
c) LSTM模型24 h预见期

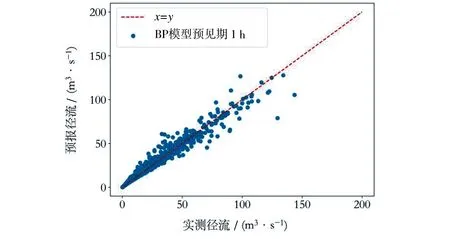
d) BP模型1 h预见期

e) BP模型6 h预见期

f) BP模型24 h预见期续图9 LSTM、BP模型不同预见期预报结果散点

b) 对洪水事件的预报精度评价。挑选2016年7月后的15场洪水作为验证集，将洪水事件期间的24 h滚动预报值分别与实测数据相比较，对2个模型对洪水事件中的预报精度进行了进一步验证。根据GB/T 22482—2008《水文情报预报规范》，将15场洪水24 h内不同预见期内洪峰流量、峰现时间和径流深3个评价指标的合格率绘制成折线，见图10。其中，图10a为洪峰流量误差合格率，图10b为峰现时间误差合格率，图10c为径流深误差合格率，图10d为综合3个误差指标后模型的最终合格率，即当一场洪水3个指标都合格时，该场次洪水的预报即为一场合格洪水。LSTM模型3个指标的合格率以及综合合格率都优于BP模型。其中LSTM模型洪水预报在预见期为24 h的预报合格率为60%，达到丙级预报精度，而BP模型为20%，未达到丙级项目精度等级。

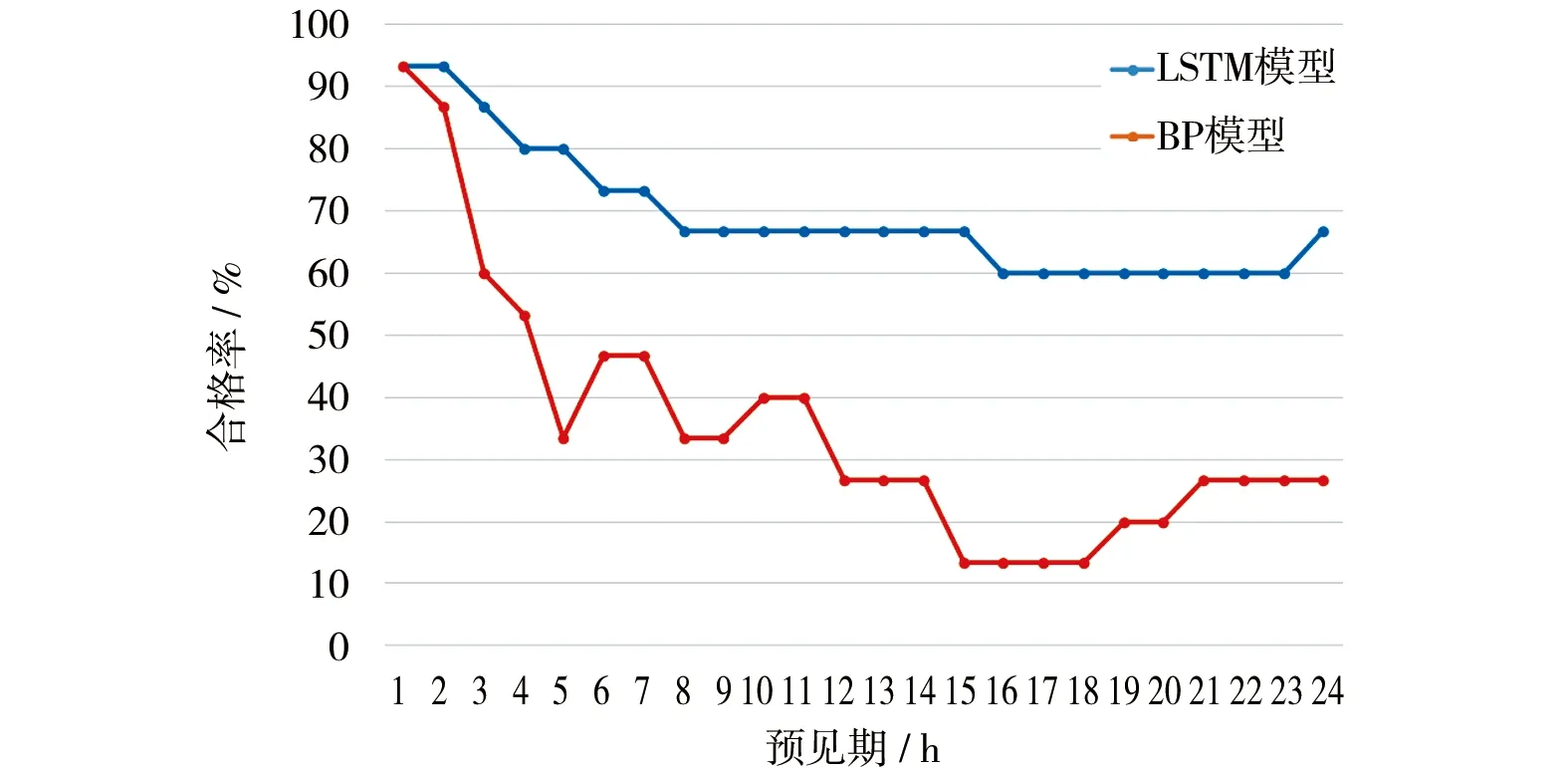
a) 洪峰流量误差合格率

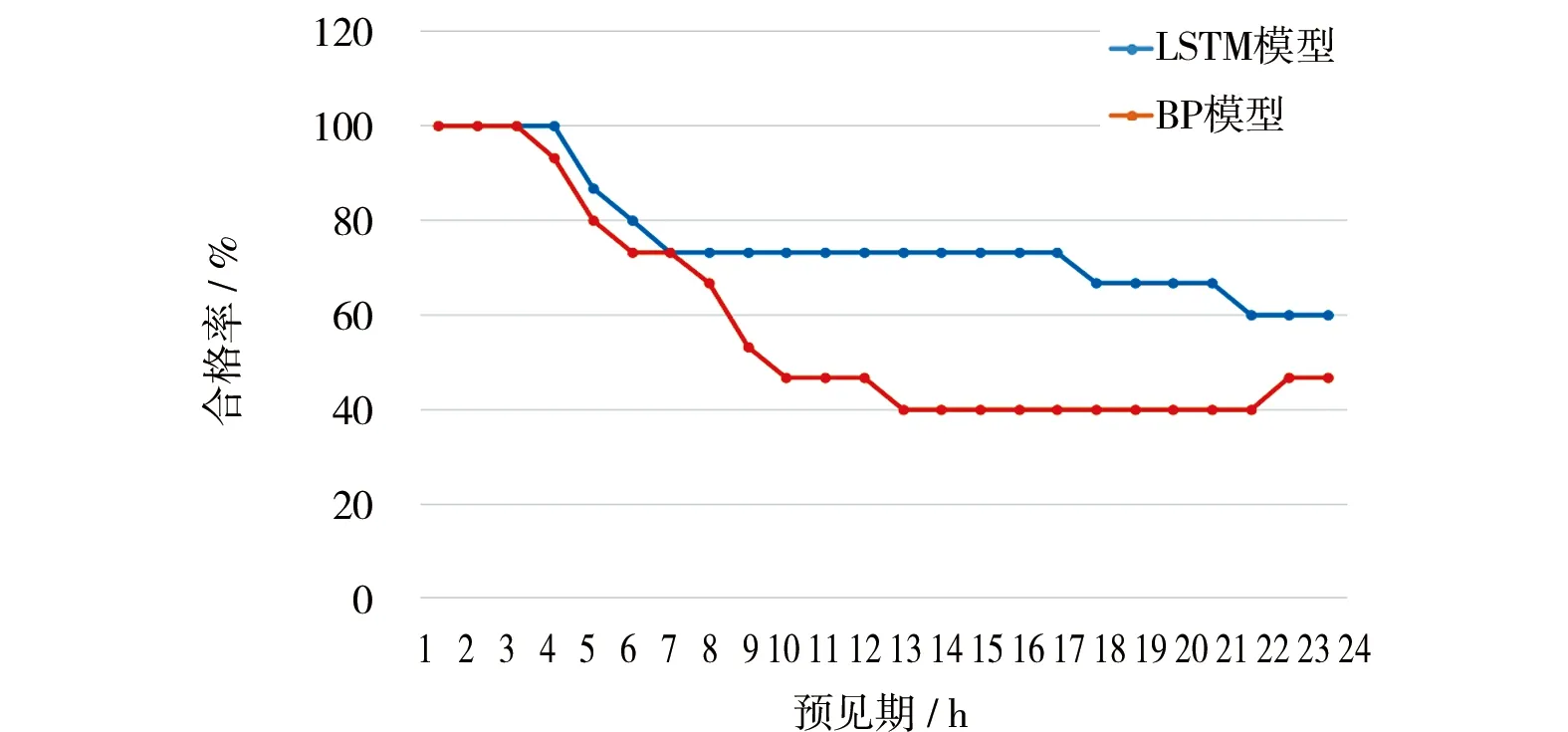
c) 径流深误差合格率

d) 模型最终合格率续图10 评价指标合格率折线

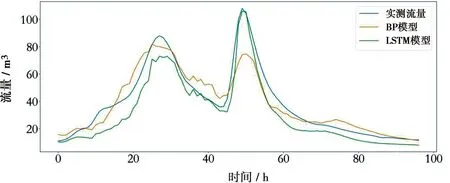
进一步以20160927和20180828 2场洪水为例，比较了BP模型与LSTM模型对洪水过程预报的能力。20160927场次洪水过程线见图11，图11a、11b、11c、11d预见期分别为1、6、12、24 h。在24 h的预见期内，LSTM和BP模型都可以较好反映洪水涨落过程。在预见期为1 h时，2个模型预报能力相当。随着预见期的延长，BP模型出现了系统性地偏大，高估了整个洪水过程的洪量。20180828场次洪水过程线见图12，图12a、12b、12c、12d分别代表预见期为1、6、12、24 h。20180828场次洪水拥有2次涨水过程。在24 h的预见期内，2种模型都能够反映出2次涨水退水过程。但是BP模型却在2个洪峰处出现了严重的低估现象。在预见期6～24 h的预报结果中BP模型在第一个洪峰处的预报值高于了第二个洪峰的预报值，与实测数据不符，洪峰预报能力退化明显。通过对2场洪水事件预报能力的对比，LSTM模型在预测洪峰流量以及洪水过程上拥有更好的性能，能够很好地预报出洪水的涨退水过程以及洪量。

a) 预见期1 h

b) 预见期6 h

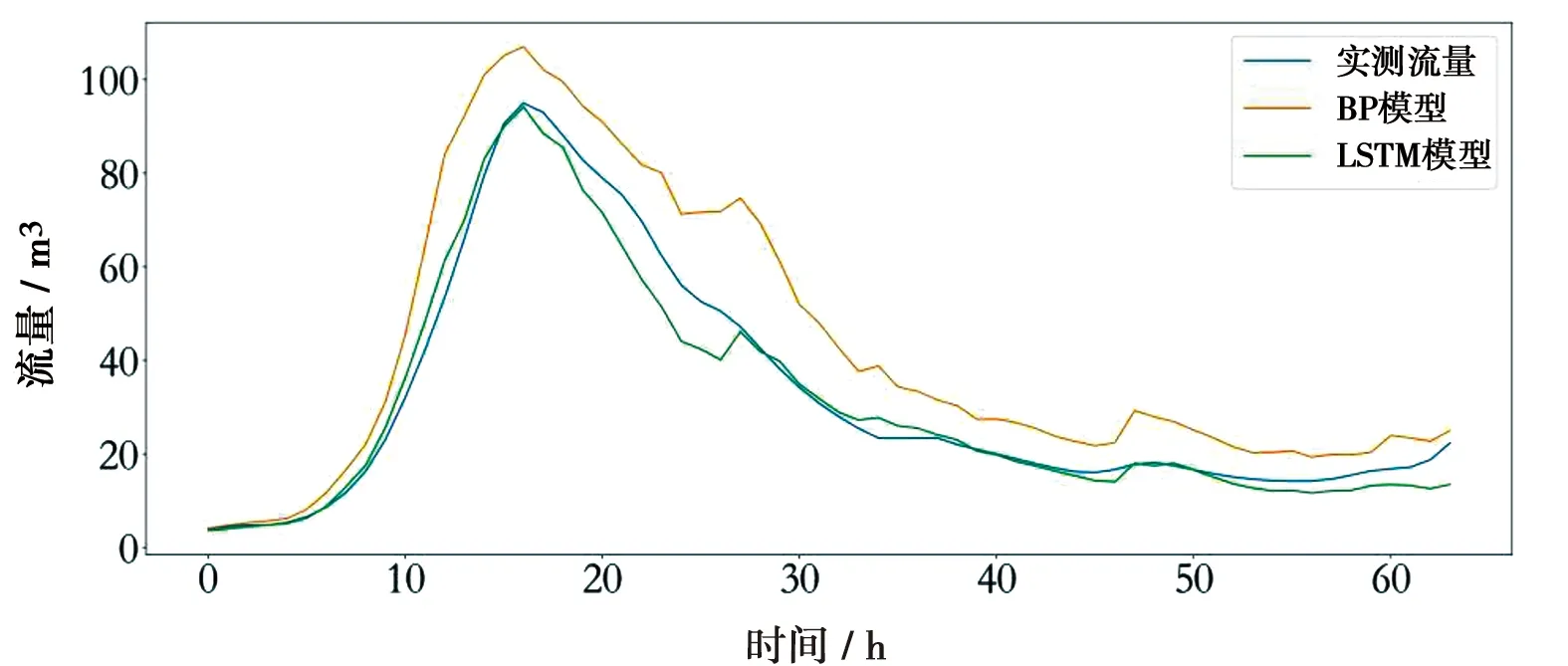
c) 预见期12 h

d) 预见期24 h图11 预见期不同时20160927场次洪水预报效果比较

a) 预见期1 h图12 预见期不同时20180828场次洪水预报效果比较

b) 预见期6 h

c) 预见期12 h

d) 预见期24 h续图12 预见期不同时20180828场次洪水预报效果比较

4 讨论

BP神经网络与LSTM神经网络模型都属于黑箱模型，从本文应用结果来看，LSTM模型比BP神经网络具有更好的逐时流量预报精度，其主要原因在于流域降雨径流过程中的土壤水蓄量、地下水蓄量等状态变量对河流流量具有巨大的影响，也就是说状态信息对于预报精度的可靠性具有很大作用。LSTM神经网络利用由遗忘门、输入门和输出门组成的记忆单元，来控制丢弃或增加信息，使得信息可以有选择地通过，从而实现对时间序列过程状态特征的记忆功能，而BP神经网络缺乏这种对状态信息的处理功能。

由于LSTM的记忆与遗忘功能使得累积误差减少，这使得LSTM模型精度衰减速度远远小于BP模型，在循环滚动预报中，随预见期的延长,精度的优势不断突显。同时在本文应用中LSTM模型的隐含层神经元经过试错确定为64个，BP模型设定为10个。在这种设置下，LSTM网络在100次迭代次数下已经能够使得损失函数达到最优，而BP需要近1 000次迭代才能带到LSTM模型100次迭代的结果。如果将2个模型的隐含层神经元数都设定为64个，LSTM网络的训练速度将更明显优于BP模型。

尽管LSTM网络中的“门”结构使神经元之间能相互作用，可以使损失函数更好地收敛，使得LSTM趋近全局最优解的能力，LSTM模型仍然无法完全避免出现局部最优解的可能性。为此本文使用了Wang等[26]提出的解决方案，即训练多次模型，计算结果后取平均的处理方式。该方法简单易行，也确实在一定程度上避免了局部最优解对模型精度的影响。此外，还可以尝试其他一些解决方案，比如使用变化的学习率或者蜂-蚁群算法等[27]方法，以期进一步提高预报模型的稳定性。