利用非合作航天器双特征结构的相对姿态确定方法*
2020-03-11王大轶邹元杰史纪鑫黄美丽
王大轶,鄂 薇,邹元杰,史纪鑫,黄美丽
(北京空间飞行器总体设计部·北京·100094)
0 引 言
空间非合作目标具有无标识、无应答、外形尺寸未知的特点,对其进行相对姿态测量具有较大的难度。光学相机所获取的图像包含非合作目标外形、轮廓、色彩、纹理等详细信息,利用视觉图像处理算法能够将这些信息转换为目标的运动参数,因此广泛应用于近场非合作目标的运动测量任务中[1-3]。基于图像信息的航天器相对姿态确定方法主要分为基于CAD模型与基于特征两类,基于CAD模型的相对定姿方法通过最小化航天器图像与CAD模型在图像平面投影的误差实现定姿,而基于特征的相对姿态确定方法利用航天器结构特征与图像特征之间的关系实现定姿。对于不具备CAD模型先验知识的非合作航天器,基于特征的方法能够有效解决非合作航天器的相对姿态确定问题,因为即便是非合作航天器自身也会存在对接环、太阳帆板、推进器以及支架等典型结构,这些结构能够提供相对定姿所需的图像特征。
相对姿态确定中常用的图像特征主要为点、线、圆特征。点特征可依靠人工标识点直接获取,也可利用特征点检测算子根据图像的纹理与灰度获取。由于非合作目标不具有人工标识点,通常利用特征点检测算子提取特征点,目前性能较优且广泛应用的算子包括SIFT[4]、SURF[5]以及ORB[6]等,但是航天器空间光照条件变化较大,且表面一般覆盖高反射系数的隔热材料,在轨道周期内不能持续将相同的特征点提取出,从而影响图像序列间的特征匹配与姿态估计。Yilmaz等[7]详细对比分析了目标跟踪任务中不同特征的性能,研究表明目标的边缘特征相对于色彩、纹理与光流等特征受光照的影响较小,以边缘检测算法为基础的线特征与圆特征更适用于非合作目标的相对定姿。航天器的星体、太阳帆板以及支架等结构能够提供丰富的直线特征,在边缘检测中这些结构的轮廓线都能够充分保留下来,直线特征通常利用Hough变换进行检测,检测出的直线集合可以根据分布特征进一步进行多边形检测。星箭对接环作为航天器上普遍存在的结构能够提供圆特征,Luckett等[8]分别利用点、线、圆特征进行相对定姿,并分析了利用三种特征的测量精度,实验表明基于圆特征的相对定姿精度最高且跟踪效果也更加鲁棒,也正因为这样,许多研究者都利用能够提供圆特征的星箭对接环结构进行定姿。Shiu和Ahmad[9]与Safaeerad等[10]详细推导了利用单个圆求解平面法向量的过程,证明了单圆定姿具有二值性。为了去除单圆定姿的虚假解,翟坤[11]采用激光雷达的测距信息来去除二值性,苗锡奎[12]则采用圆外一已知距离的点作为补充信息去除二值性,张铁毅[13]在已知星箭对接环半径的情况下计算姿态信息。吴斌等[14]、陈至坤等[15]以及Du等[16]都利用星箭对接环与其所在卫星本体的直线特征共同定姿,根据矩形面上平行线计算消失点来去除二值性。鄂薇等[17]基于投影同心圆代数约束的定姿原理,利用星箭对接环的双环结构实现了不依靠额外信息的相对姿态确定。但是仅利用星箭对接环结构只能够得到对接环所在平面的法向量,没有获取目标航天器全部的姿态信息,而仅利用太阳帆板结构只能在帆板为固定翼时等效为本体姿态。
针对以上问题,本文提出了一种利用航天器双特征结构的相对姿态确定方法来获取非合作目标的完整姿态。该方法利用目标航天器的星箭对接环结构与太阳帆板结构联合定姿,其中星箭对接环提供同心圆特征,并且基于投影同心圆代数约束求解星箭对接环所在平面法向量;太阳帆板提供矩形特征,并且基于平行线消失点原理求解太阳帆板的旋转轴方向向量。从而可以利用这两个方向向量确定出完整的相对姿态,并且能够在考虑旋转翼的情况下实现对非合作航天器获取完整的相对姿态参数。
1 坐标系定义与姿态描述
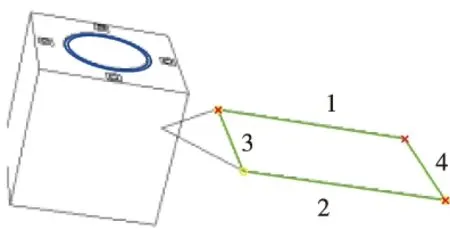
首先建立描述目标航天器相对姿态的坐标系,本文所研究的对象为传统航天器,星体为箱型结构,并且包含太阳帆板与星箭对接环结构,本文设定星箭对接环与太阳帆板分别位于航天器本体的相邻面,如图1所示。当太阳帆板以其他模式安装在星体上时,坐标系可以进行相应的修改,但并不影响本文定姿算法的应用。
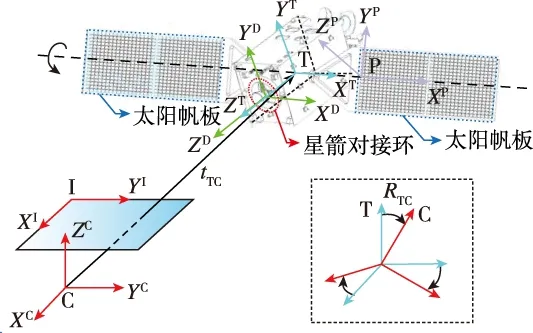
图1 目标航天器相对姿态描述所涉及的坐标系Fig.1 The frames involved in relative attitude description of target spacecraft
利用双特征结构进行相对定姿所用坐标系包括跟踪航天器相机坐标系C、图像坐标系I、目标航天器本体坐标系T、目标航天器星箭对接环坐标系D以及目标航天器太阳帆板坐标系P。设跟踪航天器的相机固连在本体上,C系的Z轴为相机光轴方向,C系的XY轴与I系的XY轴相平行。T系原点建立在星体质心上,Z轴垂直于星箭对接环所在平面,X轴平行于太阳帆板转轴。D系建立在星箭对接环上,原点位于星箭对接环中心,Z轴垂直于星箭对接环所在平面并与T系Z轴相平行。P系建立在太阳帆板上,当太阳帆板为旋转翼时,P系相对于T系是一个动坐标系,但旋转轴方向不发生改变,因此令P系X轴沿帆板旋转轴方向,该轴与T系X轴方向相平行。
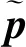
(1)
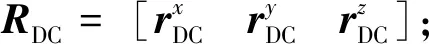
P系中的任意点在相同时刻通过摄像机投影到图像平面的转换关系为
(2)
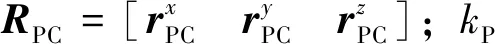
设RTC为T系到C系的旋转矩阵,RTC可表示为
(3)
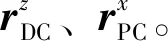
RTC=
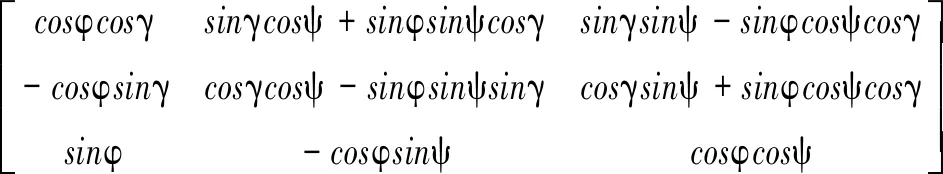
(4)
姿态角可以由姿态矩阵RTC计算出,表示为
(5)
式中Rij为RTC第i行第j列的元素。
2 双特征结构的图像提取方法
利用航天器特征结构进行相对姿态确定,首先对航天器图像进行Canny边缘检测,进而在边缘图像中提取星箭对接环的圆特征与太阳帆板的四边形特征。
2.1 星箭对接环图像提取方法
采用Fornaciari[18]等提出的快速椭圆检测方法,该方法在获得相似甚至更好性能的前提下,其检测性能较其他方法[19-23]快得多。任意边缘点pi的图像坐标可以表示为(xi,yi),以及梯度相位值θi。首先利用θi可以将边缘点分为两类,表示为
D(pi)=sign(tan(θi))
(6)
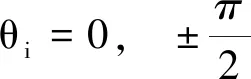
(7)
每段圆弧上都包含三个特殊点,圆弧段的左端点pl、右端点pr与中点pm。将圆弧用一个矩形包围盒围住,pl、pm分别为包围盒两个不相邻的顶点,圆弧可以将包围盒分为左右两个区域,定义当左侧面积大于右侧时,该段圆弧为凸圆弧,当右侧面积大于左侧时,该段圆弧为凹圆弧,当两侧面积相等时将该圆弧舍去。因此,第k段圆弧的凸凹性可以表示为
(8)
基于每段圆弧的D(pi)与C(αk)值,可以按照相位区间将αk分为四类,由于αk中的每个边缘点D(pi)相同,因此D(pi)等价于D(αk),αk所对应的相位区间可表示为
(9)
(10)
凸凹性约束表示为
(11)
(12)
相对位置约束表示为
(13)
(14)
(15)
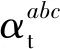
2.2 太阳帆板的图像提取方法
太阳帆板在图像上能够提供四边形特性,利用两组平行线之间的消失点可以求解太阳帆板的相对姿态。由于受到测量距离以及光照变化的影响,帆板的边缘直线通过Hough变换检测后会出现重叠、分段等现象,如图2所示。
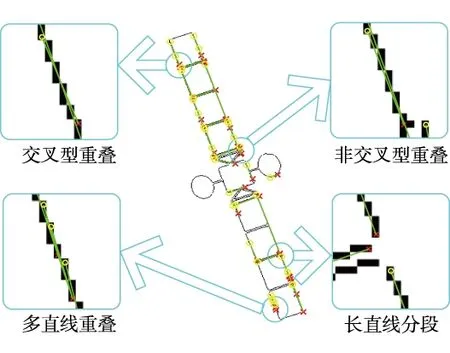
图2 航天器边缘图像的Hough直线检测结果Fig.2 Hough line detection results on satellite edge image
为了解决直线边缘重叠、分段的现象,对Hough检测后的直线集进行融合,将属于相同直线边缘的线段合并为一条直线。设Hough检测后的直线集合中任意两条线段l1与l2的极坐标形式为
l1:ρ1=ucosθ1+vsinθ1
l2:ρ2=ucosθ2+vsinθ2
(16)
当|θ1-θ2|<θth且|ρ1-ρ2|<ρth时,判定l1与l2可以进行融合,融合后的l3可写为
l3:ρ3=ucosθ3+vsinθ3
(17)
设p11、p12分别为l1两个端点的图像坐标,p21、p22分别为l2两个端点的图像坐标,利用(18)求出任意两个端点之间距离的最大值Lmax所对应的端点,并将这两个端点作为融合后l3的端点。
(18)
设融合后的直线集为{li},i=1,…,n,在{li}中检测凸四边形主要是将直线集分组,首先在{li}中检测相邻的直线,设任意两条直线li、lj利用(19)计算这两条直线端点之间的最小距离Lmin,
(19)
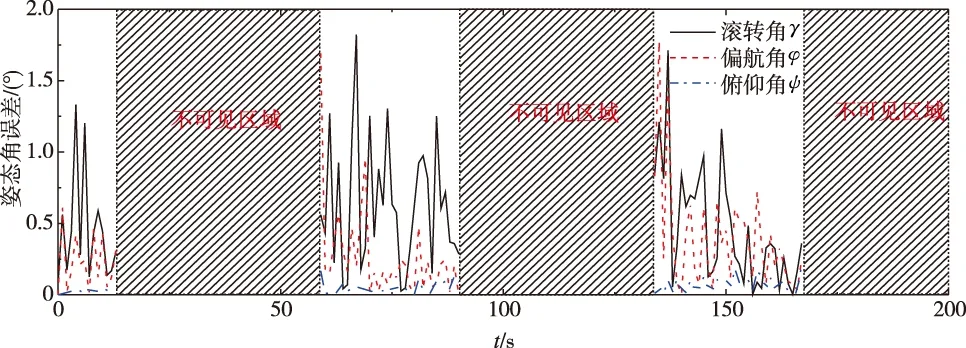
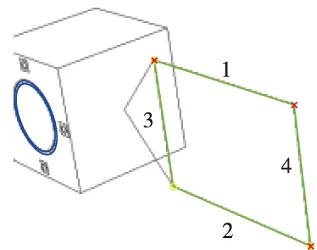
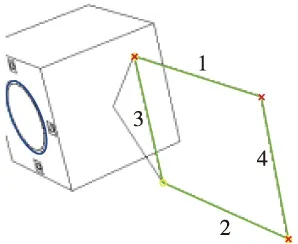
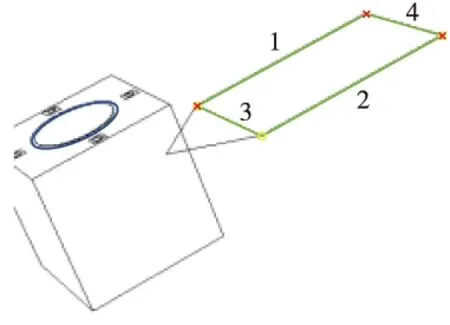
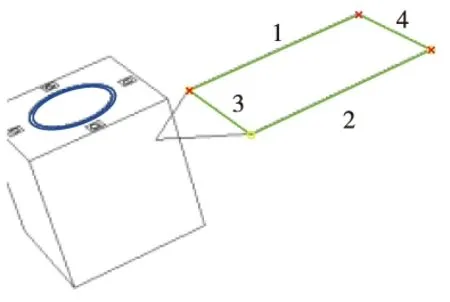
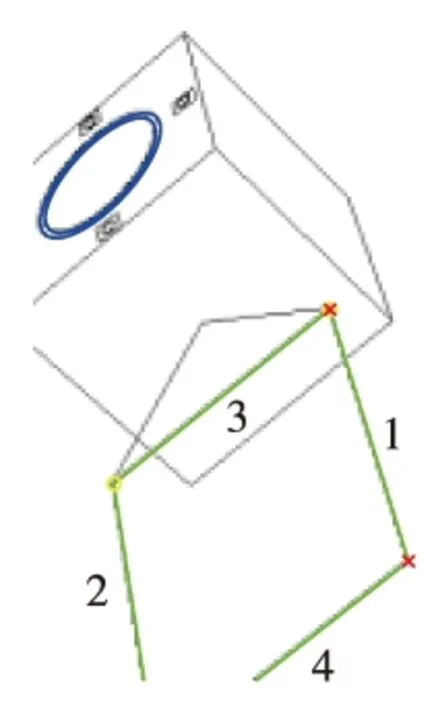
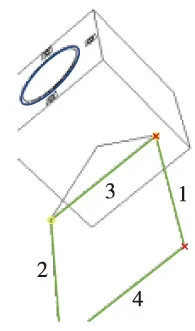
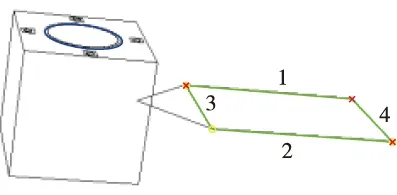
当Lmin 然后在{(li,lj)}中搜索共用一条相邻边的直线组,设两组存在公共直线的直线对为(li,lj)与(li,lk),其中li为公共直线。首先判定lj、lk是否相邻,当lj、lk也相邻时,lj、lk可能连接在li的同一端点,或li、lj、lk构成一个闭合的三角形,这两种情况都说明li、lj、lk不能构成凸四边形;当lj、lk不相邻时,将lj、lk与li不相邻的两个端点相连,计算这个四边形的内角和,当内角和为360°时,判断li、lj、lk属于一个凸四边形的三线组,遍历所相邻直线对集合可以得到凸四边形三线组集合{(li,lj,lk)}。 最后,在{(li,lj,lk)}中搜索具有两条相同直线的三线组,当具有以下四种情况时认为两个三线组可以构成一个凸四边形,分别为{(li,lj,lk), (lm,lj,lk)},{(li,lj,lk), (lk,li,lm)},{(li,lj,lk), (lj,li,lm)},此时li、lj、lk为一个凸四边形,其中li、lm与lj、lk为凸四边形的两组对边。 至此利用以上方法可以检测出图像中凸四边形集合,但是并不是所有的凸四边形都是由矩形的太阳帆板投影形成的,在3.2节中将利用平行线消失点原理去除非矩形投影的凸四边形。 (20) (21) 设星箭对接环的同心圆环半径分别为ρ1、ρ2,圆心位于D系坐标原点,该对同心圆环J1、J2的二次型可写成如下形式 (22) (23) 归一化焦平面上的圆锥曲线方程可以表示为 k1u′2+k2v′2+k3u′v′+k4u′+k5v′+1=0 (24) 将式(23)代入到式(24)中,可得 (25) (26) 式中:ξ1、ξ2为非零实数。 (27) (28) (29) (30) 式中:(xIvi,yIvi)为pIv1的图像坐标,i=1,2;(x1Cvi,y1Cvi,1)为pIv1摄像机焦距归一化成像平面的成像点坐标,i=1,2。 (31) P系的Y轴在摄像机坐标系可表示为 (32) P系的Z轴在摄像机坐标系可表示为 (33) 图4给出了跟踪观测过程中利用双特征结构进行定姿的姿态角度误差。在跟踪观测过程中累计111s能够在图像中同时检测出星箭对接环与太阳帆板结构,占总仿真时间的55%。在可见弧段内滚转角γ的最大误差为1.8212°,平均误差0.5251°;偏航角φ的最大误差为1.7784°,平均误差0.3143°;俯仰角ψ的最大误差为0.0533°,平均误差0.2158°。从图中可以看出,当目标运动到不可见区域时姿态角误差急剧增大,此时为特征在图像中能够识别出的极限角度。 图5分别给出了目标航天器进入到不可见区域时刻与前一时刻的图像提取结果。在t=14、61、91、136s时,目标航天器的双特征结构能够从图像中检测出,而t=15、60、92、135s时,目标航天器的星箭对接环结构只能等效识别出一个单环,此时不能够进行姿态确定。相对于星箭对接环结构,太阳帆板能够识别出的姿态范围更大,并且直线提取的计算量相对于椭圆提取更小。当太阳帆板不与本体产生相对运动时,直线型结构的帆板是一种更适用于定姿的自然特征,可仅利用单一帆板结构直接确定出完整三个姿态角。 图4 跟踪过程中相对姿态角度误差Fig.4 Relative attitude angle error in tracking process (a) t=14s (b) t=15s (c) t=60s (d) t=61s (e) t=91s (f) t=92s (g) t=135s (h) t=136s 本文研究利用特征结构的非合作航天器相对姿态确定方法,提出了一种利用星箭对接环与太阳帆板双特征的联合定姿方法。分别对星箭对接环与太阳帆板结构的图像提取算法进行研究,利用快速椭圆检测算法提取星箭对接环的同心圆环结构,并在Hough直线检测的基础上实现了太阳帆板四边形提取。进而基于投影同心圆代数约束求解星箭对接环所在平面法向量,基于平行线消失点原理计算太阳帆板旋转轴方向向量,能够在太阳帆板为旋转翼的条件下,实现利用双特征结构求解完备的相对姿态角。为验证利用双特征的相对姿态确定方法有效性,仿真生成包含星箭对接环与太阳帆板的失效翻滚航天器图像,通过对仿真图像进行特征提取与姿态确定计算,验证了该方法能够有效确定目标的相对姿态。但是由于失效航天器处于翻滚状态,相对姿态只能在特征可见条件下进行计算,并且在可见极限角附近的误差较大,仿真实验表明最大姿态角误差在2°以下,在可见条件较好的情况下相对姿态角误差较小。3 相对姿态确定方法
3.1 基于投影同心圆代数约束的定姿原理
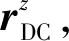
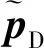
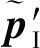
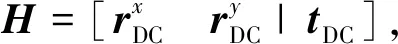
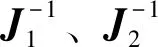
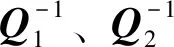
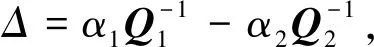
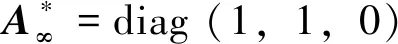

3.2 基于平行线消失点定姿原理
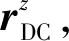
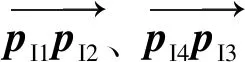
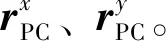
4 失效翻滚航天器相对姿态确定仿真实验

5 结 论
