基于组合线阵的近程运动小目标被动定位跟踪
2020-03-10许高凤安妍妍杨丰茂靳仕源
许高凤 安妍妍 杨丰茂 张 乔 靳仕源
(中电科海洋信息技术研究院有限公司 北京 100041)
0 引言
针对水下小目标的浅海入侵、港口渗透侦察等威胁,近岸水域水下安全防御措施需不断加强完善,蛙人探测声呐系统是一种有效的探测手段。与主动蛙人探测声呐相比,被动探测阵具有很好的隐蔽性且功耗较低,能够长期铺设在海底,对水面及水下目标进行探测、定位等。基于被动声呐的这些优点,研究近程运动目标被动定位方法。被动定位方法有三元阵被动测距方法、目标运动分析(Target motion analysis,TMA)和匹配场处理(Matched field processing,MFP)、时间反转镜(Time reversal mirror,TRM)、近场声全息技术(Near-field acoustical holography,NAH)、声图测量法等。三元阵被动定位方法在400 m 以内的近距离定位误差较大[1],且目标距离越近,其定位性能越差[2]。TMA[3−4]和MFP[5]都属较成熟的远程定位方法,立意于提高作用距离和降低检测门限,不关注于近场。TRM 在被动定位技术上的应用尚不成熟,且定位精度不高。NAH[6]针对的是极近距离声场分析,不适用于中近距离目标的跟踪定位。声图测量方法[7−8]对百米距离范围内的目标有较高的被动定位精度,目前大多学者主要研究线阵或十字阵被动定位,且主要关注极近距离、中低频目标,主要用来测量舰船等某部位的辐射噪声源位置[9]。本文以声图测量方法为基础,采用组合线阵宽带最小方差无畸变失真响应(Minimum variance distortionless response,MVDR)聚焦波束形成技术,实现近场水下小目标的高精度被动定位。
直线阵是基阵信号处理中最常用的阵型结构,这是由于直线阵阵型结构简单,易于数学上的处理。但是直线阵在对目标进行定位时,存在左右弦模糊问题,本文采用横竖相间的组合线阵来克服此问题。阵列孔径越大定位精度越高,而水下大型半波间距阵布放代价很大,本文针对水下非合作目标出现的实际区域,采用稀疏布阵方式,结合宽带信号处理方法,克服阵列稀疏带来的影响。滤波与预测是TMA 算法的核心,其中卡尔曼(Kalman)滤波[10]是典型的线性无偏最小方差估计器,本文针对运动近程目标,结合卡尔曼滤波对目标位置进行估计,并采用目标轨迹匹配算法,实现对运动目标的跟踪定位。
1 组合线阵近场测量模型
利用均匀声压线阵对近程目标进行定位时,聚焦波束形成的纵向分辨率较低,且在实际测量中不能保证目标处于线列阵的开角范围内。同时,利用单条线列阵进行噪声源的定位时会产生左右舷模糊问题,这些会导致以上定位方法的性能急剧恶化,甚至不能正确判别噪声源的位置。采用互相垂直的多条线阵能有效解决以上问题,抑制左右舷模糊,提高定位性能。
如图1所示,1号、3号、5号阵为位于x轴的水平线阵,2 号、4 号阵为垂直于x轴的线阵,1 号阵的左侧第一阵元位于坐标原点,相邻阵列间距为D。每条子阵由M个阵元组成,阵元间距为d,各阵元的位置坐标为(xmi,ymi,0)(mi=0,··· ,M;i=1,··· ,5),总阵元数为5M。以原点处的阵元为参考阵元,第p号声源与参考阵元间的距离为d,第p号声源(xp,yp,zp)距离其他阵元的距离矢量和时延矢量为
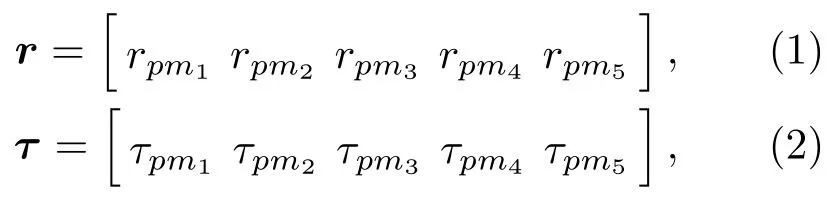
其中,
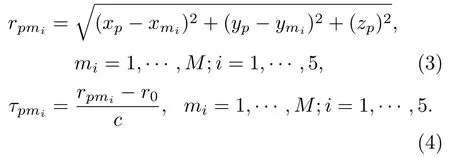
第p号声源对应的维方向向量为
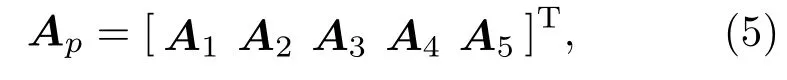
式(5)中,Ai=[e−j2πfjτpmi]T(mi=1,··· ,M;i=1,··· ,5)。
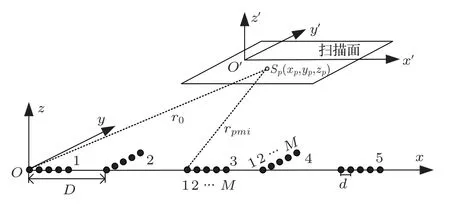
图1 组合线阵目标近场测量模型Fig.1 Combination linear array target measurement model
2 组合线阵近场定位原理
近场聚焦波束形成是将一定几何形状排列的多元阵,按球面波扩展方法对各阵元接收到的信号进行时延或相移补偿处理,当补偿到声源位置处时,各阵元接收信号会形成同相迭加,出现“聚焦”点,聚焦峰对应的空间位置即为声源位置。
当组合线阵的近场区域存在P个声源,声源辐射信号为sp(t)(p=1,··· ,P),第m号阵元接收信号Bm(t)为

式(6)中,Ap表示声源功率,rpm为声源sp到第m号阵元之间的距离,τpm=rpm/c为相应的传播时延。
将阵列接收信号分为L个子段,每段为∆T,对阵元接收数据做J点离散傅里叶变换(Discrete Fourier transformation,DFT),得到宽带信号模型:

式(7)中,Xl(fj)、Sl(fj)、Nl(fj)分别对应频率fj的接收数据、信号和噪声的DFT变换。
第p个声源对应的方向向量为

以基于幅度补偿的MVDR[11]的近场聚焦波束形成为基础,得到组合线阵输出的空间谱为
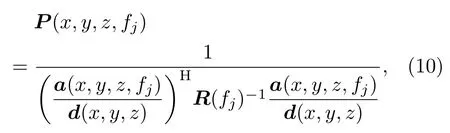
式(10)中,

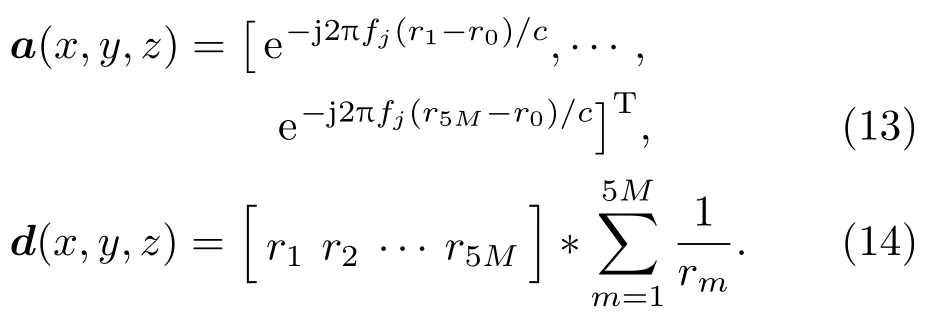
依照多重信号分类方法,对协方差矩阵R(fj)进行修正,首先对其进行奇异值分解其中U、V的列向量为R(fj)的左奇异向量与右奇异向量;S=diag(σ1,··· ,σP);N=diag(σP+1,σP+2,··· ,σ5M),σ1,σ2,··· ,σP,σP+1,σP+2,··· ,σ5M为R(fj)的奇异值,可以反映信号和噪声能量集中情况,将反映噪声的奇异值置零,能去除信号中的噪声[12]。对协方差矩阵进行重构,得到采用重构后的协方差矩阵进行聚焦波束形成,进一步抑制了噪声干扰,提高目标定位精度。
3 目标跟踪方法
目标跟踪是指计算机或其他仪器设备依据某种算法实现对目标的跟踪与定位,并根据目标的位置和动向采取相应措施。通过上述波束形成方法得到目标位置信息,采用阈值检测、卡尔曼滤波及跟踪方法实现目标的连续跟踪[13]。由于水声环境的复杂,定位结果经常会受环境噪声影响出现不确定的中断和野值,严重影响目标定位跟踪,本文根据卡尔曼滤波预测目标当前时刻位置,确保不会因为目标漏检而跟踪中断。
卡尔曼滤波利用前一时刻的估计值和当前时刻的观测值得到当前时刻的状态估计值。设目标在n时刻位置为(x,y),vx、vy分别为目标的运动速度,则目标的运动特性为

目标的状态矢量为Xn=[x(n),y(n),vx,vy]T,状态转移函数An=,可以对目标位置做出有根据的预测,即使伴随着水下环境干扰,卡尔曼滤波总能指出目标的最真实位置。
卡尔曼滤波递推公式为
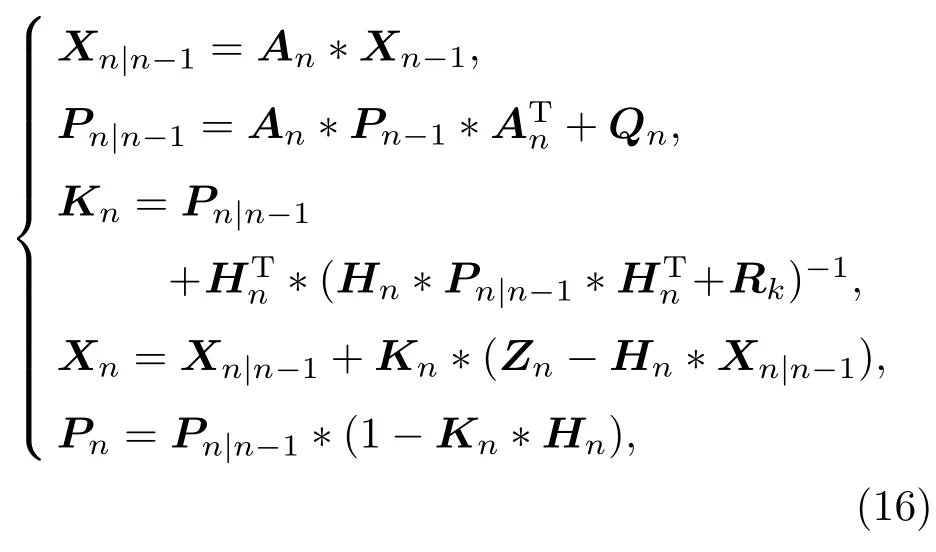
式(16)中,Xn|n−1为预测状态矢量;Pn|n−1为预测误差的方差矩阵;Qn为量测噪声;Rk为测量噪声的方差矩阵;此处观测值为(x,y),聚焦波束形成得到目标位置Zn=(xn,yn)作为测量输入,假设目标做匀速运动,观测矩阵
目标跟踪算法流程如图2 所示。目标跟踪算法的核心思想是:
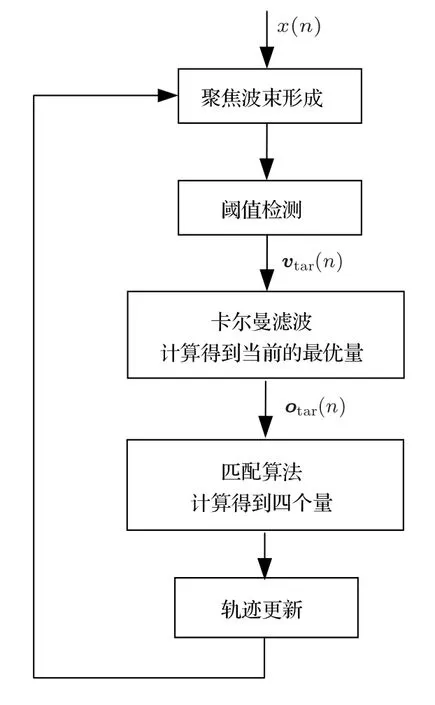
图2 目标跟踪算法流程Fig.2 The flow of target tracking algorithm
(1)对当前快拍(帧)的数据x(n)进行聚焦波束形成,通过阈值检测到所有可疑目标的位置,即当前帧的目标位置观测值vtar(n)。
(2)根据当前帧vtar(n)和上一刻的估计值ftar(n −1)和”误差”Etar(n −1),通过卡尔曼滤波得到当前帧的运动目标位置“最优量”otar(n)。同时再预测下一帧的目标位置ftar(n)。
(3)在每帧中得到“最优量”otar(n)与之前正在跟踪的目标轨迹T(k)关联起来,通过设置四个量来记录当前帧中轨迹和检测到的目标“最优量”匹配结果:
DUnassigned:otar(n)与所有正在跟踪的K条轨迹T(k)(k=1,2,··· ,K)都不能匹配;
DAssigned:otar(n)能匹配到某条轨迹T(k);
TUnassigned:匹配不到otar(n)的轨迹T(k);
TAssigned:匹配到otar(n)的轨迹T(k)。
(4)计算跟踪轨迹上一帧位置和当前帧otar(n)之间的距离,若距离在但一定的范围内,说明目标持续存在,将距离计算结果作为损失函数矩阵,再使用匹配算法,根据预设的阈值计算得到DUnassigned、DAssigned、TUnassigned、TAssigned。
(5)轨迹更新:将DAssigned更新至当前帧的TAssigned位置;由于各种干扰导致目标漏检,目标可能在几帧后再次被检测到,预设一个阈值为最大不可见长度LInvisible,若连续LInvisible次没有被检测到,删除该目标轨迹,停止跟踪,否则轨迹依旧继续跟踪;将达到阈值的TUnassigned删除;将DUnassigned生成新的跟踪轨迹,当前帧DUnassigned可能是新的目标,也可能是噪声引起的野值,预设一个最小可见次数LVisible,若持续LVisible帧都能检测到,确定目标存在,输出目标位置。
4 仿真实验
4.1 目标定位仿真分析
假设有5条16元1.5 m间距线阵,3条水平摆阵与2 条垂直摆放,总阵元数为80,两相邻阵列(首阵元)间距为45 m;以第1 条阵1 号阵元为坐标原点,仿真信噪比SNR=0 dB,100∼500 Hz的宽带目标信号,设置目标在组合阵的不同位置,得到的定位结果如图3所示。
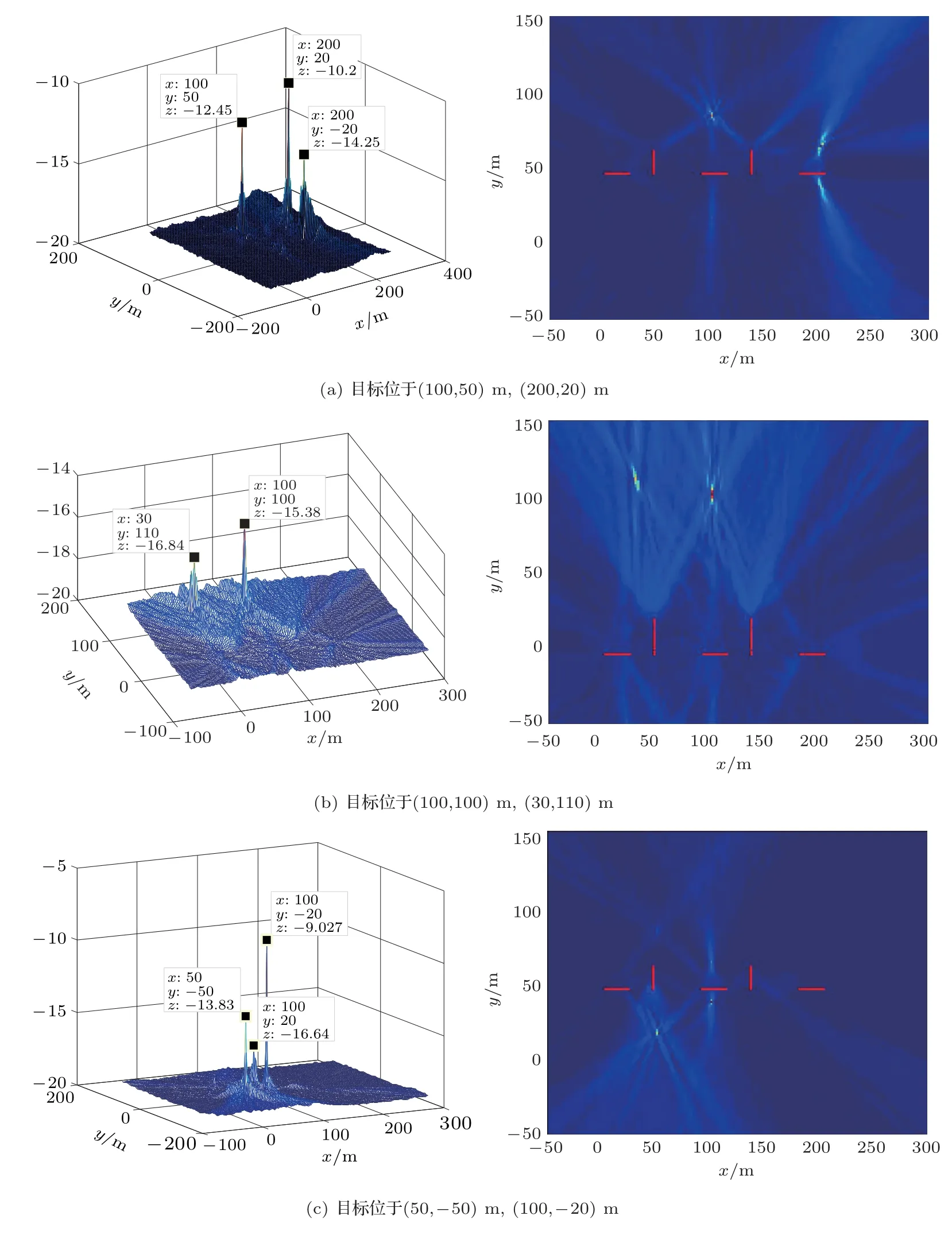
图3 不同位置目标定位结果图Fig.3 Location result of targets in different positions
4.2 信噪比对定位结果的影响
对位于(100,100)m 处的目标进行定位,定位误差随信噪比变化曲线如图4 所示,并对每个信噪比进行1000次蒙特卡洛独立实验。
4.3 卡尔曼滤波预测结果分析
根据4.2 节得到的定位误差随信噪比变化曲线,生成一条SNR=−15 dB 的目标运动轨迹,即目标的坐标位置信息,为当前时刻的“测量值”,卡尔曼滤波根据当前帧的“测量值”和上一帧得到的“预测值”与“误差”计算得到当前帧的最优位置,并预测下一帧计算需要的“预测值”。原始轨迹与卡尔曼滤波后的轨迹如图5 所示,加随机噪声后的位置平均误差为2.55 m,卡尔曼滤波后位置平均误差1.42 m。
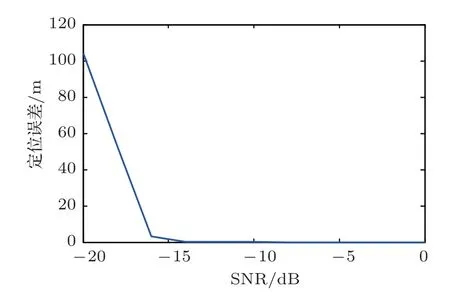
图4 信噪比变化对定位的影响Fig.4 The influence of signal-to-noise ratio change on location
综合上述仿真,得出以下结论:
(1)目标距离阵越近,定位效果越好;
(2)本文的组合线阵能有效抑制左右舷模糊,但当目标距离某条阵很近时,仍然有左右舷模糊影响,可以从空间谱幅度上分辨出目标真实位置;
(3)即使目标不在某条阵的有效探测范围(−60◦∼60◦)内,组合线阵也能准确地定位到目标;
(4)随着信噪比的增加,定位误差减小,当信噪比SNR =−15 dB 可以准确对百米范围内目标进行定位;
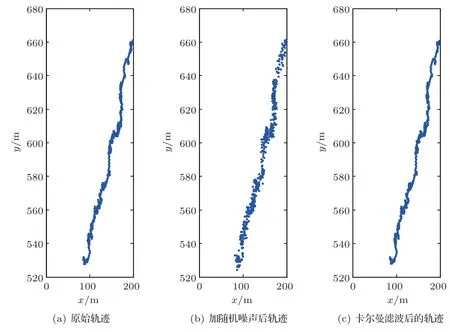
图5 卡尔曼滤波预测效果图Fig.5 Prediction effect of Kalman filter
(5)环境噪声过大对定位结果有一定的影响,定位出现偏差不利于目标的连续跟踪,卡尔曼滤波在一定程度上能抑制环境的影响,得到较为正确的目标位置。
5 海试试验数据处理
本文用到的试验数据是于2018年6月在渤海海试采集,试验目的是利用组合线阵对水下蛙人小目标进行定位与跟踪。试验概况:试验地点水深为3∼4 m,5 条阵元间隔为1.5 m 的16 元声压水听器构成的均匀线阵,相邻阵列距离45 m。蛙人(如图6所示)从距离3 号阵50 m 左右的位置下潜,垂直向3号阵游动。阵元坐标位置的准确与否,关系到目标定位效果的好坏。为实现目标的高精度定位,减少阵元位置误差和幅相误差,阵列布放后,对阵元坐标位置进行标定,通过阵列校正技术解决阵列误差引起的导向矢量失配问题。

图6 试验用蛙人Fig.6 Experimental frogman
分析试验用蛙人的拉锯试验数据进行时频分析,结果如图7 所示。图7(a)为蛙人由远处向阵游的时频分析结果,图7(b)为蛙人远离阵的时频分析结果。蛙人的时频图具有明显的周期性,约为3 s,与蛙人呼吸频率有关。蛙人离阵较远时能量较弱,离阵较近时能量强。图7(a)时间段带内信噪比由低变高,约从−9.6 dB变化至−1.4 dB。
选取蛙人下潜后某一时刻的试验数据,采用本文定位方法得到的结果如图8所示。
选取图7(a)段数据,对目标进行定位跟踪,阈值设置为LInvisible=10、LVisible=5,跟踪结果如图9 所示,“◦”表示某时刻测得的目标位置。图9(a)为不加卡尔曼滤波的跟踪结果,跟踪中出现间断,图9(b)使用卡尔曼滤波后,能对目标进行连续的跟踪定位。
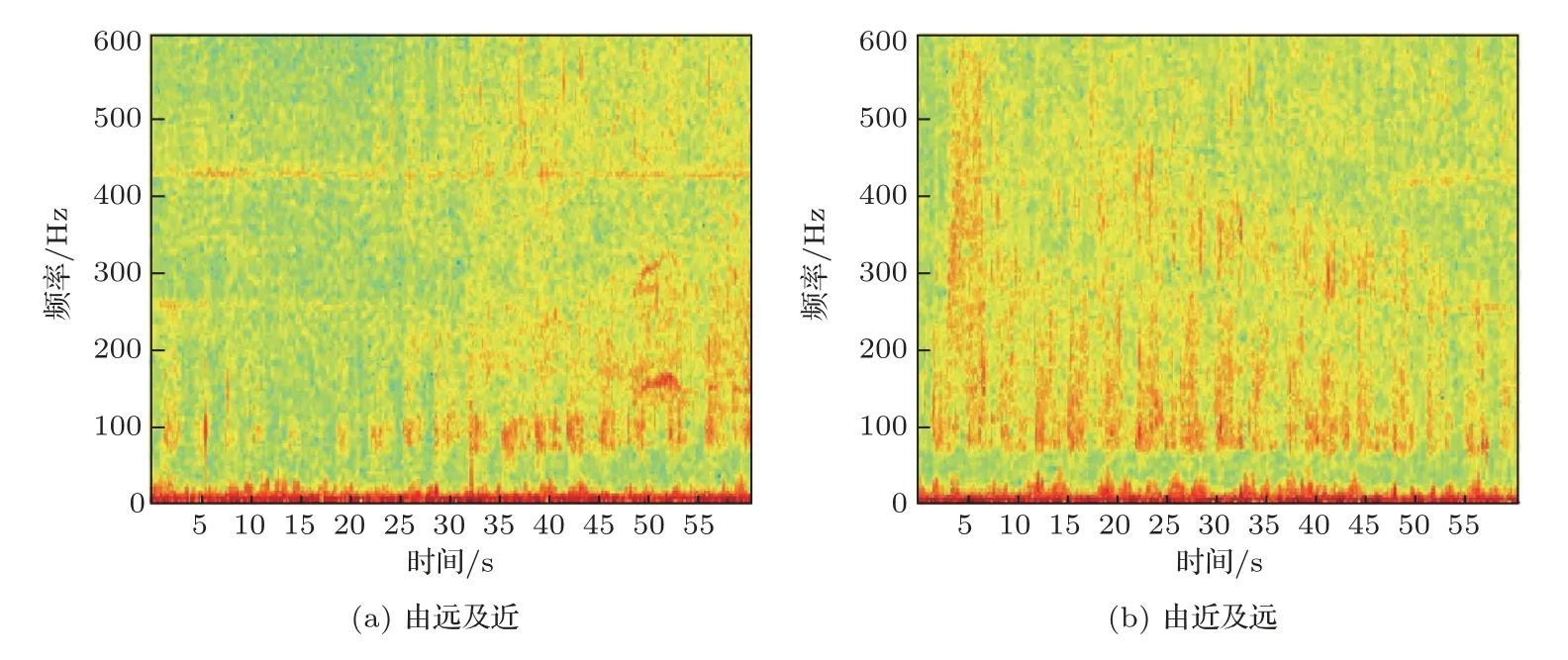
图7 时频分析结果Fig.7 Time-frequency analysis results
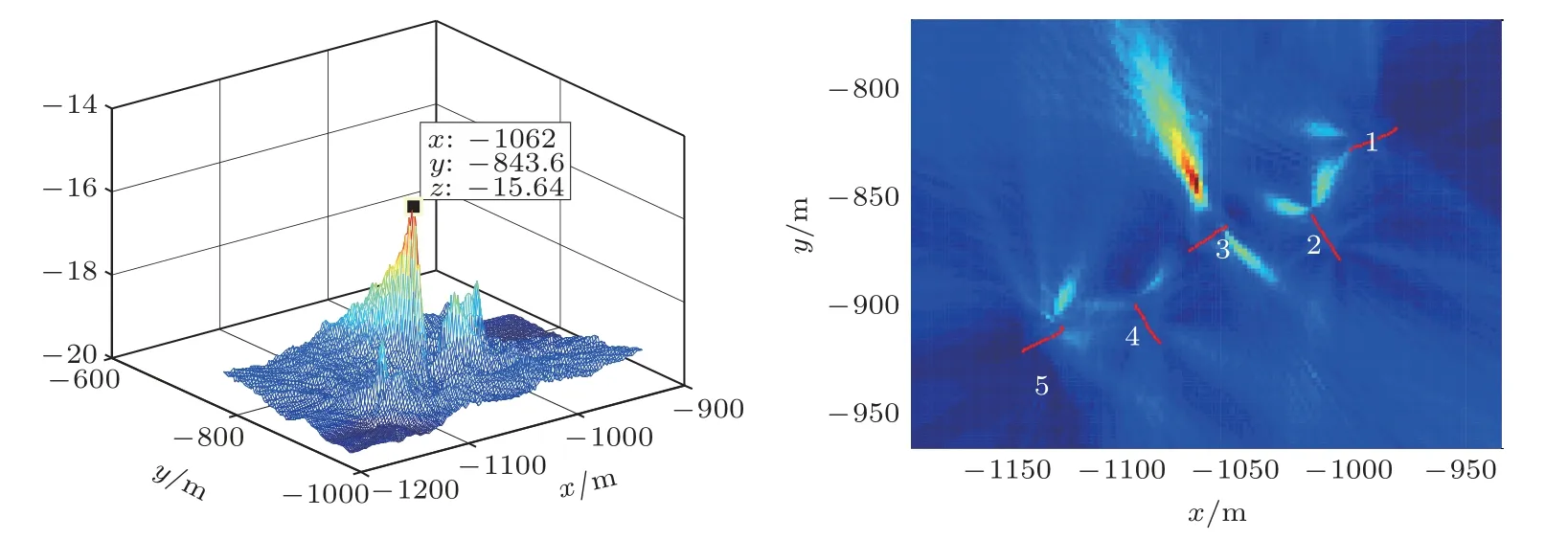
图8 试验数据目标定位结果Fig.8 Target location result of test data
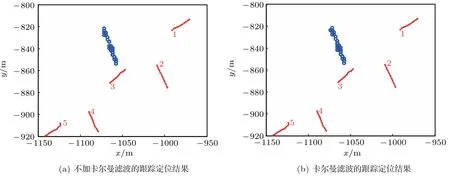
图9 试验数据目标跟踪结果Fig.9 Target tracking result of test data
6 结论
本文基于组合线阵,采用修正的宽带MVDR聚焦波束形成技术,实现近场目标的高精度被动定位,在一定程度上有效地抑制了左右弦模糊。并结合卡尔曼滤波跟踪方法,实现了对近程运动目标的跟踪,本文方法可用于近程小目标实时被动定位跟踪系统。
