平原河网区河道交汊口分流特性模型试验研究
2020-03-10刘国庆范子武穆守胜贾本有乌景秀
刘国庆,王 蔚,范子武,穆守胜,贾本有,乌景秀,邓 曌
(南京水利科学研究院 水文水资源与水利工程科学国家重点实验室,江苏 南京 210029)
平原河网区分汊河道是一种极为常见的河型。研究分汊口的分流特性,对于保障区域防洪排涝、供水、通航安全,保护河流水环境健康,指导水利工程建设等具有十分重要的现实意义。依据干、支流河床平面形态,分汊河道可以分为“Y”型交汊口(对称式交汊口)和斜接形交汊口[1-3]。我国关于分汊口分流特性的研究,按照研究对象,可大致分为两类。一类是针对大江大河的重要分汊口,例如:长江口南北汊、珠江口思贤滘等。张蔚等利用平面二维数学模型,定量分解出径流、潮流和径潮相互作用对长江口南北汊分流比的影响[4]。杨清书等利用珠江口思贤滘三水、马口站实测水文资料,探讨近几十年来西北江三角洲河网区顶点分水分沙的季节变化和多年变化[5]。另一类则是针对自然及人工河道中常见的直角分水口和弯道分水口的研究。罗福安等利用水槽试验,研究了直角分水口口前水流的运动形态,揭示了分水宽度沿水深的变化规律[6]。郭维东等在物理模型试验基础上,结合三维数学模型,研究了弯道取水口流态和流速分布,分析了不同取水角度引水口上游分水宽度及分流比的变化规律[7-8]。总体看来,对于分汊河道的研究,国内外学者大多重点关注交汊口水流流态、水沙物质分配及其影响因素等相关问题[9-12]。
苏南运河作为太湖流域唯一跨越多个水利分区的南北向河道,起着水量调节和承转作用,直接影响沿线流域、区域及城市防洪排涝安全。2015,2016,2017年苏南运河沿线连续出现超警戒、超历史的洪水,一直以航运为主要任务的苏南运河成了流域内“涨水快、退水慢、水位高”的高水位河道,是本区域洪水风险防控的重点。然而,目前针对苏南运河沿线分汊口流态、分流比及影响因素等相关研究相对较少。由于苏南运河自身下泄能力有限,洪水主要依靠沿线相连的通江河道外排入江,但各段通江河道与运河连接间的交汊角存在差异,使得大运河洪水入江走向有顺水流与逆水流方向;加之运河沿线苏、锡、常城市防洪大包围建成,切断了部分骨干入江河道。另外,洪水入江还受区域圩区群建设、入江口门规模与调度等因素影响,如何妥善解决太湖流域洪水出路需要从流域全局进行整体研究。
苏南运河-蠡河-望虞河交汊口既是苏南运河沿线重要的分洪通道,又是流域、区域洪水遭遇的典型位置。以苏南运河-蠡河-望虞河典型分汊口为研究对象,通过开展相关物理模型试验研究,为工程建设、工程调度及数值模拟提供理论指导,为运河沿线排江通道分流能力及外排能力的匹配研究提供理论支撑。以“16·7”超历史洪水实测资料为基础,建立研究区域平面二维数学模型,研究超历史洪水条件下蠡河分流比及其变化过程,并从流量、上下游水位差以及分流角度等方面揭示苏南运河-蠡河-望虞河分汊口分流比的影响因素。
1 区域概况
苏南运河-蠡河-望虞河交汊口位于望亭立交水利枢纽工程处,望虞河经由望亭立交工程下穿苏南运河(图1)。望亭立交与苏南运河成60°交角,地涵有9孔,每孔高6.5 m,宽7.0 m,均有闸门控制。蠡河位于望亭立交上游东侧,上通苏南运河、下接望虞河,全长约500 m,是苏南运河重要的排江通道。蠡河枢纽在运河高水位时可分泄苏南运河洪水入望虞河,降低苏南运河水位减缓区域防洪压力,是区域防洪重点工程之一。现状蠡河枢纽工程由船闸与节制闸组成,节制闸闸孔净宽8 m,船闸宽8 m,长135 m。
望虞河位于太湖流域阳澄淀泖区和武澄锡虞区的交界处,是流域综合治理骨干工程之一,总长60.8 km,既是流域洪水外排长江的主要河道,又是太湖流域“引江济太”的重要调水通道(图1)。望虞河入太湖湖口由望亭立交水利枢纽控制,入长江口由常熟水利枢纽控制。望虞河东岸沿线大小支流众多,多由闸门控制,引江济太期间大部分处于关闭状态;西岸属典型的平原河网区,支流多兼排地区涝水,仅北部靠近长江的福山塘以北段和南部嘉菱荡以南段由闸门控制,其余均为敞开状态[13-14]。
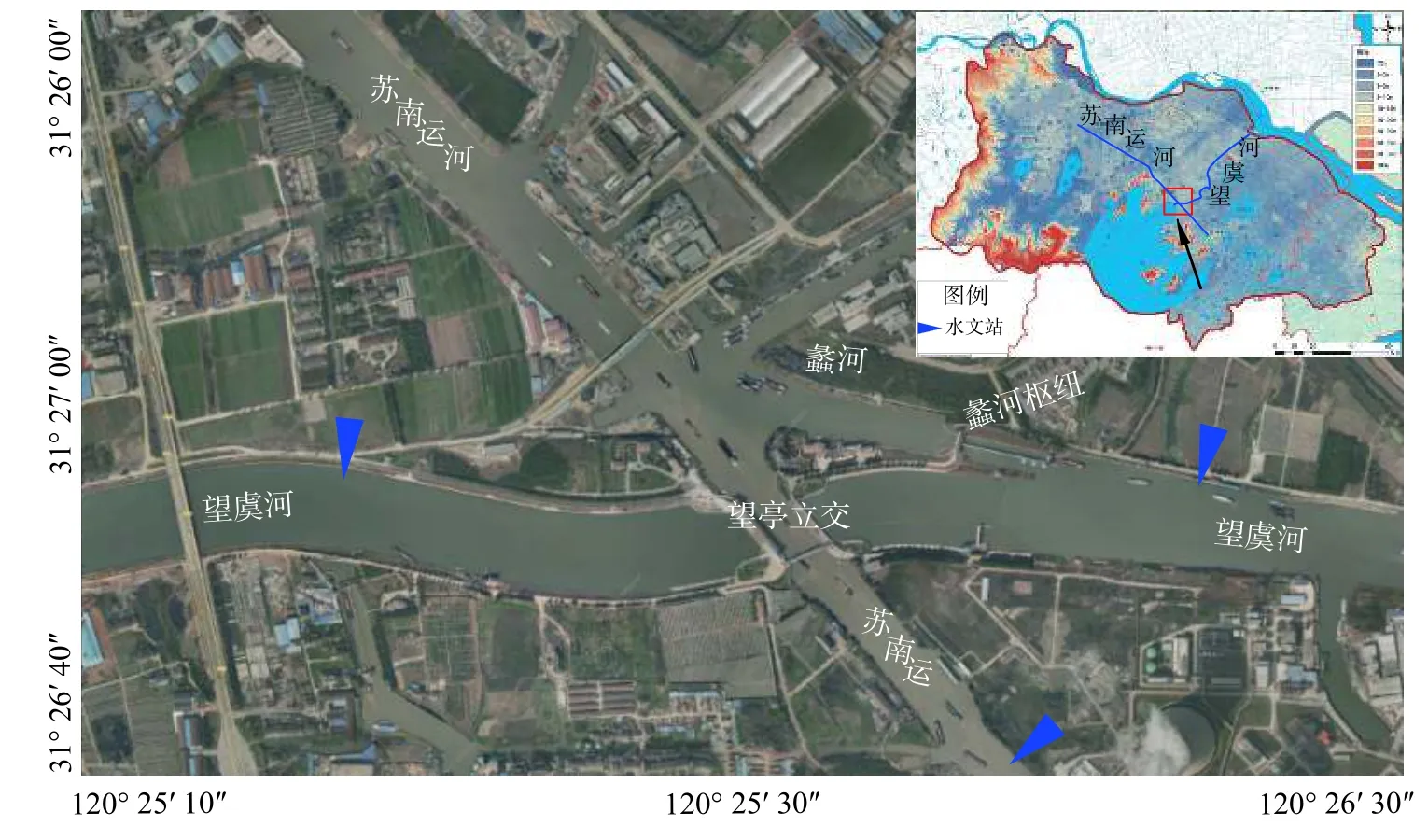
图 1 苏南运河-蠡河-望虞河分汊口平面图Fig. 1 Junction of South Jiangsu Canal-Li River-Wangyu River
2 研究方法
基于江苏省太湖地区整体一维河网数学模型与苏南运河-蠡河-望虞河交汊口局部物理模型,进一步建立了苏南运河-蠡河-望虞河交汊口局部平面二维数学模型。江苏省太湖流域整体一维河网数学模型范围为江苏省太湖地区,面积约为1.96万km2,包括苏州、无锡、常州市的全部和镇江市的部分区域,模型通过“15·6”,“16·7”,“17·9”等多组典型洪水验证。交汊口二维数学模型计算边界由区域整体一维河网数学模型提供,采用实测资料及物理模型交叉验证的方法对二维数学模型水位、流量等计算结果进行验证。利用验证后的苏南运河-蠡河-望虞河交汊口局部平面二维数学模型,模拟计算“16·7”超历史洪水过程蠡河枢纽调度前后交汊口主要位置处水位、流量变化过程,分析蠡河枢纽现状分流比及其影响因子;进一步计算苏南运河-蠡河不同交汊角度对蠡河分流的影响,并探讨其成因。
2.1 交汊口局部物理模型
苏南运河-蠡河-望虞河交汊口局部物理模型按水流运动相似、重力相似及阻力相似准则要求设计,采用比尺为1∶30的正态模型。模型上边界为望亭立交苏南运河上游0.6 km、望虞河上游0.8 km处;下边界为望亭立交苏南运河下游0.4 km、望虞河下游0.6 km处,模型还包括望亭立交水利枢纽、蠡河水利枢纽工程及蠡河(图2)。

图 2 苏南运河-蠡河-望虞河分汊口局部物理模型Fig. 2 Partial physical model of South Jiangsu Canal-Li River-Wangyu River junction
2.2 交汊口平面二维水流数学模型
利用MIKE21工程软件包建立苏南运河-蠡河-望虞河交汊口局部平面二维数学模型。MIKE21是二维自由水面流动模拟系统软件,可运用于自由水体流动、污染物扩散以及泥沙输运等二维数值模拟研究。苏南运河-蠡河-望虞河交汊口局部平面二维数学模型范围,以望亭立交为中心,上边界分别控制到苏南运河上游2.6 km、望虞河上游2.0 km处,下边界分别控制到苏南运河下游2.8 km、望虞河下游2.1 km处。模型整体采用非结构三角形网格,网格最大空间步长为15 m,交汊口处局部加密至5 m,最终节点总数为23 689个,网格总数为44 666个。模型地形采用2018年交汊口范围内1∶500实测地形,上边界采用流量控制,下边界采用水位控制,边界条件由区域整体一维河网数学模型提供。蠡河枢纽采用MIKE21中水闸模块进行模拟,苏南运河与望虞河立交断面则采用管涵模块实现准确模拟。
模型验证与计算水文组合均选取“16·7”超历史洪水过程,结合《苏南运河区域洪涝联合调度方案》(苏防办电传(2016)85号),具体计算时间为蠡河枢纽启用后的36 h,即2016-07-02T07:00—2016-07-03T18:00。苏南运河-蠡河-望虞河交汊口实测水文资料相对缺乏,因此,本文利用了“16·7”实测望亭上、望亭下及望亭(大)3个站点(位置见图1)的水位,局部物理模型测得的“16·7”蠡河枢纽启用后蠡河流量过程对二维水流数学模型的水位、流量进行验证,验证结果见图3。由图3可见,计算值与实测水位值及物理模型观测流量值吻合良好,水位误差均在0.05 m以内,流量误差一般都在10%以内,表明二维数学模型较为真实地模拟了交汊口水流运动特征,可应用于本次研究工作。
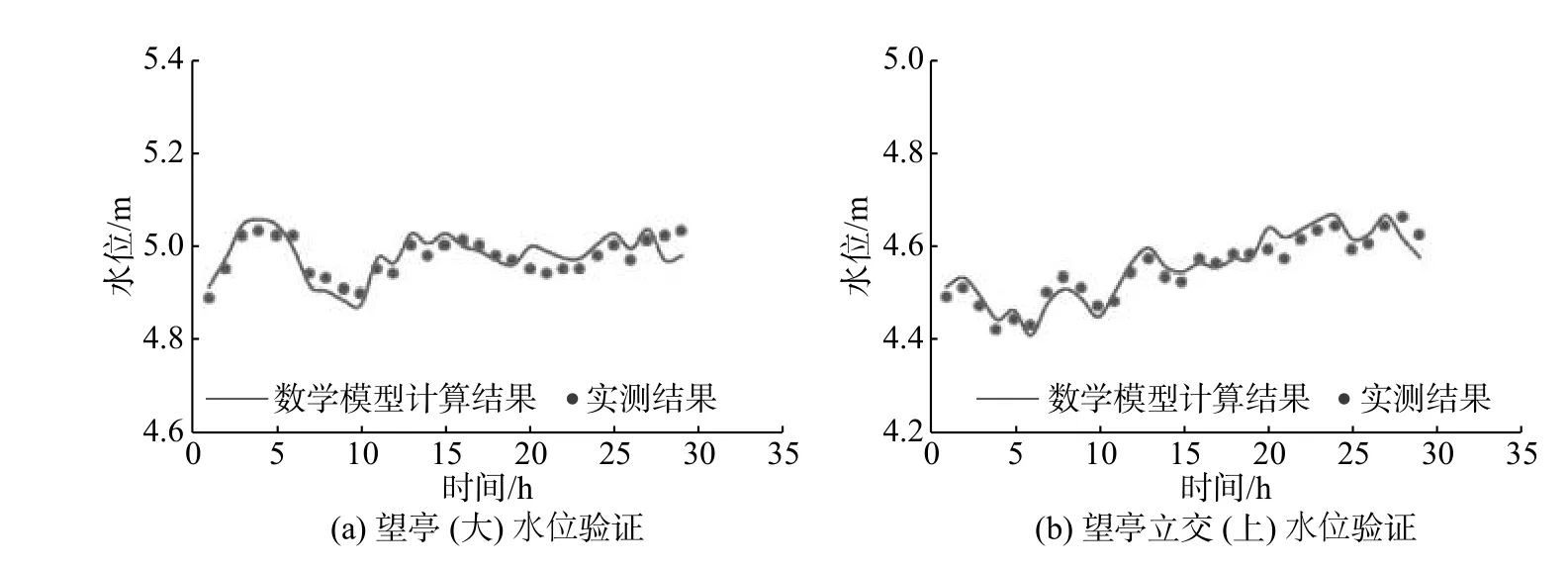
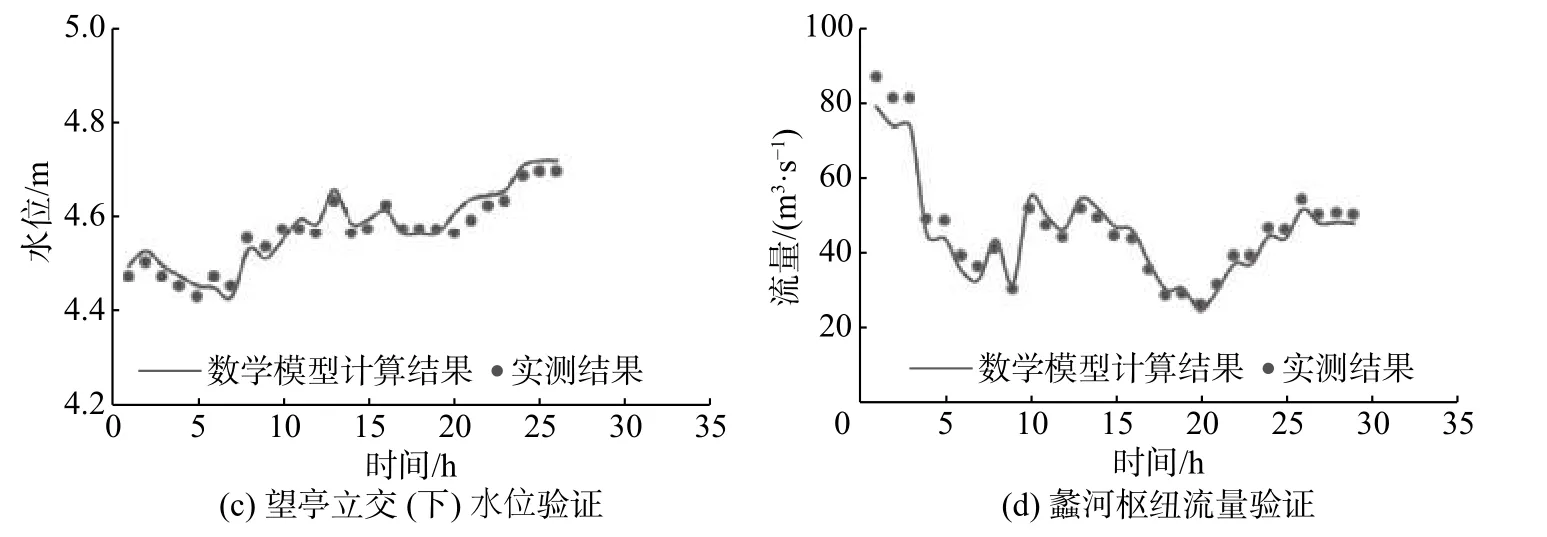
图 3 交汊口局部平面二维数学模型水位、流量验证结果Fig. 3 Verification results of water level and discharge of the two-dimensional mathematical model
2.3 模型计算方案设计
方案设计考虑现状交汊角度分流特性计算方案与变交汊角度影响分析计算。现状交汊角度分流特性分析方案的计算时段为蠡河枢纽启动前24 h至启动后36 h,即:2016-07-01T07:00—2016-07-03T18:00。模型计算完成后,统计蠡河枢纽启用后30 h内苏南运河流量、蠡河流量、苏南运河水位(苏南运河-蠡河交汊口位置)、望虞河水位(望虞河-蠡河交汊口位置)变化过程,分析蠡河流量及分流比变化过程及影响因素。
变交汊角度影响分析方案的计算时段、控制边界及模型参数与现状交汊角度分流特性分析方案完全一致,仅将现状苏南运河-蠡河交汊角度(约35°)分别改变至20°,45°,60°,90°和120°,统计蠡河枢纽启用后30 h内蠡河流量变化过程,分析交汊角度对蠡河分流比的影响并分析其原因。
3 交汊口分流特性分析
3.1 蠡河流量及分流比变化分析
图4为蠡河枢纽启用后蠡河分流量与分流比随时间变化。由图4可见,枢纽启用后,蠡河流量变化过程与分流比变化过程基本一致。枢纽刚启用时,苏南运河与望虞河水位差最大,因此过闸流量最大,蠡河流量约为73 m3/s,分流比约为52%。在随后的近20 h内,蠡河流量及分流比总体呈现波动下降趋势,原因是由于随着蠡河泄洪,苏南运河与望虞河水位差逐渐减小。最后蠡河泄流量又回升至48 m3/s,分流比上升至30%左右并基本保持稳定。

图 4 蠡河流量分流比变化Fig. 4 Variation of diversion ratio of Li River
3.2 苏南运河流量对蠡河分流比的影响
根据以往相关研究成果,支流分流比多与干流来流量密切相关,本次研究绘制了苏南运河流量与对应时刻蠡河分流比散点分布图(图5)。由图5可见,散点分布散乱、规律性较差,因此对于苏南运河-蠡河交汊口而言,干流苏南运河的来流量对支流蠡河的分流比影响不大。分析其原因,对于天然的“Y”型交汊口或者斜接形交汊口,其支流的分流比多与干流流量有关,而苏南运河-蠡河-望虞河交汊口是不同于以上两种交汊口形态的较为特殊的交汊口,蠡河枢纽启用时,其过闸水头主要由望虞河与苏南运河水位差所决定,因此,蠡河分流比可能与蠡河枢纽闸下水位(即望虞河出口段水位)及苏南运河-望虞河水位差有关。
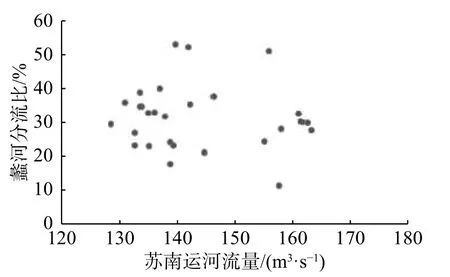
图 5 苏南运河流量与蠡河分流比关系Fig. 5 Relationship between discharge of South Jiangsu Canal and diversion ratio of Li River
3.3 望虞河水位对蠡河分流比的影响
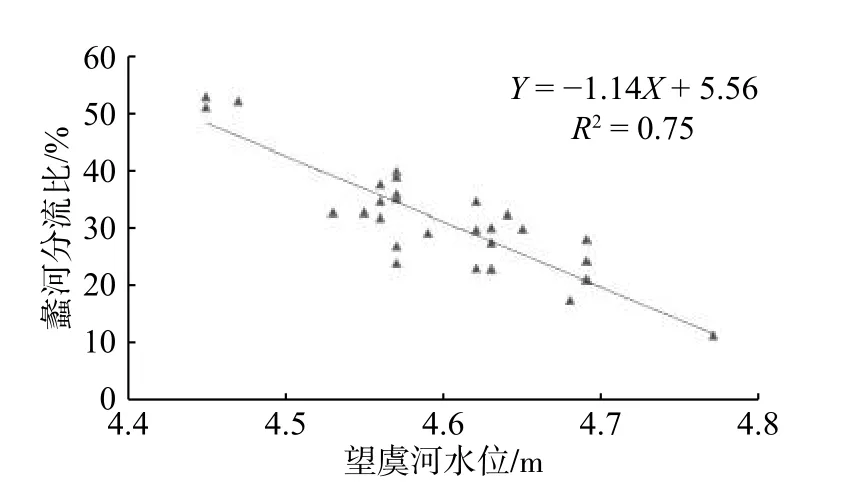
图 6 望虞河水位与蠡河分流比关系Fig. 6 Relationship between water level of Wangyu River and diversion ratio of Li River
蠡河分泄的洪水直接进入望虞河,因此望虞河蠡河出口段水位可能对蠡河分流比产生影响。本文利用数学模型计算结果,建立了蠡河枢纽启用后,望虞河水位与蠡河分流比关系(图6)。如图6所示,蠡河分流比随着望虞河水位升高而减小,二者呈现近似线性负相关关系,即:其中:Y为蠡河分流比;X为望虞河水位。这主要是由于望虞河水位升高会导致蠡河枢纽闸下水位壅高,在苏南运河水位不变的情况下,蠡河枢纽过闸水头减小,导致蠡河分流比相应减小。
3.4 苏南运河-望虞河水位差与蠡河分流比的相关性分析
为进一步探究蠡河分流比的影响因素,建立苏南运河-望虞河水位差与蠡河分流比的关系。由图7可见,蠡河枢纽分流比随苏南运河-望虞河水位差增大而增大,且二者呈现很好的线性正相关关系,即:其中:Y为蠡河分流比;X为苏南运河与望虞河水位差。这是因为蠡河枢纽泄流量大小直接由其过闸水头决定,而蠡河枢纽的过闸水头又由苏南运河-望虞河水位差决定,因此蠡河枢纽启用后其分流量及分流比均由苏南运河-望虞河水位差决定。

图 7 苏南运河-望虞河水位差与蠡河分流比关系Fig. 7 Relationship between water level difference of South Jiangsu Canal-Wangyu River and diversion ratio of Li River
3.5 交汊角度对蠡河分流比的影响
现状苏南运河与蠡河河道中心线夹角约为35°,为了研究分流角度对蠡河分流比的影响,本文进一步计算了另外5组夹角,分别为20°,45°,60°,90°,120°,蠡河枢纽启用时,蠡河的分流比变化过程(图8)。当苏南运河与蠡河交角不同时,蠡河分流比大小及变化过程基本一致,这表明苏南运河与蠡河的交汊角度对蠡河分流比基本无影响。
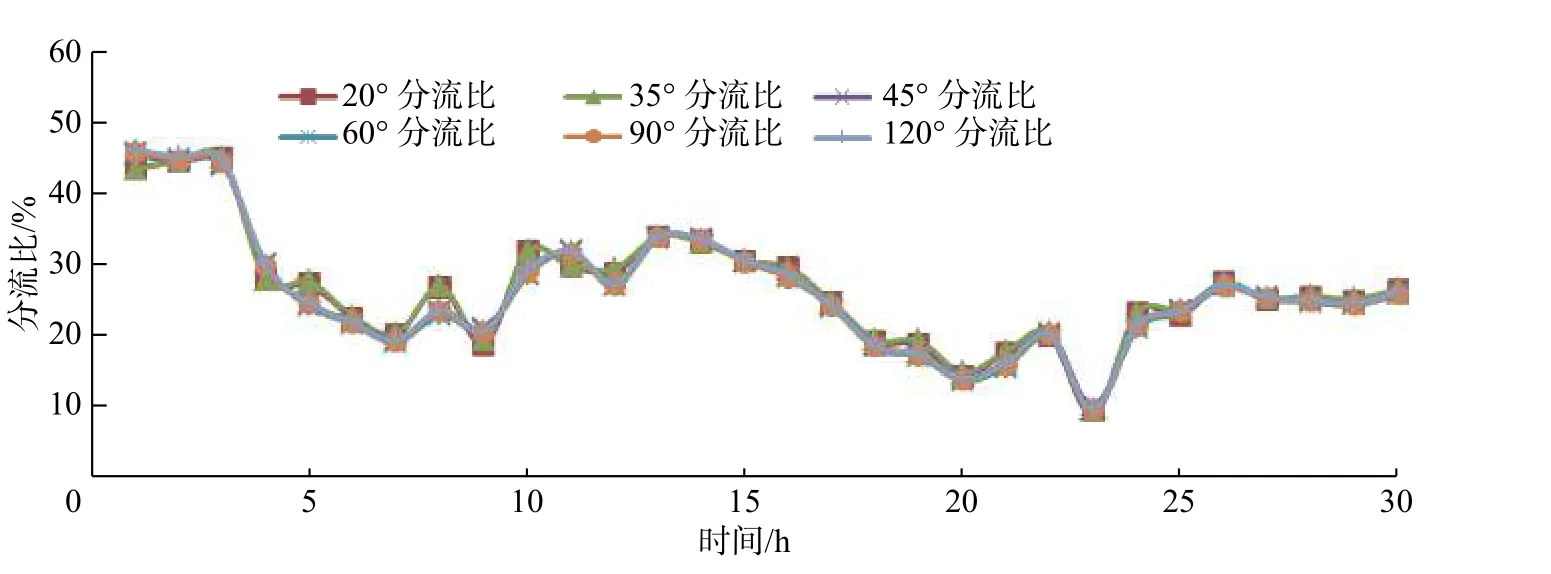
图8 不同分流角度蠡河分流比变化过程Fig.8 Changes of Li River diversion ratios under different diversion angles
当干流内水流流经分水口后,部分水流发生偏转进入支流,并且会在支流一侧形成回流区,导致进水口的实际宽度要小于支流宽度,回流区在干流方向的宽度越大,对支流的有效过流宽度影响越大[8]。图9为苏南运河-蠡河交汊口不同分流角度下,蠡河水闸启用后交汊口流态。由图9可见,当交汊角分别为20°,35°,45°,60°,90°和120°时,蠡河口门区均有明显的回流区存在,且不同交汊角度下回流区大小及强度基本相当,造成不同交汊角度下蠡河的分流量及分流比基本保持不变。
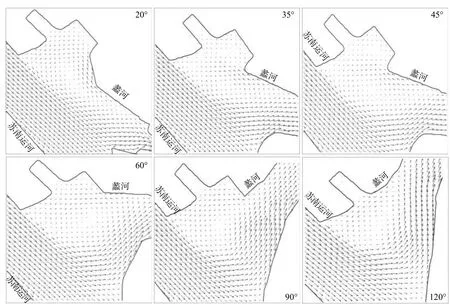
图 9 不同分流角度分汊口流态Fig. 9 Flow patterns under different diversion angles
4 结 语
平原河网区河道交汊口分流特性一直都是学术界高度关注的问题。以苏南运河-蠡河-望虞河典型交汊口为研究对象,利用平面二维数学模型,研究了苏南运河流量、望虞河水位、苏南运河-望虞河水位差以及分汊口角度对蠡河分流比的影响,主要结论如下:
(1)苏南运河-蠡河-望虞河交汊口不同于常见“Y”型或者斜接形交汊口,干流苏南运河的流量对蠡河分流比影响较小。
(2)蠡河分流比与望虞河水位及望虞河-苏南运河水位差密切相关,蠡河分流比与前者呈现近似负线性相关,与后者则呈现较好的正线性相关。
(3)苏南运河-蠡河交汊角度对蠡河分流比影响不大,这主要是由于口门回流区降低了支流有效过水宽度,导致进水口的实际过流宽度小于支流宽度。
苏南运河沿线分流节点众多,且受人为干预较大,其分流特性往往由流域水情及水利工程调度共同决定。因此,综合考虑流域、区域防洪需求,科学制定流域、区域防洪工程调度方案,优化枢纽改扩建工程,才能有效保障区域防洪安全。
