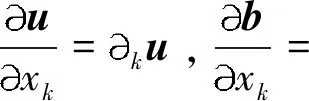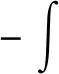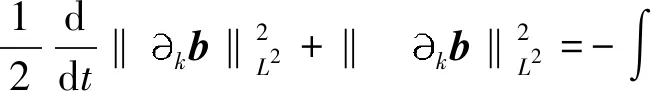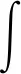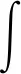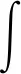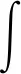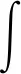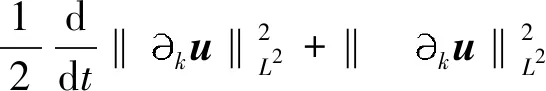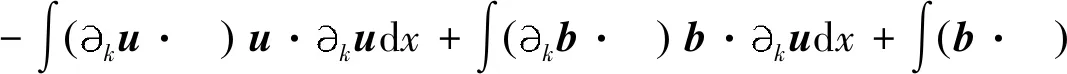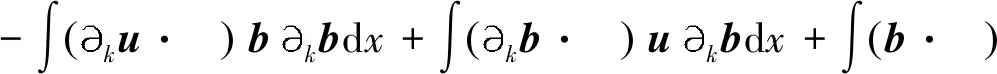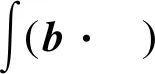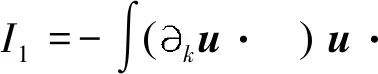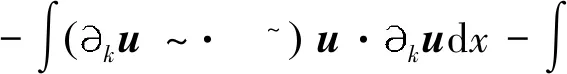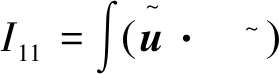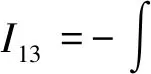三维MHD方程的正则性准则
2020-03-10付夕联
付夕联
(山东理工大学 数学与统计学院,山东 淄博 255049)
1 问题的提出
本文研究下面的三维不可压MHD方程
(1)
式中:u,b分别表示流速矢量和磁场矢量;p表示压力;v表示黏性系数;η表示磁扩散系数;u0和b0是给定的初始速度和初始磁场,并且·u0=·b0=0。如果v=η=0,式(1) 被称为理想MHD方程。
对于三维MHD方程弱解的正则性,文献[2-3]数值实验表明在解的正则性理论中速度场比磁场发挥着更重要的作用。近期这一事实得到了验证,何成等[4]获得了MHD方程由速度场u刻画的正则性准则
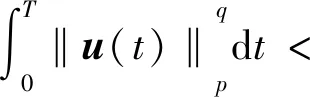
(2)
最近, Ji等[5]得到了下述结论:
并且
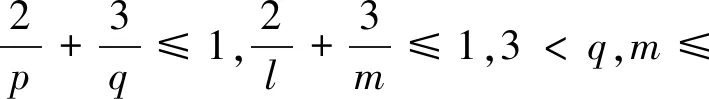
(3)
近期还有其他的关于三维 MHD方程正则性准则的刻画[6-7]。
定义1[1]三维 MHD方程的弱解(u,b)在[0,T)×H1(R3)是正则的,即(u,b)∈L(0,T;H1(R3))。
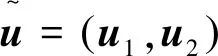
主要结论如下:
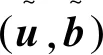

(4)
则(u,b)在[0,T]上是光滑的。
注记因为
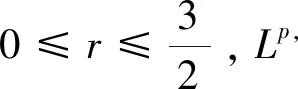
2 预备知识
首先,给出Morrey-Campanato空间的定义及性质,它在研究偏微分方程解的正则性中起着重要作用[8-11]。
定义2 对于1 容易验证 (5) (6) (7) 容易验证 (8) 引理2[12]对于0 (9) 式中C 仅依赖于r。 通过定义1,仅需证明(u,b)∈L(0,T;H1(R3))。因此,证明分为如下两步: 第一步L2估计 式(1)第一、二个方程分别与u,b作内积,并将所得到的方程分部积分,相加得 〈(-u·u+b·b),u〉+〈(-u·b+b·u),b〉=0 (10) 对式(10)关于0到T积分,有 (u,b)∈L 第二步H1估计 (11) (12) 则式 (11)及式(12)可化简为 (13) (14) 式(13)与式(14)相加得 (15) 首先将I1分解为如下两部分: (16) (17) 对于I12,同理可得 (18) 对于I13,类似于I11,由散度自由条件及分部积分公式,得 (19) 将式(17)—式(19) 代入式 (16), 得 同理,得 将I1—I4的估计代入式(15), 对k(1≤k≤3)求和, 得到 (20) 即得 (21) 由Gronwall不等式,得 u,b∈L([0,T);H1)∩L2([0,T);H2) 完成定理证明。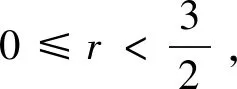
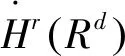
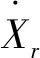
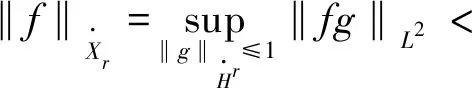
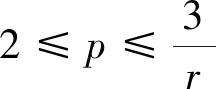
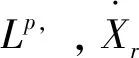
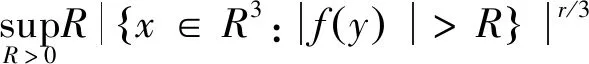
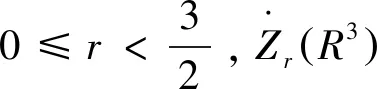
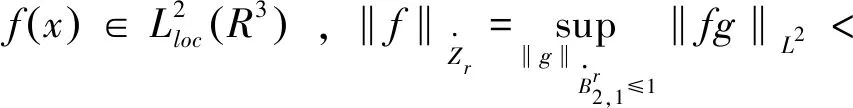
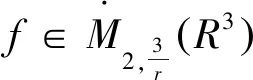
3 定理的证明