Microwave frequency downshift in the timevarying collision plasma
2020-03-09KunCHEN陈坤ChaoCHANG常超YongdongLI李永东HongguangWANG王洪广andChunliangLIU刘纯亮
Kun CHEN (陈坤), Chao CHANG (常超), Yongdong LI (李永东),Hongguang WANG (王洪广) and Chunliang LIU (刘纯亮)
1 Key Laboratory for Physical Electronics and Devices of the Ministry of Education, Xi’an Jiaotong University, Xi’an 710049, People’s Republic of China
2 School of Electronic Science and Engineering, Xi’an Jiaotong University, Xi’an 710049, People’s Republic of China
Abstract Microwave frequency downshift in the time-varying collision plasma has been demonstrated by particle-in-cell simulations. The simulation results are consistent with the theoretical analysis,and the preconditions for microwave frequency downshift are that the collision frequency needs to be greater than the incident wave frequency, and the plasma frequency is two times greater than the incident wave frequency.Finally,the simulation results are compared with the reported experimental results indicating good agreement.
Keywords:frequency downshift,time-varying collision plasma,particle-in-cell(PIC)simulation
1. Introduction
It is an old and active topic to study the interaction between the plasma and electromagnetic (EM) waves. As early as the beginning of the last century, the study of ionosphere and magnetosphere involved the propagation of EM waves in plasma [1, 2]. In the 2000s, the application of plasma stealth technology on aircraft was a hot topic at the time [3-7]. The use of plasma for the reflection, refraction, absorption and frequency conversion of EM waves, thereby achieves a plasma stealth effect, where the EM wave energy is attenuated.The phase angle of the EM wave is changed,and even the EM wave is diffracted. In addition, the ‘ionization blackout’has always been an area with continuing interest in aerospace research [8-11], which relates to the telemetry and GPS navigation disruption when the reentry vehicle travels at a supersonic velocity through the Earth’s atmosphere. This is due to the plasma sheath formed around the spacecraft by aerodynamic heating.The interaction between EM waves and plasma is also widely discussed in other fields,such as plasma diagnosis [12, 13], high power microwave atmospheric transmission [14, 15], fusion plasma reactors [16] and cyclotron wave (CW)-plasma ion sources for particle accelerators [17, 18].
As for the interaction between EM waves and the timevarying plasma, the frequency upshift is widely known. For example, a more perfect theoretical analysis is proposed by Kalluri [19, 20], the particle-in-cell (PIC) simulation verification is demonstrated by Chen[21,22],and several proofof-principle experiments are reported by Kuo [23] and Nishida [24, 25]. Nevertheless, the frequency downshift of EM waves in the time-varying collision plasma is disregarded. As early as 1994, the phenomenon of frequency downshift in rapidly ionizing plasma is presented by the experimental evidence [26]. A reasonable physical explanation is given by the fact that the phase velocity of EM waves in the time-varying plasma is reduced due to the electron collisions,the propagation constant k stays unchanged and the wave frequency decreases as the phase velocity decreases. In addition,frequency downshifts occur in the other complicated conditions, such as polarized waves in time-varying magnetized plasma [19], EM waves in periodic layers of the timevarying plasma [27, 28], and surface waves in the timevarying plasma layers [29].
In this paper, we further explore the impact of electron collisions on the frequency of EM waves, and it is also verified by PIC simulation. Microwave frequency downshift occurs in time-varying collision plasma under certain preconditions. For the research of microwave frequency downshift, it will greatly enrich the theoretical framework of the interaction between EM waves and plasma, and also provide a sound theoretical basis for the frequency conversion that may occur in the experiment. In addition, the regulation of the frequency upshift or downshift by controlling the propagation constant ( )β t and attenuation constant ( )α t of the EM wave are obtained by
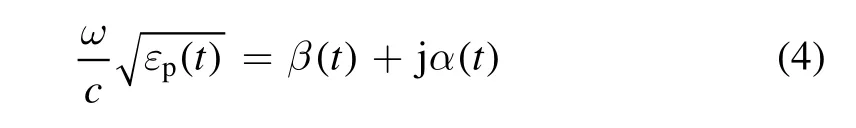
and

background gas pressure is realized, which suggests a potential application for devising a plasma switch.
From equations (1) and (5), the final frequency ( )ω t
fof EM waves in the time-varying is obtained by

The main content of this manuscript is organized as follows. In section 2, the problem description and theoretical analysis are given.In section 3,the PIC model is introduced in detail, and the PIC results consistent with the theory will be demonstrated. In section 4, combined with the reported experimental evidence, a reasonable explanation is given by PIC simulation and theoretical analysis.Finally,the conclusions are given and the potential applications are presented in section 5.
2. Problem description and theoretical analysis
When EM waves propagate in a time-varying plasma, the propagation constant k-conservation property can be used to show [16]where ( )ω t , andω0are the wave frequencies at time t and initial time, respectively, andn is the refractive index.

For a time-varying collision plasma, the equivalent dielectric coefficient is given by
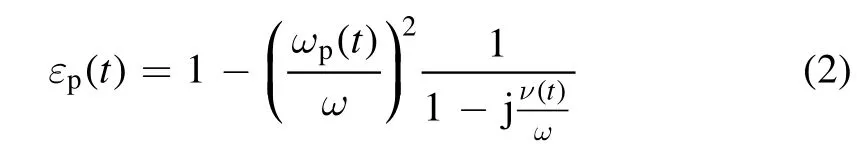
where ν ( t )is the collision frequency andω is the angular frequency of the wave in the plasma. The time-varying plasma frequencyis defined as

3. PIC simulation and results
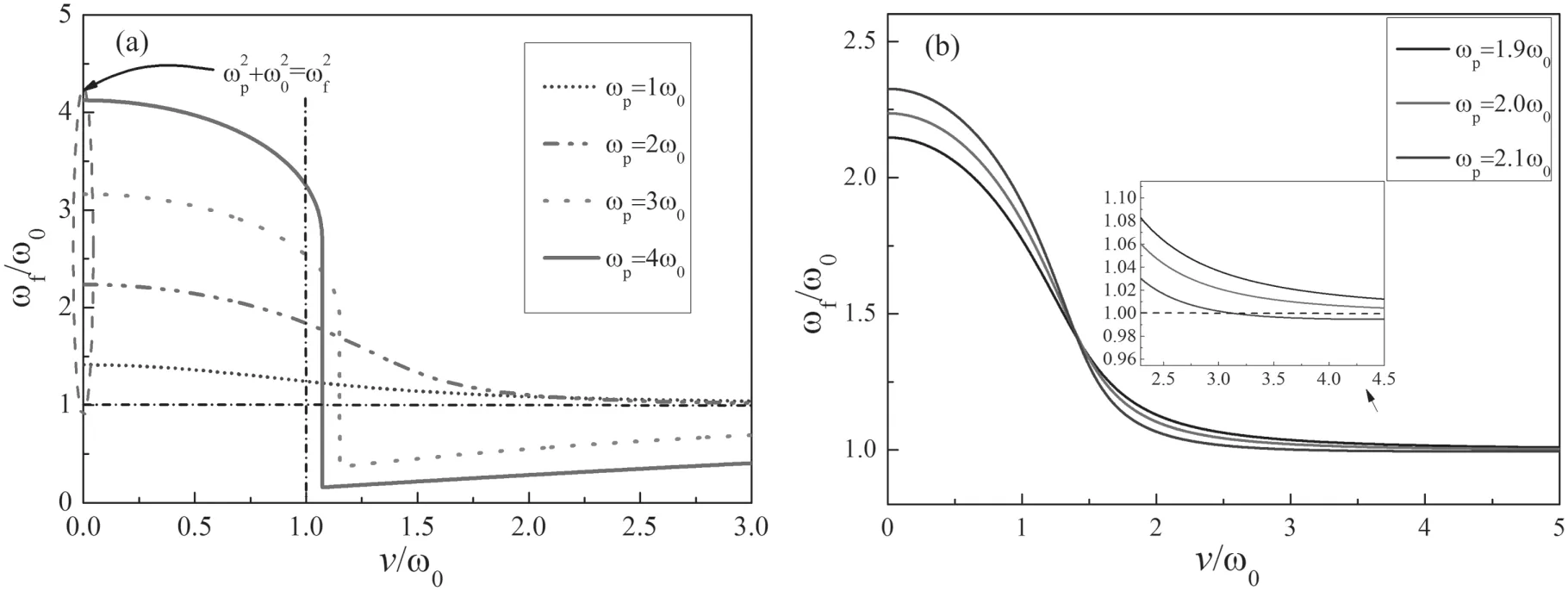
Figure 1.The relationship between the final frequency and the collision frequency with different plasma frequencies.
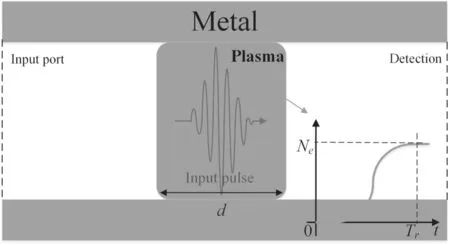
Figure 2.The schematic diagram in the PIC simulation (plasma density time domain distribution shown in bottom right corner).
A 2D PIC simulation in the software [30, 31] is established,and the schematic diagram is shown in figure 2. A uniform plane Gaussian pulse propagates into the region, where the plasma is suddenly created.During the ionization rise time ofthe plasma density is a time-varying process. In the PIC simulation, the dynamic plasma with time distribution is shown in figure 2. The plasma is evenly distributed in the spatial region and the density conforms to the tanh function distribution in time.For the setting of plasma thickness d,it is satisfied that the final EM wave withωfis still in the plasma region after the ionization rise time. Suppose that the plasma thickness d is too small, a part of wave propagates out the plasma region during the rise time, without undergoing a complete time-varying ionization process. At this time, the plasma thickness affects the frequency conversion. It will also increase our calculations when the plasma thickness is large enough.So it finds a balance between these two factors.Under this precondition, the plasma thickness d and the rise time Trhave no effect on the EM wave frequency [21, 22]. The collision frequency self-consistent process in the three models can refer to the MAGIC manual,in which the drag,scattering and straggling are modeled according to the following equations:


Here, the quantities⊥p1and⊥p2are the momentum components orthogonal to the incident particle motion,∣∣p is the incident momentum component. The drag model allows us to specify the coefficients for the electron neutral interaction. By default,the drag collision frequency is the Bethe slowing-down formula due to electron ionization, with ionization potential These two models generated from the Gaussian distribution sampling approximations, indicated with the〈〉-notation, and are valid in the limit of long path-length compared to the meanfree path. The scattering collision frequency is from the Moliere formula for multiple small-angles scattering by the shielded nucleus,and the straggling collision frequency is from the Vavilov treatment of the Landau distribution. These may all be expressed in the following form, based on a Bethe collision frequency,νBetheand a Coulomb logarithm,λ

where Z and ne=are respectively the charge number and electron number density of the target gas,Zincandβc are the charge number and relativistic momentum of the incident particle, respectively, andreis the classical electron radius. The bound-electron and screened-nucleus Coulomb logarithms, typically of values near 10, are

Figure 4.Experimental setup.
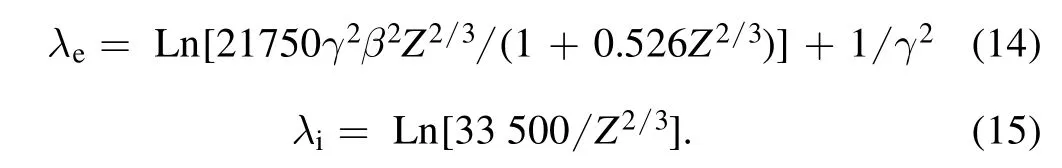
The simulation software used in this paper refers to the physical process in the MAGIC software. This momentum collision-frequency method considers the collision between various particles more comprehensively, close to the experimental results, and can be used to demonstrate the impact of collision frequency. At the weak ionization condition, the collision of electron-neutral particles dominates,that is to say,the drag model plays a major role. In the PIC simulation, we try to change the collision frequency by changing the air gas pressure P.The temperature is set to a constant value of 300 K.Due to the collision frequency proportional to the gas pressure,ν ~P,from the reported empirical formulas[32,33],the PIC results are shown in fgiure 3 which are basically the same as the results in figure 1. Near the pressure of 0.3 Torr, it is satisfied with the results of≈1.
4. Comparison with experimental results
As introduced above,frequency downshift in rapidly ionizing media has been observed in the experiment by Kuo S P and Ren A in 1994 [26]. Next, we will verify the theoretical analysis and the accuracy of the PIC results from the experimental results.Here,some main experimental parameters are given.The experimental setup is shown in figure 4.The timevarying self-generated plasma is created in a 0.6 m cube of plexiglas filled with dry air.The air pressure in the chamber isin the range of 0.2-1 Torr. The incident pulse with a central frequency of 3.27 GHz,is fed into the cube through an S-band microwave horn (H2) placed at one side of the chamber. A second S-band horn (H1) placed at the opposite side of the chamber is used to receive the transmitting pulse. The incident microwave power (PM) is generated by a single magnetron tube driven by a soft tube modulator. The modulator uses a pulse-forming network having a pulse width a pulse width of 1 ps and a repetition rate of 40 Hz.Microwave power of Pcis the breakdown threshold power of the background air.The spectra of the incident pulse and transmitting pulse are then compared. In table 1, it shows the main peak frequency spectra of the transmitted pulses for five different microwave power levels in the experiment.
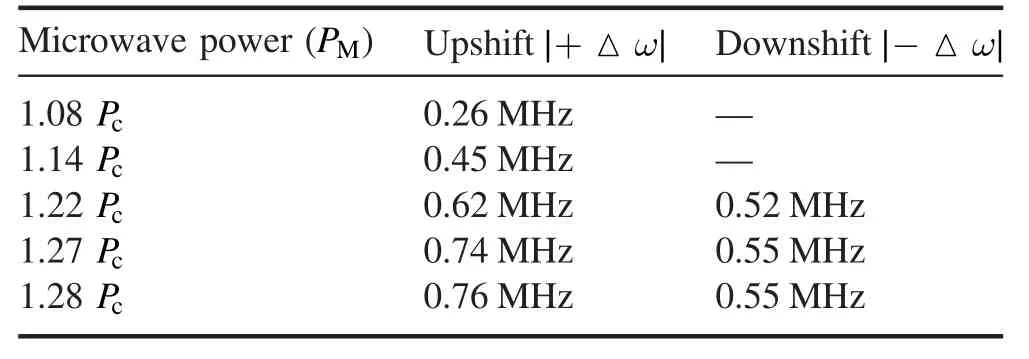
Table 1.The frequency spectra in the experiment with different incident power.

Figure 5.The schematic diagram of the impact of the ionization rise time on the spectra of the transmitted pulses with two clear peaks.

Figure 6.The frequency spectra of the final pulses with PIC simulation for different ionization rise time. Parameters:P0.4 Torr,2π =3.27 GHz,= and d =0.5 m.
5. Conclusion
In summary, we have demonstrated that the interaction between an EM wave and the time-varying collision plasma with PIC simulation. Combined with the reported experimental results, the reasonable explanation and the PIC simulation verification are given. Through further analysis, it is obtained that the downshift frequency only occurs in the time-varying collision plasma under the preconditions of>1and>2.It also gives a comprehensiveanalysis of the relationship among the frequency conversion,the plasma density and collision frequency. It enriches the theoretical knowledge of the interaction between electromagnetic waves and plasma, and provides a theoretical basis for solving the blackout problem and being applied to plasma stealth technology. In addition, based on theoretical analysis and PIC simulation, we have explained the experimental phenomena,which in turn verified the accuracy and reliability of our theoretical analysis.
Acknowledgments
The project is supported by National Natural Science Foundation of China (Nos. 51677145, 11622542 and U1537210).
猜你喜欢
杂志排行
Plasma Science and Technology的其它文章
- Analysis of the characteristics of the plasma of an RF driven ion source for a neutral beam injector
- Synthesis of vertical graphene nanowalls by cracking n-dodecane using RF inductivelycoupled plasma-enhanced chemical vapor deposition
- Application of persulfate in low-temperature atmospheric-pressure plasma jet for enhanced treatment of onychomycosis
- Magnetic field enhanced radio frequency ion source and its application for Siincorporation diamond-like carbon film preparation
- Comparison of Reynolds average Navier-Stokes turbulence models in numerical simulations of the DC arc plasma torch
- Effects of fast ions produced by ICRF heating on the pressure at EAST
