巧用数学方法实施生物学模型构建教学
2020-03-08左开俊
左开俊
摘要 根据中学阶段学生的认知范围,常构建的数学模型有图像模型、函数模型、多边形模型和几何模型等。设计和实施“数学模型构建”教学有助于实现教学样态的多样化、教学内容的跨学科、教学思想的统一化,使体现生物学科核心素养、科学思维、深度思考的学习和教学活动真正发生。
关键词 数学方法 生物学教学 模型构建教学
中图分类号 G633.91
文献标志码 B
文件编号:1003-7586(2020)08-0012-04
数学模型构建教学是以构建数学模型为载体,在生物学学科核心素养的指导下,通过符号、公式、图像等数学语言和数学工具,来定量描述生命系统发展状况的一种教学结构或教学程式。数学模型构建教学最大的特点就是:可以将日常中一个复杂的生物学问题借助数学模型的构建,最终转化成一个数学问题。《普通高中生物学课程标准(2017年版)》在“教学建议”中强调:教师应培养学生通过文字描述、数学表格、示意图、曲线图等方式完成报告,组织交流探究的过程和结果,并进行适当的评价。该段文字折射出来的数学方法思想,确立了数学模型构建教学在新课改中的地位,值得教师对此课题进行深入探讨和研究。
1构建数学模型实施生物学教学的常见类型
数学模型是联系数学知识与实际问题的桥梁,是数学知识在各个领域广泛应用的媒介,是数学科学技术转化的主要途径。教学过程中,通过数学模型构建的方式辅助解决生物学问题,能促进学生综合运用能力和综合分析能力的提高;同时,数学模型构建的方式也能使相关复杂的生物学问题变得简单直观和一目了然。
1.1图像模型构建——深入浅出简单直观,思维创造能力培養
图像模型就是将数与各种图形有机联合,实现彼此之间的数量关系。图像模型构建往往能使许多抽象的概念以及众多概念间的关系脉络分明地直观化、形象化呈现。这既有利于创造性思维的培育、探究性教学的实施;也有助于归纳与概括能力的培养、科学性解题思维的训练。教师若能经常考虑数图结合,则常会使教学方式别开生面,教学内容直观易懂。
【教学案例1】“密码子、反密码子、氨基酸”三者关系的教学。
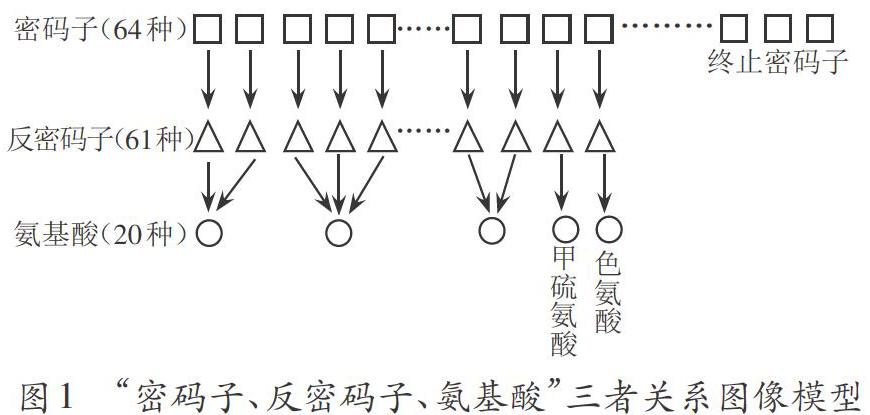
生物学教学中,最难教的就是多个知识点间的相互联系与区别。多个知识点间错综复杂的联系,常让学生找不到学习或解题的头绪。此时,若教师利用数图结合的图像模型,就会脉络分明地展现它们彼此间的相互关系和联系。例如,教师引导学生构建“密码子、反密码子、氨基酸”三者关系的图像模型(图1),教学效果就会事半功倍。
“密码子、反密码子、氨基酸”三者关系的图像模型概述:正方形代表密码子,有64种;三角形代表反密码子,有61种;圆形代表氨基酸,有20种。从图像模型中可以直观得出:①一种密码子只能与一种反密码子配对,但有三种密码子是终止密码子,没有与之配对的反密码子;②一种反密码子只能决定一种氨基酸,一种氨基酸却可以由好几种反密码子或密码子决定;③有两种氨基酸(甲硫氨酸和色氨酸)只能由一种反密码子或密码子决定。
运用图像模型构建教学的优点主要有:①深入浅出,简单直观。生物学教学过程中,有序地、深层次地向学生们讲清楚生物学问题的本质,是教学过程中的一个难点,也是一个重点。苍白的语言或文字描述,一方面常令一些关键词的地位不能重点呈现;另一方面大量的语言陈述也常令部分学生云里雾里、分辨不清。创建合理的图像模型,既能使复杂的问题简单化;又能使抽象的问题直观化。②思维创造,能力培养。构建图像模型是一种思维创造,其能通过形象、直观的数学元素,来提高学生对生物知识的加深与巩固,帮助学生培养和提高分析问题的能力、解决问题的能力。
1.2函数模型构建——概念铺展树立观念,辨识比对去伪存真
函数模型指对某个具体问题通过“建模”,转化成函数或方程式,进而解决问题的一种方法。运用到生物学中,就是将具体的生物问题,通过运用生物原理和数学方法将问题中所展示的概念性生物关系转化为相应的函数,然后利用数学知识和生物规则逐层铺展,以便寻求认知上的突破。
【教学案例2】“核苷酸种类、脱氧核苷酸和核糖核苷酸成分上异同点”的教学。
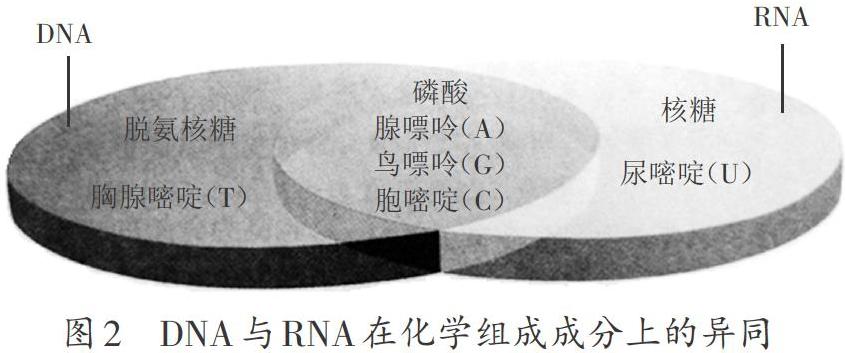
新教材在安排“核苷酸种类、脱氧核苷酸和核糖核苷酸成分上异同点”的教学内容时,建立了如图2所示的概念模型。该概念虽然能很清晰地解决了DNA与RNA在化学组成成分上的异同,但此概念模型未能涵盖此节的其他两个概念:①核苷酸的种类;②脱氧核苷酸和核糖核苷酸成分上的异同点。
如何通过模型的再构建,将众多概念直观、形象地整体展现呢?教师可以引入函数思想,通过构建函数模型,来开展此部分内容的教学。其教学过程为:(1)依据核苷酸分子组成,构建函数模型:把每个核苷酸分子看成是关于五碳糖和碱基这两个变量的二元一次函数,记作f(x,y)=x+y+P,其中X∈{核糖,脱氧核糖),y∈{A,G,C,T,U),P(磷酸)可看作是常数,同时当x=核糖时,y≠T,当x=脱氧核糖时,y≠U。
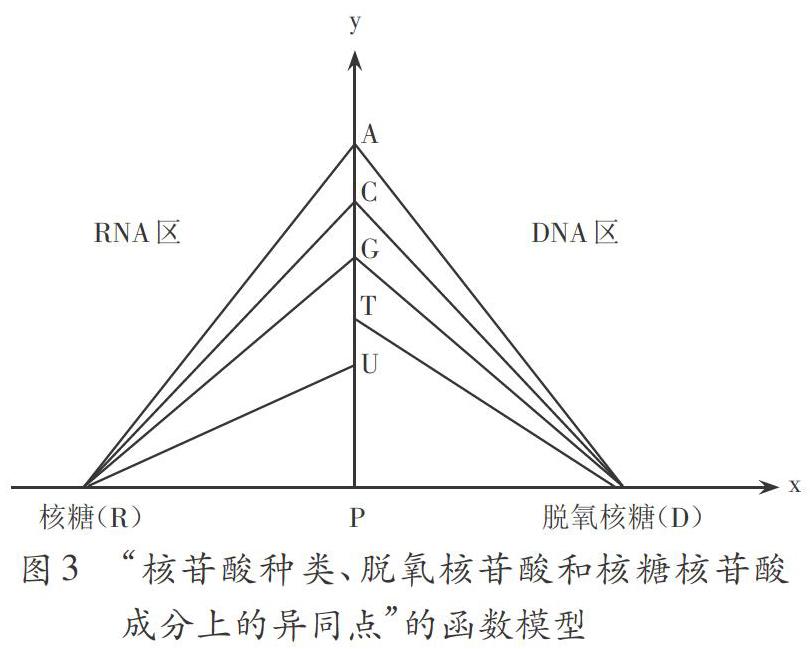
(2)画出函数模型:根据已设定的元素种类,构建函数模型(图3)。
(3)观察模型,得出相关结论:①核苷酸的种类:函数模型中,每个直角三角形分别代表一种核苷酸,第一象限为DNA区,含有4种脱氧核糖核苷酸,即APD、CDP、GDP和TDP四种;第二象限为RNA区,含有4种核糖核苷酸,即ARP、CRP、GRP和URP四种,故核苷酸的种类有8种。②脱氧核苷酸和核糖核苷酸在成分上异同点:根据X轴的正负方向,得出五碳糖的不同,即脱氧核苷酸的五碳糖是脱氧核糖,核糖核苷酸的五碳糖是核糖;根据Y轴正方向区域不同,得出脱氧核苷酸和核糖核苷酸共同的碱基是A、C、G,脱氧核苷酸特有的碱基是T,核糖核苷酸特有的碱基是U。
运用函数模型构建教学的优点主要有:①概念铺展,树立观念。函数模型能够依据重要概念的元素构成,直观而清晰地呈现各构成元素之间的异同点,能帮助学生形成正确的生物学重要概念,支撑众多概念的脉络化形成,帮助学生建立正确、科学的生物学观念。②辨识比对,去伪存真。学生通过对两个或多个概念之间直观地观察和比较,能迅速地找出其彼此间的联系和区别,消除了错误概念,建立科学概念;也培养了归纳与概括、分析与辨别的思维品质。
1.3多边形模型构建——融会贯通推理探究,他山之石可以攻玉
多边形是指由三条或三条以上的线段连接成的平面图形。在生物学教学中,构建多边形模型可以直观地解决多倍体复杂的减数分裂、受精作用、基因型及比例等问题。这一方面提供了一种避免大量假设与讨论的解决问题模式;另一方面也实现了将多维、复杂的问题在推理上可视化。
【教学案例3】“多倍体减数分裂产生配子的基因型及比例”的教学。
人教版高中教材《必修2·遗传与进化》中在介绍低温和一定浓度的秋水仙素处理萌发的种子或幼苗,能够引起细胞内染色体数目加倍的应用时,用常规教学方法来分析二倍体生物产生配子的基因型及比例,学生是可以理解的。但如果将二倍体拓展为多倍体生物体时,常规方法就显得非常杂乱和繁琐。如何解决“多倍体减数分裂产生配子的基因型及比例”的教学难题,可以通过构建多边形模型来进行诠释。
其教学过程为:(1)展现特殊案例,思考问题。以“基因型为Aa的番茄幼苗,经适宜浓度的秋水仙素处理后形成的四倍体”为案例,引导学生思考。在减数分裂时其形成配子的基因型及比例。(2)根据已有知识体系,进行推理:基因型为Aa的番茄二倍体,经适宜浓度的秋水仙素处理后,变成四倍体AAaa,这四个基因位于四条同源染色体上,在减数分裂形成配子的过程中,两两随机分到一极。③尝试构建四边形模型,解决问题:以基因型AAaa中的4个字母A、A、a、a为长方形的四个顶点。减数分裂的实质同源染色体的分离,就可以直观地表现为字母的两两结合,这样,就顺利且直观地在四边形模型上完成了三组连线(2条边长1组;2条宽1组,2条对角线1组),展现了四倍体减数分裂产生配子的基因型及比例的教学了(图4)。
(提示:如果是类似于AAa的三倍体,在构成四边形模型时,另一顶点可以用零替代。)运用多边形模型构建教学的优点主要有:①融会贯通,推理探究,能够运用学生掌握的多边形相关知识、证据和逻辑,对生物学议题进行构建、思考、展开论证,培养了学生创新学习和创新思维的能力。②依托多边形的几何知识(如四边形的2条边长、2条宽、2条对角线)为载体,引导学生将抽象、复杂的生物学行为问题,转化为形象、可演示的模型行为,体现了新教材的学科间联系的思想,培养了学生进阶认知的品质。
1.4几何模型构建——情境体验探寻发现,具身认知觅求真知
几何模型构建特指在生物教学中,通过创建相应的几何图形,并且根据其蕴含的相关知识(如定理、公理等),探寻和发现其与生物学问题之间的共性,达到直接解决问题的一种模式。
【教学案例4】“细胞为什么不能无限长大”的教学。
人教版高中教材《必修1·分子与细胞》在介绍细胞不能无限长大时,设计了一个“运用模型作解释”的思维训练,此训练中将细胞的形状设计成了一个正方体模型,该细胞模型的构建让学生们很难用肉眼从生活中找到其影子,一定程度上脱离了学生们的真实生活和认知范畴。笔者在施教此部分内容时,创设了一个真实的生活情境:现场给学生展示了一只熟鸡蛋,取出蛋黄交代清楚:未受精的蛋黄,实际上是一个卵细胞。接着,引导学生通过观察卵细胞,将细胞的形状构建成一个球体模型。教师将生物学问题转换成数学问题:卵细胞是通过什么结构从外界汲取营养物质的?汲取营养物质后,卵细胞的生长又是以何种形式呈现的?引导学生达成共识:卵细胞通过细胞膜从外界汲取营养,促进细胞体积的增长。顺势引入“表面积和体积的商”代表的含义为:单位时间内,卵细胞单位体积所摄入的营养物质的量,即卵细胞的生长速率。“表面积和体积的商”越大,卵细胞的生长速率就越快,反之则慢。通过以上的铺垫,此时就可以根据球体表面积、体积的数学公式,推导出细胞表面积和体积的关系为:细胞生长的速度=S/V=4JIR2/4/3JIR3=3/R。
学生观察关系式,发现矛盾:隨着卵细胞的生长,细胞的半径R随之增大,将其代入关系式就发现,此时细胞生长速率(S/V=3/R)却趋向于0。即单位时间内,卵细胞单位体积摄入的营养物质量为零时,细胞就可以无限制的长大。很显然,这个观点是错误的。学生通过推理,得出结论:细胞的表面积与体积的关系,是限制细胞不可能无限制长大的一种原因。
运用几何模型构建教学的优点主要有:①通过真实情境的体验,帮助和引导学生构建熟悉的几何模型(如案例4中的球体),利用学生们已贮存的相关知识(如案例4中的球体表面积和体积),尝试着去分析和解决生物问题,其有助于培养学生创新学习和创新思维的能力。②教师依托真实存在的生物为载体(例如本节中的蛋黄),培养学生善于从实践的层面探讨或尝试解决现实生活问题,帮助其树立生命观念,培养其勇于探索生命规律的品质。
2巧用数学方法实施模型构建教学的反思与体会
巧用数学知识实施模型构建教学,具有多方面的意义:①实现了教学样态的多样化。例如,应用于光合作用教学的曲线模型、应用于细胞分裂教学的柱状模型和折线模型、应用于遗传规律教学的集合模型和图像模型等,一方面为生物学教学的实施提供了多样化的手段,另一方面也为课堂教学注入了活泼的元素。②实现了教学内容的跨学科。生物学与数学知识的整合,其千变万化的构象,体现了课程标准强调的学科间的联系和渗透的要求。通过数学方法实施模型构建教学,加强了生物学与数学学科间的横向联系,为学生深层次地理解科学的本质、科学的思想方法和跨学科的科学概念和过程提供了借鉴。③实现了教学思想的统一化。生物学教学中融入数学方法,高度融入了新大纲的要求,如要培养学生学会用数字表格、示意图、曲线图等完成报告;能够将科学、技术、工程学和数学(STEM)知识和能力综合运用在实践活动中,解决生活中的实际问题。
巧用数学知识实施模型构建教学时,教师在构建模型的过程中,要多从学生的认知角度出发,多从学生的思维角度出发,多从学生贮备的数学知识出发,开发和探究出易于让学生接受的数学模型。教师在教学中,只有充分调动了学生的思维,并根据不同生物学问题的特点,引导学生进行有意义的数学模型建构,才能使数学模型内化于学生的头脑,成为他们分析和解决问题时心智操作的工具。
