建构一次函数助力调运决策

任蕾

一次函数在实际生活中有广泛的运用。学习了一次函数，我们可以运用一次函数知识建立数学模型解决实际问题。下面以调水问题为例，研究如何解决调运方案类问题。

例题 从A、B两水库向甲、乙两地调水，其中甲地需水15万吨，乙地需水13万吨，A、B两水库各可调出水14万吨。从A水库到甲地50千米，到乙地30千米;从B水库到甲地60千米，到乙地45千米。请你设计调运方案，使水的调运总量（万吨·千米）尽可能小。

【分析】题中变量较多，信息量大，可以把问题逐步分解：

（1）调运总量与哪些因素有关？

调运总量与水库（A或B）向需水地（甲或乙）供水的重量及调运路程有关。

（2）调运过程中包含哪些不同地点间的调运？路程各为多少？

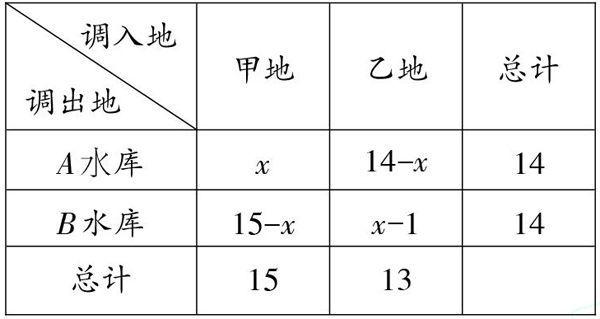
调运过程中有A到甲、A到乙、B到甲、B到乙这四种不同地点间的调运，路程分别为50千米、30千米、60千米、45千米。不难看出，两地之间的路程是一定的，结合（1）可知，调运总量随水库向需水地供水的重量的变化而变化。由此可以确定某水库向某需水地的供水量为自变量（不妨设从A水库调往甲地的水量为x万吨），通过列表厘清其他水库与各需水地调入的水量之间的关系，如下表：

（3）总的调运量由几部分组成？如何表示总的调运量？

由上图可知总的调运量由四部分组成，设总的调运量为y（万吨·千米），可列函数关系式：y=50x+30（14-x）+60.（15-x）+45 （x-1），化简为y=5x+1275。

（4）考虑自变量的取值范围。

要使每个量都有实际意义，即

（5）利用一次函数的性质，結合自变量的取值范围说出最佳调运方案。

本题中k=5>0，y随x的增大而增大。因此当x=1时，y有最小值，即调运量最小。最佳调水方案是：A水库向甲地调水1万吨，向乙地调水13万吨;B水库向甲地调水14万吨，向乙地调水0吨。

【归纳】解决含有多个变量的实际问题时，应先分析变量之间的关系，选取有代表性的变量作为自变量，进一步表示出其他变量，再根据条件寻求可以反映实际问题的数学模型（例如函数模型），建立相应的数学模型，利用相应的数学知识予以解决。

【练习】某市的C县和D县上个月发生水灾，急需救灾物资10吨和8吨。该市的A县和B县伸出援助之手，分别募集到救灾物资12吨和6吨，全部赠给C县和D县。已知A、B两县运送到C、D两县的每吨物资的运费如下表所示：

（1）设B县运到C县的救灾物资为x吨，求总运费w（元）关于x（t）的函数关系式，并指出x的取值范围;（2）求最低总运费，并说出总运费最低时的运送方案。

参考答案：

（1）w=-40x+980（0≤x≤6）。

（2）最低总运费为740元，运送方案为：B县运到C县的物资为6吨，B县运到D县的物资为0吨;A县运到C县的物资为4吨，A县运到D县的物资为8吨。