平面直角坐标系中含参数题的错因分析

姚月四

平面直角坐标系是初中阶段数学学习的重要内容之一，是后续学习函数等知识的重要基础。有些同学初学平面直角坐标系时，对含参数的习题常常无从下笔，出现一些典型错误。下面举几例，我们一起来分析。

一、基本概念不清

例1 在平面直角坐标系中，点P（m-3，2-m）不可能在（ ）。

A.第一象限 B.第二象限

C.第三象限 D.第四象限

【错解】B（或C、D）。

【错因分析】初看此题，横、纵坐标中都含有字母m，感觉无从下笔。其实，我们只要抓住各象限内点的坐标的符号特征：第一象限（+，+）、第二象限（-，+）、第三象限（-，-）、第四象限（+，-），分别列出不等式组分类讨论，即可求解。

【正确答案】A。

二、图形本质不明

例2 已知点M坐标为（2-a，3a+6），且M点到两坐标轴的距离相等，则点M的坐标是____。

【错解】（3，3）。

【错因分析】点M（x，y）到x轴的距离等于纵坐标的绝对值;点M（x，y）到y轴的距离等于横坐标的绝对值。若已知点到x轴、y轴的距离，求点的横纵坐标，则应考虑两解。

【正确答案】（3，3）、（6，-6）。

三、图形变换不熟

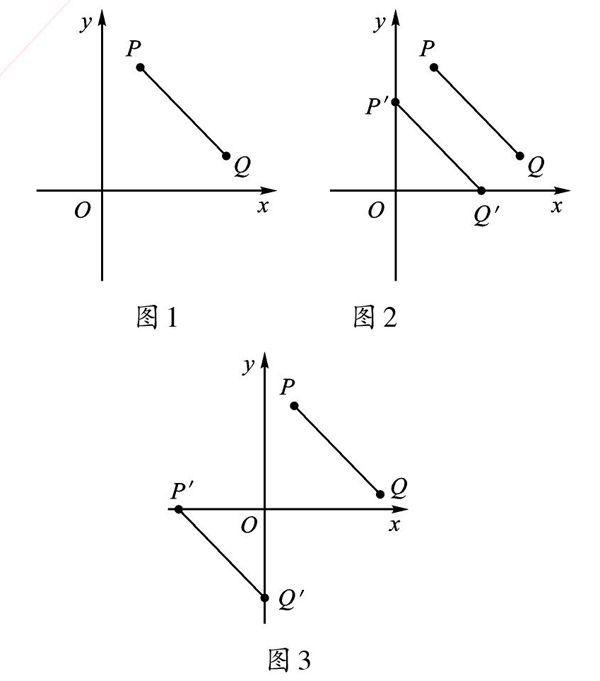
例3 如图1，第一象限内有两点P（m-3，n），Q（m，n-2），将线段PQ平移，使点P、Q分别落在两坐标轴上，则点P平移后的对应点的坐标是____。

【错解】（0，2）。

【错因分析】平移过程中点的坐标变化规律：右移横坐标加，左移横坐标减;上移纵坐标加，下移纵坐标减。图形的平移即为图形上点的平移，设平移后点P、Q的对应点分别是P′、Q′。分两种情况进行讨论：①如图2，P′在y轴上，Q′在x轴上;②如图3，P′在x轴上，Q′在y軸上。题目的条件既有数又有形，解决问题的方法也要既依托数也依托形，体现数形结合的思想。

【正确答案】（0，2）、（-3，0）。

同学们，通过对这三道题的错因分析，大家对解决含参数的平面直角坐标系有关问题有更深入的认识了吧？其实，在平时做题时，只要我们仔细审题，抓住图形或数量关系的本质特征，就一定能降低错误率！

挑战自我：已知点A（-2，-1），点B（a，b），直线AB与坐标轴平行且AB=3，则点B的坐标是____。

参考答案：（-2，2）、（-2，-4）、（1，-1）、（-5，-1）。

（作者单位：江苏省泰州市高港实验学校）