一题多解开阔思路

孙晋芳

很多时候我们能通过多种方法解决同一个问题，从而感知题中蕴含的数学思想。请看以下两例，一起感受“一题多解”的魅力。

例1 若点P（a，b）在第三象限，则点M（b-1，-a+l）在第____象限。

【分析】首先我们要掌握各象限内点横、纵坐标的特征，判断出a、b的正负情况，再根据对横、纵坐标的理解判断出点M的横坐标与纵坐标的正负情况，最后反过来根据各象限内点的坐标特征进行解答。

方法一：特殊值法

令a=-1，b=-1，则b-1=-2，-a+1=2，∴M（-2，2），

∴点M（b-1，-a+1）在第二象限。

方法二：抓住各象限内点的坐标特征

∵点P（a，b）在第三象限，

∴a<0，6<0，

∴6-1<0，-a+1>0，

∴点M（b-1，-a+1）在第二象限。

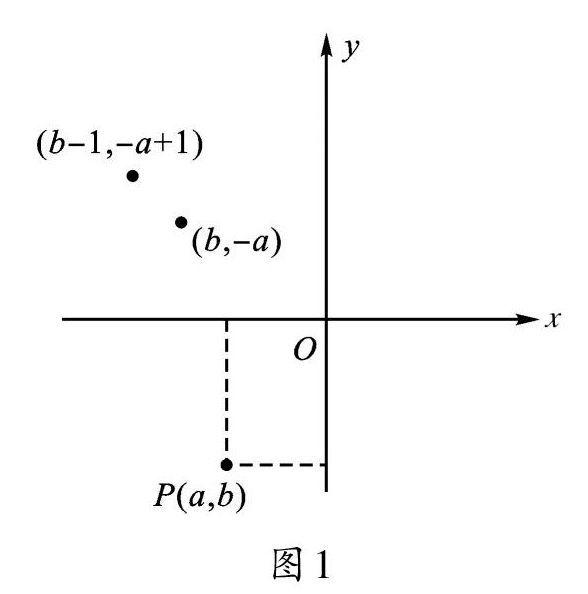
方法三：数形结合

∵如图1，点P（a，b）在第三象限，

∴a<0，b<0，

∴-a>0，b<0，

∴點（b，-a）在第二象限。

∴将点（b，-a）向左平移1个单位，向上平移1个单位，平移后的点仍在第二象限，∴点M（b-1，-a+1）在第二象限。

【点拨】本题考查了各象限内点的坐标的符号特征。记住各象限内点的坐标的符号是解决问题的关键，在此基础上可以给出不同的解题方法。

例2 已知：在平面直角坐标系中如图2，点A的纵坐标为4，AD⊥x轴，OA⊥AB，且OA=AB，求四边形OABC的面积。

【分析】此题的难点在于仅知道点A的纵坐标，即AD的长度，不能直接求出四边形OABC的面积，因此需要我们构造和转化。

方法一：如图3，过点A作AE⊥CB，垂足为E，这样根据条件可证得△ADO≌△AEB，易证四边形ADCE为正方形，那么四边形OABC的面积即为正方形ADCE的面积16。

方法二：如图4，过点B作BF⊥AD，垂足为F，这样根据条件可证得△ADO≌△BFA，所以S_{四边形OABC}=2S_△ADO+S_{长方形BFDC}=2×1/2 AD·OD+DC·DF

=AD·OD+AD·（AD-AF）

=AD·OD+AD·（AD-OD）

=AD²=16。

【点拨】本题考查了同学们对点的坐标的深度理解，若能将其与几何图形结合起来，通过割补法进行转化，将有限的条件运用起来，便能迎刃而解。

同学们应学会从不同角度、不同方位和不同的运算过程进行联想，以获取更多有益的知识，也可以将一些烦琐的甚至枯燥无味的习题变得充满趣味。