基于Pride岩石骨架模型的横波孔隙度计算方法*

李志愿

(中海石油(中国)有限公司天津分公司 天津 300459)

不同的岩石骨架模型分别从各自的角度建立了岩石骨架与岩石基质之间的关系。Nur等[1]通过定义临界孔隙度，认为岩石骨架的剪切模量与孔隙度之间存在线性关系。Pride等[2]则通过引入固结系数，认为岩石骨架的剪切模量与岩石孔隙度以及固结系数有关，而固结系数则取决于岩石所受到的有效压力和岩石的孔隙结构。之后，Lee[3]又对Pride模型进行了改进，本文将这两种理论统称为Pride模型。张佳佳 等[4]通过对不同岩石骨架模型的对比认为，相比于Nur模型，Pride模型对于中低孔隙度储层有更好的效果，适用性更广。

海上油田在勘探评价阶段，探井、评价井通常采用电缆测井系列，测井曲线齐全。但由于环境因素的影响，油田开发过程中，中子、密度测井的应用受到较大限制。声波测井因具有无放射源、节约钻时，并且能够获得纵、横波时差等优势，在开发井中的应用越来越广泛。声波测井不仅可以测量地层的纵波，也可以在软地层中进行偶极子波测量，获得质量较高的横波数据，从而为利用横波计算孔隙度提供了有利条件[5]。王建强 等[6]建立了基于Nur模型的横波时差孔隙度计算方法，但该方法在中低孔隙度储层并不适合。本文基于Pride岩石骨架模型，结合Biot-Gassmann理论以及岩石体积物理模型建立的横波孔隙度计算方法适用于中低孔隙度储层，适用范围更广，且应用效果更好。

1 理论分析与数学推导

在地震岩石物理中，Biot-Gassmann理论通常用来描述地震响应与岩石物性之间的关系，但是该理论并没有阐述岩石骨架和岩石基质之间的关系。为了能够有效地建立二者之间的关系，出现了各种各样的岩石骨架模型，如Nur模型和Pride模型等，分别从不同的角度阐述了多孔岩石的骨架与基质之间的关系。岩石骨架模型的出现使得声波与储层物性、岩石骨架及岩石基质之间建立起了联系，为利用横波计算孔隙度提供了理论基础。同时，相比于纵波时差，横波时差受流体的影响更小，每单位孔隙度变化引起的横波时差变化也比纵波时差变化大，横波时差对孔隙度的反映更灵敏[7]，因此利用横波计算孔隙度是可行的，且具有一定的优势。

2004年Pride等[2]提出干岩石的剪切模量与骨架的剪切模量具有以下关系：

(1)

式(1)中：μd为干岩石的剪切模量，MPa；μma为骨架的剪切模量，MPa；φ为孔隙度，f；α为固结系数，无量纲，表示岩石孔隙结构的复杂程度，对于砂岩通常取2<α<20。等效介质理论指出固结系数α取决于岩石的孔隙结构和岩石骨架的剪切模量与体积模量之比。式(1)中常数1.5可以为2或者5/3，该因子选取的目的主要是为了在利用Pride岩石骨架模型反演横波时差时，有较为精确的纵横波速度比。为了避免式(1)中因子1.5选取的任意性，Lee[3]针对Pride模型的剪切模量公式做了进一步改进：

(2)

其中

(3)

Biot-Gassmann理论认为孔隙流体不改变饱和岩石的剪切模量，即岩石骨架的剪切模量等于饱和流体岩石的剪切模量[8-9]

μ=μd

(4)

式(4)中：μ为饱和流体岩石的剪切模量，MPa。

依据剪切模量与密度、横波速度之间的关系，饱和流体岩石的剪切模量和骨架的剪切模量分别为

(5)

(6)

式(5)(6)中：ρ为饱和流体岩石的密度，kg/m3；Vs为饱和流体岩石的横波速度，m/s；ρma为岩石骨架的密度，kg/m3；Vs,ma为岩石骨架的横波速度，m/s。

因此,由式(2)～(6)可以得到

(7)

对于饱和流体泥质砂岩，其岩石体积物理模型为

ρ=(1-φ-Vsh)ρma+Vshρsh+φρf

(8)

式(8)中：Vsh为泥质含量，f；ρf为流体密度，kg/m3；ρsh为泥岩的密度，kg/m3。

横波速度与横波时差之间存在如下关系：

(9)

(10)

式(9)、(10)中：Δts为饱和流体岩石的横波时差，s/m；Δts,ma为岩石骨架的横波时差，s/m。

将式(8)～(10)代入式(7)整理后可得：

(11)

以Pride岩石骨架模型为基础，结合Biot-Gassmann理论与岩石体积物理模型，式(11)最终建立了泥质砂岩储层横波时差与储层孔隙度之间的关系。式(11)中的泥质含量Vsh可以通过测井曲线计算得到较为准确的数据，各种密度参数ρma、ρsh和ρf可根据油田实际选取。因此，如果得到岩石的骨架横波时差Δts,ma和固结系数α就可以采用横波时差利用式(11)计算储层的孔隙度。所以，能否准确地求取固结系数和骨架横波时差是利用该方法计算横波孔隙度的关键。

2 参数确定方法

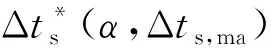
(12)

达到最小[10-11]，此时得到的骨架横波时差Δts,ma和固结系数α即认为是岩石的骨架横波时差和固结系数。

研究区渤中3油田东营组储层为辫状河三角洲沉积，砂体横向展布稳定，砂体连片发育，单砂体厚度2.0～26.9 m，平均16.2 m，储层岩性以中、细粒岩屑长石砂岩为主，矿物成分主要为石英、长石、岩屑，孔隙度范围为16.4%～22.0%，平均为19.4%，为中孔隙度储层。孔隙主要发育粒间孔，连通性较好，粒间充填矿物主要为伊利石、高岭石。选取该油田取心探井BZ3-1井作为关键井，利用该井的伽马曲线计算泥质含量，中子、密度曲线交会计算孔隙度，在此基础上利用式(11)与式(12)进行骨架横波时差和固结系数反演。图1为关键井BZ3-1井利用孔隙度、泥质含量以及横波时差反演的岩石骨架横波时差和固结系数图。图中第6道和第7道分别为测井计算的泥质含量和中子、密度曲线交会计算的孔隙度与岩心分析数据的对比，可见二者计算的精度均较高，可以用于后续参数的反演；第9道为实测的横波时差与反演的横波时差之间的对比。在反演开始时，先分别给骨架横波时差和固结系数赋初值，然后通过不断地优化骨架横波时差值和固结系数值，使得式(12)达到最小值，即实测的横波时差与反演的横波时差几乎重叠，说明反演效果满足要求，反演得到的骨架横波时差和固结系数可以进行后续参数的拟合；第10道为最优化反演得到的骨架横波时差，在储层段(研究区泥质含量的有效厚度下限为0.2)骨架的横波时差值在355 μs/m左右，在非储层段随着泥质含量的增加骨架的横波时差值明显增大；第11道为最优化计算的固结系数，固结系数随着泥质含量的增加存在明显增大的现象。

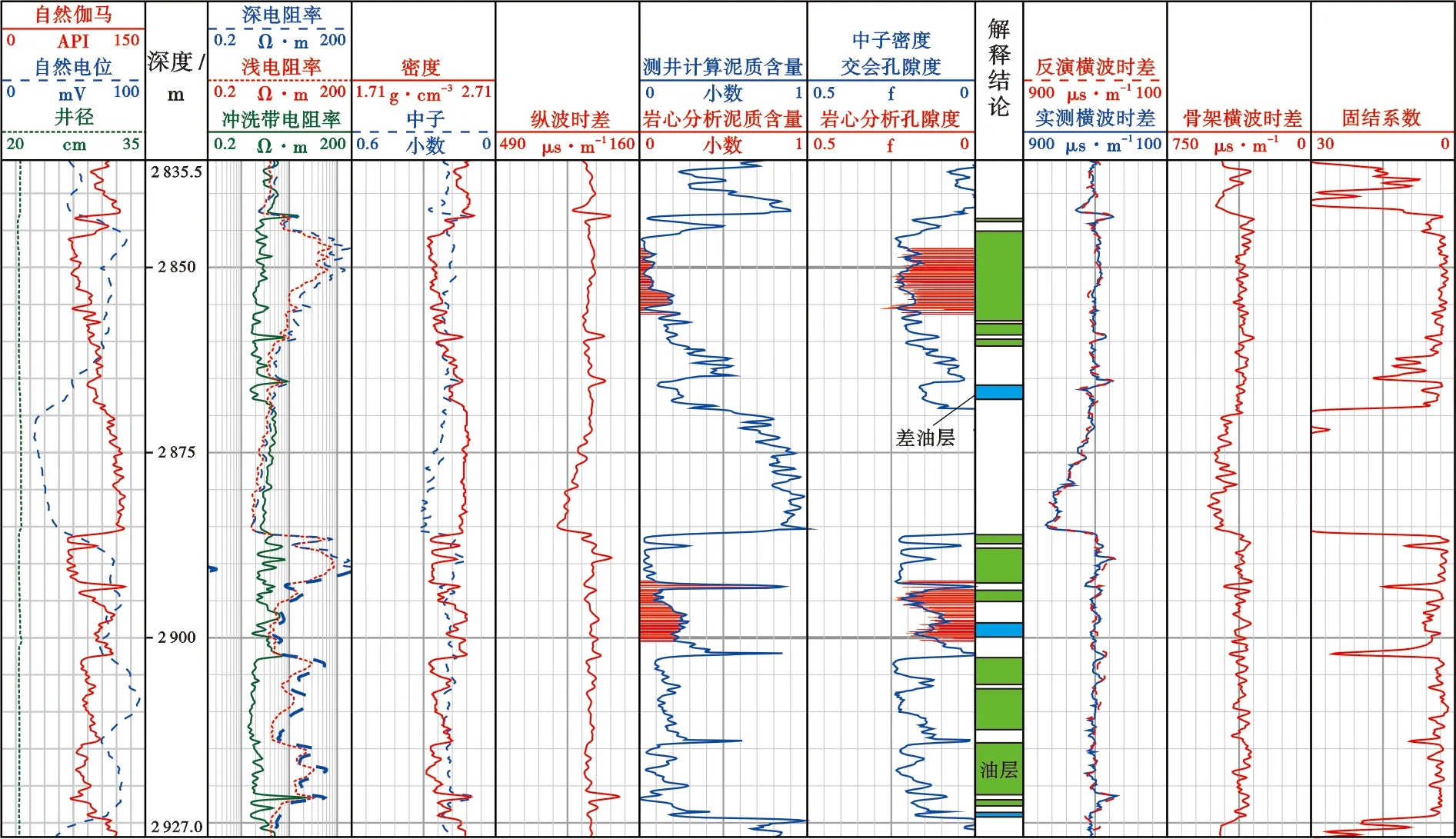
图1 渤中3油田关键井BZ3-1井横波孔隙度参数反演结果

在同一稳定分布的砂体中，黏土的矿物类型及分布形式是相对稳定的[12-13]。图2为关键井BZ3-1与开发井BZ3-A井的黏土矿物扫描电镜特征。该图表明关键井与开发井储层孔隙中充填的均为书页状高岭石和丝片状伊利石，黏土矿物的分布形式也较为一致。表1为关键井BZ3-1与开发井BZ3-A井东营组储层的黏土矿物相对含量的对比。可见该油田关键井和开发井储层中黏土矿物均以高岭石为主，其次为伊利石和伊蒙混层，仅含少量绿泥石。因此，对于研究区来说，黏土的矿物类型和分布形式是较为稳定的，方法中涉及的骨架横波时差和固结系数可以认为主要与泥质含量多少有关。

图2 渤中3油田关键井BZ3-1井与开发井BZ3-A井黏土矿物扫描电镜特征

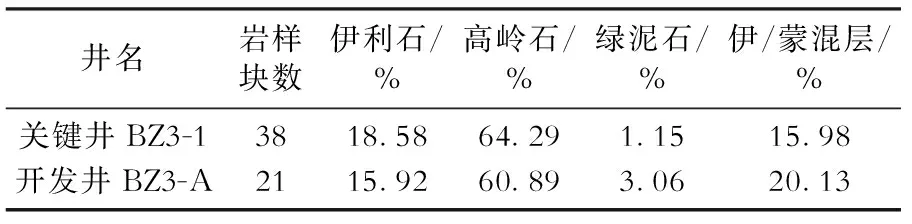
表1 渤中3油田关键井BZ3-1井与开发井BZ3-A井黏土矿物相对含量对比

在关键井BZ3-1井中选取稳定发育的砂岩段和泥岩段，分别利用泥质含量建立骨架横波时差和固结系数的计算公式，并将其应用到采用声波测井的开发井中，从而能够利用式(11)计算横波孔隙度。图3为岩石的骨架横波时差与泥质含量的关系，图4为固结系数与泥质含量的相关性。由两图可见，二者与泥质含量均具有较好的相关性。拟合得到的公式分别如下：

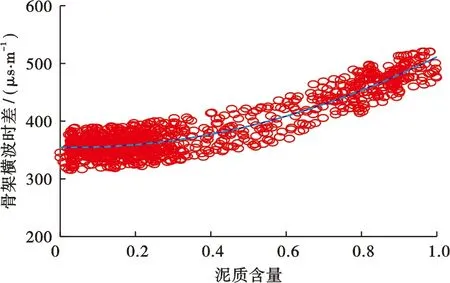
图3 渤中3油田关键井BZ3-1井骨架横波时差与泥质含量关系

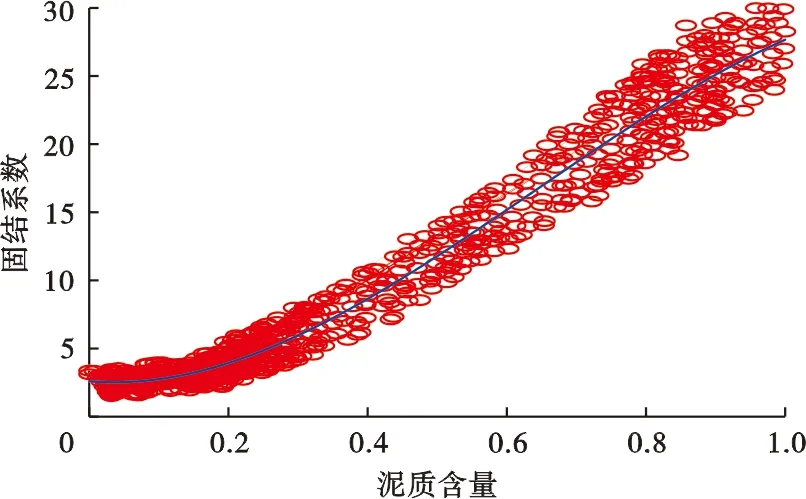
图4 渤中3油田关键井BZ3-1井固结系数与泥质含量关系

骨架横波时差

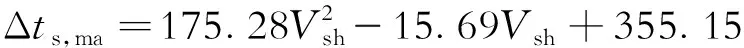
(13)

固结系数

(14)

3 应用效果分析

渤中3油田开发井BZ3-A井在实施过程中孔隙度测井采用过套管声波测井，未进行中子和密度测井。将利用BZ3-1井建立的骨架横波时差和固结系数的计算公式应用于该井中，采用Pride岩石骨架模型计算横波孔隙度。图5为该井测井曲线及横波孔隙度处理结果。第11道为采用Pride岩石骨架模型计算的横波孔隙度和采用威里平均时间公式计算的纵波孔隙度与岩心分析孔隙度的对比。

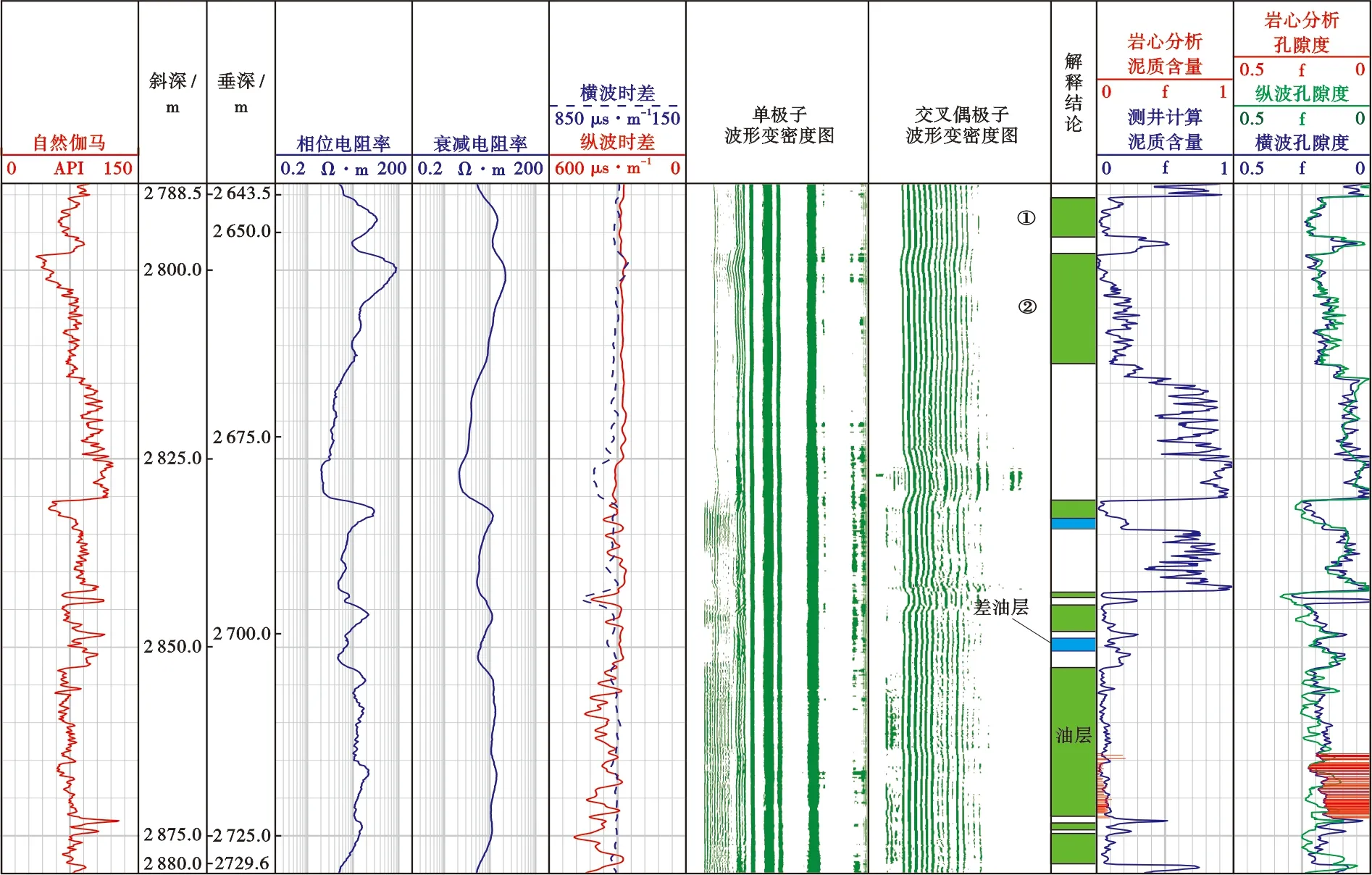
图5 渤中3油田开发井BZ3-A井横波孔隙度处理结果

BZ3-A井在斜深2 788～2 830 m井段固井质量较好，过套管声波测井获得的单极子波形(第7道)和偶极子波形(第8道)质量均较高，从而能够提取可靠的纵、横波数据。由图5可知，在斜深2 788～2 830 m井段横波孔隙度与纵波孔隙度对应较好，图中油层①测井计算的横波孔隙度为20.1%，纵波孔隙度为20.3%，油层②测井计算的横波孔隙度为17.8%，纵波孔隙度为16.9%,两层分别采用两种方法计算的孔隙度均比较接近，都能够较为真实地反映储层物性。在斜深2 830～2 880 m井段固井质量较差，由于交叉偶极声源工作频率为低频，低频声源产生的能量穿透性较强，而单极子声源工作频率较高，相对来说穿透性较差，受附近井眼状况影响较大；同时横波测量的是挠曲波(非对称波)，当固井质量不好时，套管与地层之间通常为非均匀环境，相比于单极子接收器，偶极子接收器对于非对称波更敏感，对接收挠曲波信号相对有利。因此，在2 830～2 880 m井段单极子波形中由于包含套管波信息(第5道左侧变密度显示区域)，使得提取的纵波时差受到套管波的影响，出现明显的异常现象，而偶极子波形质量较高，从而能够准确地提取地层的横波。从第11道该井段两种孔隙度与岩心分析孔隙度对比可知，横波孔隙度与岩心分析孔隙度较为吻合，纵波孔隙度则由于波形质量的问题与岩心分析孔隙度差别较大。表2为取心井段(2 864～2 873 m)横波孔隙度和纵波孔隙度与岩心分析孔隙度的对比，从表中可以看出，在取心井段，采用横波计算的孔隙度与岩心分析孔隙度较为接近，而纵波孔隙度则与岩心分析孔隙度差别较大。采用本文方法计算的横波孔隙度精度更高，为孔隙度计算提供了一种有效的方法。

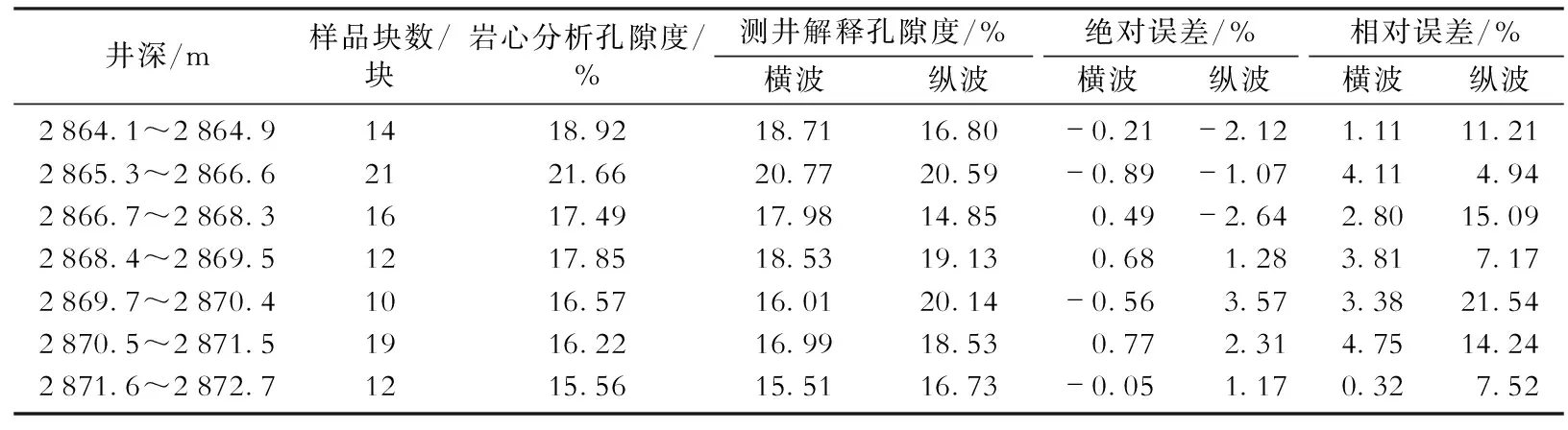
表2 渤中3油田开发井BZ3-A井横波孔隙度、纵波孔隙度与岩心分析孔隙度对比表

4 结论

1) Pride岩石骨架模型建立了岩石骨架与岩石基质之间的关系，且适用于中低孔隙度储层。通过该模型结合Biot-Gassmann理论以及岩石体积物理模型，建立了泥质砂岩储层横波时差与储层孔隙度之间的关系，通过该关系进而可以利用横波时差计算储层孔隙度。

2) 对于Pride岩石骨架模型中涉及的骨架横波时差和固结系数2个参数，提出了最优化的反演方法，并利用测井参数拟合得到2个参数的计算公式，为方法的进一步推广应用奠定了基础。

3) 在同一稳定展布的砂体中泥质的矿物类型及分布形式相对稳定的假设下，将建立的基于Pride岩石骨架模型的横波孔隙度计算方法应用于研究区开发井中，取得了较好的实际应用效果。