线性脉冲微分方程Runge-Kutta方法的稳定性*
2020-03-08张雨婷李洪雨刘雨欣龚王微
张 玲,毕 晴,张雨婷,李洪雨,刘雨欣, 龚王微
(大庆师范学院)
0 引言
脉冲微分方程(IDES)被广泛应用于许多科学技术领域:如物理、力学、种群动力学、药物学、脉冲技术、工业机器人技术,化学技术,生物技术,经济学等. 尤其是脉冲微分方程(IDE)的精确解稳定性已经得到了广泛的研究,但是许多IDE不能用解析方法求解,求解方法也较复杂.因此,数值方法是一个很好的选择. 近年来IDE数值方法的稳定性得到了广泛的研究. 文献[1-6]给出了脉冲微分方程精确解的稳定性,而文献[7-11]给出了脉冲微分方程数值解的稳定性.
众所周知,李普希茨条件不可能保证常微分方程的稳定性.然而该文研究了线性的IDE的精确解和数值解在李普希茨条件下的渐近稳定性:
(1)
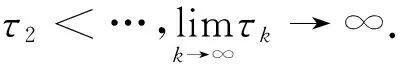
定义1 函数x:[t0,∞]→Ck是(1)的解,如果

(2)对于t∈(t0,+∞),t≠τk,k=1,2,…,x(t) 是可微的并且x′(t)=αx(t).
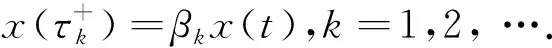
1 精确解的渐近稳定性
在该节中,研究(1)的精确解的渐近稳定性.为了研究x(t) 的整体稳定性,考虑另一个初始数据的方程(1):
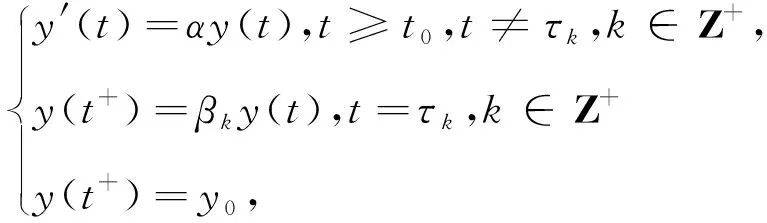
(2)
其中z+={1,2,…}
定义2[1,5]方程(1)的精确解x(t)是
(1)稳定的,如果对于任意的ε>0,存在一个正数δ=δ(ε),对于(2)的任何解y(t),当‖x0-y0‖<δ时,有‖x(t)-y(t)‖<ε,
∀t>t0.
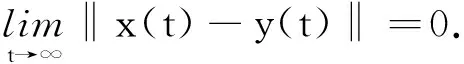
定理1 假设存在一个正的常数γ,使得
τk-τk+1≤γ,k∈Z+. 如果有一个正常数C, 对于任意的k∈Z+.使得
βk·eα(τk-τk-1)≤C<1
则(1)的精确解是渐近稳定的.
证明任意t∈(τk,τk+1],k=0,1,2,…
得到
由Gronwall定理,任意t∈(τk,τk+1],
k=0,1,2,…有

由定义1(3)有
从而
因此,根据条件(3)和(5),对于任意t∈(τk,τk+1],k=0,1,2,…得
‖x(t)-y(t)‖≤‖x0-y0‖β1eα(τ1-τ0)·β2eα(τ2-τ1)…βk·eα(τk-τk-1)·eα(1-τk)≤‖x0-y0‖·Ckeαy
进而
‖x(τk+1)-y(τk+1)‖≤‖x0-y0‖·Ckeαy
和
因而,对于任意ε>0,存在δ=e-αyε, 当‖x0-y0‖<δ时,
‖x(t)-y(t)‖≤‖x0-y0‖·Ckeαy≤‖x0-y0‖eαy<ε
对于任意t∈(τk,τk+1]k=0,1,2,…,
‖x(t)-y(t)‖<ε,∀t>t0
因此,方程(1)精确解是稳定的. 显然,对于任意t∈(τk,τk+1]k=0,1,2,…
‖x(t)-y(t)‖≤‖x0-y0‖·Ckeαy→0,k→∞.
同样,得
‖x(τk+1)-y(τk+1)‖≤‖x0-y0‖·Ckeαy→0,k→∞
和
因此,方程(1)的精确解是渐近稳定的.
2 显式的Kunge-Kutta方法
在该节中,给出方程(1)当p=4时p阶p级显式Runge-Kutta方法的渐近稳定性. 方程(1)Runge-kutta方法可以构造如下:
(3)
方程(2)的显式Runge-kutta方法:
(4)

tk、1+cihk的地方,有k∈N={0,1,2,…}.
l=0,1,…,m-1,i=1,2,…,s

定义3 对脉冲微分方程(1)的显式龙格库塔方法(3)是
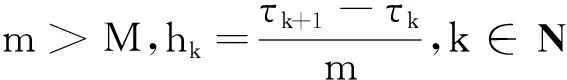
存在一个正数δ=δ(ε).当‖x0-y0‖<δ,使得‖xk-yk‖<ε,∀k∈N.
其中xk=(xk,0,xk,1,…,xk,m)和yk=(yk,0,yk,1,…,yk,m)
(2)渐近稳定的.如果它是稳定的
∃M1>0,对于任何的m>M,
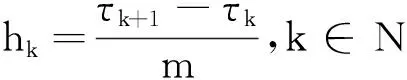
考虑(1)的4阶段显式龙格-库塔方法:
(5)
和
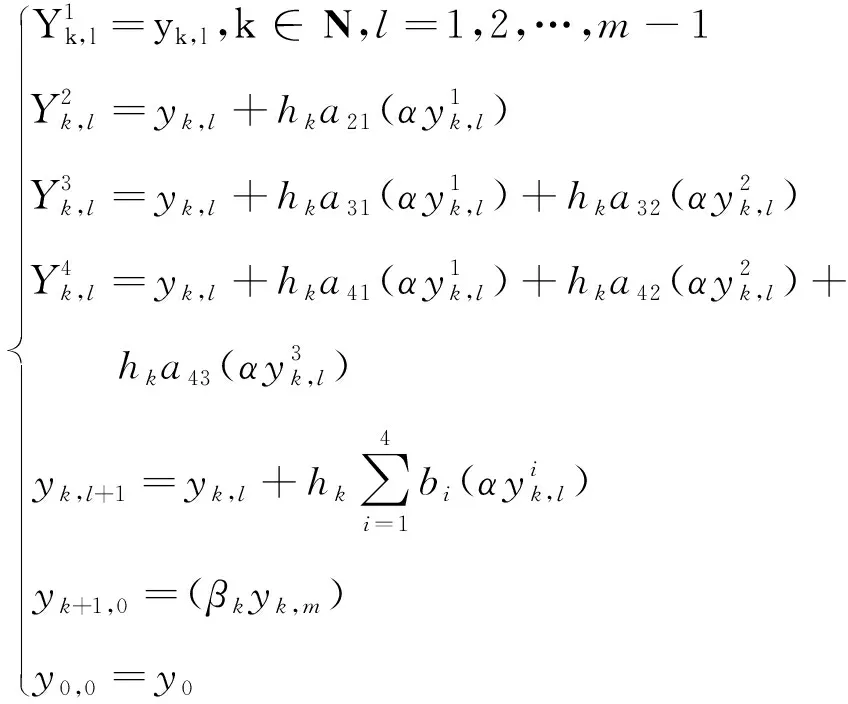
(6)
定理2 假设显式龙格-库塔方法(5)的所有系数都是非负的(ai,j≥0,bi≥0,1≤i≤4)和
(7)

(8)

(9)


类似的,可以得到
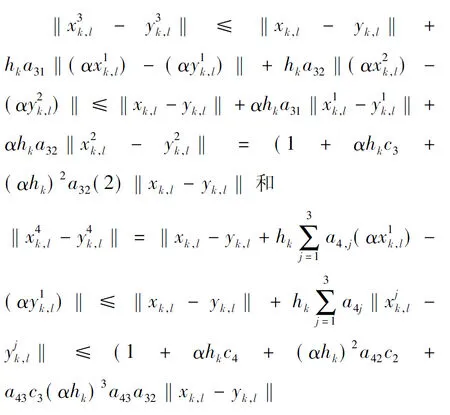
上述三个不等式可以得到:
因此对任意的k=0,1,…,m,有
‖xk,l-yk,l‖≤‖xk,0-yk,0‖·eαhk
由条件(3),可以得到:
‖xk,l-yk,l‖≤‖x0-y0‖·(β1·eα(τ1-τ0))·(β2·eα(τ2-τ1))…(βk·eα(τk-τk-1)eαhk)≤‖x0-y0‖·ckeαy
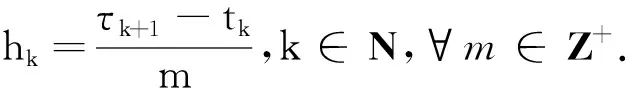
3 数值实验
在该节中,给出了简单的数值例子.
例1 考虑以下简单的标量IDE
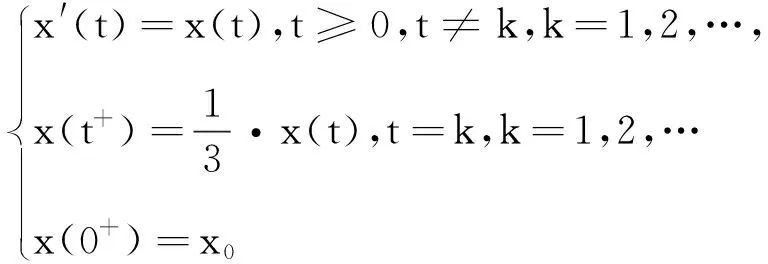
(10)
和
(11)

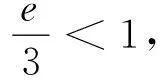
(11)的精确解满足
因此
显然(10)和(11)的精确解都是渐近稳定的.
4 结论与未来工作