纵向倾斜状态下的狙击步枪射击偏差校准方法*
2020-03-07原沙沙刘甜甜
苏 胜,原沙沙,刘甜甜
(西安工业大学 艺术与传媒学院,西安 710032)
狙击步枪在纵向倾斜状态下射击会出现一定的偏差,我国狙击步枪在设计方面参考苏联SVD型狙击步枪进行测绘并仿制,定型79式狙击步枪,精度相对西方国家处于中下水平[1-3],在此之前我国对狙击步枪并没有准确的概念。文献[4]表明我国开始研制专用狙击步枪弹,依据狙击弹来匹配设计枪械,采用弹头前装成型工艺,大幅度提高了弹丸加工的一致性和轴对称性,有效解决了枪口扰动问题。通过改变弹头的设计,最大限度控制弹头飞行中偏离轴心线的幅度,从而保证了射击精度。文献[5]运用卡尔曼预测滤波对脱靶量滞后进行补偿,得出瞄准线偏差,将陀螺数据滤波后积分得出另一瞄准线偏差,根据加权融合算法,得到加权融合后瞄准线偏差。文献[6]通过建立反坦克火箭筒的坐标系,描述反坦克火箭筒横倾前后的筒身状态,通过分析和坐标变换,得出横倾状态下射击偏差量的数学模型。利用Origin软件,计算使用典型弹种射击时,反坦克火箭筒在不同距离、不同横倾角度下的方向和高低偏差量。文献[7]针对某狙击步枪射击精度不达标的问题,采用正交试验法改进某狙击步枪的射击精度。在研究中表明,现有技术只是对狙击枪射击枪口瞄准镜的偏差进行了分析,并未对狙击步枪在纵向倾斜状态下射击偏差进行定量测算。
本文利用Matlab软件建立倾角偏差量计算模型来测算狙击步枪纵向倾斜状态下射击引起的枪弹方向以及表尺变量差,以模拟的实际导弹轨迹导出的数据为准,结合子弹在理想条件下的射击轨迹做比较,为狙击手提供有效的参考数据。以横倾状态下射击的火箭弹方向及表尺偏差量[7]计算结果为基础,分析火控采用该种修正方法的原因并以测算的结果作为基础数据,为狙击步枪射击的精确程度做有效的参考。
1 弹道轨迹模型的建立
实际情况下,狙击步枪子弹射出枪膛后的运功轨迹是抛物线,在运动过程与空气的摩擦受到阻力,同时受到天气条件、气流、空气密度等条件的影响,本文假设实验的条件:① 在无风、普通大气环境下空气密度一定;② 不考虑子弹在运行过程中产生的微小形变;③ 重力加速度(g=9.81 m·s-2)并且始终向下;④ 不考虑地球自转产生的科氏加速度[8-9]。实际射击中子弹在发射的过程中阻力因素不可忽略,因此要考虑空气密度以及阻力因素,可通过Matlab软件进行设定模拟弹道运动轨迹。
1.1 枪身直角坐标系
根据狙击步枪的使用状态建立直角坐标系,描述狙击步枪纵向倾斜状态下的枪身状态,狙击步枪是以八字架的轴心作为固定的支撑点,居于战场置高点,通过八角架支撑点进行枪身的高低调节和方向旋转,因此将支撑点作为整个坐标系的原点位置,依据狙击枪枪身的状态来建立坐标系以o-xy表示,o作为狙击步枪旋转时的轴心点(原点),为枪身轴线和三脚架固定器的旋转交点,x轴作为狙击枪纵向倾斜状态下水平面上的投影,y轴为垂直向上方向,图1为狙击步枪枪身平面直角坐标系。
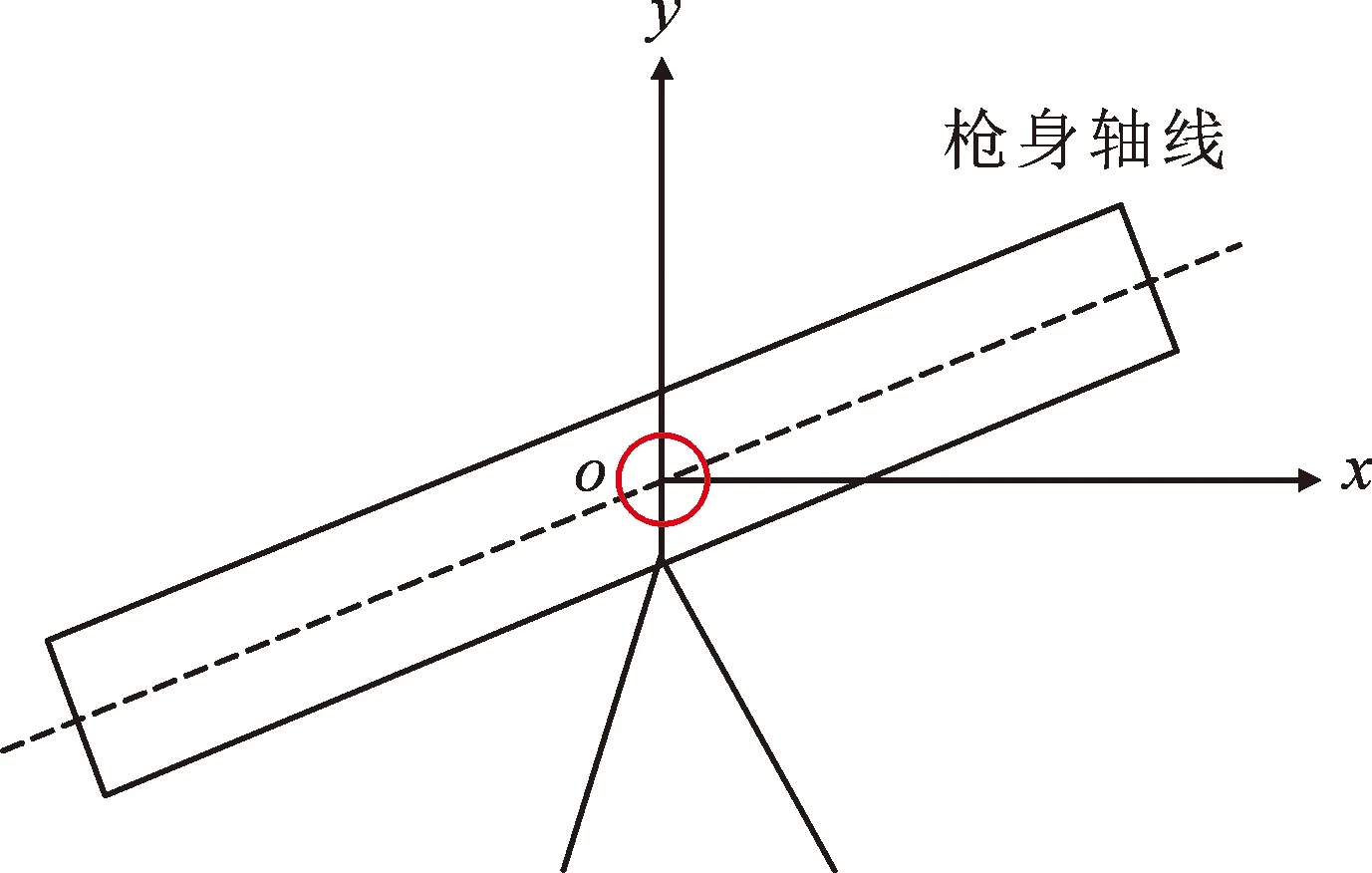
图1 狙击步枪枪身直角坐标系Fig.1 Rectangular coordinate system of the sniper rifle body
1.2 阻力系数等相关参数确定
1) 弹道系数c参数确定
弹道系数是用来衡量弹头克服空气阻力、维持飞行速度的能力的数学模型,主要由截面密度和弹头形状来决定。狙击步枪在发射之子弹的过程中,其弹丸本身所具有的形状,大小和重量对运动过程中系数产生一定的影响,一般截面密度越高,弹头形状越趋于尖形,弹道系数越高,由子弹本身的重量和子弹的直径所决定。
2) 空气密度Hτ(y)参数确定
空气密度函数表达式为Hτ(y),空气密度指在特定的温度和压力下,每单位的体积空气中所具有的质量简称为空气密度。在标准条件下(0 ℃,1个标准大气压(1 atm)),空气密度约为1.29 kg·m-1,空气密度Hτ(y)的表达式[10-11]为
(1)
式中:p为实际压力;p0为标准物理大气压;T为实际绝对温度。
3) 阻力函数G(vτ)参数确定
狙击手在纵向倾斜状态下发射子弹的过程中,子弹的飞行状态分为过渡段和稳定段两个阶段,过渡阶段为子弹在枪口飞出的一刻,受到多种气流的影响,气态特性异常复杂,多种阻力相继产生,飞行状态极其不稳定,在逐渐飞行的过程中子弹飞行稳定且以一定的速度降落称之为飞行稳定阶段,其飞行过程中受到的阻力函数为函数G(vτ)[12-13]。
(2)
式中:ρ为空气密度;vτ为气流相对流速;S为参考面积;Cx0为阻力系数。
1.3 弹道轨迹数学模型
1.3.1 纵向斜倾角度变换下的射击状态
假设士兵在实地射击时的射击角度,理想化设定射击角度为α0,考虑射击时的后坐力会使狙击枪枪口产生向上的倾斜角度(设倾角为θ),从而影响射击的精度。经查阅相关资料得知,狙击枪在射击时横向倾斜造成的偏差可以通过狙击枪下搭配的支架来消除,可忽略不计,而纵向偏差则不能通过此方法消除,因此本文着重分析狙击枪的纵向偏差来提高狙击枪的精准度。设枪口的位置为P点,在坐标轴中的坐标为(x,y)设枪管的长度为L,射击时改变倾斜的角度后枪口的位置为Ρ0点,其位置坐标为(x0,y0)狙击步枪射击状态与纵向倾斜状态原理图如图2所示。
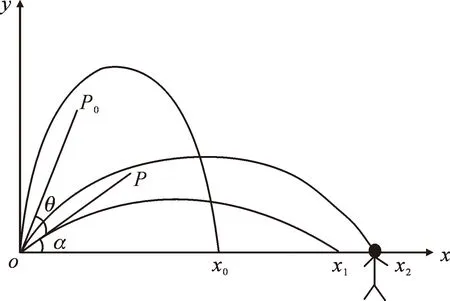
图2 狙击步枪射击状态与纵向倾斜状态原理图Fig.2 Schematic diagram of shooting state and longitudinal tilting state of the sniper rifle
图2中枪身o-P纵向倾斜角度为α,理想状态下(不考虑风力,阻力等外界因素下)射中目标时,子弹运动轨迹为o-x2;而在考虑外界因素以及子弹本身阻力的情况下则为o-x1,变换纵向倾斜角度θ,o-P0射击方向,当考虑阻力以及外界因素的情况下子弹运动轨迹为o-x0,分析可得:子弹发射过程中阻力作用会使子弹速度衰减,造成一定的纵向偏差,因此必须进一步修正才可击中目标。
1.3.2 模型的建立
根据狙击步枪纵向倾斜状态下射击状态的原理建立弹道轨迹如图3所示,在建立的直角坐标系下,以狙击枪枪口为坐标原点o,以水平位置建立o-x轴,以垂直方向建立o-y轴。纵向倾斜角度产取固定值,在子弹飞行的过程中找出子弹质心位置,并根据平面直角坐标系进行投影。
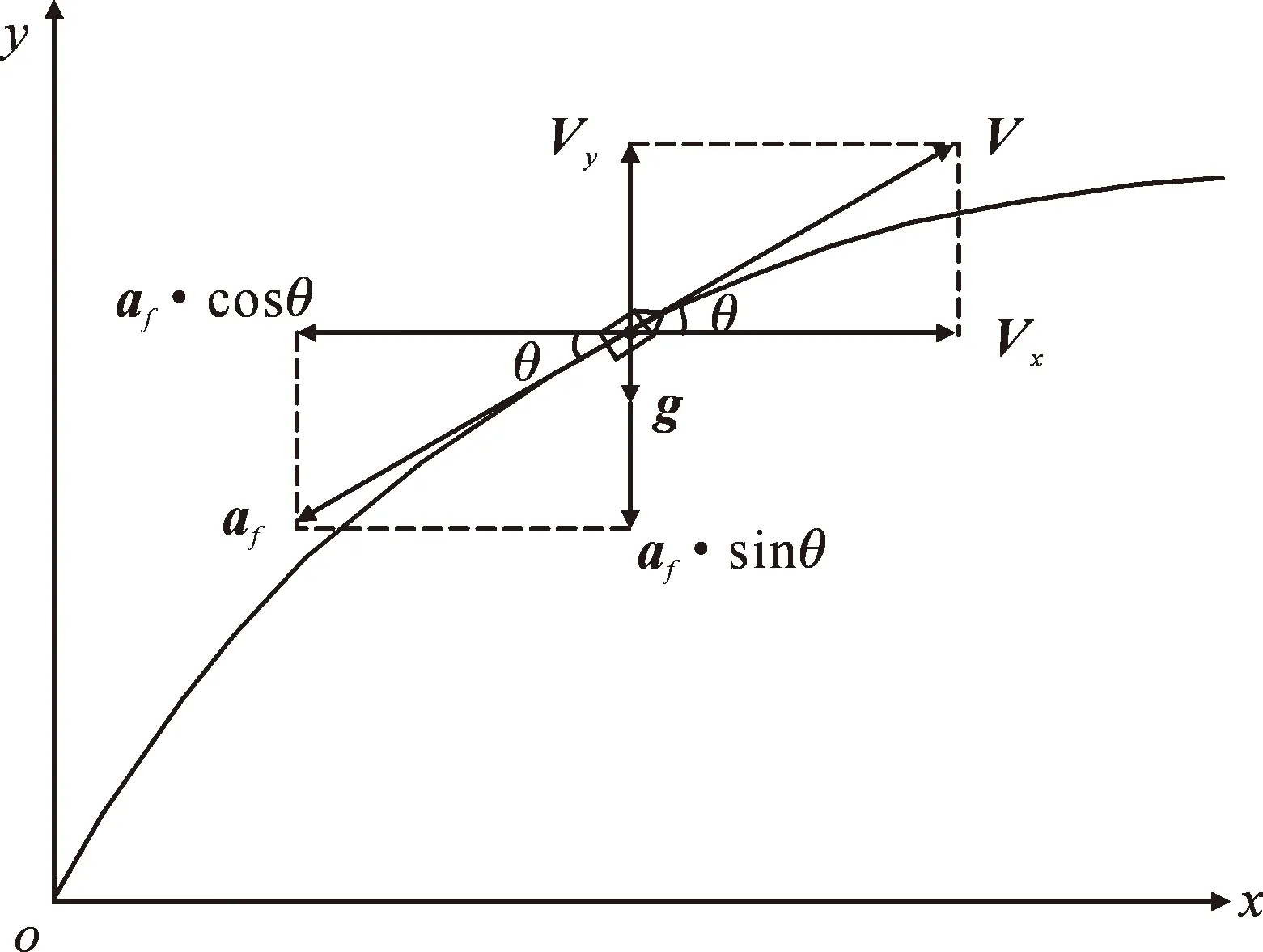
图3 直角坐标系中的子弹Fig.3 Bulletsin the rectangular coordinate system
假设枪身在纵向倾斜状态下子弹在运动中在直角坐标系中的位置为(x,y),与水平位置的夹角为θ,则vx和vy的表达式分别为
vx=dx/dt。
(3)
vy=dy/dt。
(4)
由子弹速度沿x和y轴投影可得水平速度和垂直速度分别为
vx=v·cosθ。
(5)
vy=v·sinθ。
(6)
式(5)和式(6)中vx和vy对t作微分并结合外弹道子弹运动理论可得
(7)
(8)
式中:g为重力加速度;af为阻力加速度;c为弹道系数;Hτ(y)为空气密度函数;G(vτ)为阻力函数。
1.3.3 子弹轨迹仿真
本文利用Matlab进行子弹弹道仿真,求解弹道算法为目前使用较多的四阶龙格-库塔法[14-16]。由于狙击枪射击需要的条件比较苛刻,因此通过Matlab软件来模拟狙击枪在纵向倾斜状态下射击的全过程,考虑到弹道系数、空气密度和阻力函数等条件,模拟出子弹运行轨迹和理想情况下进行比较。
利用Matlab语言关于弹道微分方程有阻力和无阻力的程序,设定狙击枪击发的具体参数为:重力加速度g=9.81 m·s-2,子弹初速度为800 m·s-1,射击角度为45°。
图4~图9分别为在一定的水平方向上弹道高度、子弹飞行距离、子弹垂直方向速度、水平方向速度、弹道曲线以及子弹运动过程中角度的变化曲线图。
图4 弹道高度的变化曲线Fig.4 Trajectory altitude curves
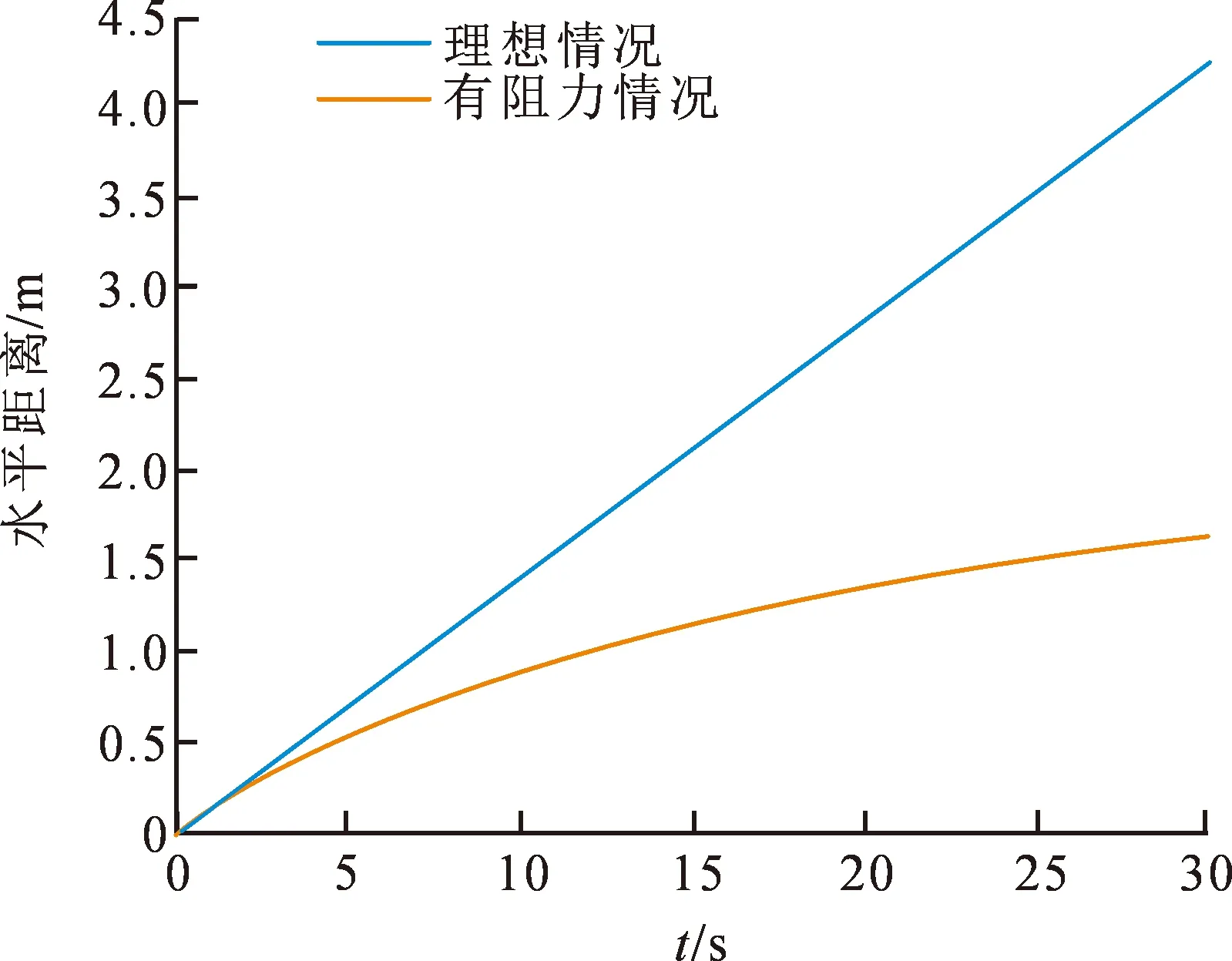
图5 子弹飞行距离变化曲线Fig.5 Curves of the bullet’s flight distance
从图4~9可看出,子弹在飞行过程中阻力函数和空气密度的影响不可避免,由于受到阻力等其他因素的影响,子弹在飞行过程中速度会一直减小,达到最高点速度垂直速度为0;理想情况下,子弹的运动轨迹遵循牛顿运动定律,有阻力的情况下,子弹弹道最高为1 018.9 m,速度为59.8 m·s-1,飞行距离为1 657 m,飞行时间为22.0 s;垂直方向速度减缓,速率由大变小,这与子弹运动的速度有关系;子弹与水平位置的夹角先减小后增大,到达目标时与水平方向的夹角为68.1°。纵向倾斜造成的方向偏差量会随着射击距离及纵倾角度的增大而增大,因此需对射击的偏差量进行分析且对风偏系数以及气压进行修正,以更好地提高狙击步枪的射击精度。
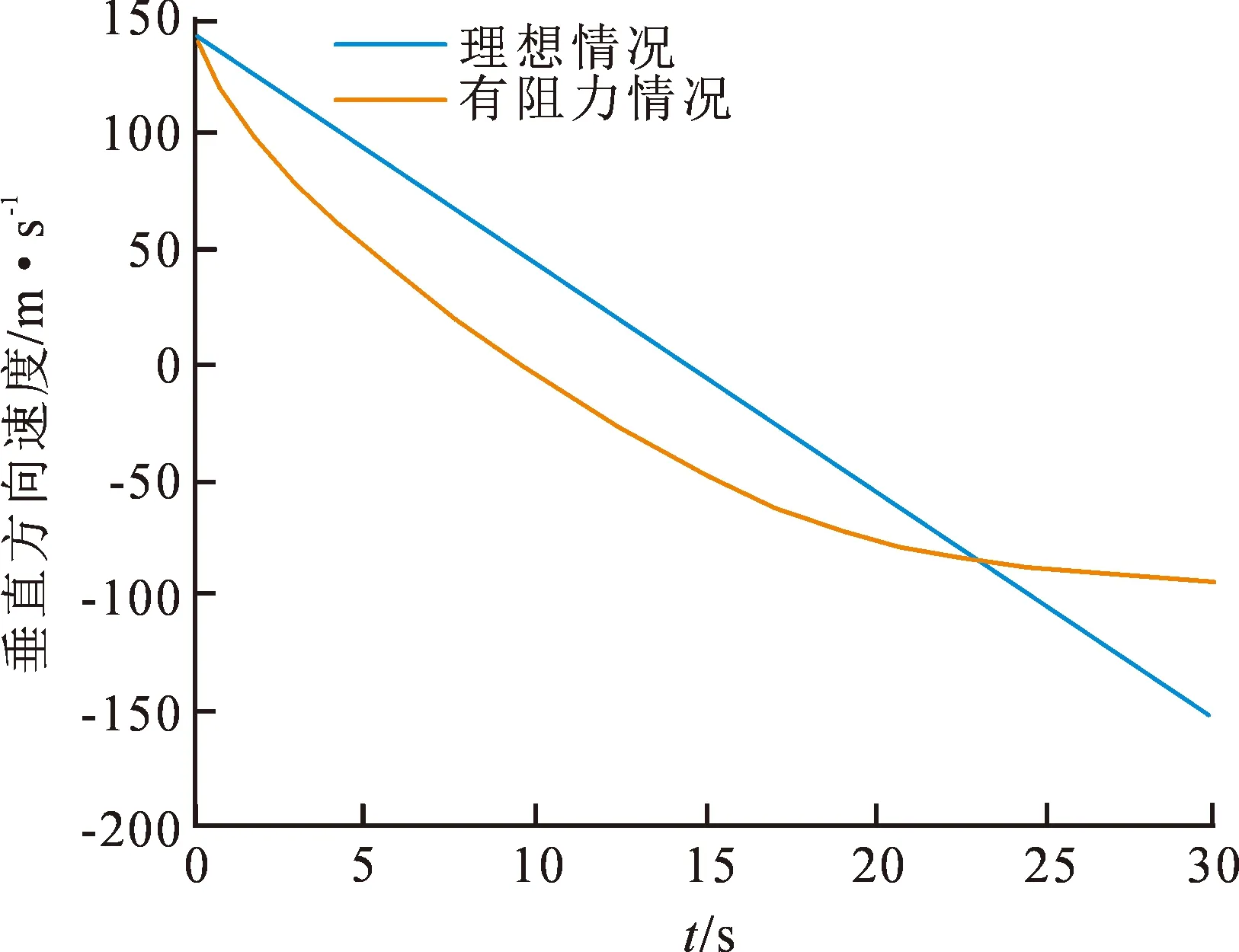
图6 子弹垂直方向速度变化曲线Fig.6 Curves of the bullet’s velocity in vertical direction
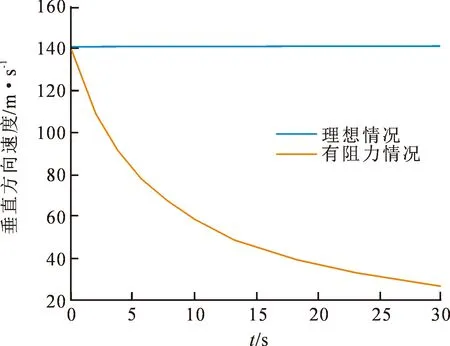
图7 水平方向速度变化曲线Fig.7 Curve of the bullet’s velocity in horizontal direction
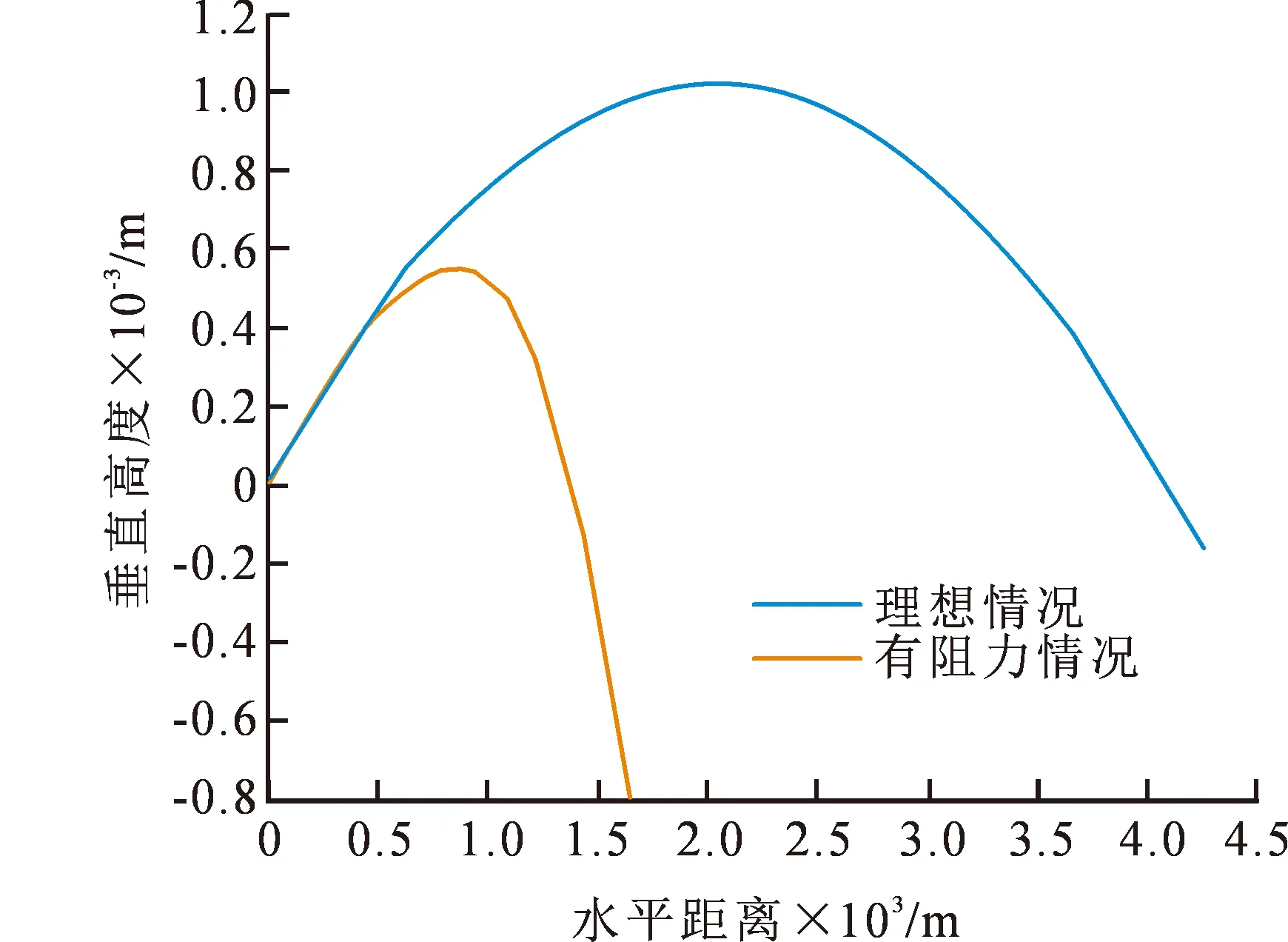
图8 弹道曲线Fig.8 Curves of ballistic trajectory
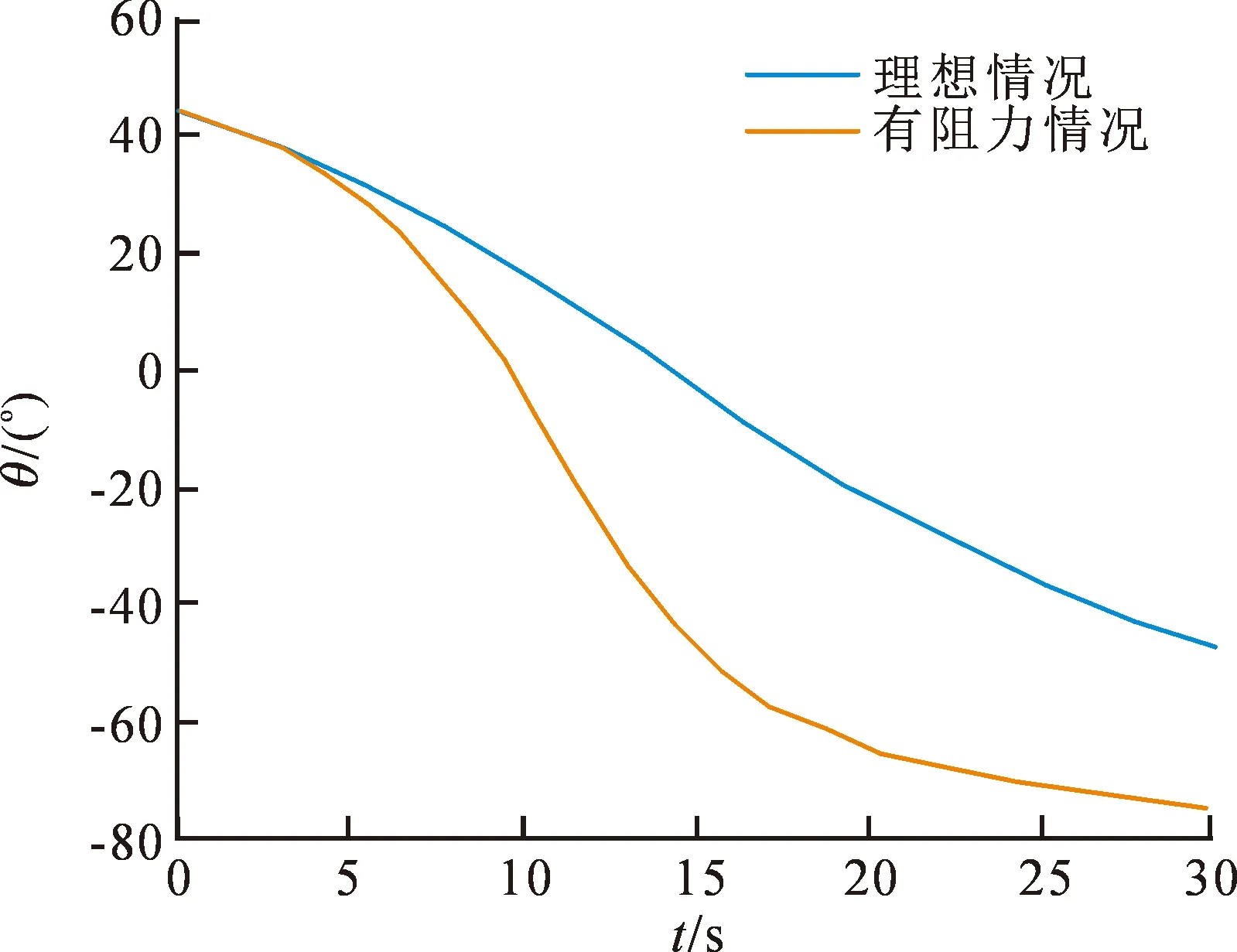
图9 子弹运动过程中角度的变化Fig.9 Change in Angle during Bullet Movement
2 射击偏差分析及误差修正
影响射击精度的主要因素为空气密度和阻力因素,在理想情况下可通过数学物理方程来解决问题,依据图2 (不考虑阻力和空气密度)可以得出真空弹道数学模型关系式为
S=2t·v0·cosθ。
(9)
v0·sinθ=g·t。
(10)
式中:θ为狙击枪枪管与水平方向夹角;S为其水平方向的运动距离;v0为飞行速度。
在理想状况下,假设狙击枪子弹出膛速度为800 m·s-1,狙击枪枪管架起的角度为45°,带入式(10)中可得其射击最远距离为2 039 m。
通过Matlab软件模拟狙击枪子弹击发后的运动过程(考虑空气密度等影响因素)算法中狙击枪的子弹出膛速度同样为800 m·s-1,射击角度为45°,模拟结果显示其实际射击距离为1 374 m,两种状况误差达32.6%,射击距离已达到不可忽略的地步,因此本文分别模拟了距离目标1 200 m,1 500 m,2 000 m及射击角度的改变,分析狙击枪射击的精确度,表1为不同纵倾角对不同目标的偏差量。
由表1可得,当射击角度为0时,由于子弹受到重力作用做平抛运动,此时子弹不可能击中目标。由表1分析可得,同一射击角度随着目标距离越近,射击的偏差越小,1 500 m的目标的偏差量比1 200 m的目标高一倍多,而2 000 m比1 500 m的目标高接近3倍,因此可以设定射击距离为1 200 m以内则可确保射击的精确度,大于1 200 m的目标要进行相应的偏差校准来保证射击的精确;对于同一距离目标,不同角度对于射击偏差相差不大。当目标在一定小的范围内,狙击手可自身判断射程距离,适当的抬高或者降低射击角度提高射击精确度,需具有长期射击经验的狙击手方能完成的事,因此需要用实验数据去设计相应的校准方法来保证任何狙击手均能用次套校准方法来提高射击精度。
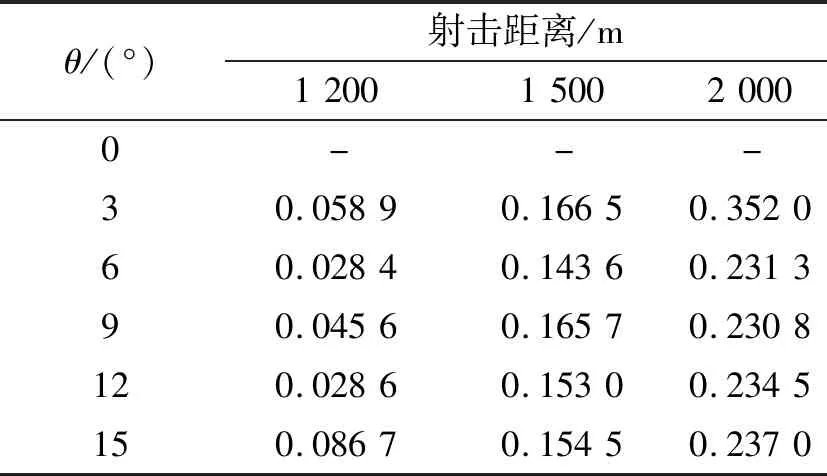
表1 不同纵倾角对不同目标的偏差量Tab.1 Deviation of different longitudinal angles to different targets
3 误差修正
在纵向倾斜状态下,为提升狙击枪的命中率,需要对子弹的弹道误差进行估算并进行有效地校准。从文献[17-19]可知,影响狙击枪命中率因素只包含弹道系数、空气密度和湿度。实际中空气密度不稳定且较难测出具体值,因此改为测定空气温度和压强,而以往的分析测试空气湿度对短距离狙击枪弹道的影响几乎可以忽略,所以本文不考虑由于空气湿度带来的弹道修正。
湿度和温度都会使得子弹弹道产生一定的偏移。由于空气中的H2O相对分子质量为18,而空气的平均相对分子质量为29,随着空气湿度的增加会使得空气平均密度降低,从而会使空气对子弹的阻力降低,同时也减缓了子弹速度的衰减,造成子弹的弹道轨迹到达目标点偏上移,温度修正系数(Tc)为
(11)
式中:T为射击环境的实际温度;T0为标准室温。
温度升高后水蒸气蒸发上升导致空气密度下降,进而导致子弹轨迹上移,一般温度差为10 ℃时,就会使得弹道纵向偏差修正量达到1 MOA;气压修正(Pc)也是弹道修正的一个关键因素,气压修正系数=标准气压/射击环境气压。标准气压为标准压强为1.0×105Pa时所对应的750 mm汞柱高度。
因此,设定射击环境温度为10 ℃,气压为650 mm汞柱,则其温度修正系数和气压修正系数分别为Tc=0.982 6,Pc=1.153 8。
则其弹道系数c为
c=C0×Tc×Pc。
(12)
其中C0为初始弹道系数,本文弹道系数选取目前常用的G1模式选择弹道系数C0=0.657 6,计算得到弹道修正系数c=0.745 5。
风偏(Wi)表达式[10,16]为
F0=166×c×SQRT(MV),
(13)
式中:R为距离;Vw为横风速度;Vm为子弹初速度;SQRT为Square Root平方根;Ew为风偏矫正。
设定射击环境风速为5 m·s-1,子弹初速为800 m·s-1,子弹弹道修正系数为0.507 2。将数据带入式(13)中可得F0=2 899.3,Ew=3.5 mil,当射击距离为1 500 m时,狙击枪专用的射击SVD瞄准镜修正圈每格为0.5 mil,则需要修正8~9格单位,具体修正见表2。
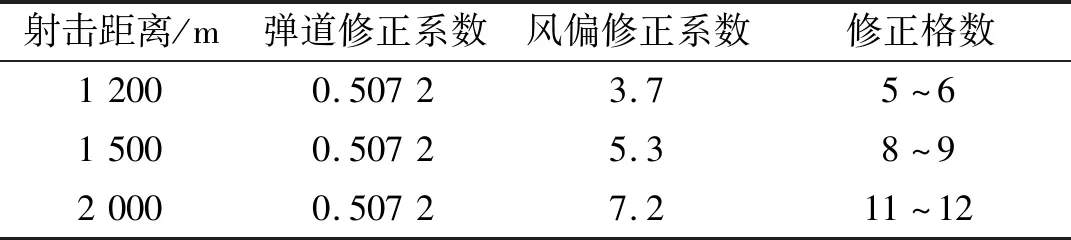
表2 瞄准镜修正格数随射击距离的变化Tab.2 The change of sight correction lattice number with firing distance
当射击环境温度湿度等条件不变时,弹道系数是一定的,由表2可得,随着射击距离的增加风偏系数也在增加,若无适当的校准,射击的偏差则会越大,当射击目标达到2 000 m时,纵向偏差由表1可知已经达到0.352 0,命中率较低,因此瞄准镜需要修正11~12格,已经达到普通SVD瞄准镜的极限,因此想要提高射击的命中率,减小纵向偏差,既要适当增加狙击枪的射速,又要减小空气阻力的影响。
狙击步枪在纵向倾斜状态射击时,因纵向角度倾斜导致子弹射击偏移,根据误差修正结果,狙击手可操控枪身的纵向角度来完成对目标的射击,射击精准度会随着枪身纵向上下倾斜的角度而改变,随着上下移动,角度逐渐增大,将其控制在一定值内,纵向方向误差较小,而随着射击距离的增大,造成的射击偏差也会越来越大。
4 结 论
1) 在考虑风速气流阻力以及外界因素对子弹速度的阻力的情况下,狙击步枪在纵向倾斜状态下射击过程中,射击精准度会随着枪身纵向倾斜角度的变化以及目标的距离变化而发生偏差,且射击的偏差量会随着射击距离的增大以及方向的偏移的增大而增大,这将对狙击手命中敌人的比例造成一定程度的影响。
2) 考虑空气密度和空气湿度的情况下,射击目标距离为1 200 m时,射击纵向偏差很小,最小达到0.058 9,命中率最高;当射击目标距离大于1 500 m时,纵向偏差量上升较快,因此必须利用瞄准镜进行一定的偏差修正来确保命中目标。
3) 在进行纵向方向偏差校准时,对风偏系数进行修正,得出修正后的弹道系数,通过瞄准镜进行偏移校准,针对不同的射击目标距离需要通过瞄准镜进行格数的校准。
