染缸排产建模及滑动时间窗启发式调度算法

隗千千，董兴业，王焕政

(北京交通大学 计算机与信息技术学院，北京100044)

0 引言

染缸排产是为多染缸、多订单、分批次的染色任务制定生产计划的问题，需要考虑生产订单分配、工艺约束、订单要求和客户要求等限制因素，是一个组合优化问题。由于缺乏可用的软件工具，我国的印染车间制定染缸排产计划时很大程度上还依赖于计划人员的经验。其染色工艺约束复杂，生产任务规模大，给计划人员带来了巨大的压力，排产方案的质量也难以保证。

近年来，许多学者在染缸排产模型及调度算法方面作了许多研究。通常，染缸排产模型主要考虑完成时间、洗缸成本、染缸切换成本等。文献[1]以最小化染色成本、洗缸成本、库存成本、延误代价为优化目标，提出了一种基于启发式规则的改进极值优化算法用于求解小规模问题；文献[2]考虑了产品拆分分批，最小化产品延误代价和切换成本，使用遗传算法求解；文献[3]考虑了订单的拆分和合并分批，以最小化延误时间和最大化染缸利用率为目标，设计了构造型启发式方法；文献[4]以延误代价和染缸利用率为目标，考虑相容作业组的拼缸、与作业顺序相关的设置时间，构建了问题模型并提出了一种多目标人工蜂群算法；文献[5]针对机器相同的排产调度问题，考虑产品分批、与作业顺序相关的设置时间等因素，以最小化完工时间为目标，设计了混合整数线性规划模型，将产品的调度过程分为批次构建和批次调度两个子问题，使用多种群遗传算法求解；文献[6]在染缸容量上限和下限约束、订单优先级约束、洗缸约束等约束条件下，使用量子遗传算法，对订单进行拆分与合并分批，可完成小规模问题的染缸排产调度。除了针对印染问题的研究，与之最相似的问题是批处理调度问题[7-10]。该类问题应用背景广泛，包括半导体生产[11]、钢铁制造[12]、轮胎制造[13]、印刷线路板生产[14]等。若简化约束条件，染缸排产调度问题属于异构并行机、作业大小不同、作业组不相容、设置时间与作业顺序相关的批处理调度问题，是NP-难问题。

实际生产中问题的规模往往很大，约束条件和生产限制因素更加复杂，对排产效率要求也比较高。一般情况下，一个染纱车间的月订单量至少有500个，染缸数量有几十个，排产调度时需要考虑产品的特殊工艺(如荧光产品)、头缸生产以及染缸的维护计划等约束。此外，现有生产计划对染缸排产还存在一定的限制。相比之下，上述对染缸排产问题的研究中所构建的问题模型未考虑特殊工艺、头缸生产、染缸维护计划、进出缸并发约束，也未考虑增量调度，与实际生产条件相差较大，限制了算法的适用性；另外，虽然文献中批处理调度问题的研究成果较多，但是这些算法不能用于本文所提出的问题模型。综上所述，染缸排产模型及优化算法在实用性和适用性方面亟待提高。

本文根据印染企业的生产需求，以最小化延误代价、染缸切换成本、洗缸成本为目标，在已有问题模型的基础上，考虑产品头缸、禁荧光、染缸维护、现有生产计划安排等新的生产约束，建立更符合实际生产条件的染缸排产增量调度模型，并基于启发式规则设计求解算法，提高排产效率，节约生产成本。

1 染缸排产调度问题模型

1.1 问题描述

染缸排产调度问题是通过对产品进行拆分分批或者合并分批将多个产品安排到多台染缸中排产，需解决的问题是在不改变原生产计划中产品批次划分的情况下，对新增产品进行批次划分，为各批次安排染缸，确定批次开始加工时间，在满足各种约束条件的同时使调度目标最优。

印染企业的生产订单首先由销售部门下发给计划部门，然后计划部门根据实际生产情况制定生产计划，并传达给生产车间。每个产品从进入企业资源计划系统到包装入库的处理过程可表示为如图1所示的顶点活动(Activity On Vertex，AOV)图。产品调度仅需要确定C4和C5的开始时间；由于排产过程不涉及C0和C6，因此它们可看作虚节点，时长为0天，其他节点的时长与具体产品有关；当产品没有头缸时，不需要工序C4。

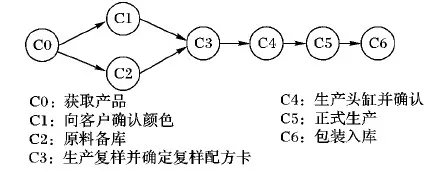
图1 生产流程AOV图Fig. 1 AOV diagram of production process

染缸排产调度问题的约束条件包括以下几个方面：

1) 染缸容量限制约束。批次加工量必须在所选染缸容量上限和下限之间，相同的容量上限为同一缸型。

2) 染缸维护时间约束。染缸有多个维护时间段，维护期间染缸不可用。

3) 加工时间约束。图1中各工序在执行前，其前序工序必须完成，否则应延迟排产，延迟时间为其前序工序的最大准备时长。

4) 禁荧光约束。染缸加工荧光产品后需连续加工一定缸数的非荧光产品之后才能加工禁荧光产品。

5) 进出缸并发约束。批次在开始加工前和加工结束后有进缸和出缸操作，同一时刻执行进缸和出缸操作的数量有一个上限，该限制和工人资源量有关。

6) 拼缸约束。几个产品合并在一个批次加工时，称为拼缸；拼缸批次的各产品必须来自同一产品组。

7) 拆缸约束。一个产品拆分成几个小的批次加工以适应染缸容量，称为拆缸。为了保证大货产品的生产质量，不同量级的产品的最小拆分阈值不同，拆分的各个批次中，最多有一个批次的生产量小于该拆分阈值，拆缸需尽可能拆分成大的批次；原生产计划中已经拆缸的批次不允许再次拼缸；头缸不允许拆缸。

8) 原生产计划中已经拆缸或者拼缸的产品，再次调度时不再进行批次划分。

本文首先对数据作了预处理：依次检查产品的各项工序，计算产品的延迟排产时间，记为产品的释放时间。例如，某产品的C1、C2、C3工序未完成，则其延迟排产天数为上述三工序的最大准备时长。由加工时间约束可知，产品的最早加工时间应不早于释放时间。

1.2 模型构建

1.2.1 符号定义

1)集合和索引。

M为染缸集合，索引m；J为产品集合，索引i、j；B为批次集合，索引b、c；Jb为批次b的产品集合，Bj为产品j的批次集合；F为产品分组集合，索引f，Jf为组f的产品集合；FL_J为荧光的产品集合，FL_B为荧光的批次集合，FL0_J为禁荧光的产品集合，FL0_B为禁荧光的批次集合；SP为并发时间段集合，SMm为染缸m的维护时间集合，索引sp。

2)变量。

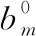
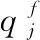
mb表示批次b使用的染缸，sb为批次b的开始加工时间，eb为批次b的结束加工时间，tb为批次b的染色类型；qjb表示产品j在批次b中的加工数量，hjb表示产品在批次中的生产状态(若产品j在批次b中为头缸，则值为1，否则为0)。

Stt′为从染色类型为t到染色类型为t′的洗缸时间；Pju为产品j在缸型为u的染缸的加工时长；ssp为时间段sp的开始时间，esp为时间段sp的结束时间，nsp为时间段sp的进出缸并发数量。

3)参数。

Z表示头缸未确认时延迟排产时长，U表示批次任务的出缸时长，L表示批次任务的进缸时长，V表示荧光批次和禁荧光批次间隔序列长度，P表示进出缸最大并发数目。

1.2.2 模型表示

在染缸排产建模时，目标函数中主要考虑排产延误、洗缸成本、染缸切换，而模型实用性主要体现在约束条件中。

用S表示一个可行解，则每个染缸的执行序列为一个部分解，染缸m部分序列可表示为Sm=(b1,b2,…,bk)。同一产品的不同批次之间更换染缸会造成批次的质量差异，产生染缸切换成本，染缸m上的批次序列的染缸切换成本为：

(1)

其中：

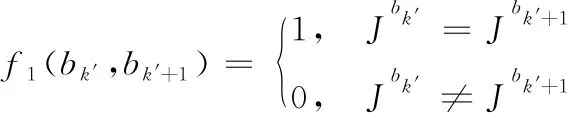
(2)

同一染缸的相邻批次之间需要洗缸，洗缸时间与相邻批次的染色类型有关，染色类型有白、浅、中、深四种，一般来说，浅色批次到深色批次的洗缸时间小于深色到浅色批次的洗缸时间。Stt′表示加工完染色类型为t的批次后，在加工染色类型为t′的批次之前的洗缸时间。染缸m上的批次序列的洗缸成本为：

(3)

每个产品都有交货日期，延期交货会有一定的惩罚，惩罚大小取决于产品的优先级权重和延误时长，产品j的延误代价可表示如下：

(4)

其中：

cj=max{eb|b∈Bj}

(5)

目标函数及约束条件如下：

(6)

s.t.

(7)

lap(sp,b)=0； ∀m∈M,sp∈SMm,b∈Sm

(8)

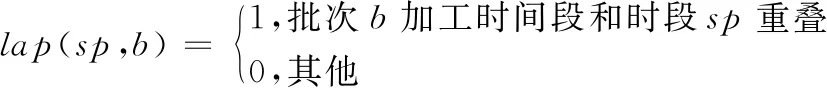
(9)

min {sb}≥rj;∀j∈J，b∈Bj

(10)

In(f0(b,Sm),Sm)-In(b,Sm)≥V;

∀m∈M,b,b0∈Sm,b∈FL_B

(11)

nsp≤P;∀sp∈SP

(12)

fj1=fj2;∀b∈B,j1,j2∈Jb

(13)

|MBj|≤1;∀j∈J,b∈Bj,MBj={b|qjb≤thj}

(14)

(15)

(16)

qjb,sb,eb∈N

(17)

式(6)定义了调度目标，是染缸切换成本、洗缸成本和延误代价三项成本的线性和。

式(7)表示染缸容量约束，批次加工量(各产品在该批次中加工量之和)应在染缸容量上限和下限之间；式(8)和式(9)表示染缸维护时间约束，任意批次的加工时间都不与染缸维护时间重叠；式(10)表示加工时间约束，产品的任意批次开始加工时间都晚于释放时间；式(11)表示禁荧光约束，荧光批次b与其之后的第一个禁荧光批次之间至少间隔V个批次；式(12)表示进出缸并发约束，任意时间段sp执行进出缸操作的数量少于P；式(13)为产品的拼缸约束，批次中加工的产品都属于同一产品组；式(14)为产品的拆缸约束，产品最多有一个批次加工数量小于拆缸阈值；式(15)为头缸拆缸约束，若在批次中加工头缸，则加工量为全部头缸数量，即头缸不允许拆分；式(16)为产品加工数量约束，产品总量等于已完成数量与各个批次加工数量之和；式(17)为变量的整数约束，即时间变量、批次数量均为整数。

问题模型中已知染缸数据、产品数据、现有生产计划、排产参数等数据，求解产品的分批方案和新的排产计划，其基本问题是并行批处理调度问题，已被证明是一个NP-难问题[15]，因此其衍生问题也是一个NP-难问题，采用传统的数学规划方法无法有效求解。染缸排产调度问题约束条件复杂，批次划分和调度时间都是离散的，时间跨度较长，染缸和产品的数据规模较大，因此依据问题特点和模型约束，设计构造型启发式方法快速求解是实际生产的迫切要求。

2 染缸排产调度优化算法

为简化问题，作出如下假设：图1中工序C1(向客户确认颜色)、C2(原料备库)、C3(生产复样并确定复样配方卡)的状态随调度日期更新，产品的释放时间也随之更新；批次一旦开始加工，就不能被中断；当一个批次加工完成后，就从产品的原计划生产列表中删除，不再对下次调度产生影响；由于产品的头缸不能拆缸，因此假设所有头缸均存在单独加工的缸型；缸型相同的染缸，其容量下限也相同；批次加工时间精确到分钟，释放日期、交货日期精确到天。

图2中所述产品调度算法是根据染缸的可用状态和当前进出缸并发状态，计算产品j最佳的分批方案和批次加工时间，基本步骤如下：

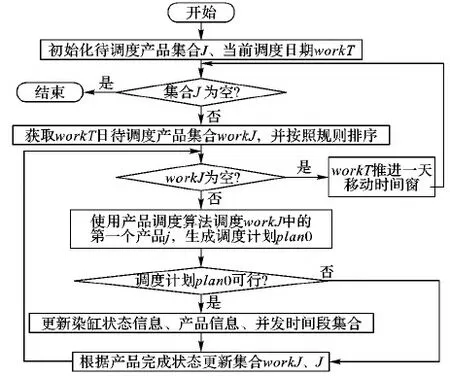
图2 STWS算法流程Fig. 2 Flowchart of STWS algorithm

步骤1 若产品j的原计划批次集合Bj不为空，则转至步骤6；否则生成拼缸调度计划PlanCj(动态拼缸算法)，即拼缸批次bj。

步骤2 若PlanCj不存在，则转至步骤5；否则若PlanCj加工开始时间在workT内，Planj←PlanCj，算法结束。

步骤3 若|Jbj|>1，则生成|Jbj|≤1的计划PlanC0j(动态拼缸算法)；否则转至步骤5。

步骤4 若PlanC0j存在且不会发生延误，则Planj←PlanCj，算法结束；否则若产品当前加工部分不可拆缸，则算法结束。

步骤5 生成拆缸计划PlanSj(拆缸算法)，令Planj←PlanSj。

步骤6 调整PlanSj批次，选择合适的染缸和加工时间(批次最佳排序算法)，优化延误代价、换缸成本、洗缸成本，算法结束。

在使用动态拼缸算法和基于回溯搜索的拆缸算法对产品进行调度时，需要确定产品的待调度数量和产品的最晚加工完成日期。不同状态下的产品调度数量不同，主要和头缸有关，根据约束条件(15)和(16)，可得产品j的待调度数量qj′的计算方法为：

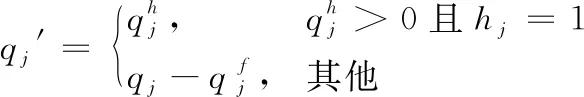
(18)

为降低延误代价，产品发生延误时，应该保证延误最短，因此，在产品调度过程中，初次调度最晚加工完成日期(截止日期)均为交货期，在不能成功调度时，最晚加工完成日期每次延后一天，进行迭代调度。

2.1 动态拼缸算法

动态拼缸(Dynamic Combination Batch，DCB)算法首先根据当前调度时间workT选择满足并发约束(12)的染缸集合。然后在同一最晚加工时间之前，对于集合中的每个染缸上，计算拼缸方案，将该组合问题转化为一维背包问题，使用动态规划算法计算产品j的最佳拼缸产品集合，并确定拼缸批次的加工时间，选择第一个可行的拼缸批次返回。若所有拼缸批次都晚于最晚加工时间，则推迟该时间点，重新查找拼缸方案。最后是优化阶段，在可用染缸集合中查找拼缸批次评价指标最小的染缸，确定批次所用染缸及开始加工时间。以下是DCB算法伪代码描述。

算法1 动态拼缸算法。

输入：待调度产品j；

输出：拼缸批次b。

计算产品j的可拼缸产品集合combJ：

combJ={j′|j′∈J,j′∈Jfj,rj′≤workT}

计算产品j和combJ中产品的待调度数量

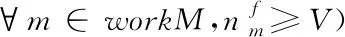
IF(workM为空) RETURN NULL

初始化最晚加工完成日期combD←dj，拼缸标记combF← false，染缸访问序号i← 0

WHILE (true)

WHILE (i<|workM|)

计算满足容量约束(7)的拼缸产品组合combJmi

IF (combJmi为空)i←i+1

ELSE

计算b在mi的加工时间，令combF← true

IF (eb≤combD) BREAK

ELSEi←i+1

END WHILE

IF(combF==false) RETURN NULL

ELSE

IF (eb≤combD) BREAK

ELSE 更新combD←combD+1，i← 0

END WHILE

workM′为workM中满足批次b容量约束的染缸，计算b在workM′中各个染缸mi的加工时间，得到新的批次bi，则可行批次集合comB={bi|ebi≤combD}

计算bi∈comB所用利用率prbi和洗缸代价csbi，选择拼缸批次评价指标Cbi最小的批次b；RETURNb

上述染缸利用率和缸批次评价指标的计算方式为：

(19)

Cbi=umi(1-prbi)+csbi

(20)

2.2 拆缸算法

2.2.1 基于回溯搜索的拆缸算法

由于产品拆缸有最小阈值限制，并且产品拆分时尽可能拆分为大的批次，若使用简单贪心算法直接选择最大容量的染缸进行拆分，会产生很多拆缸方案不可行的情况，因此本文提出基于回溯搜索的拆缸算法(Batch split Algorithm based on Backtracking Search， BABS)。

BABS是一种隐枚举算法，计算满足约束条件最佳拆缸方案，由大到小选择染缸，在每个染缸上尽可能地续缸生产，直至拆缸不可行，此时删除当前方案中已安排的最小染缸，回溯查找可用染缸，然后继续分批，其伪代码描述如下。

算法2 基于回溯搜索的拆缸算法。

输入：待调度产品j；

输出：拆缸方案PlanSj。

计算产品j的待调度数量qj′

获得可用染缸workM，按缸型降序、可用时间升序排序

初始化最晚加工完成日期splitD←dj

初始化基本变量：可延误拆缸标记splitF← false，拆分批次集合PlanSj← NULL，所用染缸的可加工最大量uC← 0、最小量lC← 0，染缸访问序号i← 0

WHILE (true)

从i开始顺次查找第一个满足式(21)或(22)的染缸mi

IF (mi不存在)

WHILE (PlanSj!=NULL)

回溯查找新的可用染缸mi；BREAK

END WHILE

IF (mi不存在)

IF (splitF==true)

//可延期拆缸

splitD←splitD+1，重新初始化基本变量

CONTINUE

ELSE 产品拆缸失败，算法异常结束

WHILE (true)

IF (mi满足式(21)或(22))

在染缸mi上生成新的批次b

ELSE BREAK

IF (eb>splitD)

//可通过延期拆缸

更新splitF← true，i←i+1；BREAK

ELSE

lC←lmi+lC，uC←umi+uC

PlanSj←PlanSj∪b

END WHILE

IF (lC≤qj′≤umi) BREAK

END WHILE

调整PlanSj批次的加工数量，使相同缸型的批次加工数量尽可能均匀；RETURNPlanSj

回溯查找染缸的方法：首先删除PlanSj最后加入的批次newb，然后令i← 0，从i开始顺次查找第一个比newb所用缸型小且满足式(21)或式(22)的染缸mi。

染缸可用条件判断式：

lmi+lC≤qj′≤umi+uC

(21)

lmi≥thj并且lmi+lC≤qj′

(22)

2.2.2 拆缸优化算法

上述基于回溯搜索的拆缸算法中的基本准则是优先选择大缸，查找满足染缸容量约束和产品拆缸约束的拆缸组合方案，这种方式得到的拆缸方案大多使用染缸的缸型种类比较多，一个产品需要在多个染缸上生产，染缸切换成本比较高，产品质量稳定性也变差，因此最佳的拆缸方案是在较大的缸中续缸(而不是选择最大的染缸和较小的染缸拆缸)。

拆缸优化(Batch Split Optimization，BSO)算法是在基本拆缸方案的基础上，保证最晚加工完成时间相同、使用拆缸批次数量相同和优先选用大缸的准则，优化洗缸成本和染缸切换成本。每一轮优化都是在同一个最晚加工完成时间前，将生产量均分到较小的染缸中，如果不可行，则保留最大的一个批次，均分剩余加工部分，直到所有批次都被保留或者得到可行方案。以下是算法的伪代码描述。

算法3 拆缸优化算法。

输入：基础拆缸方案PlanSj；

输出：优化拆缸方案OPlanSj。

根据计算产品j的待调度数量qj′

获得可用染缸workM，可用缸型typeM，按缸型降序、可用时间升序排序

根据PlanSj计算最晚加工完成日期splitD=max {eb|∈PlanSj}

初始化待拆缸数量n← |PlanSj|，所用染缸的可加工最大量uC← 0、最小量lC← 0；将PlanSj按照缸型从大到小排序

IF (n==1) RETURNPlanSj

WHILE (|PlanSj|>1且n>1)

在typeM中查找n缸可加工qj′的染缸m：

n*lm+lC≤qj′≤n*um+uC

IF (染缸m不存在)

删除PlanSj中使用染缸缸型最大的批次bmax，

OPlanSj←OPlanSj∪bmax

ELSE

在splitD之前，在所有缸型为um的可用染缸中优先续缸加工n个批次，加入集合OPlanSj中

END WHILE

调整OPlanSj批次的加工数量，使相同缸型的批次加工数量尽可能均匀；

RETURNOPlanSj

2.3 批次最佳排序算法

使用BABS计算产品j的拆缸方案PlanSj(|PlanSj|>1)时，仅考虑交货日期之前每个染缸上的最大加工能力，优先选择了开始可用时间最早的染缸。由于染缸有维护计划，可能发生这种情况：可用时间最早的染缸，其维护时段很长且开始时间很早，进而可用时间段相对其他同缸型的染缸较短，批次选择染缸数目较多。一方面会增加洗缸成本，另一方面也会增加切换成本，导致产品质量不稳定。

在原生产计划中已经拆缸或者拼缸的产品，产品的批次划分已经确定，但是具体的染缸未确定，因此需要确定合适的染缸以及加工时间。

以上两种场景都需要进行批次调度，本文设计了批次最佳排序(Batch Optimal Sorting，BOS)算法，调整批次在各个染缸上的生产顺序，使得产品j的延误时间最短，染缸切换成本、洗缸成本最小。将产品的各个批次按照缸型分组，对使用同一种染缸缸型的批次，统一在指定缸型的染缸上调度，每一组都搜索一个最长续缸方案。以下是算法步骤描述：

步骤1 设置最佳方案最晚加工完成日期combD为max{eb|b∈PlanSj}。

步骤2 将PlanSj中的批次按照批次所使用缸型降序排序，计算PlanSj使用的所有染缸缸型集合MType，设置MType访问序号i为0，最佳调整方案为OPlanSj。

步骤3 对染缸进行筛选，获得指定缸型染缸workM。

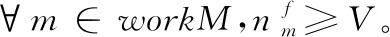
步骤4 若访问序号i≥|PlanSj|，则批次调整完成，算法结束；否则，获得PlanSj中使用染缸缸型为tyi的批次Btyi，获得workM中缸型为tyi的染缸Mtyi。

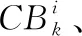
(23)

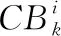
2.4 进出缸并发控制策略

由于整个调度过程是按照时间先后顺序进行的，并发时间段的占用不可逆，调度时每个批次可用时间段仅和当前并发状态和染缸状态相关。

上述DCB算法、BABS、BSO算法和BOS算法在查找批次在染缸上的可用时间段时，需要严格满足染缸的维护时间约束和并发时间段约束(进出缸时间段同时满足并发约束)；产品生成可行计划后，按照批次的时间先后顺序，依次分配到指定染缸上，每分配一个批次，都重新划分时间段，更新集合SP以及各时间段的并发数量nsp。

3 实验评测

本章首先给出了实验所用的参数和数据集，然后将STWS算法与人工排产方案进行对比，最后对算法的增量调度进行评测。

本文所使用的产品和染缸数据均从真实数据集中随机抽取，调度日期为2018年4月1日，染色类型均匀分布。

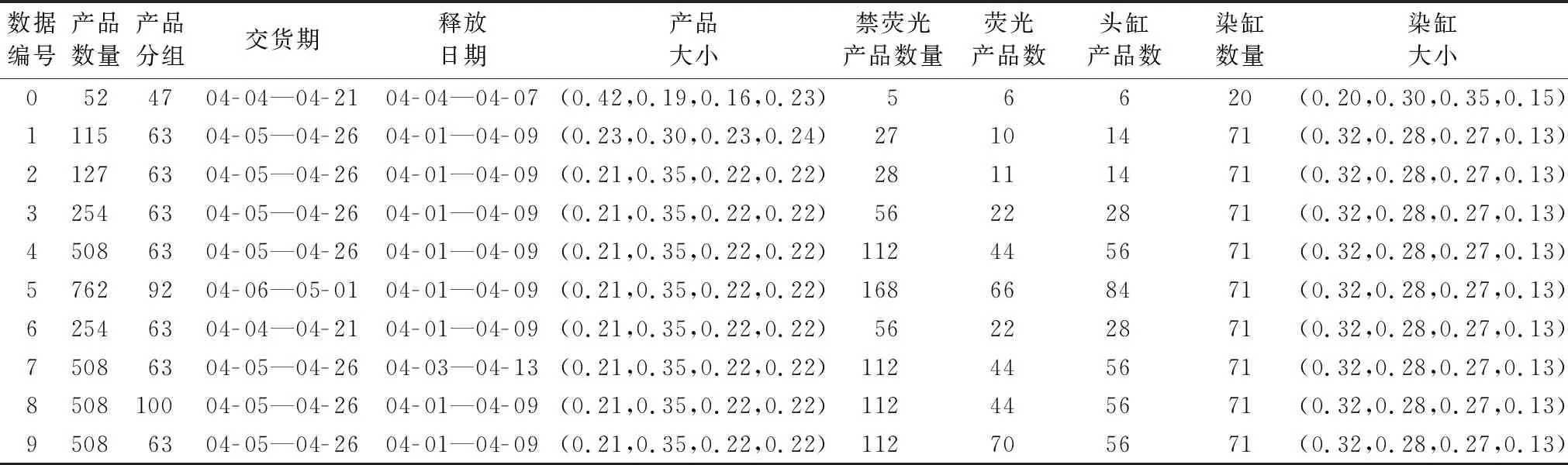
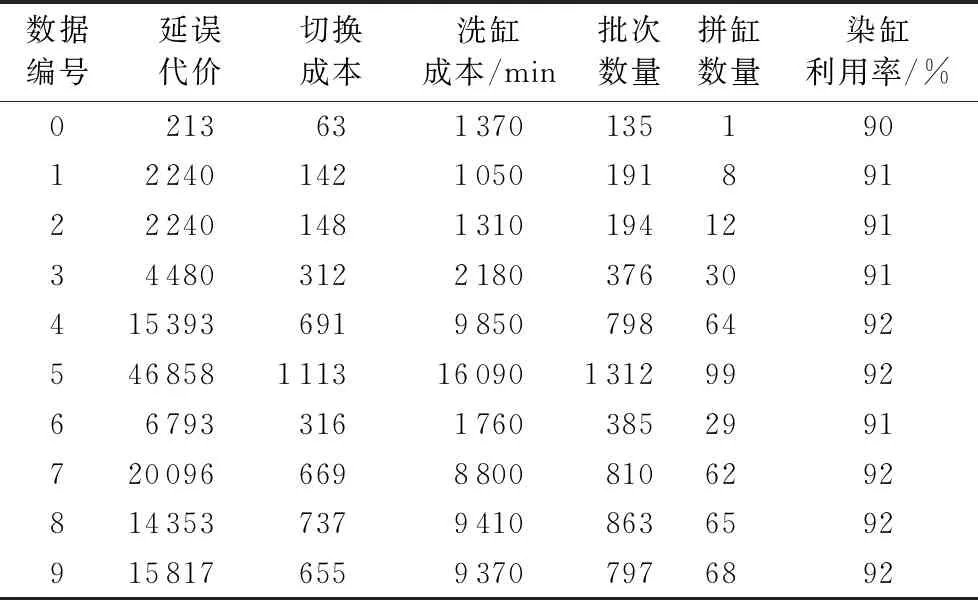
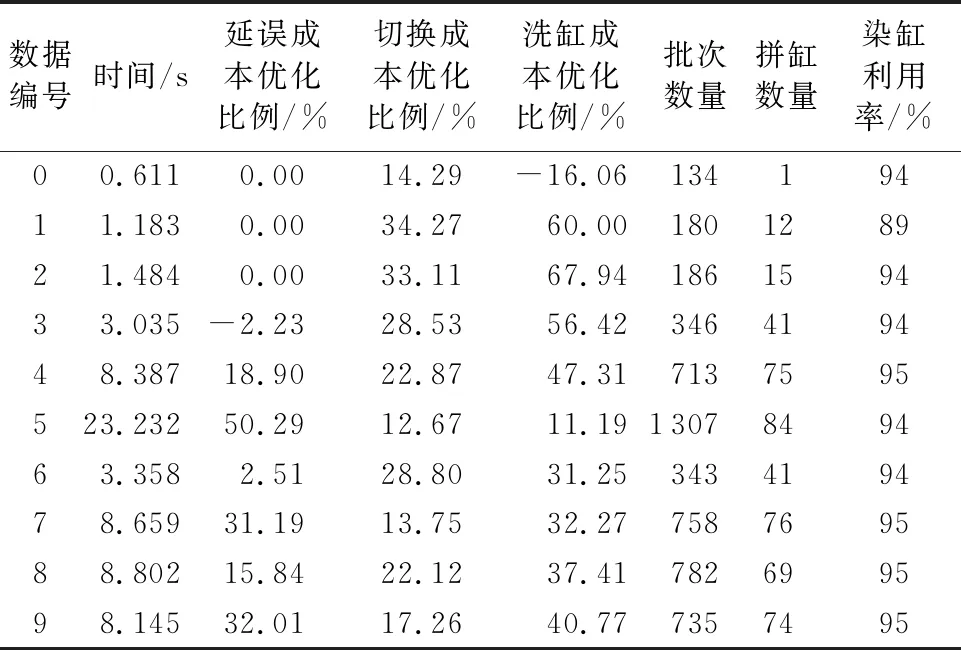
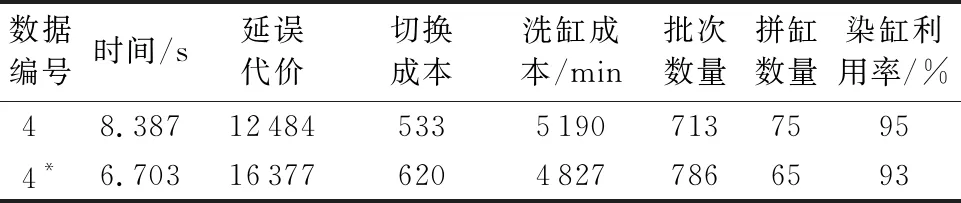
根据产品生产量将产品分为4类：小(1≤qj≤100)、中(100

表1列出了算法需要的参数取值列表。

表2列出了实验中使用的测试数据集，其初始调度计划均为空。其中第6组数据是第3组数据的各个产品的交货期整体提前1～5天所得，其他数据与3号相同，第7、8、9组数据是对第4组数据部分处理得到的：第7组数据延迟了产品的释放日期；第8组数据减小了可拼缸数目，即在产品数量相同的情况下增加了分组数目；第9组数据增加了荧光产品所占比例。

表1 参数取值列表 Tab. 1 List of parameter values

表2 实验中使用的数据集 Tab. 2 Dataset used in the experiment

人工排缸方案一般是由经验丰富的计划员完成，约束执行往往不是很严格，当实际排产发生约束冲突时，只能通过延迟染缸的后续批次或者取消某些批次来缓解，使得排产不能按照原计划实施。这里使用普通规则(General Rule，GR)算法来模拟人工排缸过程，并与STWS算法对比。与STWS类似，GR算法是按照产品的优先级顺序(交货日期升序、产品优先级权重降序、释放日期升序排序)，依次对产品进行调度；但是GR算法在产品调度时没有使用最优调度策略，而是使用贪心方法对产品进行拆缸和拼缸；批次调度时，选择洗缸时间最短的染缸依次调度，不再进行迭代优化。表3为GR算法的调度结果。

表3 GR算法调度结果 Tab. 3 Scheduling results using GR algorithm

使用STWS进行调度，可得到如表4所示的调度结果，其中，延误成本优化比例=(GR算法延误成-STWS算法延误成本)/GR算法延误成本，同理可得切换成本优化比例、洗缸成本优化比例。从调度结果可以看到，在数据规模适中(产品数量在100到500左右)的情况下，该算法可在10 s内给出可行方案。相对于GR算法，STWS算法的染缸切换成本、洗缸成本明显减小，批次数量有所减少、拼缸批次有所增加，染缸利用率明显提高，以上结果说明动态拼缸算法和拆缸算法有利于更好地利用染缸的生产能力；在延误代价方面，当数据规模较大时，STWS算法优化效果显著，最高可优化50%以上，数据规模较小时，优化不明显，这是因为产品数据较少时，可优化空间也有限；除第0组数据外，洗缸成本均有大幅度降低，说明批次最佳排序算法能有效安排同一产品的不同批次进行续缸生产，从而节约了洗缸成本；对于第0组数据，洗缸成本上升的主要原因是批次调度时为增加续缸而选择了首次洗缸成本较高的染缸。综合以上几个方面，STWS算法性能优于GR算法。

表4 STWS算法相比GR算法的优化结果 Tab. 4 Optimization results of STWS algorithm compared to GR algorithm

从表4的第4、7、8、9组数据的调度结果可以看到，在数据规模适中时，无论什么特点的数据，STWS算法性能都比较稳定，延误代价优化程度稳定在20%～30%，切换成本优化程度在10%～20%，洗缸成本优化程度在30%～50%，总体优化效果都较为明显。

第4组数据的产品数据是在第3组数据的产品数据的基础上加入了一些新的产品得到的，因此将第3组数据的调度计划作为第4组数据初始计划用于增量调度测试，表5为增量调度结果。相对于第4组数据的无初始调度计划的调度结果，增量调度的消耗时间短，这是由于增量调度时调度计划中已经分批的产品不再经过分批过程，从而节约了调度时间。不过，由于已调度过的产品的批次划分不能改变，减小了优化空间，因此各项成本值均有所增加，拼缸批次数量减少，染缸利用率有所降低。

表5 STWS算法在第4组数据上的增量调度比较 Tab. 5 Incremental scheduling of STWS algorithm on the 4th data

4 结语

根据印染车间的生产需求，考虑产品的多样化、异构并行机、批次划分约束、头缸约束、禁荧光约束、染缸维护计划等实际场景，建立了染缸排产增量调度模型。本文提出了构造型启发式算法——滑动时间窗调度(STWS)算法，按照一定的规则和逻辑对产品进行调度，最小化延误代价、洗缸成本、染缸切换成本。产品调度过程中，设计了动态拼缸(DCB)算法和拆缸算法(BABS、BSO)进行批次划分，使用批次最佳排序算法调度批次。通过实验对比，检验了STWS算法增量调度的性能，在数据规模适中时，STWS算法能够在10 s内给出可行方案，相比人工排产方案，该算法显著地降低了生产成本和延误代价，目前已在某企业的生产系统中上线运营。

由于算法大多数场景都是增量调度模式，批次划分仅限于第一次调度的产品，批次划分确定后，批次的调度是影响生产代价的重要因素，因此批次调度的全局优化是接下来的研究重点。