一种信息不完备条件下的艇员弃艇脱险决策模型研究
2020-03-05
(海军潜艇学院,山东 青岛 266071)
0 引言
从理论上说,当潜艇发生海难事故后,艇员在舱室等待援救是比较安全的方法。但是,实际情况往往是等不到外部援救抵达,舱室情况即快速恶化而不得不弃艇脱险。如果指挥员过早下达弃艇脱险命令,可能会失去成功控制海难的机会,使军队财产蒙受巨大损失;反之,如果过晚下达弃艇脱险命令或错误选择在舱室等待救援,艇员可能丧失离艇可能性,生命安全得不到保障。因此,为了最大程度保证潜艇艇员成功脱险,指挥员需要根据实际情况准确、快速地作出弃艇脱险的决策。
理想情况下,指挥员可以获得多方面的失事信息(如海洋环境要素、舱室环境要素、装备状态要素、人员状态要素等),并依据这些信息和相应的计算分析模型进行弃艇脱险与待援决策。但是,在失事状态下,往往得不到需要的足够信息或信息不明朗,这时,指挥员往往根据直觉和个人经验来处理,难免考虑不周、思维出现混乱而作出错误决策,尽管广大指战员和科研人员对于弃艇脱险决策的重要性早有认识,由于决策的目标环境和决策者十分特殊,对于该问题的研究还相当缺乏。
层次分析法(Analytic Hierarchy Process,AHP)是美国运筹学家T.L.Saty教授于20世纪70年代初期提出的一种简便、灵活而又实用的多准则决策方法,它是一种定性和定量相结合的、系统化、层次化的分析方法,它把一个复杂问题分解成若干组成因素,并按支配关系形成层次结构,然后应用两两比较的方法确定决策方案的相对重要性。该方法尤其适合于对决策结果难于直接准确计量的场合。本文针对弃艇脱险这种信息量化不确定、多因素、多目标的现场决策问题,采用层次分析理论进行了辅助建模和探索。
1 模型探讨
在失事潜艇的弃艇脱险问题的决策分析中,指挥员会面临海损程度、外界环境、舱室大气环境、舱内备品、人员心理状态、训练素质、设备状态等诸多因素,这些因素层面不同、互相关联、相互制约,共同对指挥员产生心理影响。下面,针对这样一个纷繁复杂、缺少定量数据的系统,以弃艇脱险决策为目标进行决策建模探讨。依照层次分析法理论,建模过程大体上可按下面4个步骤进行。
1.1 递阶层次结构的建立
应用AHP分析决策问题时,首先要把问题条理化、层次化,构造出一个有层次的结构模型,在这个模型下,复杂问题被分解为元素的组成部分,这些元素又按其属性及关系形成若干层次,上一层次的元素作为准则对下一层次有关元素起支配作用。通过对失事潜艇的脱险决策目标的系统分析,潜艇失事状态下指挥员需要在3项决策策略(立即弃艇C1、择机弃艇C2、舱室待援C3)间作出最佳选择。而影响目标决策的因素主要有8个方面,本着快速、简洁、实用的原则,本文建立如图1所示的3层次结构模型,目标层A是需要决策的问题,即本文探讨解决的问题,对该问题的解决有赖于对准则层B中8个方面因素的综合考虑,而方案层C则是解决目标A的可用候选方法,显然,不同的失事事故中,准则层B的各个因素对方案层C中有不同的影响程度。
1.2 构造判断矩阵
在建立层次结构以后,上下层元素间的隶属关系就被确定了。假定上层元素为V,所支配的下一层次的元素为u1,u2,…,un,接下来需要确定下层次各元素对于V的相对重要性(权重)。由于对于本文探讨的问题,下层次各元素u1,u2,…,un对于V的重要性无法直接定量表示,需要寻找适当的方法导出它们的权重,为此,本文依据图1建立的递阶层次结构,采用Saty等人用实验方法制定的准则去反复比较2个候选方法相对上层目标的相对重要性。由此,得到准则层两两比较矩阵(见表1)和8个方案层两两比较矩阵(见表2)。
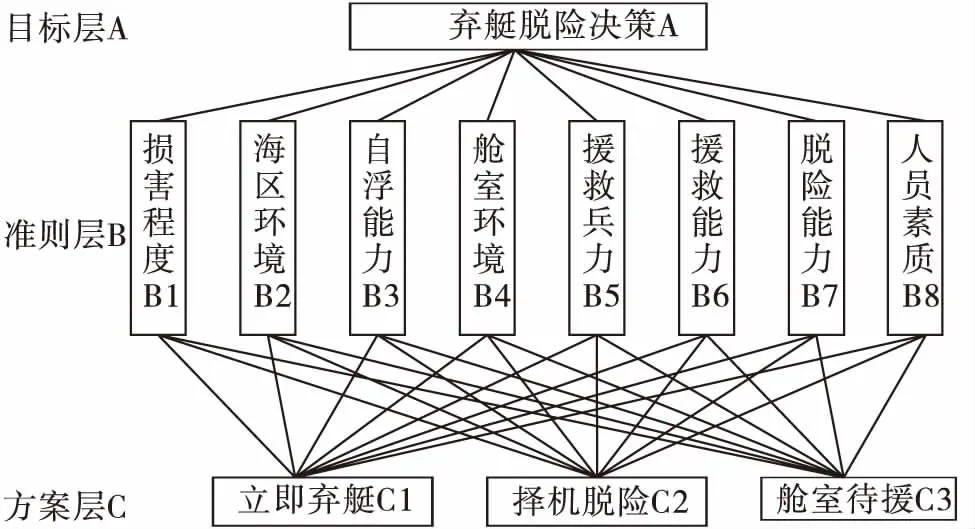
图1 问题的层次结构示意图
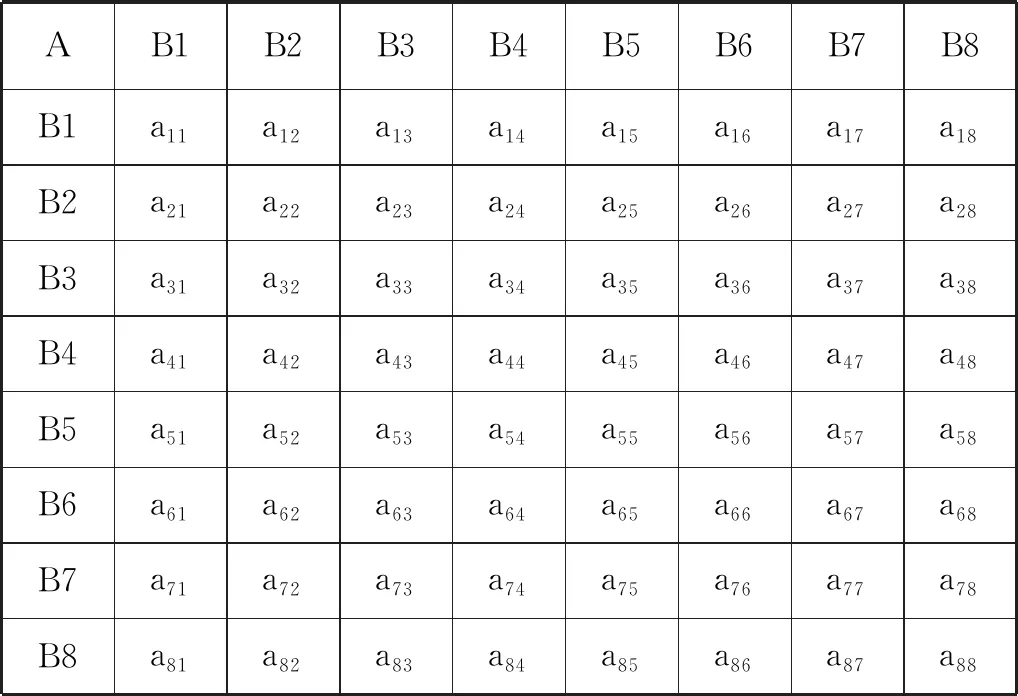
表1 准则层矩阵
式中:aij——纵列因子Bi与横列因子Bj相比较的结果,见表2。
表2方案层矩阵
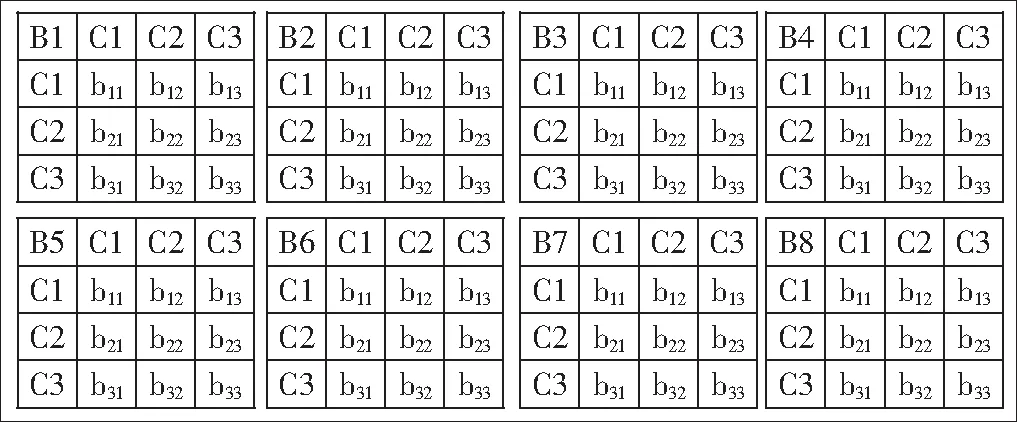
两两比较时使用的比较准则如表3所示。

表3 比较准则
1.3 层次单排序及一致性检验
获得了判断矩阵后,计算矩阵对应于最大特征值λmax的特征向量W,经归一化后即为同一层次相应因素对于上一层次某因素相对重要性的排序权值,这一过程称为层次单排序。通过两两成对比较得到的判断矩阵不一定满足矩阵的一致性条件,需要对判断矩阵进行一致性检验,步骤如下:
计算一致性指标CI
先计算矩阵的最大特征根λmax,然后计算CI:
查找相应的平均随机一致性指标RI。对n=1,…,9,Saaty给出了RI的标准值(见表4)。

表4 RI的标准值
计算一致性比例CR
当CR<0.10时,认为判断矩阵的一致性是可以接受的,否则应对判断矩阵作适当修正,然后重复进行a~c步,直至CR<0.10。
1.4 层次总排序及一致性检验
上面我们得到的是一组元素对其上一层中某元素的权重向量。我们最终要得到最低层中各救生策略(C1、C2、C3)元素对于目标A的排序权重,从而进行策略选择。
总排序权重的获得需要自上而下地将单准则下的权重进行合成。计算方法如下:
设上一层次(A层)包含A1,…,Am共m个因素,它们的层次单排序权重分别为a1,…,am。又设其后的下一层次(B层)包含n个因素B1,…,Bn,它们关于Aj的层次单排序权重分别为b1j,…,bnj(当Bi与Aj无关联时,bij=0)。按照下式计算B层中各因素关于总目标的层次总排序权重b1,…,bn,即:
其中,i=1,…,n
对层次总排序也需要作一致性检验,检验仍象层次总排序那样由高层到低层逐层进行。设B层中与Aj相关的因素的成对比较判断矩阵在单排序中经一致性检验,求得单排序一致性指标为CI(j),(j=1,…,m),相应的平均随机一致性指标为RI(j)、CI(j)、RI(j)已在层次单排序时求得),则B层总排序随机一致性比例为
当CR<0.10时,认为层次总排序结果具有较满意的一致性并接受该分析结果。
2 验算与结论
对上述决策模型,我们进行了试验性质的计算机软件编程和测试(见图2)。

图2 模型编程验算
在调试正确的基础上,提供给部分人员试用,通过对上述模型的编程使用与验算,得到如下结论。
1)利用层次分析法构建弃艇脱险辅助决策模型,可以实现对问题的快速决策的功能,尤其在信息不完备条件下,为潜艇指挥员提供一个简便、灵活而又实用的辅助决策手段和工具。
2)层次分析法受到人的主观价值观、主观判断、主观意向等因素的影响较大,并不能够代替人工思维,能够去除人工思维中的不确定性和混乱性,使得结果更趋合理和可靠。
3)上述层次结构中的准则层可以进一步扩展,得到更加合理的决策结果。
