耦合矩阵故障条件下非线性复杂网络系统的稳定性分析

翟春艳，孟祥雪，王国良

（辽宁石油化工大学信息与控制工程学院，辽宁抚顺113001）

随着时代不断的进步与发展，很多事情都可以运用复杂网络进行处理[1-3]。生活中的网络通常指的是互联网、通信网和人际网等。本文所研究的复杂网络与上述提到的是截然不同的，是指具有高度复杂性的网络。20世纪80年代，复杂性科学理念被提出，在复杂系统中不能用简单的方式去解决问题，并且部分系统还具有自适应性和不确定性等因素。其复杂性可以从以下几方面进行解释：系统结构的复杂性、网络节点的进化度、节点之间连接的多样性和多种复杂网络之间的相融合。复杂网络有同步控制[4-7]、结构控制[8-9]、牵制控制[10-11]、自适应控制[12-13]等多种控制方式。一般情况下，经验证稳定的复杂网络系统才能被应用到实际的工程中。复杂网络系统的稳定性是指在一个正常运转的网络系统中，当系统受到非人为干扰的情况后，本身可以恢复到稳定的过程。通常使用李雅普诺夫（Lyapunov）稳定性理论[14-17]判断系统的稳定性。

本文以具有非线性的复杂网络[18]系统作为研究对象，运用Lyapunov稳定性理论的方法分析了系统的稳定性问题。研究过程中考虑了复杂网络系统的时间节点、拓扑结构[19-21]和矩阵耦合性等因素，为了在研究过程中减小运算过程的复杂程度，将系统模型转化为Kronecker积的形式进行等价描述。针对子系统的切换时刻，提出将其转化为离散化形式的方法，使系统渐近稳定。最后通过仿真算例进一步验证提出方法的有效性。

1 非线性系统问题描述

考虑由如下N个非线性节点组成的复杂网络系统为：

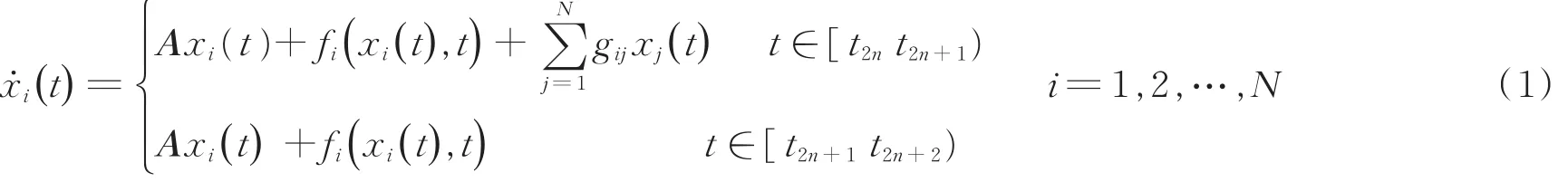
令G=(gij)N×N是的和，表示复杂网络耦合矩阵，代表复杂网络的拓扑结构。特别地，系统（1）的时间端点定义为：

（1）在区间[t2n,t2n+1)的驻留时间τ=t2n+1-t2n,n∈N；

（2）在区间[t2n+1,t2n+2)的驻留时间φ=t2n+2-t2n+1,n∈N。

定义α(t)为：

变量α(t)表示网络中的关联存在与否，并可以将系统（1）统一表示为：

基于Kronecker积，式（3）等价于：

假设1存在大于零的常数ρ，系统（4）中的非线性满足：

定义1设系统（4）渐近稳定，如果系统（4）的解满足：

引理1对于任意矩阵有：

2 主要结果

定理1在假设1条件下，称非线性复杂网络系统（1）是渐近稳定的，如果对给定的参数ωˉi＞ 0、-ωi＞ 0,i=1,2，存在矩阵Pi＞ 0，i=1,2且满足：

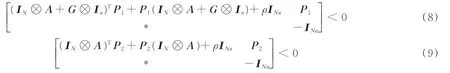
式中，*为任意矩阵。

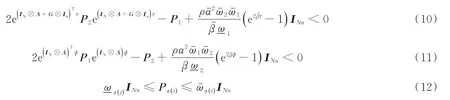
其中，、ˉ与α、β分别针对矩(ΙN⊗A+G⊗Ιn)与(ΙN⊗A)满足引理 1。

证明针对系统（4）定义Lyapunov函数为：

式（13）可以改写为：

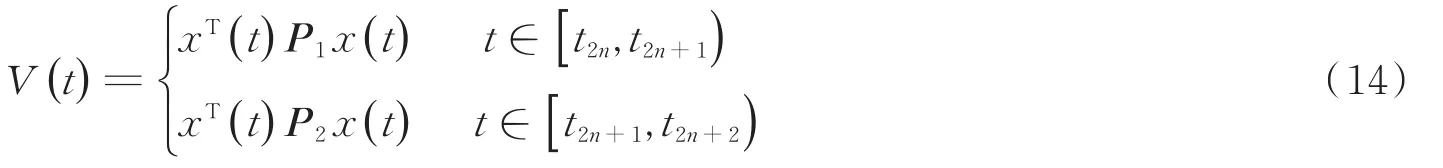
对式（14）进行求导得：

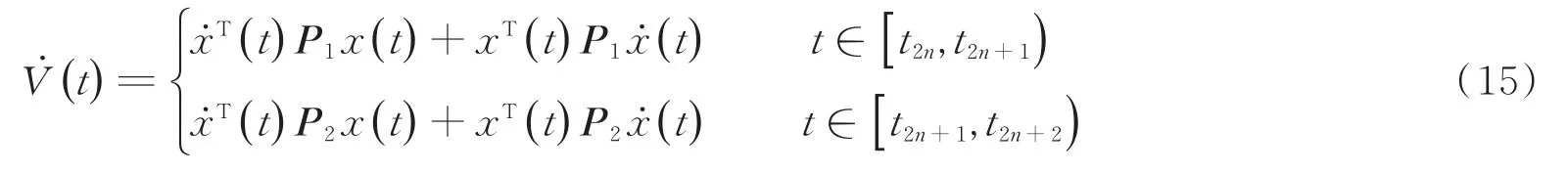
当t∈ [t2n,t2n+1)时，α(t)=1，根据Schur补引理和条件（8）有：

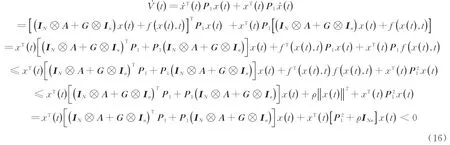
同理，当t∈[t2n+1,t2n+2)，α(t)=0，根据Schur补引理和条件（9）有：

由此可知上述子系统的能量函数V(t)=xT(t)Pσ(t)x(t)在[t2n,t2n+1)和[t2n+1,t2n+2)区间内分别单调递减。当t∈[t2n,t2n+1)时，即α(t)=1，系统（4）变为：

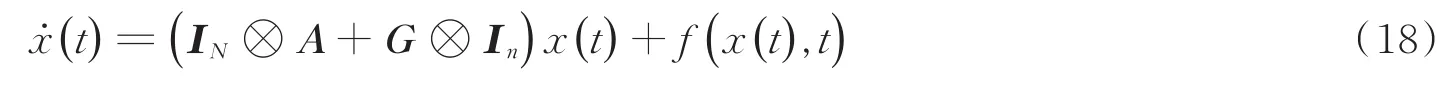
其解为：

特别地，当t=t2n+1时有：

将式（20）简记为：

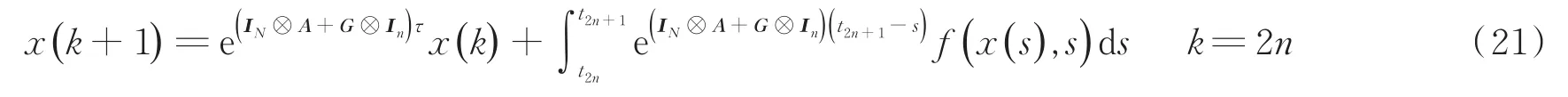
同理，当t∈[t2n+1,t2n+2

)时，即α(t)=0，系统（4）可以表示为：

相应解为：

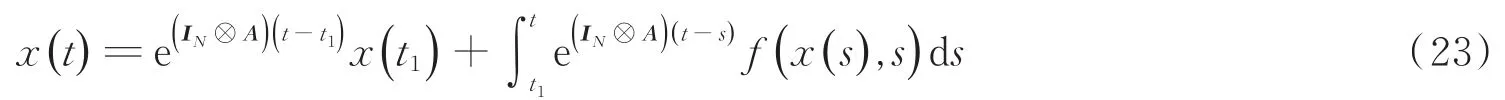
其中，当t=t2n+2时根据式（23）得：

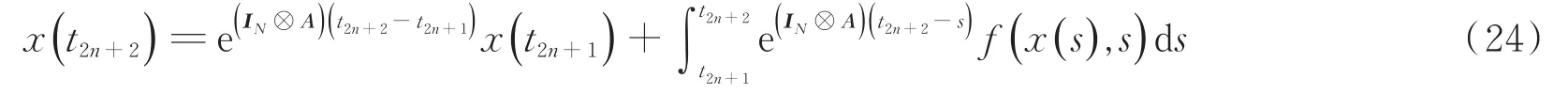
简记为：

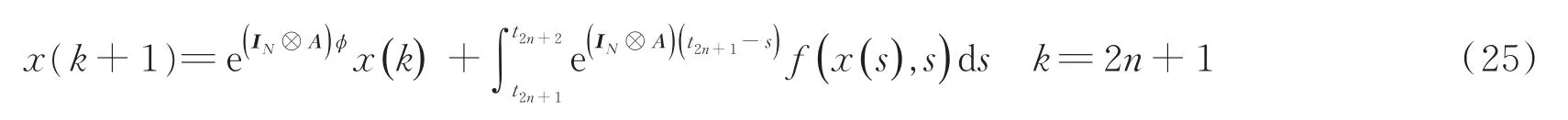
根据式（21）和式（25）得：

对上述系统定义如下Lyapunov函数：

从而

当k=2n时，τ=t2n+1-t2n,n∈N，有：

基于条件（12），其中交叉项处理为：

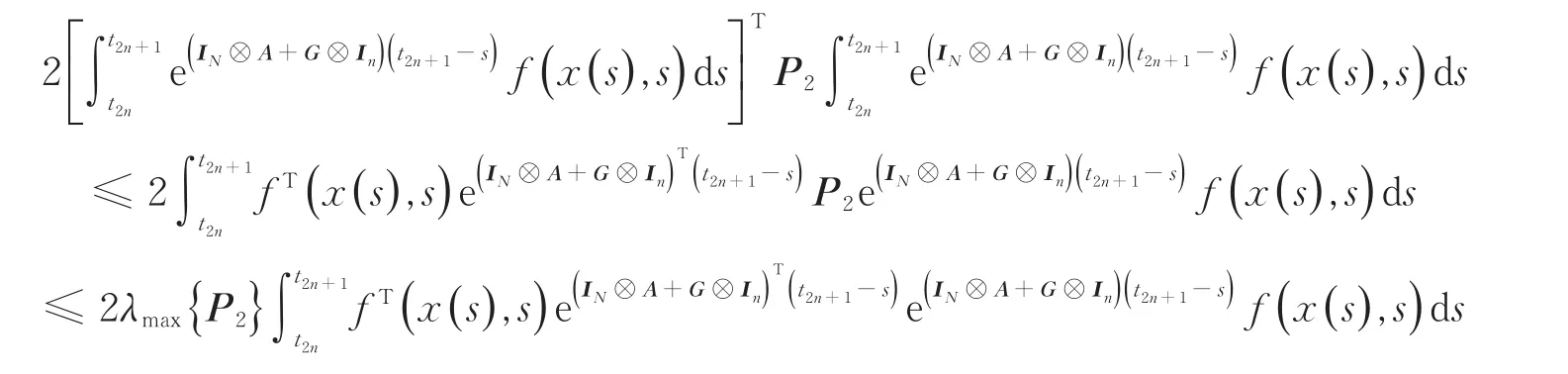
因此，

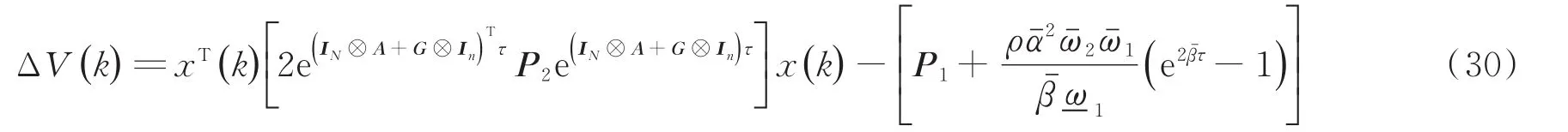
当k=2n+1时，φ=t2n+2-t2n+1,n∈N，可得：

同理，其中的交叉项处理为：

因此，

根据式（30）和式（32）得：

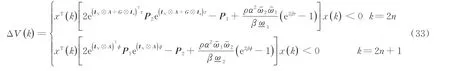
基于非线性节点组成的复杂网络系统式（5），在非线性项等于零时，线性复杂网络系统为：

基于Kronecker积式（35）等价于：

推论1线性复杂网络系统（35）渐近稳定，如果对给定的参数ωˉi＞ 0、-ωi＞ 0，i=1,2，存在矩阵Pi＞0,i=1,2且满足：

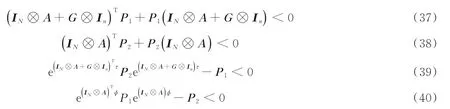
以上条件的线性复杂网络系统稳定，其中式（39）和式（40）中τ=t2n+1-t2n,n∈N，φ=t2n+2-t2n+1,n∈N。

3 仿真案例

为方便研究，考虑5个节点的复杂网络系统，根据式（1）将系统矩阵A和网络耦合矩阵G的参数分别描述为：

根据引理1，计算得β=2.458 2和α=-3.256 7，其中根据式（5）进行计算得ρ=0.16。系统状态x(t)的响应曲线的仿真结果如图1所示。仿真结果表明，复杂网络系统是稳定的。

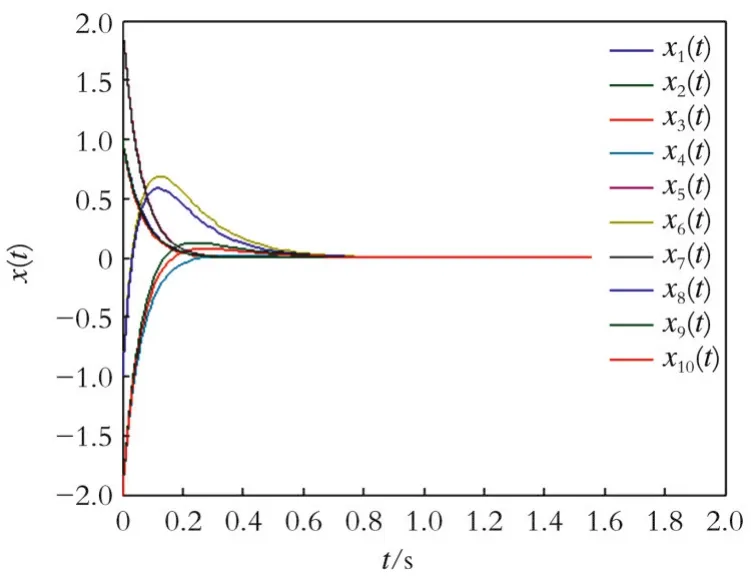
图1 系统状态x(t)的响应曲线的仿真结果

复杂网络系统α(t)的响应曲线的仿真结果如图2所示。其中，τ=1、φ=1。从图2可以看出，α(t)在奇数区间为1，偶数区间为0。

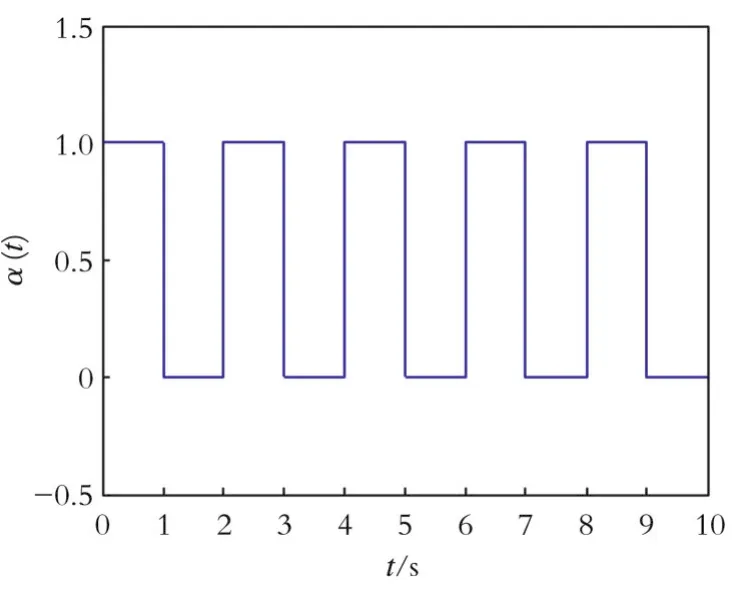
图2 复杂网络系统α(t)的响应曲线的仿真结果

4 结 论

研究了非线性复杂网络系统的稳定性问题，在大规模复杂网络中通过设计不同节点组成的网路耦合矩阵解决其网络问题。针对非线性的复杂网络系统，选取合适的Lyapunov函数分析系统的稳定性并进行严谨的运算，得到了非线性复杂网络系统稳定性的充分条件,并且将该方法推广到线性复杂网络的稳定性分析中。最后通过数值例子进行仿真，进一步验证了所提出方法的适用性和有效性。