基于粒子滤波的运动目标光电定位仿真研究

秦 川，陶 忠，桑 蔚，张 鹏，海云波，梅甫麟

（西安应用光学研究所，陕西 西安 710065）

引言

机载光电目标定位任务主要由载机、光电转塔和GPS/惯导（INS）三大系统组成。其中GPS/INS提供载机的经纬高信息和姿态信息，光电转塔完成对目标的搜索、捕获、定位和跟踪等功能，结合传感器本身参数即可实现对海平面目标的无源定位任务；若结合安装于光电转塔内的激光测距机测量信息，则可实现三维空间目标的有源定位任务。

然而，GPS 测量载机经纬高存在误差，惯导系统（INS）测量载机姿态也存在误差，光电转塔视轴也存在抖动，目标横向与纵向像素的视频判别并非绝对准确，对于静止目标，通过多次测量取均值的方法可极大减小上述测量噪声的影响[1]。但是对于运动目标，除采用Kalman 滤波算法[2-3]外，也可采用粒子滤波算法。该算法既可应用于线性系统，还适用于非线性系统。

文献[1]主要对海面目标光电无源定位原理进行了仿真，分析了定位精度；文献[2]针对有源定位模型讨论了机载光电吊舱目标定位技术，但其选择的状态量和观测量不利于线性Kalman 模型，计算较复杂；文献[3]较早讨论了Kalman 滤波算法在目标定位中的应用，但选取的状态量和观测量同样也不利于简化模型；文献[4]和[5]主要讨论粒子滤波算法在目标跟踪中的应用；文献[6]讨论了粒子滤波在光电目标定位中的应用，但与本文的主要区别是该文针对光电目标定位为地面基站对空中飞机等目标的定位，定位模型不一样；文献[7]主要对静止目标建立粒子滤波模型，用在移动无线电检测车对干扰源的定位实践中；文献[8]将粒子滤波算法用来处理原始测量值，用于基站对移动目标的定位。

本文将目标定位算法与粒子滤波算法相结合，针对载机平台光电转塔对海面（地面）移动（静止）目标定位需求，从理论上推导了计算公式及初值和参数的选取方法,用只含测量噪声,添加测量及目标运动噪声时的海面运动目标光电无源定位仿真案例验证粒子滤波算法的有效性。从噪声强度对滤波效果的影响、滤波参数选择对滤波效果的影响、目标运动方式对滤波跟随性的影响、重采样算法对滤波效果的影响等几个方面进行了探讨。本文的理论分析及仿真方法对于目标定位研究具有一定指导意义。

1 粒子滤波无源目标定位算法

粒子滤波是一种基于Monte Carlo 仿真的近似Bayes 滤波算法。其核心思想是，用一些离散随机采样点来近似系统随机变量的概率密度函数，以样本均值代替积分运算，从而获得状态的最小方差估计[9]。

1.1 目标运动的状态及观测模型

假设海面上目标k节点的经纬度为（LT(k),BT(k)），经过采样时间间隔t，目标运动到k+1 节点，其经纬度为（LT(k+1),BT(k+1)），在较短时间Δt内，假设目标在经纬度平面做匀角速度运动，由海浪及海风引起的随机经度角加速度为ωL(k)、随机纬度角加速度为ωB(k)，则由运动学理论可知：

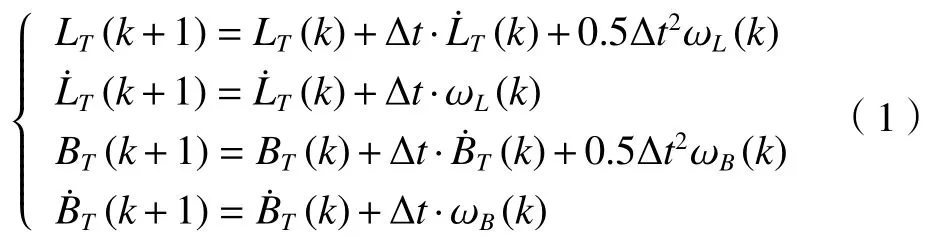
将（1）式写成矩阵形式，即目标的状态方程：

另一方面，载机通过光电转塔对目标进行定位，关心目标的经纬度（LT'(k),BT'(k)），同样假设经度观测定位误差为νL(k)，纬度观测定位误差为νB(k)，则观测方程为

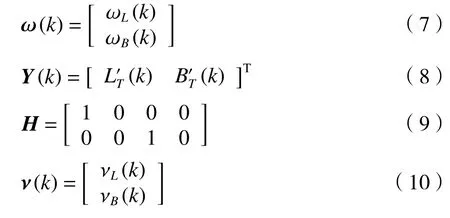
则状态方程和观测方程进一步改写为

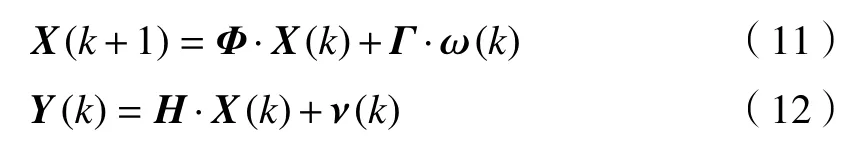
1.2 粒子滤波算法

1.2.1 算法流程

如图1 所示，基于粒子滤波的无源目标定位算法如下：

1)基于初始状态及均值为0 的角加速度噪声ω和角速度噪声V的方差矩阵Q和P，生成样本量为N的粒子群；

2)采用状态方程做状态预测；

3)采用观测方程得观测量；

4)将观测值与测量值进行比较分析，得到归一化权重；

5)根据上述计算得到的权重，对状态预测结果重采样，进行状态更新；

6)从2)～5)循环迭代，并计算每节点粒子状态的平均，作为该节点的均值估计。

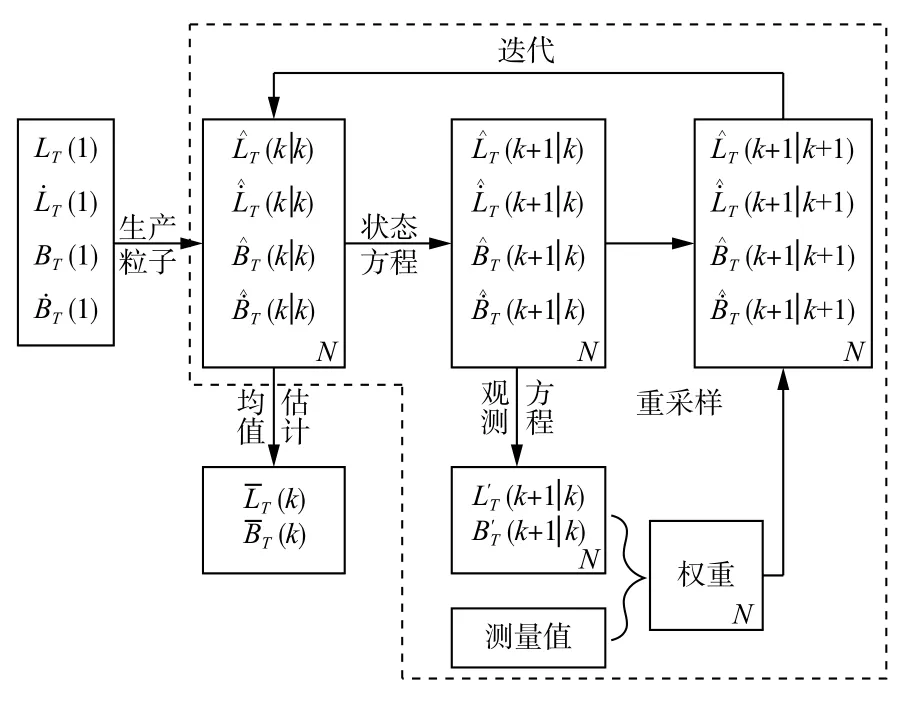
图1 无源目标定位粒子滤波算法流程Fig.1 Flow chart of passive target positioning particle filter algorithm

1.2.2 权重的计算

对于海平面目标，其经纬高的观测值位于(LT'(k+1|k),BT'(k+1|k), 0)，而目标的测量值（即采用载机GPS、惯导、转塔光电码盘等传感器测量的原始数据，经坐标变换后直接得到的目标经纬高值[1]）为（LM(k),BM(k), 0），则由观测噪声ν的方差矩阵采用Gaussian 型概率分布描述，忽略常数项因子，对于每个粒子i，则有[9]：

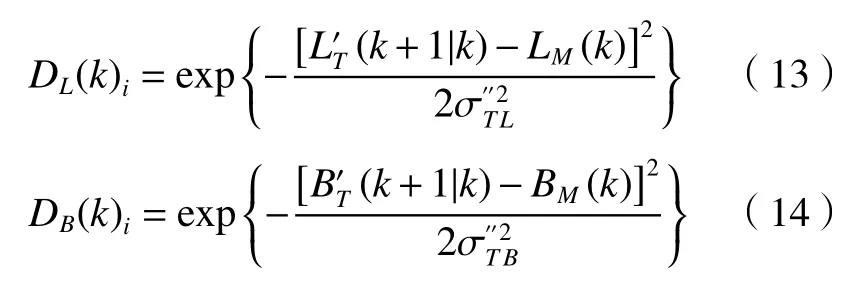
经归一化处理，得到经纬度的权重：

1.2.3 重采样

粒子滤波的“优胜劣汰”主要体现在粒子的复制上，这是通过重采样算法实现，其基本思想是通过对样本重新采样，大量繁殖权重高的粒子，淘汰权值低的粒子，从而抑制退化。常用的重采样算法有随机重采样[10]、多项式重采样[11]、系统重采样[12]、残差重采样等[13]。本文以随机重采样为例进行较详细说明。

1）产生[0,1]上均匀分布随机数组{uj}j=1,2···N，并做升序排列{Uj}j=1,2···N，且Uj≤Uj+1；

2）计算粒子权重累积函数（对经度、纬度都适用，故省略角标L或B）[10]：

3）如果Uj≤W(k)i并且Uj+1＞W(k)i，则将第i个粒子状态复制给j。

1.3 初始状态及参数确立

要使粒子滤波流程图1 运行下去，就需要输入初始状态、角加速度噪声方差、角速度噪声方差、观测噪声方差等参数。以下依次说明：

1）在k=1 节点，利用该时刻的载机参数及转塔参数，采用光电目标定位算法[1]计算该时刻的目标经纬度，目标运动经纬度角速度可取k=2 节点，相比k=1 节点的经度或纬度变化，时间间隔作为估计值，以此作为初始状态，即：

采用相邻两节点来估算角速度误差较大，容易导致滤波计算结果发散，因此可采用前若干节点来估算角速度，然后对后续节点应用粒子滤波算法。

2）对于任意k节点，亦可利用该时刻的载机参数及转塔参数，采用光电目标定位算法计算该时刻的目标经纬度，以此作为测量值。

3）角加速度噪声方差可依据风力大小、海浪大小凭经验估计，下文仿真中先模拟生成若干组目标准确运动轨迹及含噪声各测量量，然后对目标在随机噪声影响下的经度角加速度和纬度角加速度进行统计，计算其方差，即：

4）角速度噪声方差也采用统计方法，计算经度角速度和纬度角速度方差，即：

5）测量噪声方差也采用统计方法，计算经度、纬度与标准值的方差，即：

2 运动目标定位仿真分析

2.1 测量有噪声情形

假设目标初始在（东经108°53′53″，北纬16°12′45″）海平面上，沿北偏东60°以15 节航速运动，传感器视场0.45°×0.25°，分辨率1 920×1 080 像素，载机飞行速度为400 km/h，运动轨迹如图2 所示。即载机在6 000 m 高度先向北平飞，然后逆时针做3/4 圆周盘旋，接着开始向东爬升高度至7 000 m 后平飞，姿态依照飞行航迹相应调整。

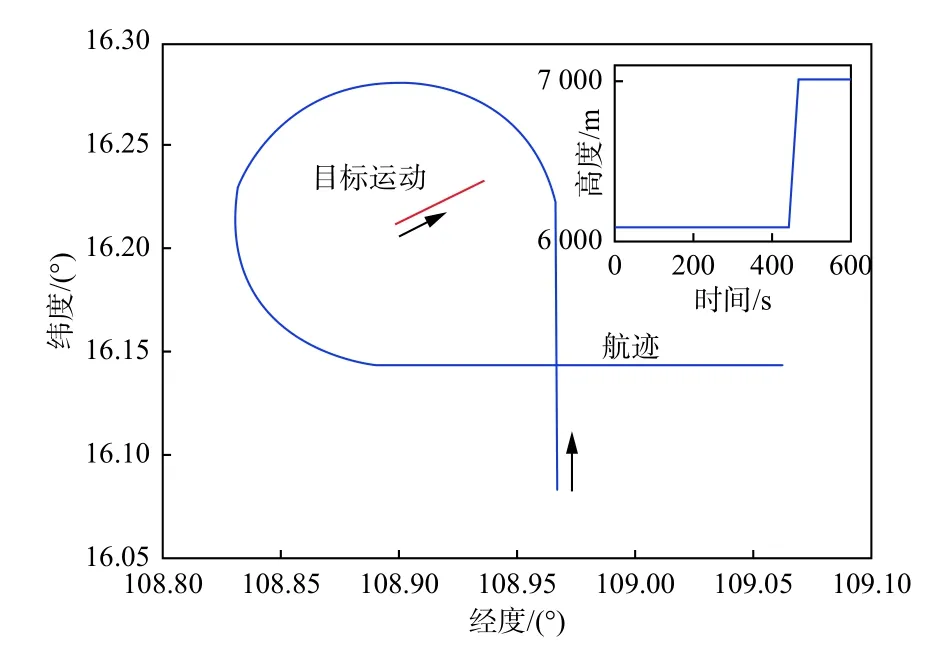
图2 载机航迹与目标运动Fig.2 Aircraft track and target motion

测量误差主要来自GPS 测量载机经纬高的误差、INS 测量载机姿态的误差、光电转塔视轴稳定精度带来的误差、目标横向与纵向像素偏差角的视频判别误差等。上述误差，从统计意义上讲是满足Gaussian 分布的随机误差，其大小如表1 所示。此外，还存在GPS、INS 和光电转塔的安装误差，在载机结构刚性假设下，这三者是固有误差，可通过地面校轴加以减小，本文暂不列入分析。对于传感器视场角和分辨率，也可通过地面检验进行测量，本文暂将其列为固定值。

表1 误差源及其大小Table 1 Error source and its intensity

分析思路如图3 所示。先模拟目标和载机的运动，用目标定位反演算法获得转塔为瞄准目标所转动的方位、俯仰角的准确值，然后对载机GPS数据、INS 数据、转塔方位俯仰角等数据添加噪声，接着用目标定位算法解出目标经纬高的测量值，随后采用本文粒子滤波技术对测量值滤波，其滤波前后结果与初始模拟的目标准确运动轨迹进行比较，用来评价滤波效果。

图3 分析思路Fig.3 Analytical route

在有测量误差情况下，应用粒子滤波算法滤波，目标真实轨迹、测量轨迹和滤波轨迹如图4 所示（因数据点较密，为便于分辨各轨迹，插图中做了局部放大），滤波前后的定位误差如图5 所示，滤波稳定后误差分布如图6 所示。其中抽取50 s，100 s，…，500 s 的相关数据列于表2 所示。从表2可以看出：1）粒子滤波可有效改善受噪声影响的测量数据，其滤波轨迹接近目标真实运动轨迹；2）由于新测量数据对权重的影响，滤波后数据很快趋向真实位置；3）其最大误差由测量轨迹的87.3 m下降到滤波稳定后的20.7 m；4）滤波稳定后的平均误差为4.29 m。

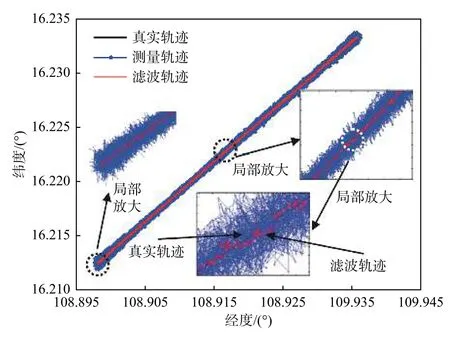
图4 含测量噪声的目标轨迹、测量轨迹与滤波轨迹Fig.4 Target track, located track and filtering track with measurement noise

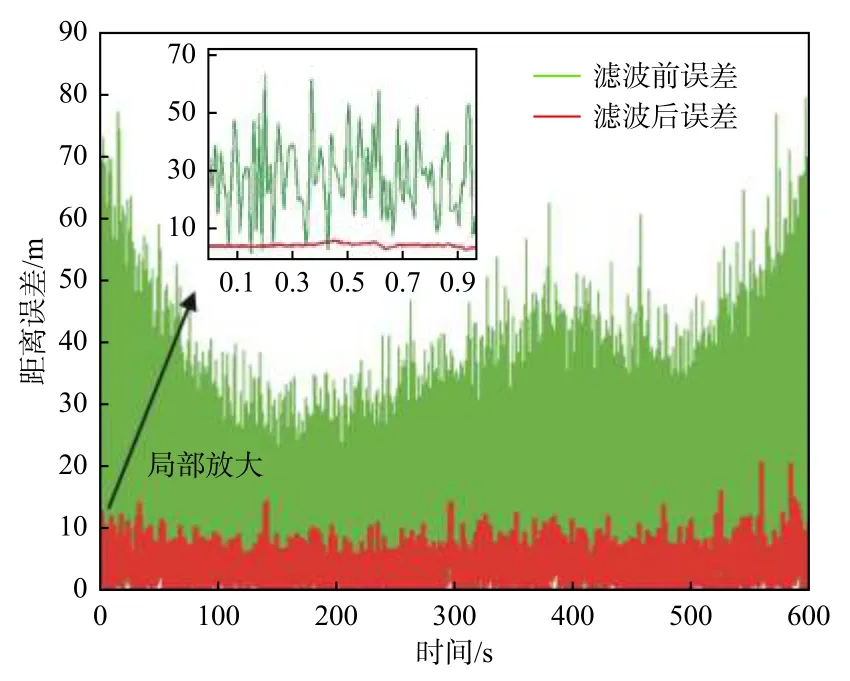
图5 含测量噪声情况下滤波前后的定位误差Fig.5 Positioning error before and after filtering with measurement noise

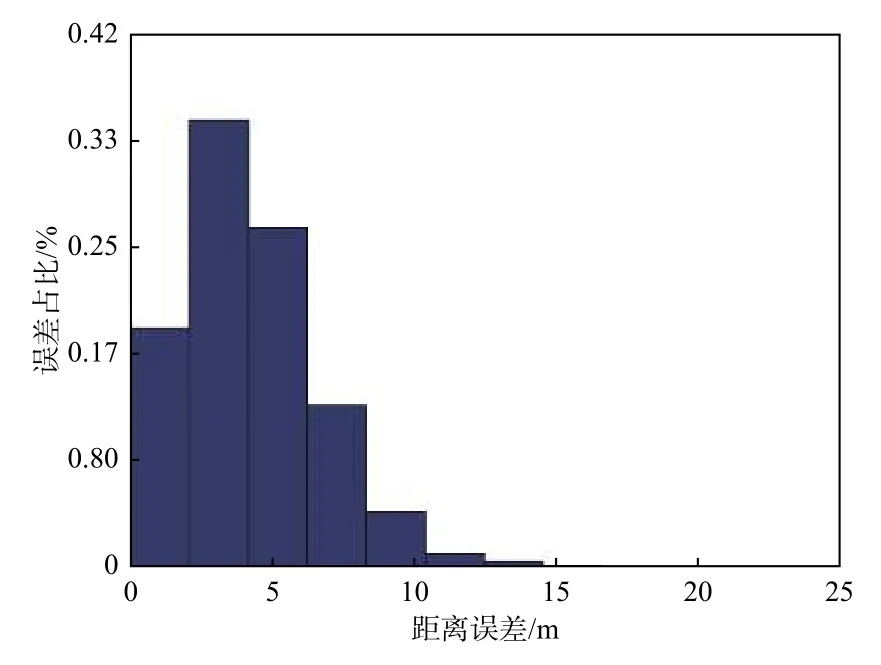
图6 含测量噪声情况下滤波稳定后的定位误差分布Fig.6 Positioning error distribution after filtering stabilization with measurement noise

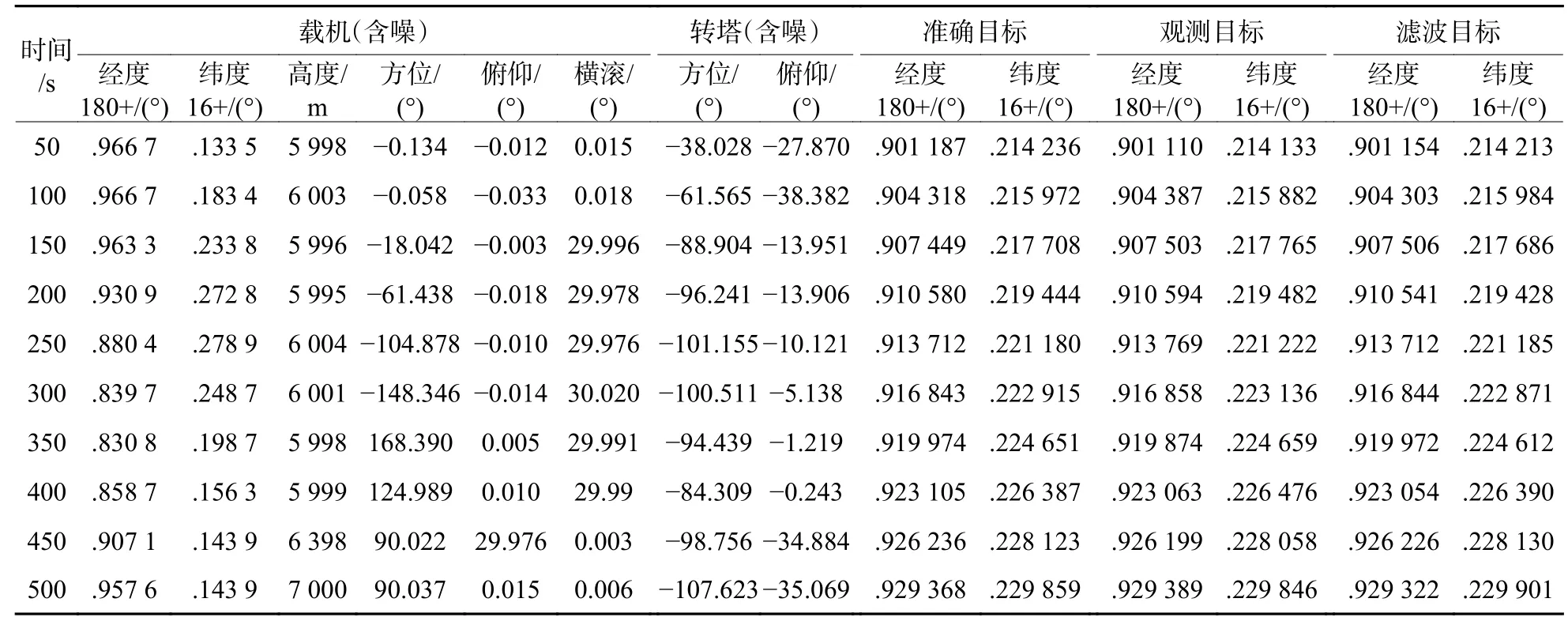
表2 海面运动目标无源定位及粒子滤波相关数据Table 2 Passive positioning and particle filter data of moving targets on the sea

2.2 测量和目标运动均有噪声情形

若目标还受海浪、海风等因素的影响，则可认为目标运动也存在噪声。假设海面目标在经度和纬度方向上运动分别受到幅度为5 m/s 随机噪声扰动，其他仿真条件同上节，对上述仿真案例采用粒子滤波算法进行滤波，结果如图7～图9 所示。可以看出，最大误差由测量轨迹的90.6 m 下降到滤波稳定后的15.4 m，滤波稳定后的平均误差为4.32 m。需要说明的是滤波稳定后的最大误差比上节相应数值还略小，并且图9 的分布比图6 更分散，但数值偏小，这是由于噪声添加的随机性及滤波粒子的随机性引起。

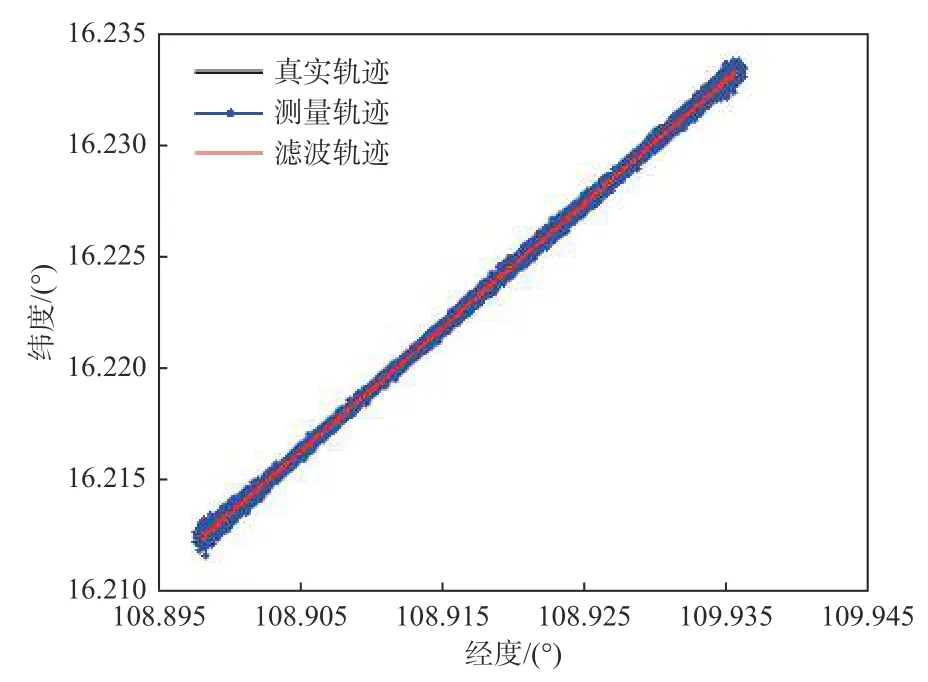
图7 含测量和目标运动噪声的目标轨迹、测量轨迹与滤波轨迹Fig.7 Target track, located track and filter track with measurement and target motion noises

图8 含测量和目标运动噪声情况下滤波前后的定位误差Fig.8 Positioning error before and after filtering with measurement and target motion noises

图9 含测量和目标运动噪声情况下滤波稳定后的定位误差分布Fig.9 Positioning error distribution after filtering stabilization with measurement and target motion noises

3 分析与讨论

3.1 噪声强度对滤波效果的影响

如图9 所示，分3 种情况进行讨论。一是假设测量噪声是上文的2 倍，运动噪声不变（见图10（b））；二是假设运动噪声翻倍，测量噪声不变（见图10（c））；三是测量与运动噪声都翻倍（见图10（d））。为便于对比，将含原始测量和运动噪声的滤波后的定位误差绘于图10（a）中。滤波用的初始值与参数同前面所述相同。从图10 可以看出：1）滤波前最大距离误差、滤波稳定后最大距离误差、平均误差如表3 所示，即滤波效果还是比较明显；2）结合上边所得结果，在假设条件下，相对而言测量噪声对结果的影响大于目标运动噪声；3）噪声与粒子滤波的粒子散布具有一定随机性，因此结果有一定波动，即不一定噪声参数小，结果就小，如表3 中标示出来的3 对数据；4）在一定噪声范围内，滤波效果对初始值和参数的敏感性不大，这也说明算法使用了较合理的初始值和参数，在实际工作中具有鲁棒性。

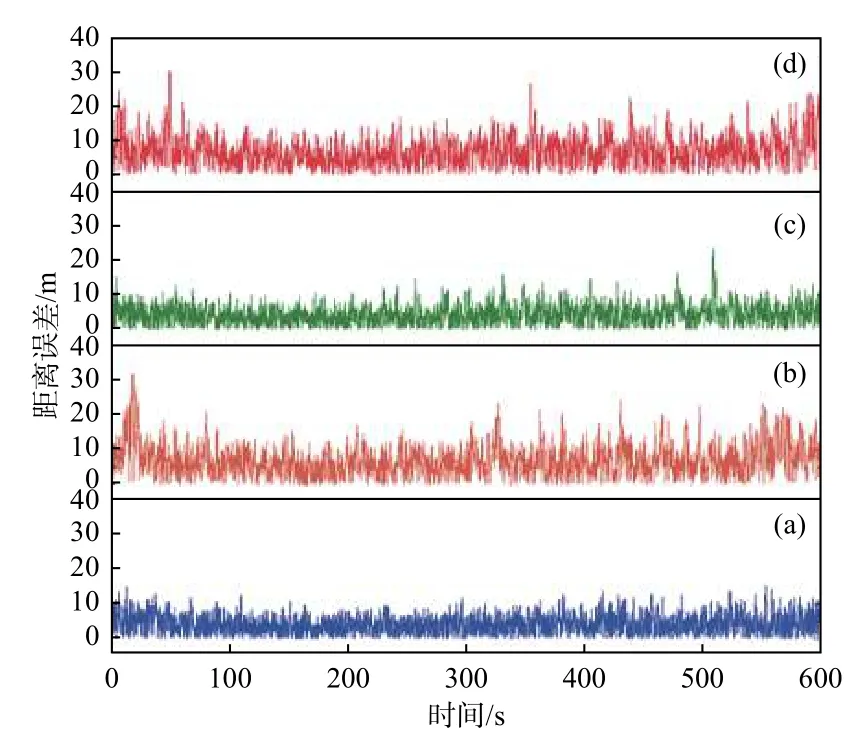
图10 噪声强度对滤波效果的影响Fig.10 Influence of noise intensity on filtering effect

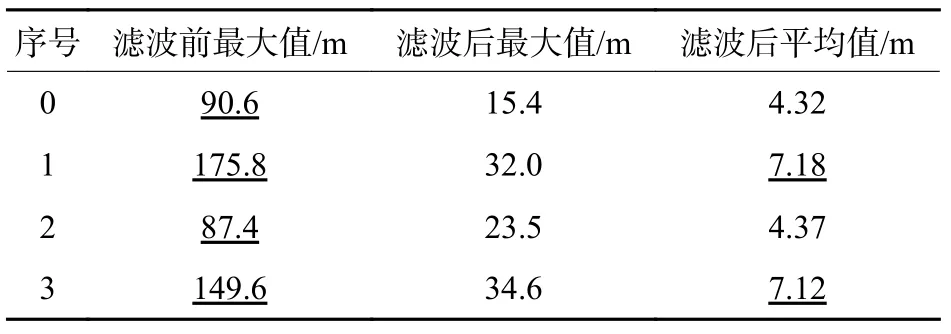
表3 不同噪声强度对滤波效果影响比较Table 3 Comparison of filtering effect with different noise intensities

3.2 初始参数估计对滤波鲁棒性的影响

为了进一步考虑初始参数估计对滤波鲁棒性的影响，在2.2 节基础上，分别将初始值角速度、角加速度噪声方差、角速度噪声方差、测量噪声方差提高2 倍、5 倍，滤波稳定后最大距离误差、平均误差如表4 所示。从表4 可以看出：1）测量噪声方差对前3 项影响略大；2）在一定初始参数估计范围内，滤波效果都收敛到较小数值，这也说明算法使用了较合理的初始值和参数，在实际工作中具有鲁棒性。

3.3 目标运动方式对滤波跟随性的影响

目标运动除受到海浪、海风等外界因素的影响外，假若其自身并非匀速直线运动，比如先按照2.2 节描述方式运动到某处，然后偏转方向继续运动，亦或者目标从一开始就依照弧线运动，亦或者目标基本静止，对于目标观测者来说很难有准确的初始值和参数。假设仍采用上文的预估，此外测量噪声与运动噪声同2.2 节，仿真结果如图11～图13 所示。可以看出，由于权重重采样的作用，滤波曲线基本跟随了目标的运动形态。

表4 初始参数估计对滤波结果影响比较Table 4 Comparison of filtering effect with different initial parameter estimations

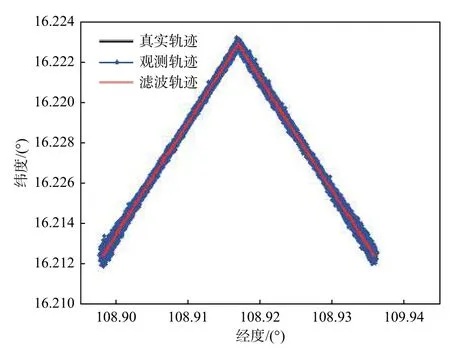
图11 目标折线运动的粒子滤波效果Fig.11 Particle filtering effect of target folded line motion

图12 目标弧线运动的粒子滤波效果Fig.12 Particle filtering effect of target arc motion

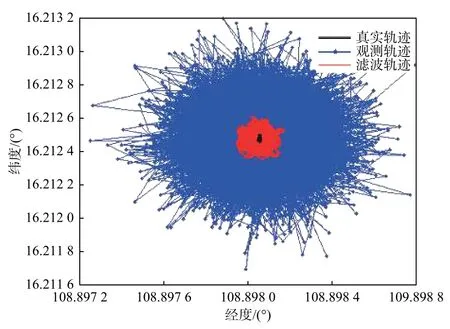
图13 目标基本静止的粒子滤波效果Fig.13 Particle filtering effect of target nearly stationary

3.4 重采样方法对滤波效果的影响

如上文所述，重采样方法主要包括随机重采样、多项式重采样、系统重采样、残差重采样等，前边讨论主要是基于随机重采样方法，现在主要分析采用其他3 种重采样方法的粒子滤波效果。采用2.2 节数据，结果如图14 所示。相同目标运动和测量噪声情况下，采用随机重采样、多项式重采样、系统重采样或残差重采样，粒子滤波稳定后的最大距离误差分别为15.4 m，19.1 m，15.5 m 和15.1 m，平均误差分别为4.32 m，4.44 m，3.09 m 和3.38 m，相对比较接近，无显著性影响。

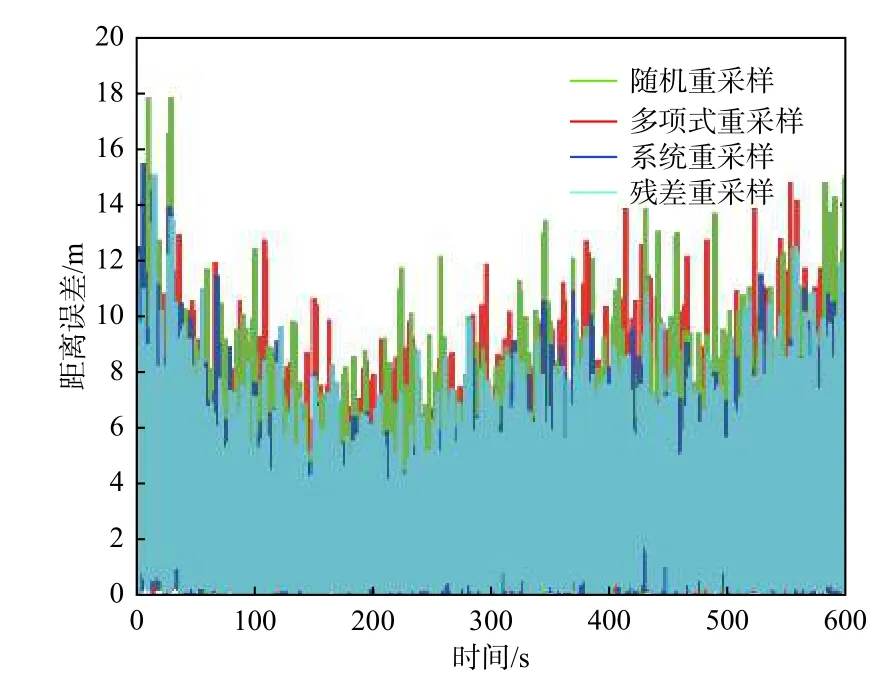
图14 重采样方法对滤波效果的影响Fig.14 Particle filtering effect of target nearly stationary

4 结论

本文采用粒子滤波的方法对含噪声的光电运动目标定位从理论到仿真进行了研究，从理论上推导了粒子滤波算法在光电目标定位中的计算公式，给出初值值和参数选择方法，对测量含噪声情形、测量和目标运动含噪声情形进行了仿真分析，从噪声强度对滤波效果的影响，初始参数估计对滤波鲁棒性的影响，目标运动方式对滤波跟随性的影响，初始值和重采样算法对滤波效果的影响等方面进行了探讨。通过仿真实验得到的结论为：1）粒子滤波可有效用于运动目标光电定位过程，典型情况下，最大误差由没经过滤波时90.6 m降至稳定后的15.4 m，平均误差达到4.32 m；2）粒子滤波算法具有较强鲁棒性，对于有较大噪声，滤波参数选择，目标折转、曲线运动、基本静止情况都适用；3）重采样方法对粒子滤波效果的影响不大。