黄土湿陷特性与物性指标的相关性分析
2020-03-05舒志乐朱世成
舒志乐,朱世成,蒋 洪
(1.西华大学土木建筑与环境学院,四川 成都 610039;2.成都惟尚建筑设计有限公司,四川 成都 610000)
0 引 言
不同于一般粉土与粘性土,高孔隙度和低含水量是天然湿陷性黄土的主要特性。湿陷性是黄土最为重要的工程特性之一,源自其欠压密性和结构性。具有湿陷性的黄土在天然低含水状态下通常表现出高强度性和低压缩性,但当受水浸湿后,天然土体的结构性遭到破坏,强度迅速降低,压缩性变大,在相同的荷重下仍会产生较大附加下沉。建筑在这种具有湿陷性的黄土地基上的建筑物,由于建筑物本身的上下管道漏水、人们的生活用水、大量降雨以及附近渠道蓄水渗漏等都会造成黄土湿陷,使建筑地基产生附加沉陷,其沉陷往往发展迅速,危害巨大。
湿陷性系数是评价黄土湿陷性的重要指标,因而深入研究湿陷性系数,正确评论湿陷性,无论对于理论研究还是工程建设都具有极为重要的意义。苏强[1]通过土体物理力学指标与黄土湿陷系数散点图,分析了各指标与湿陷系数的相关性,并建立了它们之间的回归关系;李论基等[2]在统计分析的基础上,给出了河西走廊黄土物理力学特性一般分布特征,依据影响因子变异性分析和多元线性回归理论,给出了河西走廊地区黄土湿陷系数与黄土物性指标之间的相关性方程;武小鹏等[3]基于数据挖掘技术,提出用多个物理指标综合评价黄土湿陷性的经验公式;宋建等[4]在统计分析的基础上,给出了兰州新区黄土湿陷系数与黄土物性指标之间的经验方程。
许多学者都曾利用统计分析方法得出黄土的湿陷系数与其物性指标间的回归关系式,但因不同地区黄土的天然结构、胶结物含量、孔隙类型不同,得出的回归关系式仅局限于小部分地区。本文利用多元统计分析方法,分析了湿陷系数与其物性指标间的定量关系,得出了由最大湿陷系数、初始饱和度、初始孔隙比计算湿陷系数的二元回归关系式,计算结果与实测值相符,可用于估算黄土的湿陷性,为黄土地区工程建设提高参考。
1 试验概况
试样取自太原地区黄土。经初步湿陷试验比较发现,取自4 m深的土样湿陷性最为明显,因而主要对该深度土样进行增减湿试验。初始含水量下,在标准压力200 kPa下,湿陷系数介于0.03~0.07,属中等湿陷性黄土。土体干容重为14.3 kN/m3试样基本物理特性指标见表1。

表1 黄土增减湿试验土样基本物性指标
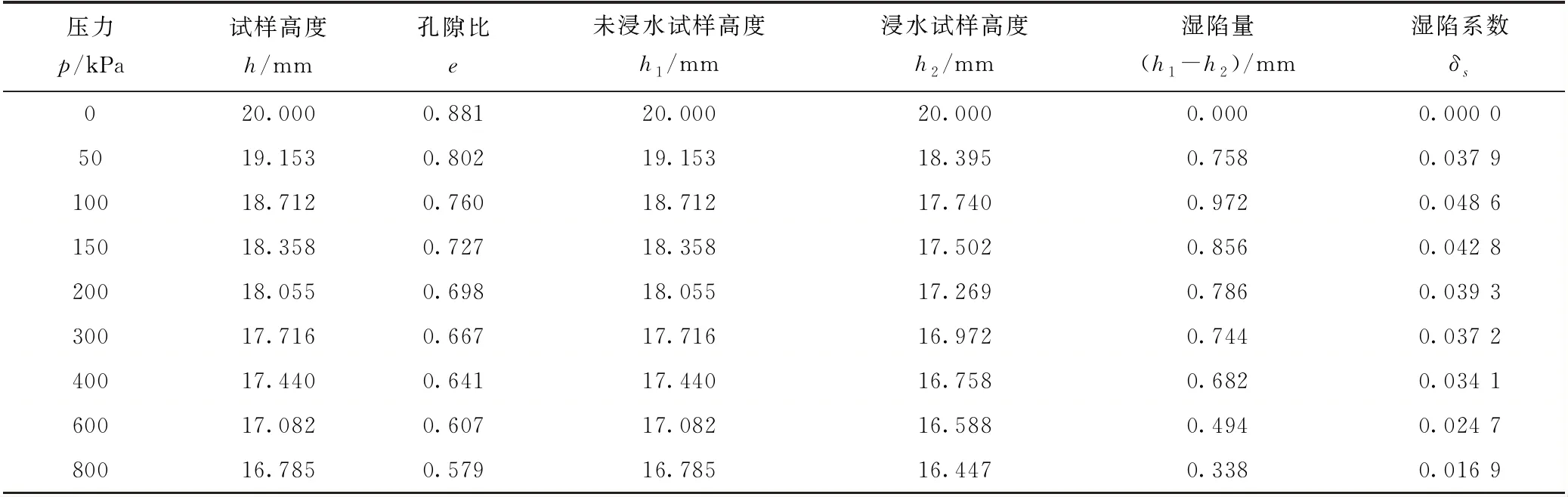
表2 黄土部分湿陷性试验记录
为保证土样的均匀性,对同一土样中所取的环刀试样,其密度差值不大于0.03 g/cm3。所制试样分为5组,1组减湿试样,1组天然含水率试样,3组增湿试样,即烘干含水率为0,天然含水率为14.9%,增湿含水率分别为18.3%、21.6 %、24.9%,对应饱和度分别为0、46%、56%、66%、76%。
(1)增湿试样制备方法。对取好的各环刀试样,提前1 d对试样进行预湿。先用量筒量取所需水量,再用滴管将所需水量分4次缓慢滴入环刀土样,每次滴入总量的1/4,每次操作之间间隔0.5 h,最后将预湿后的环刀试样用保鲜膜包好放入封箱中,静置24 h,使试样内部的水分基本均匀。因增湿后的试件含水率放在封箱中受气温影响,随时间变化含水率会有细微变化,最终含水率以开始试验前测得的试件质量算得的含水率为准。
(2)减湿试样制备方法。将制好的环刀试样在烘箱中烘干8 h以上。黄土的室内湿陷性试验采用双线法测定黄土的湿陷性[5],试验的具体操作方式参照SL 237—1999《土工试验规程》。部分试验数据(天然状态)见表2。将所得数据绘制成图,土样的湿陷系数随压力变化曲线见图1。

图1 湿陷系数随压力变化
2 试验结果与分析
2.1 黄土物性指标的选择
黄土湿陷变形的本质是内因和外因2种因素[6-7],湿陷变形的外因是外力和水,内因是黄土内在的天然结构,外因是诱发因素,内因是决定因素。本文要讨论的回归关系,旨在基于黄土的内因来确定黄土的湿陷系数。影响黄土湿陷的内因很多,由于湿陷性黄土天然低含水状态下具有架空结构,在力和水的共同作用下,架空结构会遭到破坏进而产生湿陷变形。首先,选用为黄土的湿陷变形提供空间条件,造成黄土湿陷性的根本因素,即初始孔隙比e0。其次,骨架颗粒间胶结物的种类和含量也是造成黄土湿陷的内在因素,胶结物中一般对湿陷性贡献较大的是粘土颗粒的含量,而塑性指数IP的变化规律与粘土含量是一致的[8-9]。荷重和水是黄土产生湿陷变形的必要条件,黄土的湿陷系数随初始含水量的变化具有显著不同,选用轴向应力P和初始含水量w0作为影响黄土湿陷变形的物性指标。物性指标选择的简化分析:
(1)土体天然含水量、天然密度、相对密度易于测定,且测量精度高,通过这3个物性指标可以依次换算出土体干重度、孔隙比、饱和度等相关基本物性指标。
(2)塑性指数与胶结物作用密切相关,进而影响黄土的湿陷系数。黄土的湿陷系数通常随塑性指数的增大呈减小趋势,但在同一地区,土体的塑性指数变化不大,且塑性指数的室内测试方法相对繁琐,若用塑性指数判定湿陷系数并不具备显著的实际意义。因而,本文未单独考虑塑性指数对湿陷系数的影响,而将其对湿陷系数的影响宏观考虑在黄土的预测最大湿陷系数中。
(3)饱和度Sr和含水量w0都能反映水对于土样湿陷系数的影响。相比之下,饱和度能直观反映水的体积Vw与孔隙体积间VV的定量关系,且有变化范围。因此,选用饱和度代替含水量。
(4)外力也是黄土湿陷性产生的必要条件,这里为简化计算,将外力作为一个定值考虑,GB 50025—2004《湿陷性黄土地基建筑规范》将10 m以上土层外力200 kPa下的湿陷系数作为黄土湿陷量的计算系数。因此,本文将外力定为200 kPa。
综上考虑,本节主要探究黄土在轴向压力200 kPa作用下,湿陷系数与初始饱和度及孔隙比间的定量关系。从已有的研究中得出普遍性结论,黄土的湿陷系数与初始饱和度呈反比例关系,与初始孔隙比呈正比例关系。
2.2 黄土湿陷系数与物性指标间的回归关系式
2.2.1黄土湿陷系数和初始含水量之间的关系
黄土的变形形式主要有荷重作用下的压缩变形和浸水后产生的湿陷变形。根据大量的试验数据可知,湿陷性黄土在上覆荷重(深度小于10 m的土样,通常为200 kPa)作用下,当初始含水量很低时,浸水后产生的湿陷变形一般较大,甚至大于荷重作用下的压缩变形,对应的湿陷系数大;反之,当初始含水量很高时,浸水后产生的湿陷变形较小,远低于荷重作用下的压缩变形,对应土样的湿陷系数小。由此可见,黄土的湿陷变形和黄土的初始含水量呈现相反的变形规律。
张苏民等[10]、张茂花等[11]及本文等都通过黄土的增减湿试验得出,对于同一土体,黄土的湿陷系数随初始含水量的增大而减小,随初始含水量的减小而增大这一显然结论。含水率与湿陷系数的关系见表3、4、5。拟合结果见图2。图2中,y为湿陷系数;x为初始含水量;R为相关系数,由R2皆趋近于1可知,相关系数极强。

表3 含水率与湿陷系数的关系(张苏民)

表4 含水率与湿陷系数的关系(张茂花)

表5 含水率与湿陷系数的关系(本文)
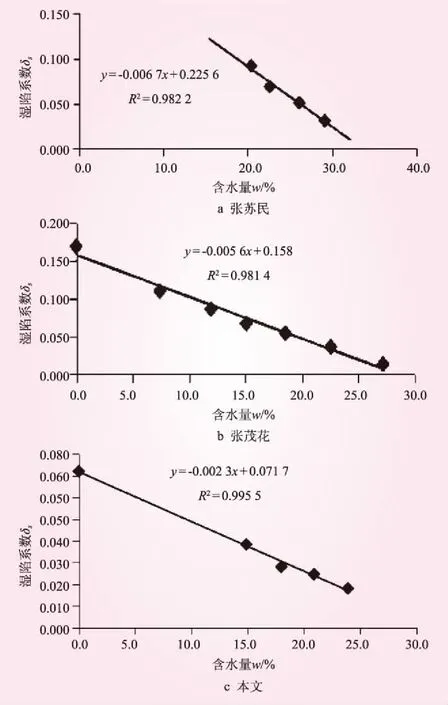
图2 拟合结果
对同一土体,在外力200 kPa下,湿陷系数与初始含水量的定量关系可表示为线性回归方程,即
y=a0x+b0
(1)
式中,a0为回归系数[12];b0为不依赖于x的未知参数,b0值大小受黄土的其他物性指标的影响而变动,整体表现为随初始孔隙比的增大而增大,随土样干重度的增大而减小。
式(2)中x为含水量,其变化量在最小值(烘干含水量wmin=0)到最大值(饱和含水量wmax)之间。对于不同土样,wmax值随孔隙比的增大而增大,不能准确确定。为了统一计算,选用饱和度Sr表示含水量更为合适,相应的回归系数a0转变为a,即
δs=aSr+b0
(2)
黄土的湿陷系数与饱和度为反比例关系,因而值为负数。对同一土体,在200 kPa的轴向压力下,土体的初始含水量由烘干下的0逐渐增加到饱和后的最大含水量,对应饱和度由0增加到100%,其湿陷系数从最大湿陷系数减小至0,且对应近似为线性的。由此可见,对应的值应为最大湿陷系数,且为负值。在实际工程中,若未测得饱和度为0时的最大湿陷系数,可用天然状态孔隙比最大值对应的湿陷系数除以剩余饱和度表示,即
a=-δ0/(1-Sr)
(3)
式中,δ0为天然状态孔隙比最大值时对应的湿陷系数。
2.2.2黄土湿陷系数和初始孔隙比之间的关系
孔隙比同样是影响黄土湿陷系数的主要因素。通过对大量孔隙比不同、其他物性指标相近数据的分析发现,用线性关系、指数关系、多项式表示湿陷系数与孔隙比之间的关系相关系数较高,具有较强的可靠性。有学者根据各地区的试验资料统计得出,黄土的湿陷系数与孔隙比呈正比关系[13]。因此,笔者选用线性回归方程表示黄土的湿陷系数与孔隙比间的关系。在式(2)的基础上,将孔隙比加入考虑因素,式(2)可转化为二元回归关系式,即
δs=a×Sr+b×ε0
(4)
式中,a为与饱和度相关的回归系数;b为与孔隙比相关的回归系数。
黄土的天然孔隙比一般在0.7~1.3之间,湿陷性强的黄土孔隙比相对较大。有学者提出孔隙比小于0.8后,其湿陷系数小于0.015,湿陷性基本消失。笔者通过对孔隙比为0.7的土样进行湿陷试验,天然状态土样含水量较高,湿陷性基本消失,但将土样烘干后,依然具有较为强烈的湿陷性。因此可认为,当土体饱和度为1时,孔隙比为最大值,对应湿陷系数变为0,且两者关系是线性的。由上得a值为最大湿陷系数,即
b=a/emax
(5)
式中,emax为土样天然状态下的最大孔隙比。
将上述得出的二元回归关系式应用于实际工程中,工程实例选用具有很好代表性的湿陷性强烈的兰州黄土,在此引用刘祖典对兰州东岗镇黄土现场浸水试验得出的实测值[6]进行实例验证。其中,湿容重、干容重、天然含水率、实测值均为原始数据,孔隙比、饱和度等为将颗粒比重定为2.69时的代表值[14],公式为
(6)
(7)
计算值为采用公式(4)得出。计算值的计算方法如下:该土样最大孔隙比为1.102,该孔隙比下土样的湿陷系数为0.104,根据反比例线性关系计算该土样对应饱和度为0.231,根据反比例线性关系计算该土样饱和度为0时的最大湿陷系数为0.104/(1-0.231)=0.135,则系数a=-0.135;土样最大孔隙比为1.104,则系数b=0.135/1.102=0.123。代入式(4)中,得到
δs=-0.135×Sr+0.123×e
(8)
将由式(8)算得的计算值和实测值比较,结果见图3。从图3可知,湿陷系数计算结果与实测值相符,可用于估算黄土的湿陷性。

图3 湿陷系数计算值和实测值比较
3 结 语
本文通过黄土土体增减湿试验,并利用多元统计分析方法,分析了黄土的湿陷性系数与物性指标间的关系,得到以下结论:
(1)上覆荷重一定时,随着初始含水量的增加,湿陷系数随之减少;初始含水量不变时,随着上覆荷重的增大,湿陷系数先增加后逐渐减小至最终消失;随初始含水量的增加,峰值压力呈相反变化。
(2)结合各因素间的内在联系,充分考虑实际情况,将对同一地区黄土湿陷系数的影响因素简化至含水量和孔隙比,得出了湿陷系数与含水量和孔隙比的二元回归关系式。
(3)回归关系式具有较强的适用性,在湿陷性强烈的地区,能较为准确地评价黄土的湿陷性。
