基于启动压力梯度的致密油藏非线性渗流模型

马铨峥，杨胜来，王君如，黄 宇

我国致密油探明储量丰富，但由于致密油藏渗透率特低、孔隙结构复杂，导致油藏具有较强的应力敏感和较高的启动压力梯度，流体在孔隙介质中的流动规律不再符合经典的Darcy渗流规律，常规渗流模型不适用于致密油藏。黄延章等[1]认为孔隙介质中的渗流流体包括体相流体与边界流体，且边界流体是导致低渗透储层非线性渗流的主要原因，并建立包含压力梯度的三参数渗流模型。吕成远等[2]采用毛细管平衡法与压差流量法相结合的实验方法，较为完整地测定了低速非达西渗流曲线。邓英尔等[3]、杨清立[4]利用唯象学方法建立了单一函数的非线性渗流模型，但是拟合的数学方程难以反映非线性渗流的影响因素。李永寿等[5]在前人研究的基础上利用油藏压力分度近似表达式的方法研究了超低渗透非线性不稳定渗流特征，并讨论了不同非线性因素对渗流结果的影响等。马勇军等[6]考虑介质变形和启动压力梯度等因素的影响，建立了适用于特低渗透油藏的非线性渗流模型。Y.S.Wu等[7⁃9]通过数值模拟实验研究了非线性渗流对裂缝性、超低渗油藏的动态开发的影响，并建立了相应的渗流模型。

虽然前人对油藏非线性渗流特征进行了大量研究，但是主要针对于低渗、特低渗油藏，且渗流模型不适用于启动压力梯度大且渗透率随油藏压力变化而不断变化的致密油藏[10⁃18]。因此，本文采用新疆吉木萨尔凹陷芦草沟组致密储层天然岩心进行室内岩心驱替实验，在黄延章等[1]提出的非线性渗流模型的基础上，考虑启动压力梯度与渗透率的变化，对其渗流模型进行修正，并根据模型确定了油藏的有效动用压力梯度，从而为致密油藏的合理开发提供理论支持。

1 非线性渗流实验

1.1 实验原理

非线性渗流曲线分为两部分：曲线段和拟线性段，拟线性段的反向延长线与压力梯度轴的交点（不过原点）即为拟启动压力梯度。为了模拟地层中真实情况，实验在定围压下进行，以一定的压力向岩心注入实验流体，测量一定时间内出口端流出液体的体积，从而得到流量的变化；将测定数据的压力梯度⁃流量关系进行线性回归拟合得到直线方程通式为：

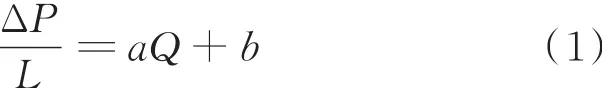
其中，Q 为流量，cm3/s；ΔP 为进出口压力差，MPa；L为岩心长度，cm；a为拟合直线的斜率；b为拟合直线的截距，即为拟启动压力梯度值。

1.2 实验装置

致密油储集启动压力梯度测试实验装置主要由注入系统、温度控制系统以及数据采集系统三部分组成。注入系统主要包括美国生产260D ISCO高精度驱替泵（最大工作压力52.00 MPa）、回压泵、围压泵、中间容器、压力传感器、高压夹持器、液体计量装置等；温度控制系统主要包括恒温箱、温度传感器等，主要作用是确保整个实验过程中系统温度维持恒定，避免温度的变化对实验结果造成影响；数据采集系统主要包括计算机、传感器、A/D转换器等，主要用来采集、记录实验过程中压力、流量以及温度等相应参数的变化。实验装置示意如图1所示。

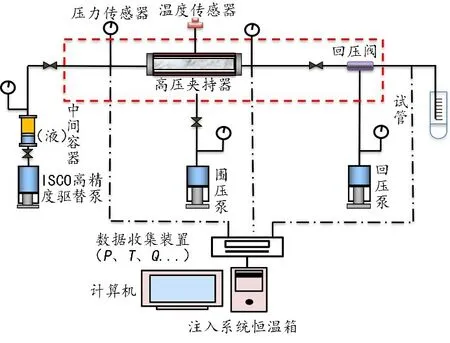
图1 实验装置示意Fig.1 The experimental schematic diagram

1.3 实验材料

实验采用新疆吉木萨尔油田的天然岩心，岩样的基础物性参数见表1。

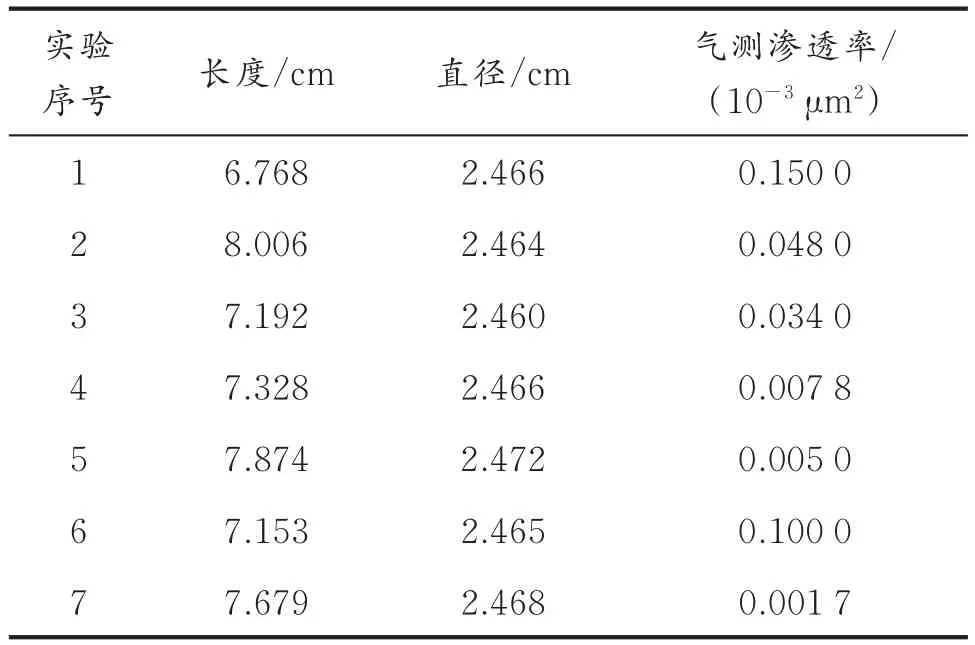
表1 实验岩样基本参数Table 1 Basic parameters of core samples

1.4 实验步骤

①将目标油藏岩心洗油后，测量岩心长度、直径、孔隙度和渗透率等基本物性参数；②按SY/T 5336规定执行[19]，抽真空24 h以上，然后用煤油进行饱和；③在油藏条件下，将饱和后的岩心放入加持器中，然后用煤油进行驱替；根据行业标准进行实验点设计，实验过程中围压保持比上游压力大2.50～3.00 MPa；④在驱替过程中，下游压力设为大气压，逐渐增大上游压力，待下游系统稳定后，测量并记录不同压差下流体产出流量；⑤画出样品的渗流曲线，回归得出岩心的拟启动压力梯度。

1.5 实验结果分析

以样品1为例画出相应岩心的渗流曲线如图2所示。对曲线进行拟合回归得到样品1-5的拟启动压力梯度分别为 0.15、10.03、13.70、42.22、46.23 MPa/m。同时画出拟启动压力梯度随渗透率的变化关系，结果如图3所示。随着渗透率的增大，拟启动压力梯呈幂率形式递减，当渗透率从0.005×10-3μm2增大到 0.150×10-3μm2时，拟启动压力梯度从46.23 MPa/m减小到3.15 MPa/m。实验结果表明，随着致密油藏压力的变化，储层孔隙流体的启动压力梯度不是一成不变的。

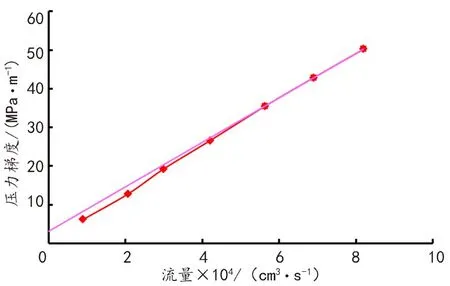
图2 样品1渗流曲线Fig.2 Flow curve of core sample 1

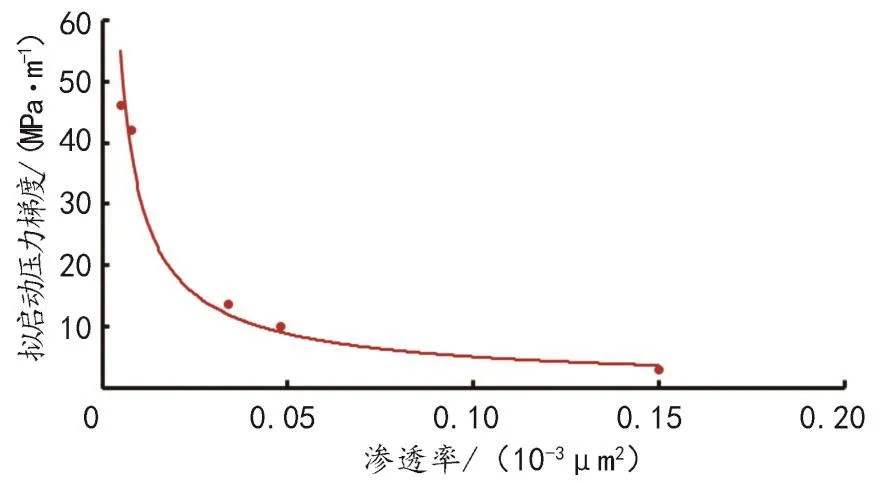
图3 拟启动压力梯度与渗透率的关系Fig.3 Relationship of the pseudo threshold pressure gradient and permeability

2 非线性渗流模型的建立

新提出的致密油藏非线性渗流模型是在低渗非线性渗流模型的基础上，同时考虑致密油藏渗透率不断变化特点，对其进行修正，使新模型适用于致密油藏。

渗透率不变的低渗非线性线性模型：

将实验所得到的渗流速度与压力梯度的关系曲线用二项式进行拟合：

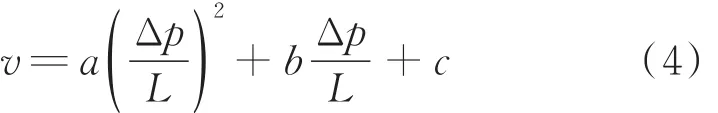
流体在致密油藏中流动，受到岩心、孔道中各种因素的影响，从而导致致密油藏中渗透率随着压力梯度的变化而发生变化，为此，对渗透率进行修正是必要的。

二次函数曲线上任一点的切线表达式为：

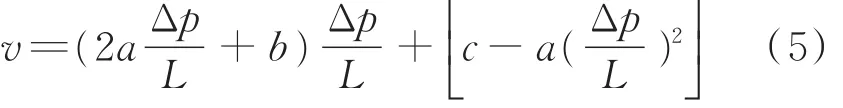
由式（3）和式（5）可得：

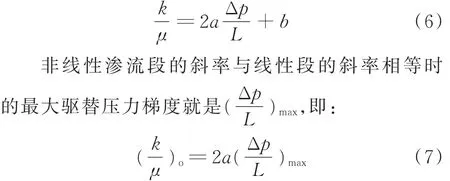
建立样品气测渗透率与最大驱替压力梯度的关系如图4所示。

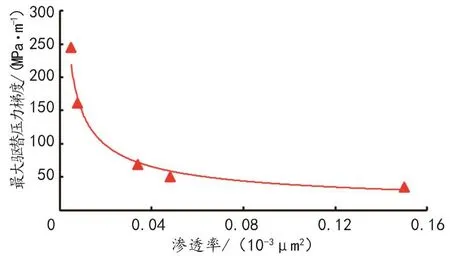
图4 最大启动压力梯度与渗透率的关系Fig.4 Relationship of the maximum threshold pr essur e gradient and permeability

将最大启动压力梯度与渗透率的关系用幂函数拟合可得：

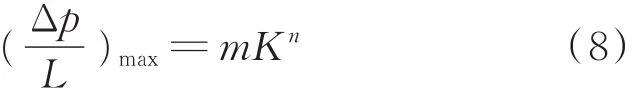
式中，m=0.018 6；n=-0.579。

将式（7）、（8）带入式（2）可得致密油藏非线性渗流模型：

3 模型验证及相关系数的确定

3.1 非线性渗流系数

非线性渗流系数确定如下所示：

式中，a、b、λa、λb、λc值为方程中的相应参数，可以做出参数图版，供直接查用，如图5所示。

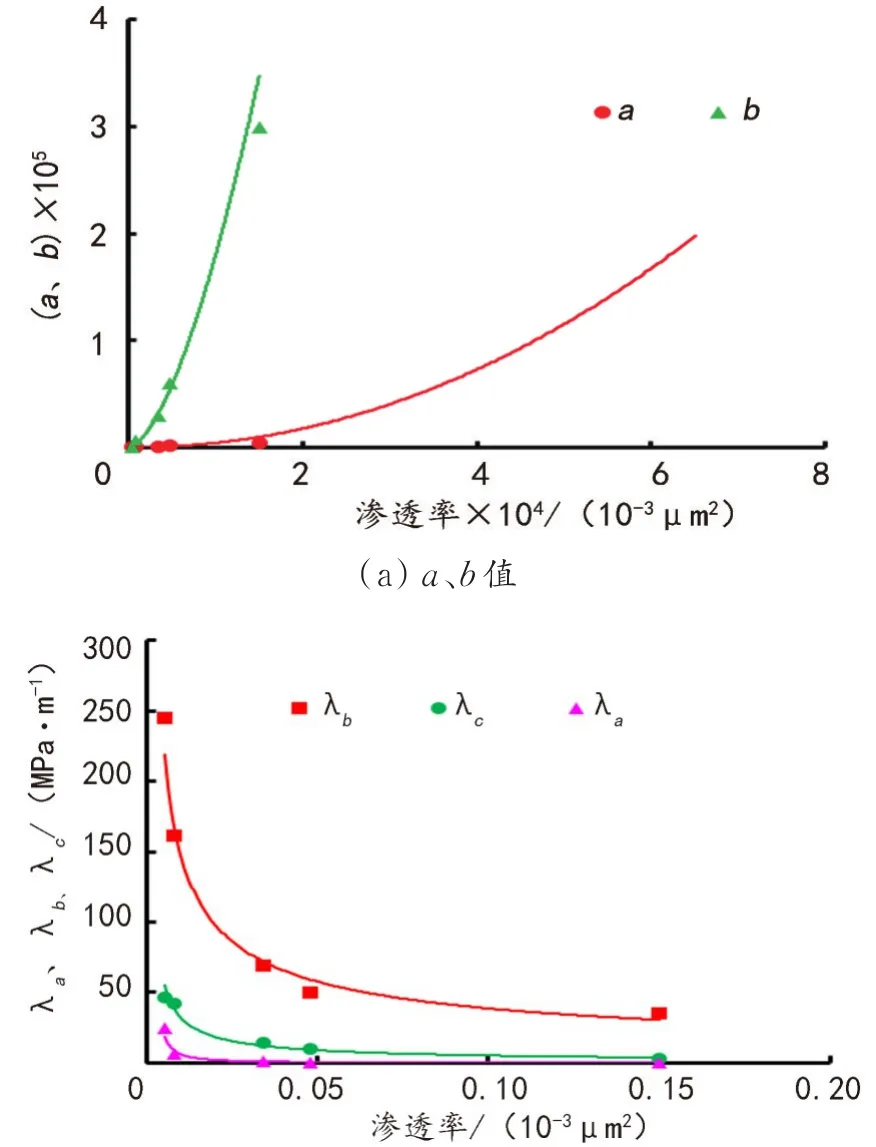
图 5 不同样品的a、b、λa、λb、λc值Fig.5 a、b、λa、λb、λc value of different samples

由图5拟合可得到各参数方程，即：

将式（12）—（15）带入式（9）可得致密油藏非线性渗流模型：

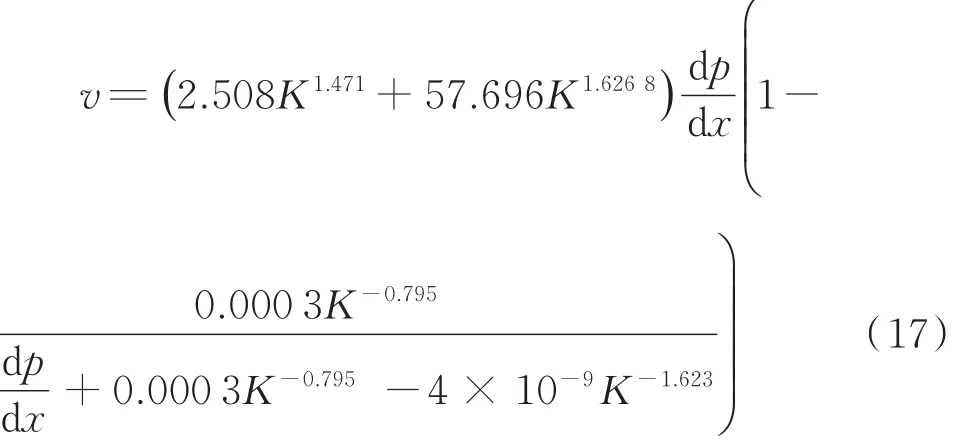
3.2 模型验证

根据所得新模型计算出样品的渗流曲线，与真实测得的样品6和样品7渗流曲线进行对比分析，并进行误差分析，结果如图6所示。

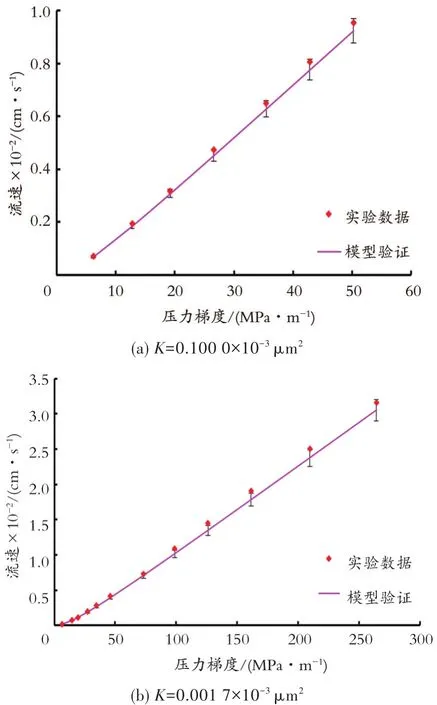
图6 计算曲线与实验数据对比Fig.6 The comparison of calculated curve with the experimental data

从图6中可以看出，新模型的计算曲线与样品6和样品7实验测得的渗流曲线比较吻合，误差约为5.00%，由此可见新的致密油藏非线性模型较为准确。

4 有效动用压力梯度

根据工业油流的最小日产量，换算为渗流速度，该最小渗流速度所对应的压力梯度即为有效动用压力梯度。

其中M=2.508K1.471+57.696K1.6268

根据式（9），可得真实有效压力梯度为：

则N为有效压力梯度与真实压力梯度的比值，可定义为“压力梯度有效利用率”。绘制渗透率不同的样品压力梯度有效利用率随压力梯度的变化关系，如图7所示。

由图7可知，随着压力梯度的增大，N呈对数形式逐渐增大。样品渗透率越大，N越大，表明流体流动过程中，压力损失越少。当压力梯度从0增大到20 MPa/m时，样品1至样品5的N分别为85.80%、70.65%、64.30%、26.11%、7.43%。主要因为渗透率越大，启动压力梯度越小，流体流动所需要克服的启动压力越小，用于流体产出的压力越大，因此N越大。同时可以看出，对于渗透率较低的样品在压力梯度较小时，压力损失极为严重，因此为了提高压力的有效利用率，在生产时应增大生产压力梯度，同时通过酸化、压裂等措施改善储层渗透率。

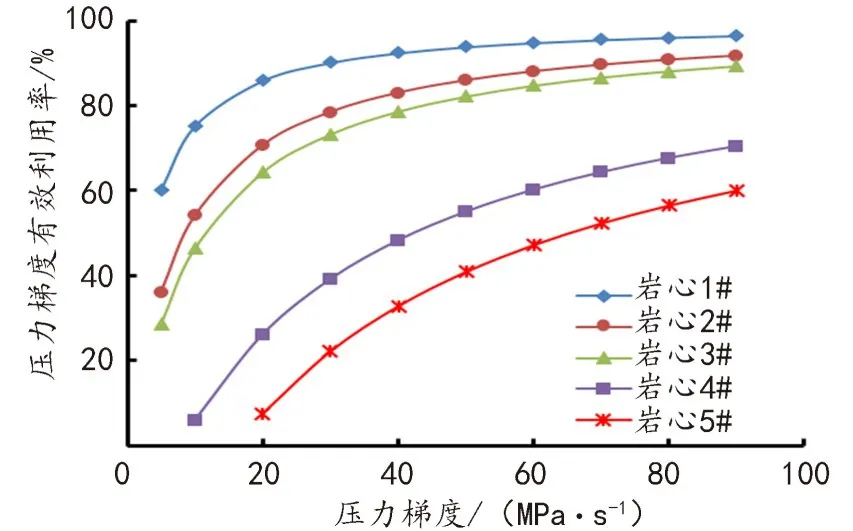
图7 岩心压力梯度有效利用率随压力梯度的变化Fig.7 Effective utilization rate of pressure gradient of core samples versus different pressure gradient

5 结 论

（1）考虑渗透率随储层压力的改变而不断变化的因素，对线性渗流模型进行修正，从而建立了适用于致密油藏的非线性渗流模型，通过验证模型发现，计算曲线与实验结果误差约为5.00%，表明新的渗流模型具有良好的准确性。

（2）根据建立的新模型画出了不同渗透率样品的有效压力利用率图版。随着压力梯度的增大，有效压力利用率呈对数形式逐渐增大；渗透率越大，有效压力利用率越大。因此在开采致密油藏时，应采取酸化、压裂等措施改善储层渗透率，同时在允许范围内应尽可能的增大生产压差，以提高压力梯度有效利用率。