一种航天用延时驱动装置的失效问题分析①

焦 静 ,李 端，梁 渭，张 波

(西安轻工业钟表研究所有限公司，西安 710000)

0 引言

目前，航天器一次性展开机构的动力源可以为弹簧的弹性力、弹性力矩或电机的驱动力矩，也有形状记忆合金的热驱动源等[1]。在现有的航天器中，大多采用电机和弹簧驱动，相较于电机驱动，纯机械式延时驱动装置有体积小、重量轻等性能优势，相较于弹簧驱动，延时驱动装置存在力矩大、力矩输出平稳等性能优势。机械式延时驱动装置越来越广泛的应用于航天领域。

某机械式延时驱动装置配套某型号伞状天线，作为天线关节处的驱动、锁定机构，完成一次性展开及锁定动作。本文结合驱动装置在天线地面调试过程中的一次故障，进行驱动装置的失效原因分析。

1 故障的发生

在XX卫星天线形面调试过程中，需要对天线进行多次收展，在产品上条操作过程中，7#肋展开机构和11#肋展开机构未听到控速轮系运转的声音。在随后的反射器展开过程中，目测7#肋和11#肋的展开速度比其它肋快，反射器展开到位功能正常。在反射器展开到位后，利用内窥镜对控时轮系进行检查，发现控时轮系的末级齿轴因轴肩断裂发生移位。内窥镜拍照如下图1，故障件的擒纵机构啮合状态，图2所示为正常机构的啮合状态。

图1 故障机现场观察状态Fig.1 Site status of the fault mechanism

图2 正常机构的啮合状态Fig.2 Meshing state of normal mechanism

失效断裂零件为平衡摆轴，平衡摆作为擒纵机构的组成，它的的失效将会导致产品延时功能丧失。初步可以判断，产品的上条异常现象、前次展开异常现象是控时轮系失效造成。

拆机检查情况如下图3：

图3 拆解过程照片记录Fig.3 Photo of dismantling process

2 延时驱动装置的原理及工作特性

在空间环境条件下，延时驱动装置应具有较大的驱动力矩、并能控速延时，展开角度75°，并且在展开到位后具有保持力矩及锁紧功能。

该延时驱动装置由铰链架即基体部件、驱动装置(控时轮系、增力轮系、动力源-发条)、上条机构、放条机构、展开部件及锁紧装置组成。其工作原理如下图4：

图4 工作原理框图Fig.4 Working principle block diagram

其中，擒纵机构包括平衡摆和骑马轮，是延时驱动装置中的重要组成部分。借鉴于钟表设计原理，本文的延时驱动装置中采用的是销式平衡摆，其作为无固有振动周期的振动系统，虽然周期的稳定性较低，但结构简单并且具有较高的可靠性，更适用于航天驱动器这种对结构可靠性要求高、延时时间精度要求相对较低的应用领域。

该延时驱动装置通过展开臂接口连接天线肋，在天线收拢后进行上条操作。装置在收拢过程中，增力及控速轮系各齿间为收拢方向工作面啮合，齿侧间隙位于机构展开过程时的工作面。机构工作时，锁紧机构释放，由于反向初始间隙存在，发条有一个空程回角。这时发条所释放的能量以冲击的形式施加给轮系。随着装置在展开方向的工作面全部啮合，冲击作用消失，机构正常工作至展开到位。

对于延时驱动装置的轮系来说，在初始工作时受到一个冲击载荷之后，在展开到位之前，承受一个恒定的工作载荷；综上，擒纵机构的平衡摆轴的正常工作过程中，先经历一个冲击载荷，再经历循环载荷。

3 断口分析

1)断口情况

图5是断轴的宏观断口图，图6为起始断裂区，图7是裂纹扩展区图，图8为瞬断区图[2]。

图5 宏观断口图 图6 起始断裂区图Fig.5 Macrograph of fracture Fig.6 Initial fracture zone

图7 裂纹扩展区图 图8 瞬断区图 Fig.7 Crack growth zone Fig.8 Final fracture zone

2)断口分析

断口经扫描电镜下观察，断口起始断裂区、扩展区均为脆性断裂，属于沿晶断裂，瞬断区域是典型塑性断口，断口处于零件几何尺寸变化较大的应力集中部位，对于周期性服役的零件易引起疲劳断裂[3]。

4 擒纵机构的疲劳强度分析

1)平衡摆轴受力分析

断轴为平衡摆轴，平衡摆与骑马轮组成无返回力矩的擒纵机构，该擒纵机构位于延时链路的最后级，具有延时的特性。

图9 平衡摆与骑马轮受力图Fig.9 Force diagram(1)

对骑马轮和平衡摆作用过程进行简化，得到平衡摆轴的受力图如下图10：

图10 平衡摆轴受力模型图Fig.10 Force diagram(2)

由图示中明确可以看出，断裂处受弯矩作用，并且为台阶轴应力集中部位，为整个零件强度最为薄弱环节。

2)应力集中系数

应力集中系数反映了应力集中的程度，是一个大于1的系数。应力集中是指物体中应力局部增高的现象，一般出现在物体形状急剧变化的地方。应力集中能使物体产生疲劳裂纹，也能使零件发生静载或冲击断裂。在应力集中处，应力的最大值(峰值应力)与物体的几何形状和加载方式等因素有关。而且试验表明，截面尺寸改变越剧烈，应力集中系数就越大。在阶梯轴截面的圆弧过渡的R值对阶梯轴截面的应力最大值影响较大，在设计时应对此处倒角进行严格控制。

某些典型的零件结构的有效应力集中系数如表图11～图13。

图11 阶梯轴在对称拉压的作用载荷形式下的有效 应力集中系数Fig.11 Effective stress concentration factor of stepped shaft under symmetrical tension and compression

图12 阶梯钢轴在弯曲载荷作用下的有效应力集中系数Fig.12 Effective stress concentration factor of stepped shaft under bending load

1—σb≥1000MPa1 2—σb=900MPa 3—σb=800MPa 4—σb=700MPa 5—σb=600MPa 6—σb≤500MPa图13 阶梯钢轴在扭转载荷作用下的有效应力集中系数Fig.13 Effective stress concentration factor of stepped shaft under torsion load

由应力集中系数图表曲线得，圆角的大小与应力集中系数呈类指数函数关系，即圆角越小对应力集中系数影响越大，尤其在R<0.04，圆角的进一步减小，应力集中系数增大加速。因而，圆角大小作为影响零件强度的十分敏感因素，尤其圆角下限要求，应予以严控，并且校核过程严格依照最小圆角条件进行。

在零件设计中，图纸标注习惯性将R角标注为R≤0.1，即未提出下限要求，在加工时按图纸执行导致应力集中现象的加剧。倒角的设计具有随机性，工艺控制难于实现，不是一个稳健设计。

应力集中的存在不仅有利于形成初始的疲劳裂纹，而且有利于裂纹扩展[5]，从而降低构件的疲劳极限。有效应力集中因数，是在材料、尺寸和加载条件相同光滑试样与有效应力集中试样的疲劳极限之比，即

σ-1光滑试样的对称循环弯曲疲劳极限，(σ-1)K有应力集中试样的对称循环弯曲疲劳极限，当R=0.1时，查图表，有效应力集中系数Kσ=1.55，(σ-1)K=411MPa对故障轴圆角检验，如下图14，上图为投影检测照片记录，下图为圆角投影样板，圆角由小到大依次为R0.02/R0.05/R0.08/R0.1。

图14 平衡摆轴倒圆角检测过程及样板Fig.14 Fillet detection process

经检验，平衡摆轴圆角值为R≤0.02，当R=0.02，依照图表取得

Kσ=3.2,(σ-1)K=199MPa

3)载荷作用下的强度计算

首先，进行稳定循环载荷阶段的强度分析：擒纵结构为高频运动部件，单次展开平衡摆作用4000多次，结合断口分析结果，主要进行轴的疲劳强度分析；同时由于断裂部位为轴肩处，为应力集中部位，因而必须考虑应力集中对疲劳强度的影响。

①疲劳强度参数的选取

末级擒纵机构，在正常工作中，平衡摆受到交变循环载荷，载荷作用结果主要考虑弯矩作用。金属的平均疲劳极限与屈服极限或强度极限之间的关系如表1所示。在本校核过程中，应力循状态为弯曲对称循环，因而取平均疲劳极限σ-1=0.49σb。对材料机械性能性能实测，材料抗拉强度达到1300MPa，因而其疲劳极限

σ-1=637MPa。

表1 金属的平均疲劳极限Tab.1 Average fatigue limit of metals

如上一节所述，结合应力集中系数计算零件在循环载荷工况下，经检验，平衡摆轴圆角值为R≤0.02，当R=0.02，依照图表取得：

Kσ=3.2,(σ-1)K=199MPa

②冲击载荷的产生原理

图15 齿轮侧隙示意图Fig.15 Gear backlash diagram

齿轮的侧隙是指装配好的齿轮副当一个齿轮固定时，另一个齿轮的圆周晃动量，以分度圆上的弧长计算。为了保证齿面形成正常的润滑油膜和防止由于齿轮工作温度升高引起的热膨胀变形致使齿轮卡住，齿轮在啮合时必须有适当的齿侧间隙。而有侧隙的的缺点是当齿轮副转向时会带来回程误差和冲击。这是轮系不可避免的结构特点。

针对本机构，在收拢后在展开时，由于间隙的存在，发条会有约5°～10°的空回角(根据试验过程观察)，5°～10°的空回角所释放的发条能量以冲击的形式施加在轮系上。每次展开过程，摆轴在正常工作载荷之外，还承受了初始冲击载荷。单次的冲击不足以使零件发生断裂，多次收拢展开，零件存在发生冲击疲劳断裂的危险。

③冲击载荷的计算

工程中常采用一种较为粗略但偏于安全的简化计算方法--能量法。用能量法进行分析时，为了计算简便同时又能满足要求，常进行以下假定：

1)不计冲击物的变形；

2)冲击物与构件接触后无弹回；

3)构件的质量(惯性)与冲击物相比很小，可忽略不计，冲击应力瞬时传遍整个机构；

4)材料服从胡克定律；

5)冲击过程中，声、热等能量损耗很小，略去不计。

在本次冲击问题中，由能量守恒原理，发条瞬间释放所产生的能量以冲击载荷的形式，加载给增力轮系。整个冲击过程，可以认为将发条释放的能量W转化为轴的变形能。即得：

W=ΣVεd

其中：W为发条产生的冲击载荷在整个冲击过程中产生的能量

ΣVεd为所转化成各级齿轴的变形能

发条释放的能量为冲击载荷作用在与条轴齿轮接触的轴上。在本结构中考虑简化模型，将能量全部作用在延时轮系，即传动轴。(简化的过程使零件强度计算趋于更加保守，因而计算为最小安全阈度)

发条储能：

其中：E为发条材料的弹性模量

h为发条厚度

b为发条宽度

n为发条释放圈数

L为发条长度

可直接计算出发条释放的能量。发条能量作用在被冲击构件上，由能量守恒定理，假设过程中没有能量损失，即W=Wεd，Vεd为被冲击的的构件(即传动轴3)的应变能。同时由机械能守恒定律来计算冲击载荷作用下被冲击物的最大动位移Δd及冲击应力σd。

若以静载的方式作用于构件上，假设静载为P，构件的经变形和静应力为Δst和σst，在动载作用下，相应的变形和应力为Δd和σd。在线弹性范围内，载荷、变形和应力成正比，故有：

定义动载荷系数Kd

同时有：

由上式可得：

结合上述分析，冲击疲劳强度计算结果如下：

表2 冲击疲劳安全系数Tab.2 Impact fatigue safety factor

冲击工况下，当R=0.02时，安全系数裕度小于1.5，不满足要求。

5 设计改进及验证

针对分析结果，由于冲击载荷的不可消除，因而主要考虑减小应力集中效应造成的零件疲劳强度的降低问题，针对应力集中进行结构改进[5]。

改进措施及影响如下图16：其中应力集中系数与R值及D/d相关。

图16 改进措施及影响分析Fig.16 Improvement measures and impact analysis

1)改进方案选择

2)改进具体措施

①改进台阶处圆角，圆角值由设计值R<0.1改为R0.1～R0.2，零件应力集中系数降低大于47%[6]；

②同时增大D与d，提高零件固有强度；

③在不改变接口，空间允许的条件线，改用轴承结构，将滑动摩擦变为滚动摩擦，减小了摩擦阻力，实现了在增大轴颈的基础上却不损失传动效率，同时轴承内孔的倒角可保证不干涉，大大提高了骑马轮轴、平衡摆轴的零件强度。

改进前后结构如下图17：

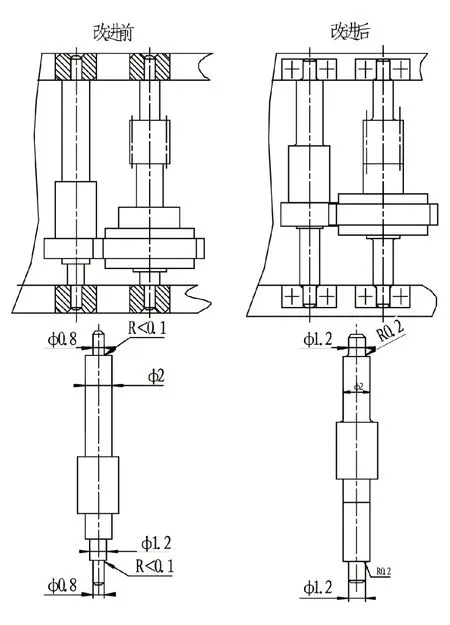
图17 装配示意图Fig.17 Assembly diagram

3)改进后设计校核

表3 改进前后平衡摆轴应力集中系数及安全系数Tab.3 Stress concentration factor and safety factor

4)措施有效性验证

平衡摆轴依照第2节进行改进设计，改进后的传动轴圆角的控制，投影检测为R2，如下图18，随后装配整机进行整机的试验验证。

图18 试验件平衡摆轴圆角控制情况Fig.18 The stiuation of fillet control

整机试验目底：考核改进后延时驱动装置的可靠工作次数。

试验产品状态：平衡摆轴改进后的整机。

试验项目及试验件数量见表4：

表4 测试项目及数量Tab.4 Test items and quantity

平衡摆轴改进后，延时驱动装置依次进行上述试验，试验均得到通过，寿命试验完成600次无故障展开试验，延时驱动装置的功能、性能正常。经验证延时驱动装置的失效分析准确，改进措施可行有效，经改进设计大大提高了其无故障工作次数。

6 结论

针对延时驱动装置发生的失效问题，进行了以下失效分析。

结合产品的使用工况，进一步识别产品的工作特性，识别出冲击载荷，分析冲击产生的机理并进行计算；进行了擒纵机构的受力分析，同时考虑了应力集中的影响，最终对延时驱动装置(主要对失效轮轴)工作时的结构强度进行较为准确的计算。根据分析结果形成改进措施，并对改进后的延时驱动装置整机进行了试验验证。