湍流模型在对转桨梢涡模拟中的适用性分析
2020-03-04王英铸毛翼轩苏金波王晴胡健
王英铸,毛翼轩,苏金波,王晴,胡健
(1.哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001;2.中船黄埔文冲船舶有限公司,广东 广州 510715;3.中国舰船研究中心 船舶振动噪声重点实验室,湖北 武汉 430064)
随着全球航运业的发展,人们对海洋航行推进设备的推进效率、空化、振动和噪声不断地提出更高的要求。相比于传统单螺旋桨对转桨在推进效率上提高明显。Kraritz[1]针对DDG-51驱逐舰设计的单桨和对转桨进行研究分析。结果表明,相比于传统螺旋桨,对转桨在设计工况下的推进器效率提高了9%左右,在某些非设计工况下,推进效率提高幅度可达20%,配备对转桨后,DDG-51每年燃油节省总量为8.8%。
对转桨在水下推进中的优势突出,受到研究人员的密切关注。对转桨系统采用模型试验方法研究是很困难的,主要原因在于对转系统机构复杂,使得试验装置相比于单桨要复杂的多,带来试验成本的上升和数据采集和测试难度增加。随着流体力学理论研究的深入,逐渐发展出了4个主要的湍流计算模型:直接数值模拟(direct numerical simulation,DNS)、雷诺平均数值模拟(Reynold averaged navier-stokes,RAV)、大涡模拟(large eddy simulation,LES)和分离涡模拟(detached eddy simulation,DES)。数值模拟已经可以完成大部分对转桨模型试验的工作,能够提供远比模型试验丰富的整个流场的可靠信息。任海奎等[2]对混合CRP推进器前桨的敞水水动力性能进行了数值计算与试验验证,吊舱后桨提高了前桨的推进效率,并有效地消除了前桨桨后穀涡。王展智等[3]采用不同的雷诺平均纳斯-斯托克斯方法模型计算了对转桨的水动力参数,并讨论了时间步长的计算收敛性分析,为对转桨水动力性能数值计算提供了参考。Paik等[4]通过Fluent流体计算软件,采用RANS法和滑移网格技术对船后对转桨尾流场进行数值模拟,并利用三维粒子图像测速技术测量技术完成了模型试验的流场测量,经过对比,数值结果能够与同尺度模型试验结果较好地吻合,并且数值结果同文献[5-8]采用类似方法得到的结果相吻合。对转桨除了能减少能耗外,还具有降低振动噪音、改善空泡性能的优点[9]。对转桨推进性能的研究方法已趋于成熟,但对于对转桨工作中的振动、噪声、空化以及前后桨的干扰问题的研究尚未完备。而螺旋桨的梢涡经常和梢涡空化联系在一起。梢涡空化是螺旋桨最先出现的空化现象。对转桨梢涡是影响对转桨推进效率、空化性能、振动和噪声的重要因素之一,梢涡脱落后向后传播还会引起船尾舵设备空化剥蚀以及振动等问题。
Ghias等[10]在分析了Martin等[11]对NACA2415翼型的实验后,采用大涡模拟技术对空气中NACA2415翼型的翼尖可压流进行了数值模拟,重点对尾流中的梢涡进行了模拟。Guilmineau等[12]分别采用2种RANS方法,基于 SST模型的RANS法和基于各向异性双方程显示迭代雷诺压力模型(explicit algebraic reynolds stress model)的RANS法以及基于 模型的DES方法,对INSEAN E779A型螺旋桨周围流场分布和梢涡进行了数值模拟,进过对比,其数值结果与实验测量结果贴合度很高。耿冲[13]采用大LES方法对对转桨梢涡进行了初步的研究。Yamanishi等[14]利用大涡模拟技术对涡轮泵的尾涡进行了数值模拟,模拟结果较为符合实验测量,并且给出了实验难以给出的新发现,具有较高的参考价值。
本文采用软件STAR-CCM+完成计算网格的划分以及CRP6型对转螺旋桨梢涡数值模拟。完成RANS模型、DES模型和LES模型的宏观水动力计算验证。通过梢涡模拟结果的对比分析,讨论上述3种模型对对转桨梢涡的模拟精确度,并对对转桨梢涡以及尾流场的物理特性进行研究。
1 数学模型和网格划分
1.1 三维模型
CRP6型对转桨的几何模型如图1所示,计算的初始位置前后桨桨叶夹角为45°。前后2个桨的几何参数如表1所示[15]。
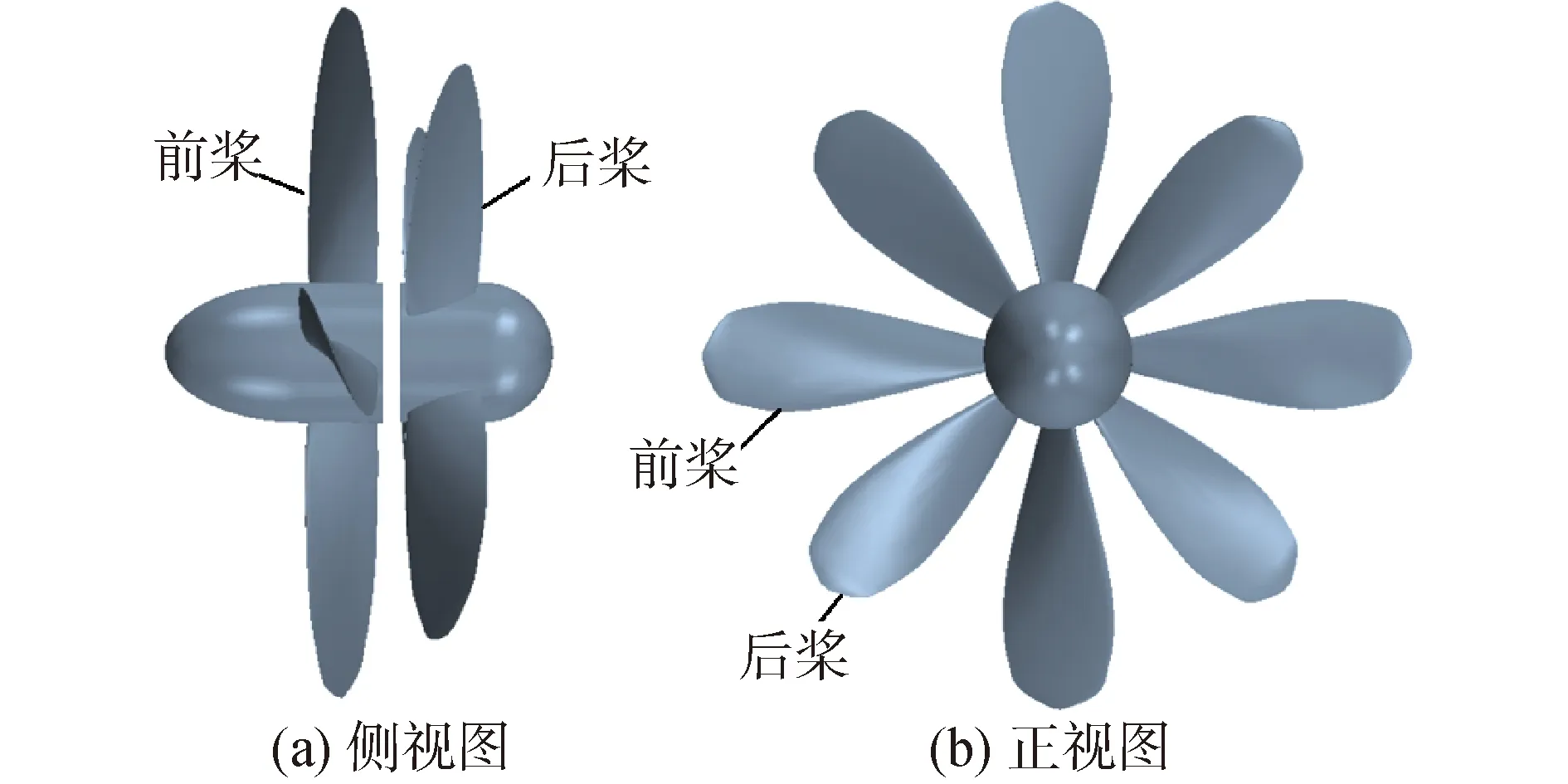
图1 CRP6三维模型Fig.1 3D model of CRP6

表1 CRP6型对转桨主要参数Table 1 Specification of CRP6
1.2 数值计算方法
本文在求解对转桨的流场时采用的是粘性流体力学方程。具体控制方程为:
1)连续方程:对于控制体V而言,控制体的质量不随时间变化,由密度ρ增加导致的增质量加和沿表面积S流出控制体的减少质量其和为0,即:
(1)
式中V为体积。
对于不可压流体,式(1)也可以简化为:

(2)
2)运动方程:粘性流体的运动方程也称为N-S方程,其积分形式为:
(3)
式中:f为单位质量的体积力;p为单位面积的表面力;A为面积。
对于牛顿流体,且运动粘性系数μ恒定时,微分形式为:
(4)
式中v为流体速度。
(5)
能量方程式能量守恒定律在流体流动中的表达形式。在控制体中能量的变化率等于单位时间内,质量力f和表面力p所做的功及与外界交换的热量,积分形式为:
(6)
式中:e为分子热运动的动能;T为温度;K为传热系数;Pn为法向压力。
微分形式为:
(7)
式中cp为等压比热。
1.3 计算域及网格划分
计算域设置如图2所示。CRP6前桨半径用R表示。计算域沿桨轴方向长度为10.0R,计算域宽和高均为10.5R;对转桨中心距计算域入口距离为3R,距离计算域出口为7R,计算域周向4个平面均为对称平面;由于前后桨旋向相反,分别为前后桨设置1个旋转域;旋转域旋转运动以及旋转域和静止计算域之间的数据传递通过重叠网格实现。计算域入口流速设置为3.3 m/s,对转桨前后桨转速均为12 r/s,即进速系数J为0.9。

图2 计算域划分和边界设置Fig.2 Definition of computational domain and boundary condition
湍流模型对对转桨梢涡数值模拟的适用性分析中首先要保证网格精度和时间精度的一致。网格划分中,网格加密区域包括对转桨旋转域和桨后6.0R的距离范围,加密区网格尺寸为0.026 2R,加密区网格划分结果如图3(a)所示。壁面网格划分时,边界层网格满足y+值小于等于1,如图3(b)所示。桨叶表面网格尺寸为0.008 2R。棱柱层层数为3层,增长率为1.5,静止域为0.902×106,计算域网格总量约为7.95×106。表2给出了网格分布细节。

表2 网格分布细节Table 2 Details of grid cells distribution

图3 流场对称面和近壁面网格划分结果Fig.3 Views of grid in symmetry plane and near the rigid wall
流场非定常计算中,时间步长对计算结果影响很大。文献[16]中提出,在湍流中,每一流体微团的速度、压力、温度等物理量都在迅速的变化其频率范围为1~106Hz。因此,对螺旋桨梢涡的模拟需要采取非常小的时间步长。本文时间步长为2.893 5×10-5s,库朗数为0.024。对转桨前后桨转速为12 r/s,即每个时间步长前后桨各自转动0.125°。
2 对转桨敞水特性及梢涡模拟
2.1 对转桨敞水水动力性能
本节分别采用不同湍流模型(RANSk-ε、DES和LES)对CRP6型对转桨敞水水动力性能进行计算,并与实验数据进行对比。计算工况为:进速为3.3 m/s,对转桨前后桨转速为12 r/s,即进速系数J为0.9。计算结果如表3所示。其中,KTF、KQF和KTA、KQA分别表示前桨的推力系数、转矩系数和后桨推力系数、转矩系数;KT、KQ和η分别表示对转桨总推力系数、转矩系数和总效率。从表3结果可以看出,3种物理模型对前后桨推力系数的模拟结果与实验值都比较接近,推力系数误差均小于3.5%,其中前后桨各自力矩系数的计算结果误差比较大。综合来看,在1.3节中给出的网格分辨率和时间分辨率下,采用RANS模型得到的水动力计算精度更高。
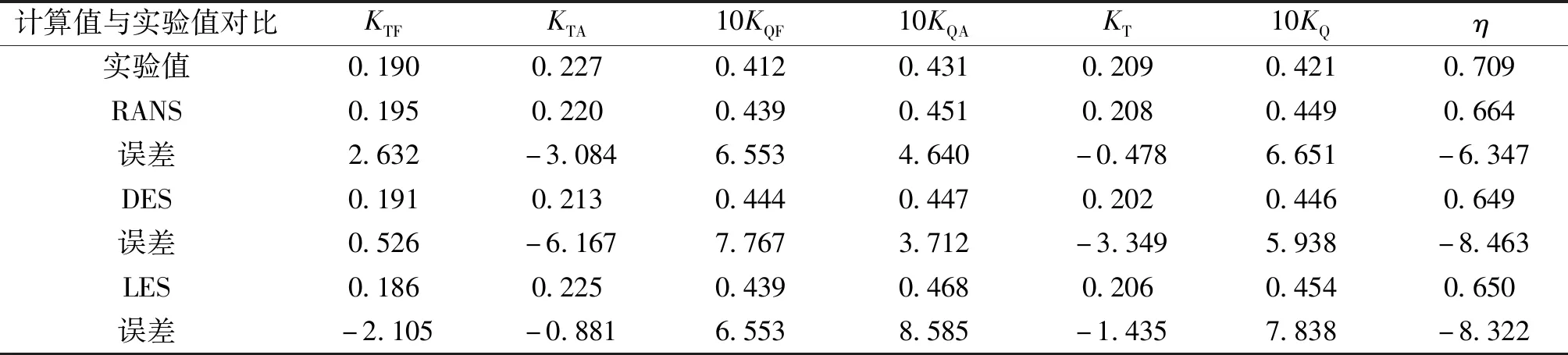
表3 RANS、DES和LES模型数值模拟结果Table 3 Numerical results obtained with RANS,DES and LES
2.2 对转桨梢涡数值模拟
本节讨论选择不同湍流模型(RANS、DES和LES)对对转桨梢涡的模拟的影响。数值计算的网格精度和时间精度保持一致。采用Q判据函数可视化处理对转桨梢涡,函数值取Q为1 000/s2。
数值模拟的后处理结果中,为了便于分辨前桨梢涡和后桨梢涡,梢涡可视化处理采用的标量函数设置为沿桨轴方向的涡量值。在流场设置水平截面和垂直于桨轴的截面监测计算域的速度场。
DES模型对单螺旋桨的梢涡模拟结果中梢涡的形状等和空泡水筒的实验非常接近,而RANS模型计算得到的单桨梢涡,在离开螺旋桨后很快消失。DES模型对单桨梢涡的模拟精度要高于RANS模型。但是,如图4(a)、5(a)所示,对转桨的梢涡模拟中,通过3种物理模型的模拟结果显示,同等网格和时间精度下,DES模型与RANS模型的计算结果中梢涡的产生、演化、前后桨梢涡的相互干扰以及离开对转桨一定距离后涡的耗散等均非常近似。对转桨梢涡随尾流向后运动至很远的距离。对转桨梢涡中前桨梢涡涡管较细,梢涡在交叉位置很快断开。由于前后桨梢涡之间的相互诱导,对转桨后方3.0R后的对转桨梢涡结构复杂,并且耗散严重。
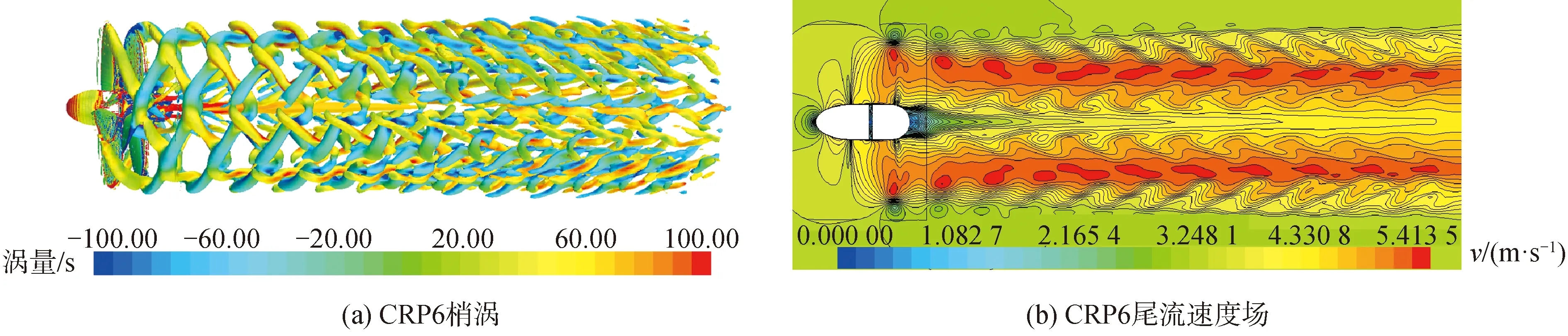
图4 RANS计算结果Fig.4 Numerical results obtained with RANS
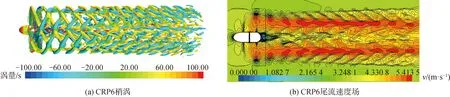
图5 DES计算结果Fig.5 Numerical results obtained with DES
两者之间最明显的不同在于RANS模型计算结果中毂涡较少,并且大部分毂涡在尾流中快速消散。如图4(b)、5(b)所示,对比DES模型和RANS模型计算得到的流场速度分布结果,DES模型对桨后速度场的非定常流动捕获更加充分,尤其是在桨毂后方的区域。
通过对转桨梢涡计算结果的对比,所采用的3种湍流模型计算得到的对转桨梢涡结构、位置和演化规律都非常接近。在同等时间和网格精度下,LES模型对流场涡结构的计算更加精确。从图6可看出,LES模型的计算结果中,前桨梢涡和后桨梢涡均可以清晰分辨。从流场速度场分布也可以清晰看到前后桨梢涡的位置、桨后毂涡流场以及非稳态流动特征。前后桨梢涡均呈近似螺旋线状向对转桨后方运动。前桨梢涡在通过后桨盘面时受到后桨叶梢的周期性诱导,涡管形状改变。前后桨梢涡随对转桨尾流向后运动的过程中,梢涡与梢涡之间的相互干扰也会使梢涡涡管形状逐渐改变。

图6 LES计算结果Fig.6 Numerical results obtained with LES
以对转桨后桨盘面中心为原点,沿对桨轴方向向后x=0.56R和x=4.0R处设置横向截面,监测对转桨后方不同位置的流体速度场分布,如图7~9所示。DES模型的求解过程中,对平衡湍流或类似平衡湍流中采用RANS求解,而对非平衡复杂湍流采用LES求解。CRP6后桨桨叶近后方位置为类似平衡湍流区域,因此,图7(a)和8(a)中除了桨毂正后方小范围流域外,其他位置的速度场分布基本相同。Guilmineau[12]的研究结果也印证这一点。而对转桨后方较远位置(x=4.0R)的速度场分布相差较大。
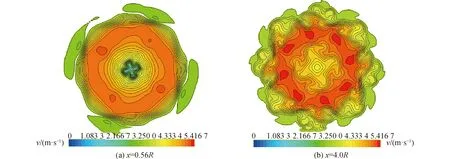
图7 RANS模型计算得到的速度场横向分布Fig.7 Lateral velocity distribution RANS

图8 DES模型计算得到的速度场横向分布Fig.8 Lateral velocity distribution DES
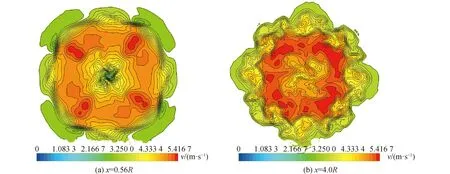
图9 LES模型计算得到的速度场横向分布Fig.9 Lateral velocity distribution LES
图9中LES模型的求解得到的速度场横向分布与图7和图8相差明显。图9(a)中,前后桨梢涡位置的速度梯度和桨毂后方流场湍流度均较大。从图9(b)中可以看出,对转桨梢涡随尾流向后运动过程中,由于梢涡之间的相互干扰,梢涡流场结构越来越复杂。图10为前后桨的周向诱导速度。

图10 LES模型计算得到的周向诱导速度Fig.10 Tangential velocity distribution LES
将加密区网格尺寸由0.026 2R减小至0.019 7R,总网格量增加值1.474×107。为了减少计算量,将时间步长设置为5.787×10-5s。采用LES湍流模型对对转桨梢涡进行数值模拟。对转桨梢涡的可视化处理结果如图11和图12所示,Q=1 000/s2。
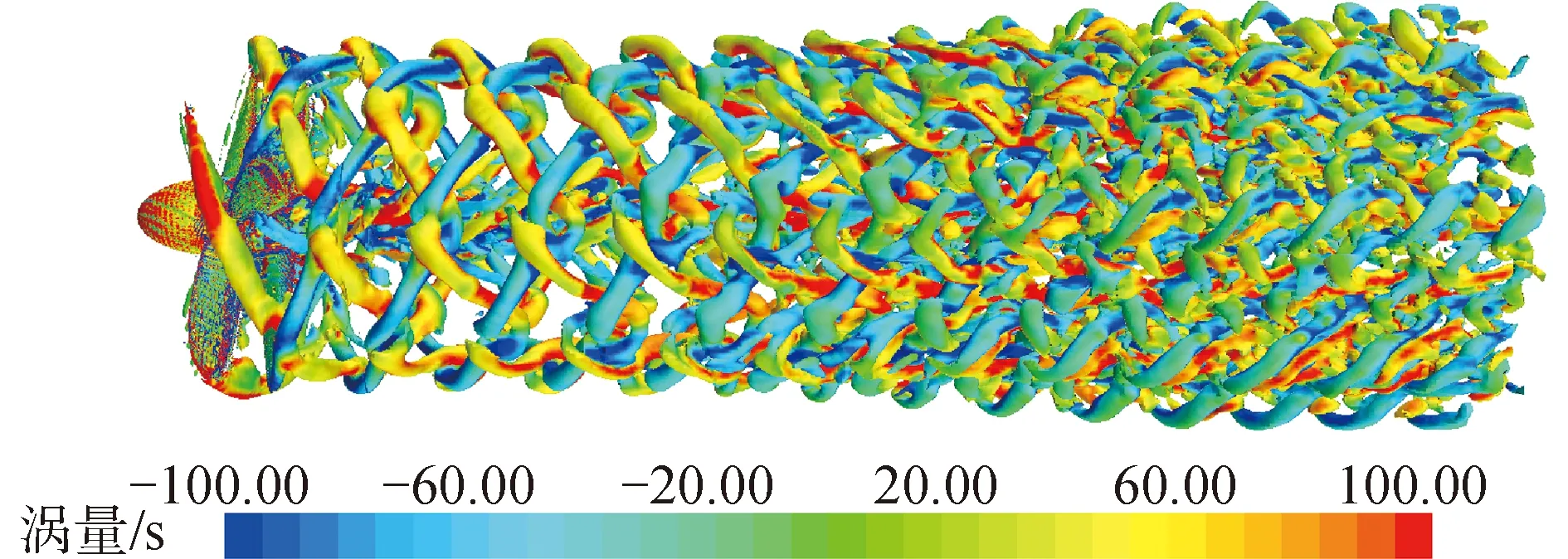
图11 改变网格和时间步计算得到的对转桨梢涡(LES)Fig.11 Tip vortex of CRP6 calculated with new grids and time step (LES)
从图11中可以较为清晰的看出CRP6前后桨梢涡交叉位置的缠绕规律。后桨梢涡在前桨梢涡的诱导下逐渐弯曲,而前桨梢涡逐渐以后桨梢涡为中心环绕。对转桨距后桨盘面3.0R后的梢涡结构复杂,但部分梢涡缠绕规律从另一个角度仍可以清晰分辨,如图12所示。

图12 对转桨梢涡侧后视图(LES)Fig.12 Rear side elevation of tip vortex(LES)
3 结论
1)对比对转桨敞水水动力性能数值预报结果和实验结果,上述3种湍流模型的数值预报结果与试验值均吻合良好,其中RANS模型的计算误差最小。RANS模型在对转桨水动力载荷的计算中具有良好的效果。
2)对于非平衡的复杂湍流如对转桨梢涡、毂涡等问题,LES模型的模拟结果更好。采用LES模型计算对转桨梢涡时,对转桨梢涡结构以及演化规律可以清晰分辨,LES模型在精确捕捉梢涡和清晰展示湍流特征方面很有优势。
本文重点关注对转桨的梢涡数值模拟,通过3种模拟方法的对比,得出LES模型对梢涡模拟效果最好的结论,目前对对转桨梢涡的研究不多,本文的工作可为梢涡模拟提供参考。
