城市高中压配电网协调性综合评价研究*

刘 超 张 鹏 张寓涵 赵 刚 吴延琳 岳园园

（国网陕西省电力公司经济技术研究院 西安 710075）

1 引言

高压配电网作为输电主网的末端，承担者向中压配电网提供优质电能的任务；中压配电网是连接高压配电网与用电客户之间的桥梁。高中压配电网的协调性指的是高压与中压两个电压等级、不同设备之间的相互匹配与兼容程度。当高中压配电网中任一环节出现欠协调的问题时，都将会导致配电网出现供电可靠性降低，供电质量下降，供电经济性差，甚至无法满足用电客户的需求［1］。高中压配电网只有实现较好的协调，才能避免配电系统内部出现供电瓶颈，保持电网运行的可靠性、安全性及经济性，提高配电网的效益。

城市配电网的协调发展，既包括高压配电网内部的协调性，又包括中压配电网内部的协调性。目前，国内外的文献对电网协调性的研究主要集中于高压或者中压配电网的规划、结构、容量评估以及电网与电源、电网与负荷、电网与社会环境［2］等方面，而缺乏对高压和中压配电网两个电压等级的协调程度进行研究。

文章充分考虑影响高中压配电网协调性的多种因素，在传统的只考虑高压或者中压配电网协调程度的基础上，又考虑了高中压变压器容量配比、高中压线路容量配比以及变电站出线均衡度等三个指标，全面衡量高中压配电网的配合协调程度。

2 城市高中压配电网协调性指标体系

高压配电网的协调性，指的是高压配电网内部变电站、线路的容量、结构以及负载情况配合的协调程度；中压配电网的协调性，指的是中压配电网内部配电变压器以及配电线路的结构、负载、容量以及间隔利用等指标的合理程度；高中压配电网的协调性，指的是高压配电网与低压配电网之间在变压器容量、线路容量以及负载与间隔的利用情况等配置的合理性。

本文基于层次分析法，从高压配电网协调性、中压配电网协调性以及高中压配电网协调性［6］三个方面构建指标体系，如图1所示。

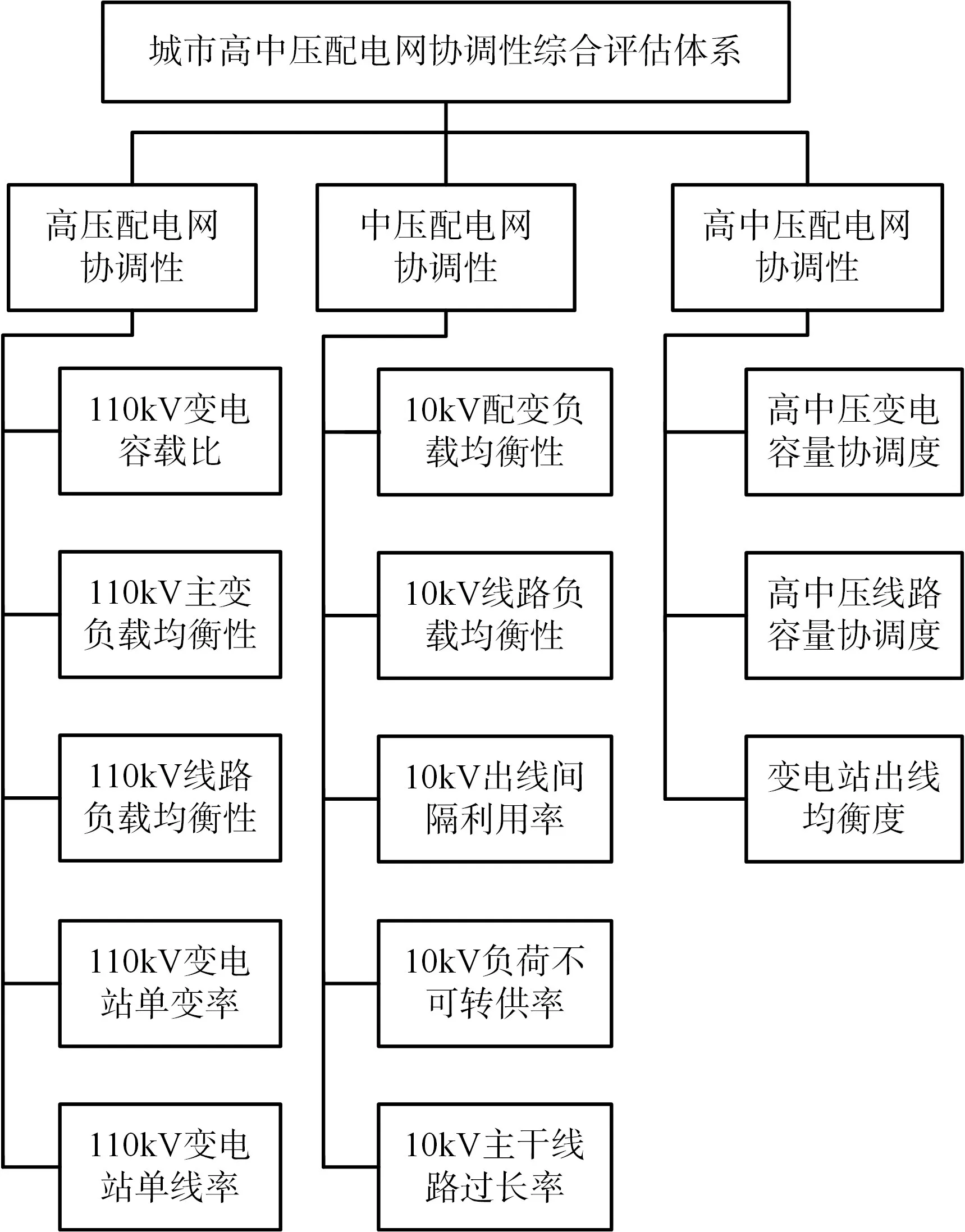
图1 城市高中压配电网协调性指标体系

对图1中的评价指标进行分析，其中，指标定义明确、计算较为简单的指标计算方法如表1所示，其他指标需要进行指标定义、含义分析以及计算方法需具体介绍。

1）负载均衡性指标［8］

负载均衡性指的是设备负载率相对于均值负载率的均衡程度，可分为变压器负载均衡性和线路负载均衡性。

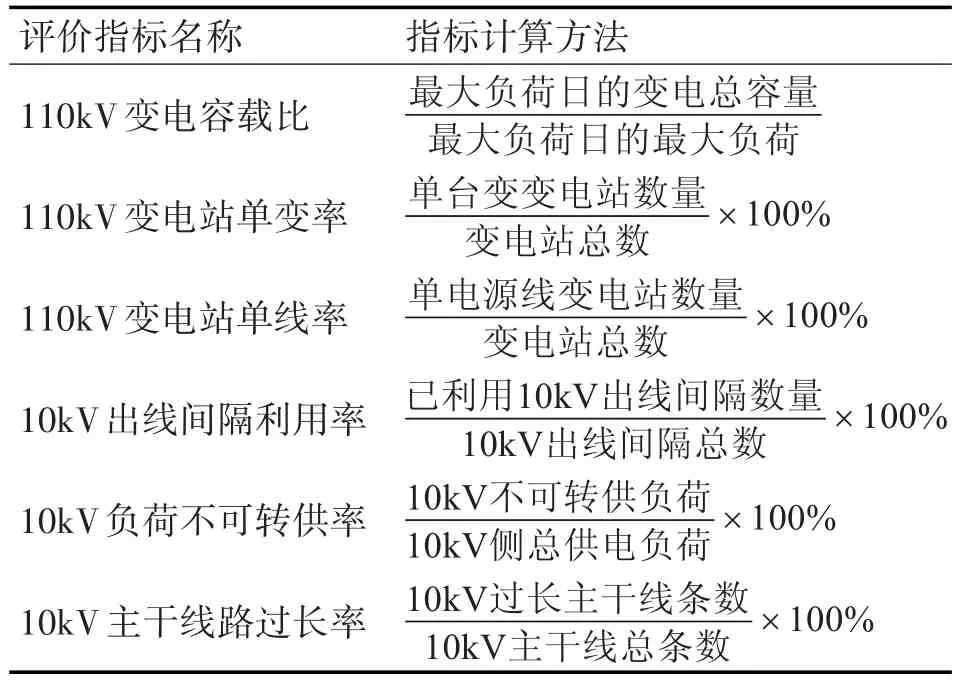
表1 部分评价指标的计算方法

设某评估区域内有待评价设备（变压器或者线路）的数量为N，某个设备i的负载率μi的表达式为

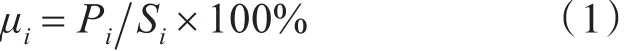
式中，Pi为设备i的负载值，Si为设备i的额定容量。所有设备负载率的均值μavg的表达式

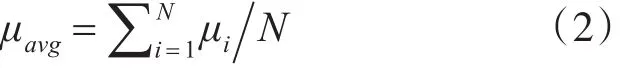
选择设备负载率标准差δ（其中，变压器负载率标准差为δT，线路负载率标准差为δL）表征各设备负载率的均衡程度。δ值越大，表明设备负载率偏差越大，设备的负载越不均衡。

将该指标转换为设备负载均衡性指标A（其中，AT为变压器负载均衡性指标，AL为线路负载均衡性指标）。

A为正向指标，即A越大，设备负载均衡性越好。

本文中，AT1为110kV主变负载均衡性指标，AT2为10kV配变负载均衡性指标AL1为110kV线路负载均衡性指标，AL2为10kV线路负载均衡性指标。

2）高中压设备容量协调度［2］

对于城市配电网而言，高压配电网的设备容量SH即为110kV设备额定容量之和，中压配电网的设备容量SM即为10kV设备额定容量之和。定义高中压设备容量配比ε（其中，εT为高中压变电容量配比，εL为高中压线路容量配比）：

理论上而言，高压设备容量与中压设备容量的比值为1时，二者之间的协调性最好［7］。但考虑负荷同时率等因素的影响，一般取高压与中压配电网设备容量的最佳比值ε0为（εT0为高中压变电最佳容量配比，εL0为高中压线路最佳容量配比）0.9。ε越接近ε0，则高中压配电网设备容量协调程度越高。将ε转换为正向指标，定义高中压变电容量协调度指标α：

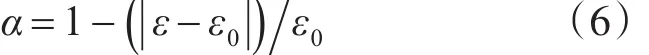
α值越大，则高中压配电网设备容量协调度越高。

3）变电站出线均衡度

变电站出线均衡度指的是110kV变电站的10kV出线均衡度，定义为变电站10kV间隔利用率与变压器负载率的比值，该指标的意义在于衡量110kV变电站10kV出线规模的合理程度［9］。该指标为中间值指标，根据文献［4］，该指标的合理取值为1.2～1.7。变电站出线均衡度越大，表明变电站的10kV间隔利用程度越不充分；变电站出线均衡度越小，表示变电站的10kV间隔的平均负载率越重。

3 城市高中压配电网协调性指标权重与评分标准

3.1 评价指标权重的确定

指标权重的确定方法包括主观赋权法和客观赋权法。主观赋权法需借助专家经验进行权重确定，过程简单，用于指标数较少的情况；客观赋权法以数学理论为依据，借助数学模型，得到的权重结果客观量化，消除了人为因素的影响，可用于多指标的权重确定。本文依据主观赋权法与客观赋权法的优点与不足，采用基于德尔菲法修正的层次分析法（AHP-Delphi）进行指标权重的确定［5］。该方法的具体步骤如下：

1）对待评估指标体系建立层次结构。对于本文中研究的问题，建立了目标层、准则层及指标层的三层结构。

2）构建评价指标的判断矩阵。依据AHP理论，对同一层次的m个指标，依据萨蒂的1～9重要性标度方法，建立两两比较的判断矩阵

式中，aij为同层次指标i和j之间相对于上层指标的重要性表征，且aji=1/aij。

3）对判断矩阵进行指标赋值。引入德尔菲法进行各判断指标的赋值，由n位行业专家对判断矩阵A进行独立赋值，形成n个不同的判断矩阵。

4）对判断矩阵进行优化处理。由于专家分析问题的角度不同以及专家经验的差异，可能使判断矩阵结果差异较大，数据分析不合理，因此需要对判断矩阵进行优化处理。具体方法如下：

（1）对n个判断矩阵的每一组指标求取平均值，形成平均值矩阵Aˉ：

（2）设置判断阈值的范围为［0.5aˉij，1.5aˉij］，对每位专家初始判断矩阵中的相对权重值与平均值矩阵中的数值进行比较，若第k个判断矩阵中存在数值超过预设阈值的情况，则认为该矩阵数据无效，将该矩阵剔除。最后，得到n'个有效的判断矩阵。

（3）平均化处理n'个有效的判断矩阵，得到经过优化处理的判断矩阵

5）计算优化判断矩阵的指标权重。

6）评价指标一致性检验。若一致性检验通过，则得到了评价指标的权重；若一致性检验未通过，则重新收集专家的意见，回到步骤2）进行计算，直至一致性检验通过为止。

3.2 评价指标的评分

使用德尔菲法对评价指标进行评分，邀请电力系统专家确定指标的评价标准。本文所述的评价指标包含数值越大越好的正向指标、数值越小越好的负向指标和数值在某一区间内为最优的中间值指标［10］。正向指标和负向指标均按照标准分数的间隔进行打分，中间值指标分为低值分数和高值分数，表示中间值指标在某一范围内最优。评分分数以百分数表示，高压配电网协调性指标的指标值与评价分数的对应关系［3～4］如表2所示。

表2 高压配电网协调性的指标值与评价分数的对应关系

由于评价分数是离散的，为使评分分数更易计算，对该离散的评分分数使用Curve Expert工具进行曲线拟合，得到评分函数如表3所示。

在得到指标层各项评价指标的得分以后，按照递推原则，将各指标的相对权重与评分进行相乘加权求和，依次得到准则层及目标层的最终评分。

表3 高压配电网协调性的指标评分函数

4 算例

本文选取某城市开发区配电网为例，进行高中压配电网协调性分析。该区共有110kV变电站4座，主变8台，变电总容量为400MVA，110kV线路为单辐射接线，110kV变电容载比为2.26，无单线或单变的变电站，有一座变电站主变负载率超过80%，一座变电站为新投运站，负载率在20%以下，其他两座变电负载率在50%左右；110kV变电站的10kV出线间隔共38个，已利用29个，其中专线间隔9个，公用线路间隔20个。该地区为新开发区域，无35kV电压等级，10kV公用配变共2632台，配变容量共452.5MVA，无高损配变；10kV线路均为电缆线路，供电半径平均为4.2km，有5条线路供电半径较长；10kV线路均为双射接线形式，线路间基本实现互联，但故障情况下负荷无法完全转供。

依据前述的指标权重及评价分数的确定方法，得到该地区高中压配电网协调性指标的相对权重及评分，如表4所示。

由表4可计算得到该地区城市高中压配电网协调性的综合评价得分是82.0分。其中，高压配电网协调性得分较高，但110kV主变负载率分布不均衡，存在部分重载或轻载现象中压配电网协调性指标中，10kV配变负载均衡性得分不高，10kV部分负荷无法转供；高中压配电网协调性指标中，高中压线路容量协调度指标需要进一步提升。在今后的规划工作中，该地区应考虑进行负荷切改，着力解决地区110kV主变、10kV配变负载分布不均问题，提高负荷可转供率，更换部分老旧电缆线路，减少重载线路，提高高中压线路的容量协调程度，进一步保证地区负荷发展。

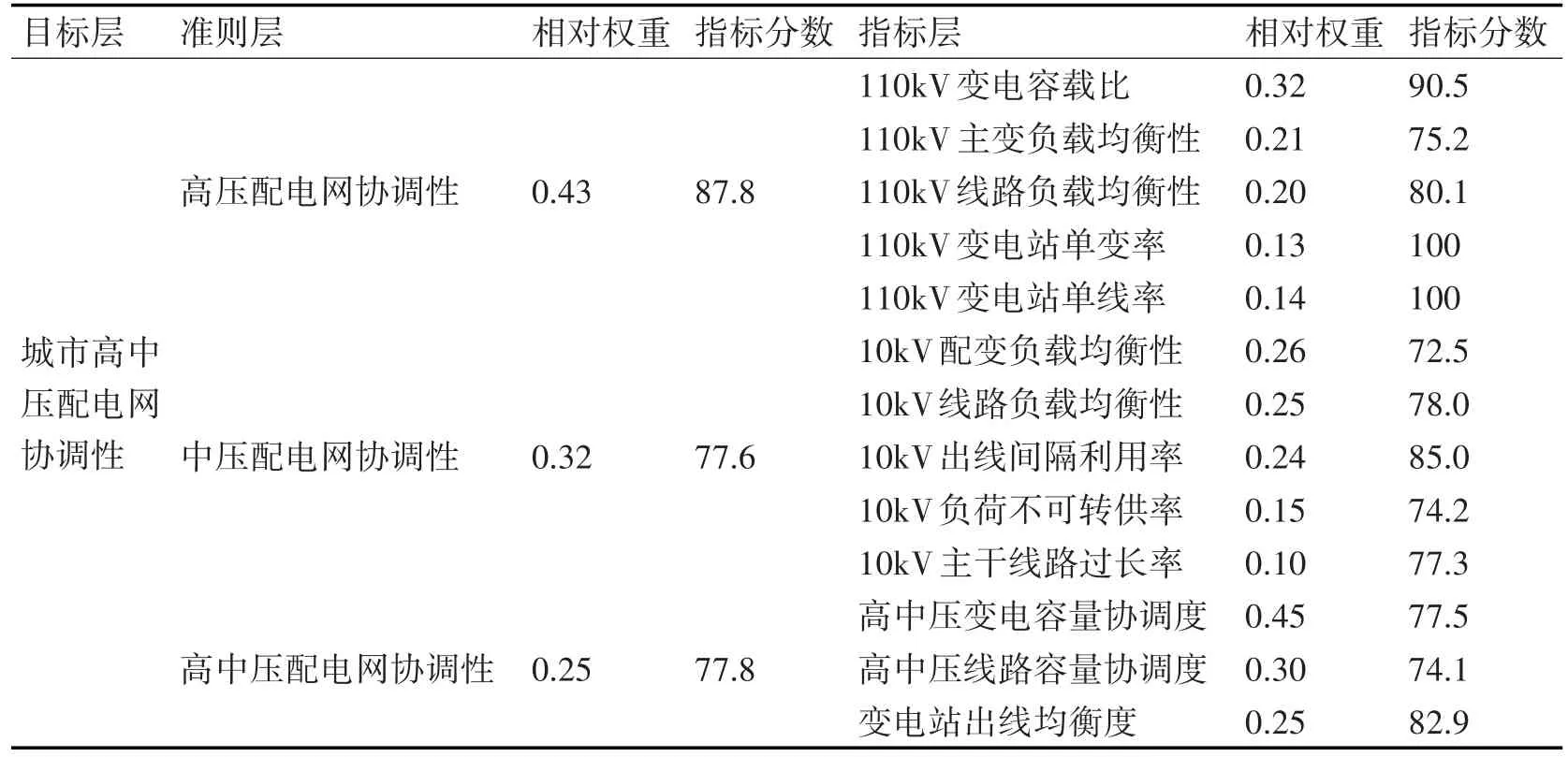
表4 指标的相对权重及评分

5 结语

高中压配电网的协调发展是供电可靠性、安全性的重要保证。本文建立了城市高中压配电网协调性分析的指标体系，使用基于德尔菲修正的层次分析法确定了指标权重，使用德尔菲法进行指标评分，并将离散的评分进行曲线拟合，建立了城市高中压配电网协调性综合评价模型。

最后，通过对某地区高中压配电网进行协调性分析，发现了该地区配电网在高压与中压配电网协调发展方面存在的问题，指导该地区配电网的发展建设。实例证明，该评价模型在进行配电网发展协调性方面具有较好的效果，可指导地区配电网的规划发展。