大学基础课课程成绩加权投票预测模型研究

陈佳明 骆力明 宋洁

摘  要： 针对教育领域特定应用场景，利用数据挖掘技术处理教育数据是目前热点研究问题之一。课程成绩预测指对一门课程学生的期末成绩进行预测，其关键问题是通过选取合适的学生特征和确定最优的预测算法来构建预测准确率高的模型。针对大学基础课的特点，从主客观两方面选择特征，对比了4个效果最优的课程成绩预测分类算法，以准确率较高的算法构成加权投票集成算法，发现加权投票集成算法的预测准确率和AP值最高，为利用数据挖掘技术实现课程成绩预测提供了一种有效的方法。

关键词： 成绩预测模型; 教育数据挖掘; 加权投票集成算法; 模型构建; 大学基础课; 分类算法

中图分类号： TN911.1?34; TP391                   文献标识码： A                    文章编号： 1004?373X（2020）01?0093?06

Course performance weighted voting prediction model of college fundamental courses

CHEN Jiaming， LUO Liming， SONG Jie

Abstract： To process the educational data from specific application scenario in education field by data mining technology is one of the popular research projects. Course performance prediction refers to the prediction of final performance of students in a curriculum， whose key issue is to build a high?accuracy model by selecting proper student features and determining optimal prediction algorithm. The features are selected from both subjective and objective aspects according to features of university basic courses. Four optimal classification algorithms of curriculum performance prediction are compared and the weighted voting integrated algorithm is constituted with the algorithms with higher accuracy. The weighted voting integrated algorithm can reach the best accuracy and AP value， which provides an effective method for realization of curriculum performance prediction by utilizing data mining technology.

Keywords： performance prediction model; educational data mining; weighted voting integrated algorithm; model construction; college elementary course; classification algorithm

0  引  言

教育數据挖掘（Educational Data Mining，EDM）是近年来热门的数据挖掘研究领域之一，可以为教师提供用于评估的信息，为教师设计与调整教学环境和方法的决策提供教学基础[1]。学生成绩预测是教育数据挖掘领域的重点研究课题之一[2]。学生成绩的预测分为总体学业预测和课程成绩预测两类。其中，总体学业预测是对一个持续时间较长的教学过程（如某一学年或本科四年）中大学生整体的学习情况进行观察，预测大学生学年末或毕业时的学业表现。例如，文献[3]以巴基斯坦某信息技术专业学生大学四年的课程成绩作为输入，预测学生毕业设计的成绩。课程成绩预测比总体学业预测更有针对性，是指对一门课程（在线课程或者课堂教学）学生的期末成绩进行预测。预测结果可以辅助教师对学生进行个性化指导，从而为学习能力较强的学生提供更丰富的知识和技能培养，为学习效果不理想的学生给予更多有针对性的帮助，也可以帮助学生减少学业压力[4]。

课程成绩预测的主要研究问题为输入特征和算法的选择，即针对特定的学习情境指定相关的影响因素作为特征，并使用适合的算法构建最优的预测模型对成绩进行预测。特征主要分为两类，即学习能力水平和课堂参与度。常用的预测算法包括多元线性回归、支持向量机、神经网络和逻辑回归等。例如，文献[5]将绩点、前导课成绩和平时作业成绩作为特征，比较多元线性回归、神经网络和支持向量机等回归算法预测物理力学课学生的成绩，发现支持向量机算法的准确率最高为87.5%;文献[6]利用逻辑回归及其改进的两种迁移学习算法，以学生每周慕课视频观看进度、每周作业完成进度和每周作业成绩作为特征，预测慕课学生是否通过，发现迁移学习算法LR?SIM准确率更高更稳定。文献[7]应用数据挖掘方法构建自适应第二外语在线学习系统，以中国台湾地区70名大学生的性别、个性和焦虑程度作为特征，预测其在线英语课的课程成绩，发现BP神经网络算法的预测效果更好。

从上述研究可以总结出，不同情境适用的特征和最优算法不同，因此课程成绩预测需要根据课程特点来选择特征，并对多种算法进行对比实验，构建出最优模型。为了全面地反映学生的学习情况，大学基础课的课程成绩预测需要从主观和客观两方面来选择特征。本文根据大学基础课的特点，选择绩点、相关前导课成绩、平时作业成绩和提问次数作为客观特征，选择个人兴趣作为主观特征，实现并对比课程成绩预测中常用且被验证效果较好的支持向量机（分为高斯核函数算法和多项式核函数算法两种）、BP神经网络和逻辑回归等算法。并引入加权投票机制，将预测准确率较高的高斯核函数支持向量机和BP神经网络算法进行集成，发现加权投票集成算法的预测准确率和平均查准率（Average Precision，AP） 最高。利用预测效果最佳的加权投票集成算法，本文构建了大学基础课的课程成绩预测模型，为教师开展个性化教学提供了参考，为大学基础课的课程成绩预测提供了一个有效的方法。

1  特征选取与模型构建

1.1  特征选取

影响大学基础课课程成绩的因素体现在客观和主观两个方面。依据文献[8]提出的模型，影响学生课程成绩的因素主要分为三个方面：过往学习能力、课程表现和对课程的主观态度。其中，学生的过往学习能力和课程表现属于客观因素，可通过客观记录的数据进行分析，对课程成绩起到了主要影响[6];学生对课程的主观态度属于主观因素，可通过问卷调研获取并分析，对课程成绩起到了次要影响[9?10]。因此，为了全面反映大学基础课学生的特征，准确预测大学基础课学生的课程成绩，本文从主观和客观两方面选择特征并进行分析。

1.1.1  客观因素

客观因素中，体现过往学习能力的因素有绩点、相关前导课成绩和学历等因素，体现课程表现的因素有提问次数、平时成绩和课堂活动参与度等因素。文献[5]通过对比验证了采用绩点、相关前导课成绩和平时作业成绩作为特征可以更好地预测大学基础课成绩。文献[11]分析了提问次数作为深入探究的表现对学生成绩的影响。在大学基础课中，绩点反映了学生在学习新课程之前已经具备的综合学习能力，对学生学习一门新的课程会产生较大的影响。相关前导课成绩反映了学生前导知识掌握情况，对新课程的成绩有较强的影响[12]，且时间相近的前导课成绩可以更准确地反映学生的前导知识水平[5]。平时作业成绩重点体现学生学习新课程的情况。提问次数反映了学生参与课程相关的深入探讨的频次及学生的学习积极性，对知识的理解程度具有较大影响。结合文献[8]的学生课程成绩模型和对大学基础课影响因素的分析，本文选取绩点、相关前导课成绩、平時作业成绩和提问次数作为大学基础课成绩预测的客观特征，如表1所示。

1.1.2  主观因素

主观因素中，体现学生对课程主观态度的因素主要有学习兴趣、自我效能感和学习动机等。文献[13]验证了学习兴趣对大学课程成绩具有较强影响。在大学基础课中，学习兴趣影响学生学习的主动性，主要分为个人兴趣和情境兴趣两类。与情境兴趣相比，个人兴趣作为学生在课前对课程内容产生的兴趣[14]，对学生的课堂表现、知识掌握、价值观和成绩均有更强、更长期的影响[15]。因此，本文选取学生的个人兴趣作为大学基础课成绩预测的主观特征。本文通过量表来测量个人兴趣，改编了文献[16]设计的初始兴趣（Initial Interest，即个人兴趣）问卷，设计出适用于大学基础课的5分制个人兴趣问卷。

1.2  模型构建

结合所选的主观和客观特征进行建模之前，需要确定预测模型的输出。课程成绩预测模型的输出主要分为是否通过课程、百分制分数和5分制分数三类。每类预测结果都有相应的应用。其中，5分制分数主要用于个性化教学。本文的研究目标是为教师开展个性化教学提供参考。因此，本文采用5分制课程成绩作为输出，将学生的百分制课程成绩根据区间划分为5个等级，如表2所示。

对5分制的课程成绩进行预测是一个多分类问题，需要通过分类算法求解。分类算法需要对分类器进行训练，并对分类器的超参数进行调优以得到最优的模型。本文对课程成绩预测常用的分类算法及其需要调整的超参数进行了分析。

1.2.1  课程成绩预测的分类算法

课程成绩预测常用的分类算法有支持向量机、逻辑回归和BP神经网络等。其中，支持向量机算法需要解决如下最优化问题[17]：

[        minw，b，ξ12wTw+Ci=1mξis.t.    y（i）（wT?（X（i））+b）>1-ξi，ξi>0] （1）

式中[C]为惩罚系数。支持向量机算法根据采用的核函数分为多类，其中，多项式核函数支持向量机的决策函数为：

[fk（X）=sgni=1mα（i）y（i）[X*X（i）+b]d] （2）

式中：[d]为多项式的阶;[b]为偏置系数。

高斯核函数支持向量机的决策函数为：

[fk（X）=sgni=1mα（i）y（i）exp-γX-X（i）2] （3）

式（1）～式（3）中：[γ]为构造高维特征的参数;[C]，[d]，[b]是支持向量机算法中需要调节的超参数。逻辑回归是经典的分类算法之一，其损失函数为：

[L（w）=i=1mlog（1+exp（-y（i）wTX（i）））+Cw2] （4）

逻辑回归需要调整超参数[C]，在最小化[Lw]的同时提高模型的泛化能力。不同于逻辑回归，BP神经网络加入了隐藏层的概念，通过反向传播算法重复调整权值和阈值来最小化损失函数的值。常用的BP神经网络为三层MLP（Multi?Layer Perceptron）[18]，需要调节隐藏层神经元个数[nhidden]来优化效果。

1.2.2  模型分析

本文将上述课程成绩预测常用的分类算法作为分类器，构建学生课程成绩预测模型，如图1所示。

模型的输入为5个特征，输出为5个成绩等级，是一个多变量、多分类模型。鉴于上述分类算法均适用于二分类问题，模型采用OvR方法将二分类问题转换为多分类问题进行求解。模型的分类器如式（5）所示：

[f（X（i））=Φ（X（i），y（i））] （5）

式中向量[X（i）]表示第[i]个样本的特征向量，如表3所示;[Φ]表示决策函数，根据采用的分类算法决定。向量[y（i）=][[y（i）1，y（i）2，y（i）3，y（i）4，y（i）5]T]表示第[i]个样本的实际分类结果，其中，[y（i）k∈{-1，1}k∈{1，2，3，4，5}];[f（X（i））]为模型判定第[i]个样本的分类结果，取值为[[f1（X（i）），f2（X（i）），][f3（X（i）），f4（X（i）），f5（X（i））]T]，其中，[fk（X（i））∈{-1，1}]且[k∈{1，2，3，4，5}]。

由于单个分类算法的预测能力是有限的，为了构建准确率更高的模型，本文使用投票法对分类算法进行改进。投票法是一种集成学习方法[19]，对多个分类算法的预测结果进行投票，将得票最高的结果作为最终预测结果，实现对多个分类算法的权衡，提高预测准确率。然而，不同子分类器的预测准确率不同。如果直接进行投票，则预测结果会受到预测误差较大的子分类器的影响。为了减弱这种负面影响，本文引入加权投票机制，将预测准确率较高的课程成绩预测分类算法进行加权投票集成，为预测准确率高的子分类器分配更高的权值，加强其对最终结果的影响，进一步提高预测准确率。预测准确率定义为：

[p（f（X（i）），y（i））=1mi=1m1（f（X（i））=y（i））] （6）

式中[1（x）]为指示函数。权值的定义如下：

[wl=pl（f（X（i）），y（i））l=1Lpl（f（X（i）），y（i））] （7）

式中：[pl]表示第[l]个子分类器的预测准确率;[L]为子分类器总个数。集成后的分类器的预测结果概率值为：

[P=l=1LwlPll] （8）

式中：[Pl]表示第[l]个分类器预测结果的概率，向量[P]中最大值对应的类别为集成算法最终的分类结果。为了验证加权投票集成算法的效果，本文结合所选主观、客观特征，分别将上述课程成绩预测常用的算法加权投票集成算法作为模型的分类器进行模型训练和调优，通过对比选择最优的算法构建大学基础课的课程成绩预测模型。

2  实验与讨论

2.1  数据收集与预处理

本文结合上述对特征选取和模型构建的分析，以北京某高校大学基础课面向对象程序设计（C++）的54名学生为研究对象，未对学生进行直接干预，通过收集学生的特征和期末成绩数据进行实验分析。

学生的客观特征通过教务系统和课程教师统计。其中，绩点和相关前导课成绩均采集自学校的教务系统。相关前导课成绩为百分制，绩点和平时作业成绩为5分制。平时作业成绩来源于课程教师的统计结果。本文采集的平时作业成绩以12次实验报告的成绩为准，统计情况如表4所示。

提问次数通过课程教师和助教进行统计。该C++课中学生对教师的提问通过在线社区Moodle、微信以及实验报告留言三种方式进行，因此本文统计了微信、Moodle和实验报告中每个学生提问的次数，以教学周为一个教学阶段进行收集，共计12次，统计结果如表5所示。其中，微信提问来源于学生与助教和教师的微信聊天记录，Moodle提问来源于学生在Moodle社区讨论区中的发帖与回复，实验报告提问来源于学生平时编程实验中实验报告的反思与讨论部分。

主观特征通过问卷计算得出。学生在课程第一周通过在线填写的方式完成该问卷。本文共收回54份有效问卷，以学生每道题目打分的均值作为该学生个人兴趣分值，其统计结果如表6所示。

鉴于分类算法对于特征间数值的差异较为敏感，因此需要在训练之前将特征进行归一化处理以防止某一特征因为数值较大在模型预测时占据主导地位。本文采用均值归一化的方法进行特征缩放，将特征的数值映射到区间[0，1]内，以便于获得更有效、可靠的模型。

2.2  模型训练与参数调节

本文以Python为编程语言编写各个算法，在macOS High Sierra环境中进行模型的训练和测试。实验以具有5个特征的648个样本作为输入，其中70%的数据用作训练集，其余30%的数据用作测试集，以预测准确率（Accuracy）作为衡量模型效果的指标之一，通过训练集训练出模型，利用该模型预测测试集样本的分类。实验在进行模型训练时利用Grid Search方法，通过10?fold交叉验证调节各个算法的超参数。各个算法调参结果见表7。

在调节超参数之后，实验计算了各个算法对5个成绩等级预测准确率的均值，如表8所示。其中，BP神经网络算法的预测准确率最高，其次是高斯核函数支持向量机算法，二者均达到90%以上的预测准确率;而多项式核函数支持向量机和逻辑回归的预测准确率较低。

本文选择预测准确率较高的高斯核函数支持向量机算法和BP神经网络算法作为加权投票集成算法的子分类器并计算其预测准确率，与其他四个模型的预测准确率进行对比，如图2所示。

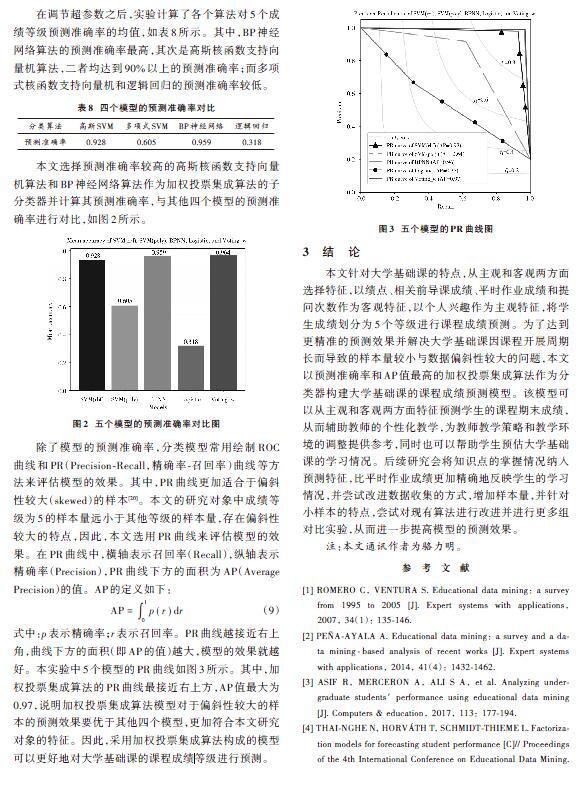
除了模型的预测准确率，分类模型常用绘制ROC曲线和PR（Precision?Recall，精确率?召回率）曲线等方法来评估模型的效果。其中，PR曲线更加适合于偏斜性较大（skewed）的样本[20]。本文的研究对象中成绩等级为5的样本量远小于其他等级的样本量，存在偏斜性较大的特点，因此，本文选用PR曲线来评估模型的效果。在PR曲线中，横轴表示召回率（Recall），纵轴表示精确率（Precision），PR曲线下方的面积为AP（Average Precision）的值。AP的定义如下：

[AP=01p（r）dr] （9）

式中：[p]表示精确率;[r]表示召回率。PR曲线越接近右上角，曲线下方的面积（即AP的值）越大，模型的效果就越好。本实验中5个模型的PR曲线如图3所示。其中，加权投票集成算法的PR曲线最接近右上方，AP值最大为0.97，说明加权投票集成算法模型对于偏斜性较大的样本的预测效果要优于其他四个模型，更加符合本文研究对象的特征。因此，采用加权投票集成算法构成的模型可以更好地对大学基础课的课程成绩等级进行预测。

3  结  论

本文针对大学基础课的特点，从主观和客观两方面选择特征，以绩点、相关前导课成绩、平时作业成绩和提问次数作为客观特征，以个人兴趣作为主观特征，将学生成绩划分为5个等级进行课程成绩预测。为了达到更精准的预测效果并解决大学基础课因课程开展周期长而导致的样本量较小与数据偏斜性较大的问题，本文以预测准确率和AP值最高的加权投票集成算法作为分类器构建大学基础课的课程成绩预测模型。该模型可以从主观和客观两方面特征预测学生的课程期末成绩，从而辅助教师的个性化教学，为教师教学策略和教学环境的调整提供参考，同时也可以帮助学生预估大学基础课的学习情况。后续研究会将知识点的掌握情况纳入预测特征，比平时作业成绩更加精确地反映学生的学习情况，并尝试改进数据收集的方式，增加样本量，并针对小样本的特点，尝试对现有算法进行改进并进行更多组对比实验，从而进一步提高模型的预测效果。

注：本文通讯作者为骆力明。

参考文献

[1] ROMERO C， VENTURA S. Educational data mining： a survey from 1995 to 2005 [J]. Expert systems with applications， 2007， 34（1）： 135?146.

[2] PE?A?AYALA A. Educational data mining： a survey and a data mining?based analysis of recent works [J]. Expert systems with applications， 2014， 41（4）： 1432?1462.

[3] ASIF R， MERCERON A， ALI S A， et al. Analyzing undergraduate students′ performance using educational data mining [J]. Computers & education， 2017， 113： 177?194.

[4] THAI?NGHE N， HORV?TH T， SCHMIDT?THIEME L. Factorization models for forecasting student performance [C]// Proceedings of the 4th International Conference on Educational Data Mining. Eindhoven： EDM， 2011： 11?20.

[5] HUANG S， FANG N. Predicting student academic performance in an engineering dynamics course： a comparison of four types of predictive mathematical models [J]. Computers & education， 2013， 61： 133?145.

[6] HE J， BAILEY J， RUBINSTEIN B I P， et al. Identifying at?risk students in massive open online courses [C]// Proceedings of the Twenty?ninth AAAI Conference on Artificial Intelligence. Austin： AAAI， 2015： 1749?1755.

[7] WANG Y， LIAO H C. Data mining for adaptive learning in a TESL?based e?learning system [J]. Expert systems with applications， 2011， 38（6）： 6480?6485.

[8] PARMENTIER P. La réussite des études universitaires： facteurs structurels et processuels de la performance académique en première année en medicine [D]. Belgium： Université Catholique de Louvain， 1994.

[9] DE BARBA P G， KENNEDY G E， AINLEY M D. The role of students′ motivation and participation in predicting performance in a MOOC [J]. Journal of computer assisted learning， 2016， 32（3）： 218?231.

[10] BAILEY T H， PHILLIPS L J. The influence of motivation and adaptation on students′ subjective well?being， meaning in life and academic performance [J]. Higher education research & development， 2016， 35（2）： 201?216.

[11] NEWMANN F M， MARKS H M， GAMORAN A. Authentic pedagogy and student performance [J]. American journal of education， 1996， 104（4）： 280?312.

[12] 黄建明.贝叶斯网络在学生成绩预测中的应用[J].计算机科学，2012，39（11A）：280?282.

[13] PINTRICH P R. The dynamic interplay of student motivation and cognition in the college classroom [J]. Advances in motivation and achievement， 1989， 6： 117?160.

[14] RENNINGER K A. Individual interest and development： Implications for theory and practice [J]. The role of interest in learning and development， 1992， 26（3/4）： 361?395.

[15] HIDI S. Interest and its contribution as a mental resource for learning [J]. Review of educational research， 1990， 60（4）： 549?571.

[16] HARACKIEWICZ J M， DURIK A M， BARRON K E， et al. The role of achievement goals in the development of interest： reciprocal relations between achievement goals， interest， and performance [J]. Journal of educational psychology， 2008， 100（1）： 105.

[17] CORTES C， VAPNIK V. Support?vector networks [J]. Machine learning， 1995， 20（3）： 273?297.

[18] GALLINARI P， THIRIA S， BADRAN F， et al. On the relations between discriminant analysis and multilayer perceptrons [J]. Neural networks， 1991， 4（3）： 349?360.

[19] DIETTERICH T G. Ensemble methods in machine learning [C]// International workshop on multiple classifier systems. Berlin： Springer， 2000： 1?15.

[20] DAVIS J， GOADRICH M. The relationship between precision?recall and ROC curves [C]// Proceedings of the 23rd international conference on machine learning. Pittsburgh： ACM， 2006： 233?240.

作者简介：陈佳明，男，硕士研究生，主要研究方向为人工智能与教育、数据挖掘。

骆力明，男，教授，硕士研究生导师，主要研究领域为智能教育、软件系统实现。

宋  洁，女，硕士研究生，主要研究方向为教育技术。