考虑微电网间能量互济的多微电网日前经济优化策略

田恬，王灿，陈思睿，余宏亮，梅世颐，李祥和

(1.新能源微电网湖北省协同创新中心(三峡大学)，湖北 宜昌 443002；2.三峡大学 电气与新能源学院，湖北 宜昌 443002)

煤、石油等一次能源的逐渐枯竭催生了大量分布式可再生能源接入配电网，而微电网作为分布式能源就地消纳的有效方式得到了迅速发展[1]。随着微电网的发展，局部区域内由部分联系紧密的微电网形成的多微电网系统开始出现[2]。多微电网相对于单微电网具有更高的运行稳定性和经济性，更有利于新能源的高渗透综合利用[3]。

研究并网多微电网的优化策略可实现对分布式发电单元的最优调度，在最大化微电网所有者经济效益的同时提高多微电网的运行稳定性[4]。文献[5]针对含储能设备的微电网，研究微电网内各发电单元之间协调发电的调度策略以实现微电网自身运行效益最大化。文献[6]针对风-光-柴-储微电网系统，建立了考虑设备损耗成本、运维成本、燃料成本的经济优化模型以优化分布式电源的经济性。但上述文献的研究对象均为单个微电网，且未考虑微电网并网协调运行的情况。文献[7-8]将多微电网与配电网视为不同利益主体分步优化，旨在保证新能源发电比例的同时，减少与配电网能量交互，同时保证多微电网系统的运行经济性。文献[9]针对含多微电网的配电网需求响应问题，建立了微电网优化模型和多微电网竞价博弈模型，以多微电网中各微电网运行成本最低为目标，得出多微电网最优调度的竞价策略。然而上述文献并未考虑多微电网系统中各微电网之间的能量互济问题。

为了求解大规模、分布式的电能资源带来的优化调度问题，学者们对求解算法展开了充分的研究。动态规划可以有效寻求到优化问题的全局最优解，但当决策变量的维数变大、阶段和状态也变多时，动态规划的计算时间和所需内存会极大增加[10]。文献[11]针对由光伏发电机、柴油发电机、风力发电机和储能电池组成的微电网的最优日前调度模型，提出了协调搜索与进化微分相结合的方法。文献[12]使用混合粒子群算法对微电网中可控分布式发电单元的出力安排进行优化，以提升微电网运行经济性。文献[13]针对考虑了系统运行安全约束的微电网环保经济调度模型，采用人工蜂群算法进行求解。文献[14]考虑了微电网的运行成本和环境污染排放成本，采用遗传算法对优化模型进行求解。上述群体智能算法具有简单、易于实现和收敛迅速的优点，因此在微电网领域受到了较多的关注；然而，群体优化算法均存在早熟收敛的问题。

针对上述问题，本文提出了一种考虑各微电网能量互济的多微电网日前经济优化策略。该策略在协调优化多微电网内分布式电源出力以降低发电成本的同时，通过各微电网之间的能量互济进一步降低多微电网的运行成本；此外，本文还提出了一种基于非线性变异算子的改进Jaya算法以提高优化模型的求解效率和求解精度。测试结果验证了所提出优化模型以及改进算法的有效性。

1 多微电网经济优化模型

多微电网系统结构如图1所示。系统中各微电网均连接于多微电网系统公共母线，并通过多微电网功率节点(point of common coupling，PCC)与配电网连接[15-18]。此结构一方面可实现多微电网系统与配电网的能量交互，另一方面可实现各微电网之间的能量互济。每个微电网中包含负荷(Load)并配备储能电池(battery，BAT)，且分布式发电单元由光伏(photovoltaic，PV)、风力机(wind turbine，WT)以及微型燃气轮机(microturbine，MT)组成。各微电网中央控制器(microgrid central controller，MGCC)控制微电网内各微电源的运行调度，多微电网中央控制器(multi-microgrid central controller， MMGCC)实现对系统内各微电网的整体管理。

图1 并网多微电网系统结构Fig.1 The structure of the grid-connected multi-microgrid system

1.1 分布式电源模型

分布式电源模型包括以下部分：

a)储能设备。本文选用应用较为广泛的蓄电池，考虑其运行维护成本和延长电池运行寿命，对其充放电功率和荷电状态(state of charge，SOC)进行了约束。

t时段微电网n中第i个储能电池运行维护成本

CBATn,i,t,om=kBATn,i,om|PBATn,i,t|.

(1)

式中：kBATn,i,om为t时段电池组n中第i个储能电池的运行维护成本系数；PBATn,i,t为其输出功率，正值表示放电状态，负值表示充电状态。

输出功率约束及SOC约束：

PBATn,i,min≤PBATn,i,t≤PBATn,i,max.

(2)

fSOCn,i,min≤fSOCn,i,t≤fSOCn,i,max.

(3)

式中：PBATn,i,min和PBATn,i,max分别为第n个电池组的第i个电池最小和最大输出功率；fSOCn,i,min和fSOCn,i,max分别为第n个电池组的第i个电池最小和最大荷电状态；En,i,t为t时段第n个电池组的第i个电池的总能量；En,i,C为第n个电池组的第i个电池的额定容量;ηn,i,ch和ηn,i,dis分别为第n个电池组的第i个电池充电和放电效率。

b)微型燃气轮机。燃料成本Cn,i,t,fuel、维护成本Cn,i,t,om和启停机成本CSU,n,i,t、CSD,n,i,t为：

Cn,i,t,fuel=an,iPn,i,t2+bn,iPn,i,t+cn,i.

(4)

Cn,i,t,om=kn,i,omPn,i,t.

(5)

(6)

式中:an,i、bn,i、cn,i为微电网n中微型燃气轮机i的燃料成本系数(对于微电网n第i个微型燃气轮机有an,i=0，cn,i=0)[19-20]；kn,i,om为其运行维护成本系数；Pn,i,t为t时该机组的输出功率；cSU,n,i、cSD,n,i分别为其单位时刻开停机成本；Yn,i,t为t时段的机组启停状态，0表示停机状态，1表示开机状态。

输出功率上下限约束、输出功率爬坡速度约束为：

Pn,i,min≤Pn,i,t≤Pn,i,max.

(7)

-Rn,i,downΔt≤Pn,i,t-Pn,i,t-1≤Rn,i,upΔt.

(8)

式中：Pn,i,min和Pn,i,max分别为微电网n中微型燃气轮机i的最小和最大输出功率；Rn,i,down和Rn,i,up分别为微电网n中微型燃气轮机i的最小和最大爬坡率。

1.2 目标函数

在考虑微电网间能量互济的条件下，并网多微电网日前经济优化模型以所有微电网总运行成本最低为目标，决策各分布式电源的出力、微电网与配电网间的交互功率以及各微电网之间的能量互济功率。并网多微电网日前经济优化模型目标函数

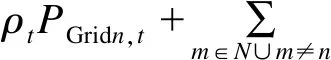
(9)

上述多微电网目标函数由4部分组成，分别为微型燃气轮机成本、储能电池成本、与配电网之间的购售电成本以及微电网之间能量互济成本。式(9)中：N为多微电网中的微电网集合；ρt为t时段与配电网的购售电电价；PGridn,t为微电网n在t时段的购售电功率，正值表示从配电网购电，负值表示向配电网售电；PEX,n,m,t为t时段微电网n与微电网m之间能量互济的功率，正值表示微电网n从微电网m购电，负值表示微电网n向微电网m售电，在t时段，PEX,n,m,t=-PEX,n,m,t。

1.3 约束条件

优化模型除了需要满足各分布式电源模型的约束条件外，还应满足微电网运行约束，如微电网电功率平衡约束和微电网联络线功率约束：

a)微电网n电功率平衡约束。约束式为

(10)

式中:PPVn,i,t和PWTn,i,t分别为t时微电网n中光伏i和风力机i的输出功率；PLoadn,t为负荷功率。

b)微电网n联络线率平衡约束。约束式为

PGrid,min≤PGridn,t≤PGrid,max.

(11)

式中PGrid,min和PGrid,max分别为联络线功率最小值和最大值。

2 并网多微电网调度策略

多微电网系统中的微电网在并网状态下相对于配电网或其他微电网而言，既有电源特性，又具备负荷特性[21]。系统中各微电网优先通过自身发电调度满足自身的负荷。微电网在自身发电能力不足时，可从配电网或其他微电网处购电以满足自身负荷；自身发电能力盈余时，可向配电网或者其他微电网售电。多微电网调度策略为：

a)多微电网中所有微电网自身发电能力均大于自身负荷时：在峰平时段，各微电网优先向配电网送电，再向储能装置充电；在谷时段，优先向储能装置充电，再向配电网送电。

b)多微电网中所有微电网自身发电能力均小于自身负荷时：在峰平时段，优先从储能装置获取电能，再从配电网购电；在谷时段，优先从配电网购电，再从储能装置获取电能。

c)多微电网中既存在发电能力大于用电需求大的微电网，又存在发电能力小于用电需求的微电网时,多电微电网优先向少电微电网送电，若多电微电网可满足少电微电网用电需求，则多电微电网的剩余发电能力可参照策略a)调度；若无法满足，则少电微电网可参照策略b)调度。具体并网多微电网调度策略如图2所示。

图2 并网多微电网调度策略Fig.2 Scheduling strategy for the grid-connected multi-microgrid

3 改进Jaya算法

3.1 Jaya算法简介

传统或经典的智能算法在求解复杂的优化问题时存在一定的局限性，这些限制主要与固有的搜索机制有关。RAO R V 在2016年提出的Jaya算法已被证明可以为无约束或有约束优化问题提供最优解[22]。已知基于种群的智能算法会受到特定算法的控制参数的影响，这些算法的性能取决于控制参数的变化。例如：粒子群算法的主要局限性在于需要对设置合适的特定算法的参数(如惯性权重w，加速因子c1、c2，最大速度vmax等)，来保证算法最优的运行状态，这些参数的合理调整是粒子群算法寻找最优解的关键，特定算法参数的变化会改变算法寻优的有效性，不适当地调整特定算法的参数会增加计算量或产生局部最优解；而Jaya算法无需任何特定算法的参数，概念简单且性能好，只需要通用控制参数(如种群大小，迭代次数)即可求解连续优化问题和离散优化问题的全局解，计算量小且一致性高。Jaya的基本原则为：在求解过程中总是试图接近最优解，远离最差解。设Xi,j,k是第i次迭代中第j个候选解的第k个变量的值，则在第i+1次迭代中将该值修改为

Xi+1,j,k=Xi,j,k+ri,j,1(Xi,j,best-|Xi,j,k|)-ri,j,2(Xi,j,worst-|Xi,j,k|).

(12)

式中：Xi,j,best和Xi,j,worst分别为变量k在第i次迭代中最优和最差的2个值；Xi+1,j,k为更新之后的值；ri,j,1和ri,j,2分别为第i次迭代中第j个变量在区间[0,1]中的2个随机数。若Xi+1,j,k能使目标函数获得更优的解，则Xi+1,j,k将被接受。

与其他仿生智能算法一样，该算法存在早熟收敛问题。在算法优化初期，种群中若出现了适应度远远优于当前种群普遍适应度的个体，会使该个体迅速在种群中占有相当大比例，导致种群多样性迅速降低，种群全局探索能力降低，最终使算法过早收敛于局部最优解。

3.2 基于非线性变异算子的Jaya算法改进

根据式(12)，Jaya算法生成的下一代解由当前解Xi,j,k、当前种群中最优解Xi,j,best和最差解Xi,j,worst共同决定；若算法出现早熟收敛，则Xi,j,best一定是局部最优解。为了降低Jaya算法陷入早熟收敛的概率，提升算法的性能，可使算法在迭代的不同阶段自动控制种群的进化方向；因此，本文提出采用非线性变异算子β将式(12)改写为：

Xi+1,j,k=Xi,j,k+βi,j[ri,j,1(Xi,j,best-|Xi,j,k|)-ri,j,2(Xi,j,worst-|Xi,j,k|)].

(13)

(14)

Δfi={|fi,1-fi,best|,|fi,2-fi,best|,…,

|fi,n-fi,best|}.

(15)

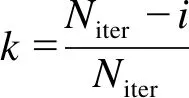
(16)

式中：βi,j为第i次迭代过程中第j个种群的的变异算子；βmax和βmin分别为变异算子的最大值和最小值，取βmax=0.9、βmin=0.4；fi,j为第i次迭代过程中第j个种群的适应度；fi,best为第i次迭代过程中最优种群的适应度；Δfi为第i次迭代过程中n个种群的适应度集合；Niter为最大迭代次数；k为迭代次数。

3.3 非线性变异算子对算法寻优过程的影响

本改进方法利用各种群相对于最优群体适应度的差值对变异算子进行动态调整，把变异算子的变化与种群的适应度信息关联起来，以便更加精确地调整变异算子。

当|fi,j-fi,best|较大时，即当前种群距当前最优种群的偏差较大，则利用式(14)赋予式(13)中变异算子βi,j较大的值，保证算法全局“探索”能力；当|fi,j-fi,best|较小时，即当前种群距当前最优种群的偏差较小，则利用式(14)赋予式(13)中变异算子βi,j较小的值，进而可以使算法在当前最优解附近更加精细地搜索最优解位置邻域，保证种群局部“开发”能力。通过以上调整变异算子的方法，可以增强算子的自适应性，更好地平衡算法的搜索行为，减少算法陷入局部极值的概率，提高Jaya算法的收敛性。

4 算例分析

4.1 算例系统概述

算例系统以图1所示的由2个微电网组成的并网多微电网为例进行分析。各微电网的配置见表1；各微电网微型燃气轮机参数见表2；各微电网储能设备参数见表3；配电网购售电实时电价见表4[23]，微电网间交易电价参考配电网购售电电价。各微电网的新能源出力曲线及日负荷曲线如图3所示[24]。其中，优化周期T取24 h，时间间隔为1 h，各微电网与配电网最大交互功率为100 kW，储能设备充放电效率均取0.95，SOC限制在0.1和0.9之间。

表1 各微电网配置Tab.1 Configurations in each microgrid

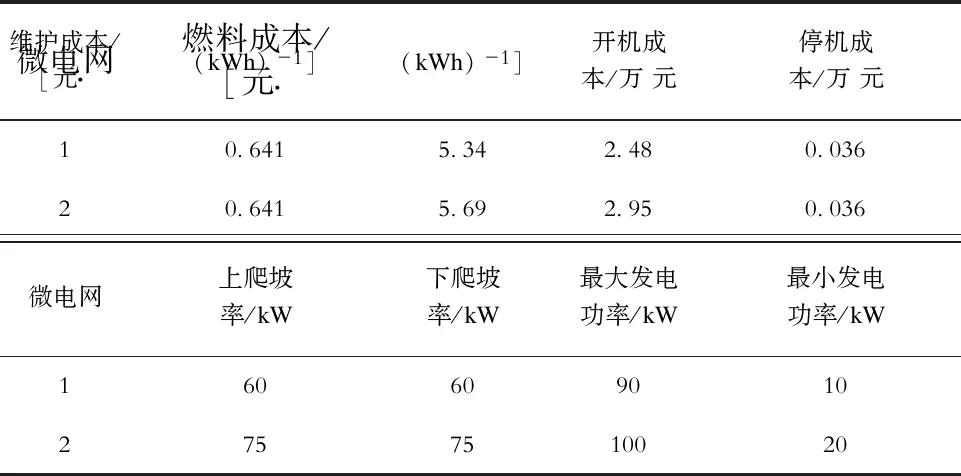
表2 微型燃气轮机参数Tab.2 Parameters of MTs

表3 储能设备参数Tab.3 Parameters of BATs

表4 实时交易电价Tab.4 Real-time trading price [元·(kWh)-1]

图3 各微电网新能源出力及负荷曲线Fig.3 New energy output and load curves of each microgrid

4.2 优化运行结果分析

采用本文所提出的优化策略，在考虑多微电网中各微电网时间能量互济以及微电网与配电网能量交互情况下，微电网1和微电网2的优化调度结果如图4和图5所示。图6为微电网之间的能量互济功率曲线以及各微电网与配电网交互功率曲线。

由图4和图5可以看出：在谷时段，各微电网均从配电网以较低的电价购电并为储能设备充电，并在峰时段向配电网售电以获取利润。储能设备的充放电行为在各微电网内起到了削峰填谷的作用；同时，微电网内优先使用清洁可再生能源满足负荷需求，微型燃气轮机仅在微电网内负荷水平较高的时段开启，降低了微电网运行成本，提升了新能源发电利用率。由图6微电网间能量互济曲线知：由于微电网2负荷水平较高，微电网1和微电网2之间存在能量互济，在满足多微电网内负荷需求时通过能量交易进一步提升了多微电网及各微电网自身经济性；各微电网与配电网交互功率遵循配电网调度，多微电网在谷时段从配电网购电填补其负荷低谷，在峰时段向配电网送电降低其负荷高峰。

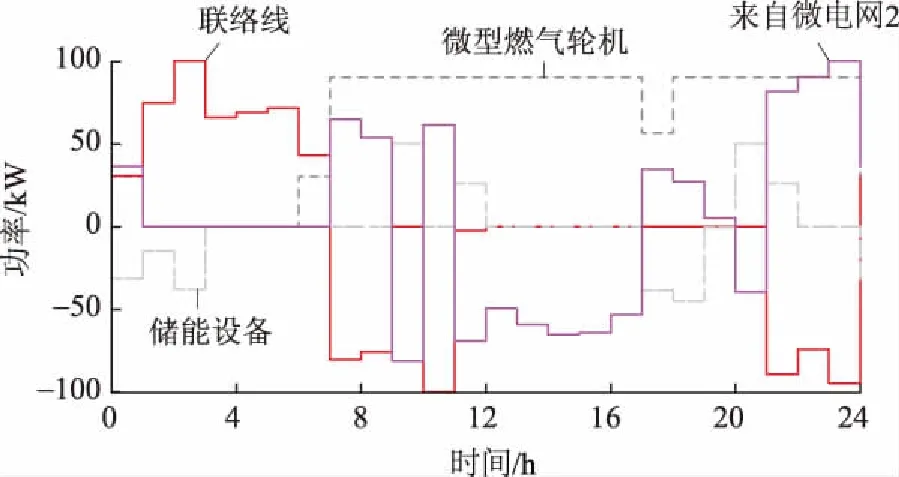
图4 微电网1优化调度结果Fig.4 Optimal dispatching results of microgrid 1

图5 微电网2优化调度结果Fig.5 Optimal dispatching results of microgrid 2

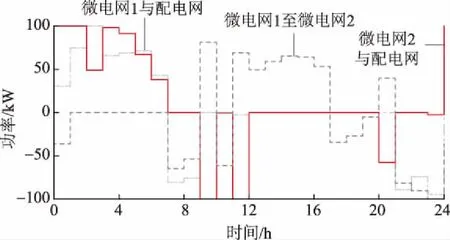
图6 微电网与配电网的能量交互功率以及各微电网的能量互济功率Fig.6 Interactive power of microgrid and distributed network and mutual power among microgrids

4.3 与各微电网独立运行时的对比分析

为了显示本文所提出优化策略的优越性，本小节将对各微电网独立运行方案进行综合对比分析。以微电网2为例，当各微电网之间不存在能量互济，即各微电网独立运行时，其优化调度结果如图7所示。

图7 微电网2独立运行时优化调度结果Fig.7 Optimal dispatching results of microgrid 2 in independent operation mode

图7与图5相比：当微电网2独立运行时，为了满足自身负荷需求，微型燃气轮机全天处于开机状态，而微型燃气轮机的长时间开机会对微电网的运行成本造成影响；同时，为了提升微电网经济效益并满足负荷需求，储能设备的充放电次数相对于图4增加了约70%，长时间重度使用储能设备将加快其老化速度，对微电网的稳定运行带来不利影响。

图8显示了2种调度策略下微电网1、微电网2以及多微电网整体的运行成本。由图8可知：在本文所提出的各微电网协调运行模式下，微电网1运行成本虽然略有增高，但微电网2的运行成本由1 834.373元降低至841.043元，多微电网的总体运行成本由2 709.145元降低至1 758.693元；相对于各微电网独立运行模式下的运行成本，微电网2的降幅达54%，多微电网的降幅也达到了35%，由此验证了本文所提出的多微电网日前经济优化策略的经济性。

图8 2种调度策略下运行成本对比分析Fig.8 Comparative analysis of operation costs of two dispatching strategies

4.4 改进Jaya算法收敛速度对比分析

采用标准Jaya算法和本文改进Jaya优化算法对优化模型进行求解，得到迭代收敛过程如图9所示。由图9可以看出：在迭代过程中，适应度均不断减小，与改进算法相比标准优化算法在迭代初期的收敛速度较慢；在迭代后期标准算法陷入了早熟收敛，而改进算法能够找到合适的全局最优解，从而说明改进算法具有较好的收敛性能和抗早熟能力。

图9 迭代过程中适应度变化曲线Fig.9 Fitness change curves during iteration

5 结论

本文针对并网多微电网日前经济运行问题，建立考虑微电网间能量互济及微电网与配电网功率交互的多微电网经济优化模型，并采用改进Jaya算法对优化模型进行求解，结果表明：

a)本文所提出的多微电网日前经济调度策略简捷合理、易于实施，且合理的调度策略不仅能够引导储能设备实现对微电网负荷的削峰填谷功能，还能使整个多微电网在并网运行时对配电网起到削峰填谷的作用。

b)通过协调微电网间能量互济及各微电网与配电网能量交易，调度策略的经济性得到了验证。相对于各微电网独立运行模式下的多微电网系统，本文所提出的策略不仅能大幅降低各微电网的运行成本，还能降低多微电网的总体运行成本。对于属于不同利益主体的微电网，各利益主体可在多微电网管理者的领导下签订相关协议。为了降低多微电网的整体运行成本，运行成本降低的几方可为其他利益主体给予一定的补偿，实现合作共赢。

c)本文所提出的改进Jaya算法能避免早熟收敛问题，跳出局部最优点，提高求解精度。

在本文的研究工作中，微电网之间的交易电价采用同时段的配电网购售电电价。为了进一步提高优化模型精度，在今后的研究工作中，将针对微电网交易定价机制进行详细研究。