单立柱堆垛机有限元振动分析

2

1.同济大学 中德学院 上海 201804 2.同济大学 机械与能源工程学院 上海 201804

1 研究背景

近年来,新物流概念的发展、全球市场的兴起，以及消费行为的改变,对物流运输效率提出了更高的要求。单立柱堆垛机是现代物料搬运技术的重要组成部分,在工厂内部物流中发挥着重要作用[1]。为了保证物流运输的高效率和短周期,堆垛机必须以尽可能高的速度和加速度工作,但运行过程中的加减速都会激发低频振动[2]。此类振动会造成堆垛机定位精度不准,定位效率及平稳性能降低,严重时甚至会产生碰撞,损伤堆垛机、货物和立体仓库货架,影响使用寿命。单立柱堆垛机在巷道方向运动时,只有当立柱的振动位移被控制在允许范围内时,货叉才能安全地抓取和存储货物。

综合目前对单立柱堆垛机振动特性的研究现状,主要有对堆垛机结构和材料优化的研究[3-7],以及对实际堆垛机产品或其替代模型的动态试验分析[8-9]。笔者基于ANSYS Workbench软件对单立柱堆垛机进行了有限元建模,对运行状态下的单立柱堆垛机进行了仿真分析,提出了加减速对振动影响程度的比较方法,并对不同加减速策略的振动激励效果进行了对比分析。

2 有限元建模

笔者的研究对象为某公司生产的托盘式单立柱堆垛机,并配有双伸缩货叉。建模时首先对模型结构进行合理简化,去除各种电气装置、吊舱等与分析无关的零散部件。再进行几何简化,删除整体模型中对刚度和强度影响不大的几何特征。

将几何模型装配体在ANSYS Workbench软件中进行处理后,得到图1所示单立柱堆垛机有限元模型。图1中实心圆点为质量点,与对应零件采取多点约束的方式进行耦合。在该有限元模型中，模型类型可以分为三类,见表1。

柔性实体中立柱的材料为结构钢。笔者应用Design Modeler中的概念建模工具对钢丝绳进行线体建模,并生成为link 180单元,使其能完全模拟绳索只传递拉力、不传递压力的特性。提升机构至上横梁滑轮及滑轮之间的钢丝绳以力F的形式简化,并以边界条件的形式施加于有限元模型上。

该模型中下横梁和地面导轨的约束以运动副的形式来体现,下横梁具有沿X轴方向，即巷道方向的平移自由度和绕X轴的转动自由度。立柱上横梁相对上导轨的运动副具有三个自由度,分别为沿X轴方向和Z轴方向的平移自由度，以及绕X轴的转动自由度。伸缩货叉相对于载货台具有沿X轴方向的移动自由度。载货台与立柱导轨采取不分离的方式连接,有且只有沿Z轴方向，即导轨方向平移的自由度。立柱与上下横梁采用绑定连接。

▲图1 单立柱堆垛机有限元模型

表1 模型类型

3 有限元仿真分析

3.1 加速度激励下立柱振动形式

对单立柱堆垛机仿真模型沿巷道方向施加常值加速度,一段时间后撤去,观察立柱的振动情况，可得加速度对立柱的振动激励，如图2所示。单立柱堆垛机在时间点t1获得一个稳定常值加速度后,由于惯性力作用,立柱会产生与单立柱堆垛机整体运动方向相反的振动位移，即堆垛机立柱顶端的水平位移相对于整体堆垛机水平位移的动态偏离。这个振动位移幅值在起始阶段最大,随后由于阻尼作用,会在较长的加速时间段内衰减，并在趋近于时间点t2时形成一个稳定的振动位移W2,此段振动衰减过程称为运动引起的变形。W2的大小受到所施加的加速度大小、立柱刚度、载货台工作高度，以及单立柱堆垛机质量分布和大小的影响。

▲图2 加速度激励下立柱振动位移

当加速一段时间后至时间点t2达到理想速度，即最大速度时,移除加速度。此时立柱会继续受到惯性力的激励并产生新的振动,振动幅度会随着时间的变化而逐渐衰减,经过一段时间Δt后至时间点t3衰减至振动位移W1。设W1为定位精度,此段振动衰减过程称为剩余变形。在笔者的研究过程中,剩余变形阶段中的最大振动位移幅值及衰减至W1所需要的定位时间是对比的重点。

根据单立柱堆垛机在完整的三段直线加减速情况下的振动激励，可得直线加减速对立柱的振动激励，如图3所示。由图3可以看出，由于加速度的突变,对于加速、匀速、减速至最后的静止阶段,每个阶段在过渡的过程中都会产生振动的阶跃式变化。

▲图3 直线加减速对立柱振动激励

3.2 S形加减速与直线加减速比较

常见的加减速有S形加减速和直线加减速两种[10]。在S形加减速曲线中,根据加速度和速度能否保持峰值状态又可分为七段S形加减速和五段S形加减速，即加速度在整个运动过程中的变化次数分别为七次和五次。根据表2中单立柱堆垛机仿真模型运动参数,构造如图4所示直线加减速及S形加减速曲线模型。

对单立柱堆垛机有限元模型采用图4所示三种加减度模型进行仿真分析,为了获得最大振幅和最长振动周期便于对比研究,仿真中将载货台设置在最危险位置，即立柱顶端,并保持满载状态。

表2 单立柱堆垛机仿真模型运动参数

三种加减速曲线下立柱振动位移的对比如图5所示。由图5可以看出，虽然采用S形加减速策略在完成相同行程时所需要的时间略有增加,但是抑振情况要优于三段直线加减速。而在五段S形加减速策略中,由于加速度和速度都不能保持峰值,因此效率较其余加减速策略都低。

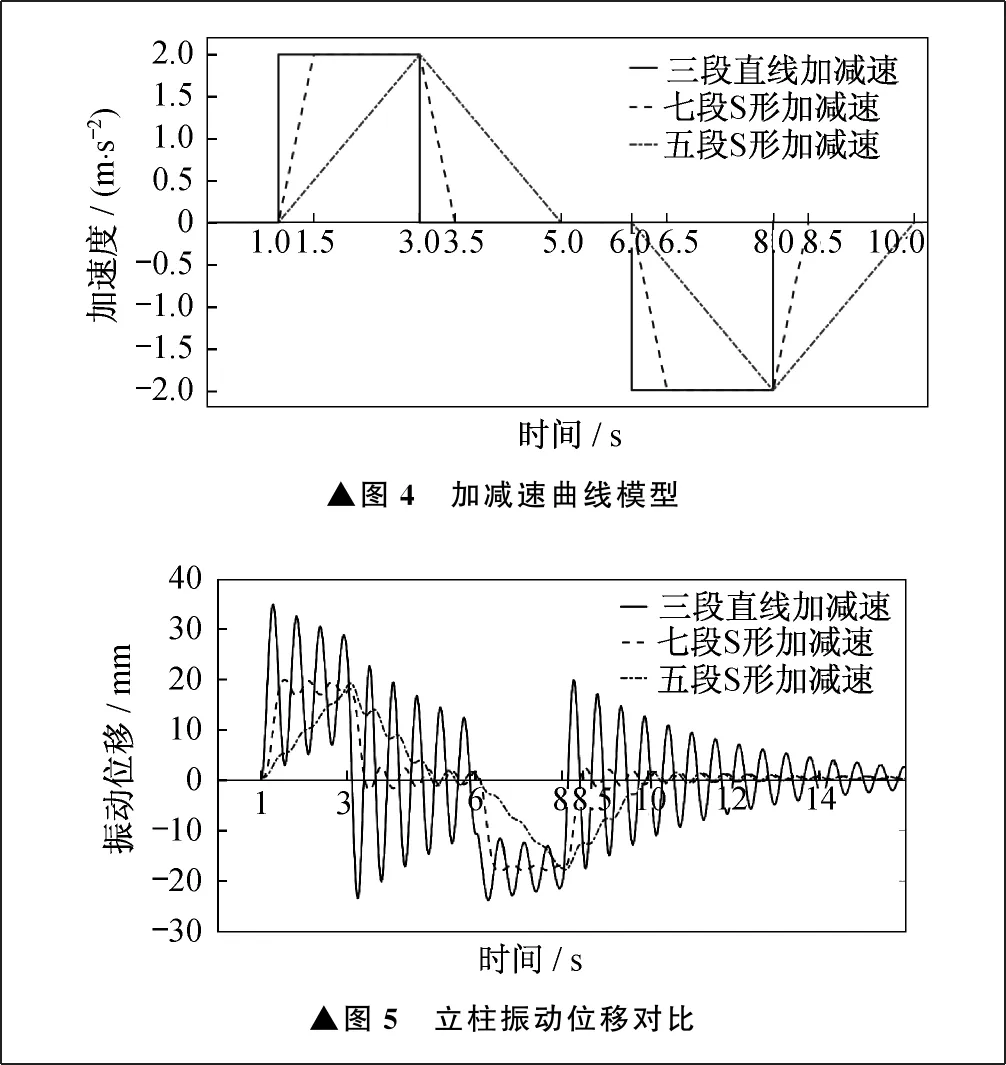
▲图4 加减速曲线模型▲图5 立柱振动位移对比

由上述仿真对比结果可以看出，不平滑的加速度曲线，即不连续的加加速度曲线会给单立柱堆垛机带来振动激励。运动过程中，在达到最大加速度和最大速度的基础上,为了提高加速度曲线的平顺度,基于连续的加加速度曲线构造加减速曲线是一种可行策略。

3.3 十五段S形加减速策略

基于上述分析,笔者构造了图6所示十五段S形加减速曲线。加速度在加加速阶段、减减速阶段、减加速阶段和加减速阶段表现为一条连续光滑的二次曲线,加加速度在上述四个阶段为线性可变值，因此速度、振动位移与时间分别是三次曲线和四次曲线的关系。

采用十五段S形加减速策略代入有限元模型进行仿真计算,并与七段S形加减速策略下立柱振动位移进行对比，如图7所示。四种加减速曲线定位效率比较见表3。在定位距离为20 m、定位精度W1为±1 mm时,采用十五段S形加减速曲线,定位所需要的时间为8.5 s,相比采用七段S形加减速曲线所需的时间10 s,定位效率提高了15%，且在剩余变形阶段中最大振动位移减小了37%。

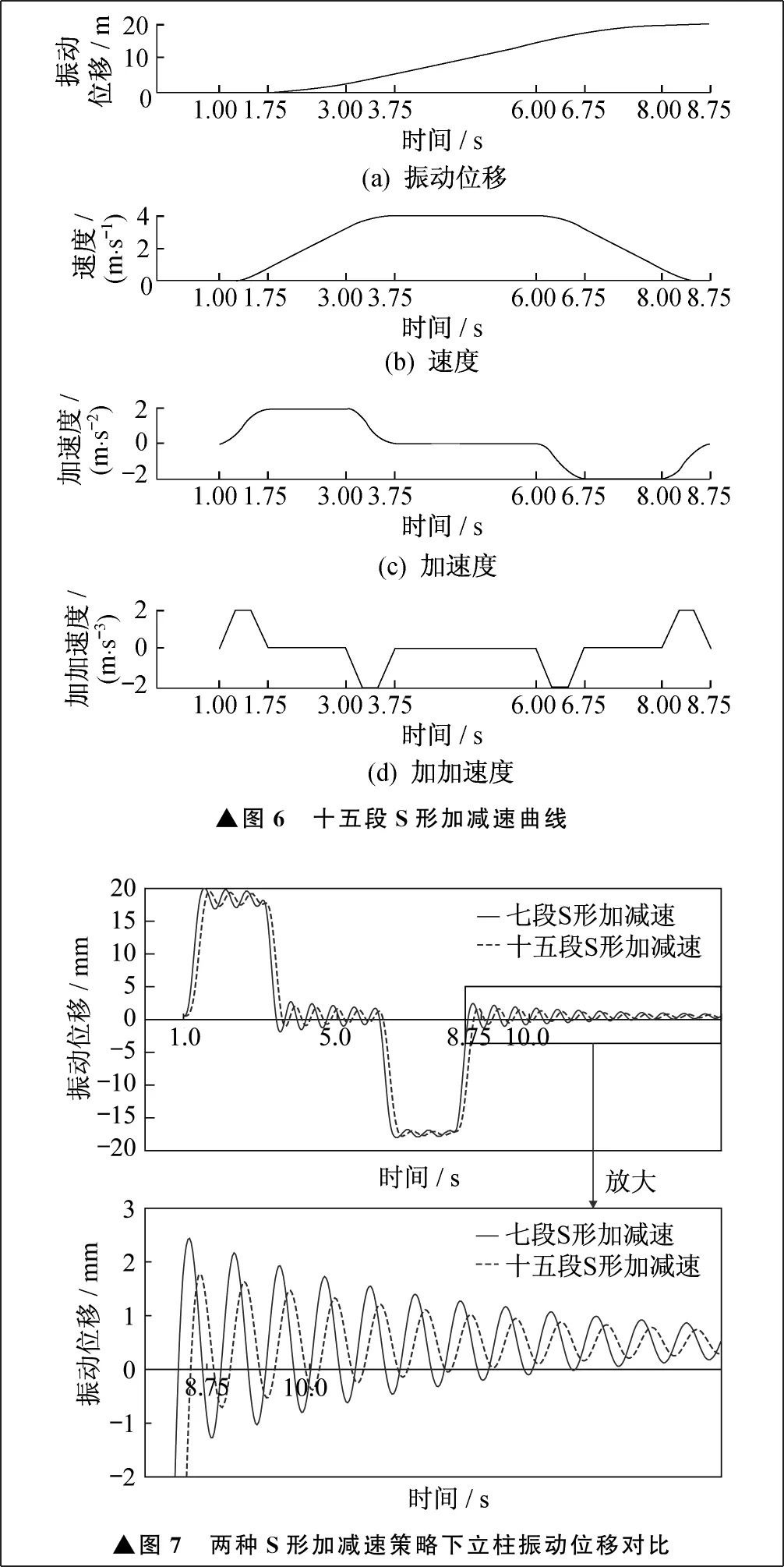
▲图6 十五段S形加减速曲线▲图7 两种S形加减速策略下立柱振动位移对比

4 结束语

根据仿真结果,使用基于连续加加速曲线构造的十五段加减速策略，可以有效抑制单立柱堆垛机立柱的振动情况,并缩短定位时间,提高定位效率。

表3 定位效率对比

笔者建立的单立柱堆垛机有限元仿真模型也具有一定的通用性,通过修改质量点的质量大小和位置，可用于模拟其它型号堆垛机。