跨声速风洞高速段一体化数值模拟研究
2020-03-03杨小川王运涛洪俊武黄知龙孙运强江雄
杨小川,王运涛,洪俊武,黄知龙,孙运强,江雄
(1.中国空气动力研究与发展中心 计算空气动力研究所,绵阳 621000)
(2.中国空气动力研究与发展中心 设备设计及测试技术研究所,绵阳 621000)
0 引 言
随着航空航天飞行器逐渐步入精细化设计的时代,特别是追求高亚声速经济巡航的民航客机以及跨声速高机动特性的战斗机,高性能跨声速风洞的需求日趋紧迫[1]。
目前,全世界有两座高性能跨声速风洞,分别是美国NTF(1983年第一次运行)和欧洲ETW(1993年第一次运行),投资分别为同时期的8 500万美元和5.62亿马克,由于ETW较NTF晚十年建设,在某些指标上更为先进。关于建设ETW跨声速风洞的起因,其推动力来自于1968年9月AGARD流体力学专家座谈会,会上报道了发生在19世纪60年代出现的众多跨声速空气动力学问题,如跨声速飞行面临的阻力剧增及焦点后移等气动问题[2]。同时,跨声速风洞能模拟真实飞行雷诺数,得到更为精准的试验数据供设计参考,如C-141飞机在超临界状态下,超临界机翼升阻和力矩特性对雷诺数特别敏感,真实飞行与风洞试验结果在机翼中部站位的激波位置相差近20%弦长[3],而超临界翼型和机翼设计技术又是现代跨声速运输类飞机气动力设计中最重要的关键技术之一[4],因此高性能跨声速风洞对现代飞行器设计意义重大。
对于跨声速状态而言,风洞试验段模型主要面临三个问题:①激波/膨胀波壁面反射;②气流拥塞;③相对自由来流的气流变化。因此跨声速风洞设计的关键在于消除/抑制上述物理问题,进而发展了槽壁或孔壁等技术,以及驻室和抽吸气等辅助手段[5]。关于跨声速状态风洞试验,直到1945年还没有可行的方案使试验段马赫数大于0.9。随后,Wright发展了一种纵向槽壁理论模型,用于消除试验段壁板和开口区域边界层干扰,并于1946年在安装有槽道试验段的风洞中获得成功,试验段马赫数达到跨声速范围,该成果很快应用到兰利的8和16 ft(1 ft=0.304 8 m)高速风洞中[2]。
在风洞数值模拟研究方面,国外,M.Kohzai等[6]采用渗透边界对跨声速风洞试验段进行支撑系统干扰模拟,并与试验结果进行对比;B.Goffert等[5]采用三维Euler方程对跨声速风洞中的翼型进行壁板有无开槽影响研究,并与试验结果中翼型压力系数分布、PSP分布及三维效应进行对比,其中开槽计算结果与试验吻合较好;S.A.Glazkov等[7]采用98万网格对简化的单槽道试验段模型进行三维粘性模拟,模型包括扩张角0.55°的槽壁、7°外开角的再导入调节片(或称指片Finger Flap)以及驻室,并与T125风洞试验进行对比分析,发现试验中存在明显的横向流动,而采用单槽道试验段计算结果无横向流动;A.R.Gorbushin等[8]首次采用具有低温求解模块的EWT-TsAGI软件对ETW风洞进行了带CRM模型的高速段一体化模拟(计算网格包括风洞试验段、槽壁、再导入调节片、驻室、弯刀尾撑机构以及CRM模型等部件,半模网格量达到1.7亿),该软件考虑了低温增压状态下氮气的真实气体效应,计算得到的试验段下壁面压力分布与试验值吻合较好。
国内,范洁川[9]对低速风洞洞壁干扰进行了大量研究,并得到合理的开闭比和开槽形式等参数;丛成华等[10]采用三维数值模拟方法对不同抽气量、抽气口位置以及壁板厚度、驻室容积、开闭比及槽型等参数进行对比分析,得到不同条件对跨声速试验段流动的影响情况;Qu K等[11]采用雷诺平均N-S方程对二维翼型进行有无开孔情况下的壁面干扰分析,并对不同孔壁高度和开孔率进行研究;刘光远等[12]对不同孔壁开孔率、引射缝、扩开角等状态下试验段核心流均匀性进行研究,得到了大型跨声速风洞试验段壁板参数影响的主要规律;江雄等[13]采用基于ARK方法模拟氮气低温高压真实气体效应的RANS求解软件,对典型运输机构型DLR-F6进行低温真实气体效应影响研究,结果显示真实气体效应引起的气动力差异相对雷诺数效应很小。上述研究对于提高我国跨声速风洞试验段设计能力起到推动作用,但关于跨声速风洞高速段一体化的复杂问题的研究仍相对较少。
本文采用中国空气动力研究与发展中心自主研发的“亚跨超CFD软件平台”(TRIP3.0)[14-15],对某跨声速风洞回路高速段进行一体化数值模拟初步研究,控制方程为雷诺平均N-S方程,采用有限体积法离散控制方程,空间方向无粘项离散采用MUSCL-Roe格式,湍流模型运用SST湍流模型。初步得到数值计算收敛评判方法以及不同初始条件和槽道扩张角对试验段流场品质的影响,并对槽道流动进行分析。
1 计算方法
1.1 控制方程
假设采用惯性笛卡儿坐标系,忽略彻体力,则Euler/Navier-Stokes方程为

(1)
其中,


式中:ρ,u,v,w,p,e和h分别为密度、x,y,z方向的绝对速度分量、压力、内能和总焓。
当NVIS=0时,方程形式为Euler方程;当NVIS=1时,方程形式为N-S方程。
1.2 拼接网格方法
拼接网格也称滑移网格(Sliding Mesh),多用于“剪刀缝”或构型复杂的计算外形以及存在多体相对运动的物体,与重叠网格功能类似。其基本特点是:存在拼接的网格块之间相互独立,在交接面上网格可不对应,即不用考虑相邻块的拓扑关系,仅需要网格块之间存在交接面。为了保证计算的收敛性,交界面两侧网格尺度及分布应尽可能接近。
拼接采用面积加权的线性插值方式,保证两侧通量守恒。该计算策略降低了网格的生成难度,特别是结构网格生成。另外,拼接面两侧网格块不需要进行对应,对单侧网格块进行加密,另一侧网格块不受影响,使计算网格规模适当降低[16]。
1.3 边界条件
在边界条件方面,物面上采用无滑移条件,入口边界给定总压P0,取稳定段总压;出口边界给定背压Pb,且存在
σ=Pb/PIN
(2)
式中:PIN为入口静压或方程无量纲化静压;σ为出口压比。
根据试验马赫数,不断更改扩压段出口背压,使试验段实际马赫数与试验马赫数相近。
2 算例验证
采用非对称平板扩压器(Plane Asymmetric Diffuser,简称PAD)算例,进行内流场中分离与再附等粘性流问题验证,主要对计算湍流模型进行考核。关于非对称平板扩压器有较多试验,而扩张角由10°减小到8.5°,能减小分离区域,获得更典型的流动二维性以及稳定的分离和再附点,即非定常效应影响更小[17],故选取8.5°扩张角非对称平板扩压器作为研究对象。
算例中扩压器共分为三段:入口段、扩压段以及出口段,扩压段扩张角为8.5°。该扩压器入口来流速度约为19.48 m/s,雷诺数为40 000。入口段、扩压段以及出口段流向的网格分布分别为121、165和137个点,展向和法向网格分布为69×81,采用全对接结构网格,网格量约为230万。
扩压段截面速度分布与试验结果对比如图1所示,可以看出:计算值与文献[17]中试验值吻合较好,在x/H为15~25截面靠近倾斜壁板一侧区域存在差异,主要是该区域存在较大范围分离所致。
扩压段截面速度云图及流线如图2所示,分离区域如图3所示,可以看出:计算得到的分离点在x/H=9附近,再附点在x/H=31附近,这与试验结果相吻合,初步验证了计算方法的可行性;同时计算得到的分离区域较试验值均偏小,这可能和网格尺度、湍流模型等因素有关。
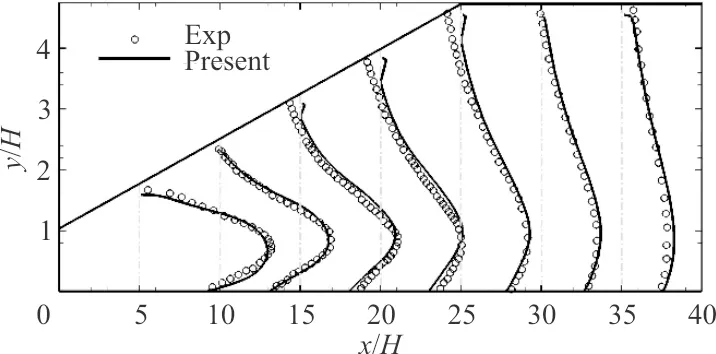
图1 扩压段截面速度分布

图2 扩压段截面速度云图及流线

图3 扩压段分离区域示意图
3 计算对象及网格
3.1 计算对象
计算对象为某跨声速风洞回路高速段外形,包括稳定段、收缩段、喷管、试验段、二喉道、扩张段以及包围试验段的驻室。试验段采用槽壁构型,上下各6根条型槽壁,左右为实壁,包含弯刀、尾撑以及再导入调节片。计算中再导入调节片偏角0°、二喉道开角为0°,且驻室及扩压段无抽吸气处理,同时尾撑头部为圆锥体。
3.2 计算网格
在实际计算中需对真实风洞进行适当简化,主要在弯刀和驻室两个部分进行简化。将伸入驻室的部分弯刀适当扣除,同时将驻室简化为轴对称外形,且驻室前段空间适当减小。计算主要针对跨声速状态,并对不同时间步长、初始化条件和槽壁扩张角进行分析。
计算网格为结构网格,由于模型可视为上下和左右对称,因此选取四分之一模型网格作为计算域。为了保证计算精度,特别是计算槽道粘性作用,需在壁面和槽道生成附面层网格,而风洞流道内存在圆方相互转换以及槽壁台阶等因素影响,采用全对接结构网格生成难度大,故选取拼接网格方法进行处理。
计算网格由三个独立的全对接结构网格组成,网格拼接处理示意图如图4所示,其中三个网格区域共进行两次拼接处理,分别位于喷管与试验段结合处和试验段与二喉道结合处。图中Cross Field#2为试验段及对应驻室部分网格,网格量约为5 200万;Cross Field#1为稳定段、收缩段、喷管段及对应驻室部分网格,网格量约为470万;Cross Field#3为二喉道、扩压段及对应驻室部分网格,网格量约为390万。整个计算域网格量约为6 060万,由于槽道流动是跨声速风洞气动设计的关键之处,试验段网格在槽道拐折等变化较大处均进行适当加密,试验段网格示意图如图5所示。

图5 跨声速风洞构型网格示意图
4 结果分析
对管道流动而言,收敛依据较难判断,通常采用出口流量或流场参数变化等作为收敛参考,但对于风洞而言,试验段流场均匀性是评判风洞品质的核心参数,因此本文选取试验段监测点作为收敛判断依据。风洞对称面示意图如图6所示,在图中模型区域轴向位置近似选取一前一后两个固定点,即监测点Point 1和监测点Point 2,计算中实时输出两个监测点的马赫数,通过两点马赫数变化量以及两者马赫数差量变化作为判断依据,X1~X3为流向x方向截面站位位置分布。

图6 对称面计算监测点及截面站位位置示意图
风洞试验段X站位截面及槽道位置示意图如图7所示,其中虚线区域为模型区域,中心点为中轴线处点,60%点为模型区域对角线上60%处点,用于表示中心线或60%站位处轴向马赫数分布情况。
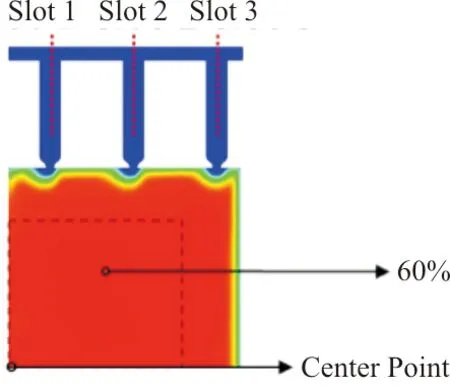
图7 试验段横截面参考点位置及槽道位置示意图
4.1 收敛步数
为了保证计算结果接近收敛解,选取两个典型状态作为参考,分别为亚声速状态和跨声速状态。通过分析模型区前后两个监测点马赫数的变化以及两者马赫数差量变化,来判断计算收敛情况。
4.1.1 亚声速状态
计算状态:试验段Ma=0.58,再入调节片偏角0°,上下槽壁,槽壁扩张角0.0°,计算初始化条件为Ma=0.0,为了尽可能保证计算的收敛性,定常计算迭代步数达到200万步。
监测点马赫数随时间步变化曲线如图8所示,模型区马赫数从速度为0.0开始逐渐加速到Ma=0.58附近,从图8(a)可以看出:在10万步左右监测点马赫数基本达到稳定值,在10万~200万步的计算历程中,马赫数均在小幅波动;监测点马赫数差量在10万前逐渐缩小到0.005 5附近,且在10万~200万步的计算历程中微幅波动;模型区域监测点1较监测点2马赫数大,仅为马赫数差量约0.005 5。从图8(b)可以看出:监测点1稳定在Ma=0.583 3附近波动,波动幅度达±0.36%;监测点2稳定在Ma=0.578 0附近波动,波动幅度达±0.35%;两个监测点马赫数差量稳定在0.005 5附近,波动基本维持在0.005 0~0.006 0之间,整个模型区核心流马赫数分布均方根偏差为0.001 84。

(a) 计算历程

(b) 马赫数波动
4.1.2 跨声速状态
计算状态:试验段Ma=0.94,再入调节片偏角0°,上下槽壁,槽壁扩张角0.3°,计算初始化条件为Ma=0.9,为了保证计算收敛性,定常计算迭代步数达到60万步。
监测点马赫数随时间步变化曲线如图9所示,模型区马赫数从速度Ma=0.9开始逐渐加速超声速后又回到Ma=0.94附近,从图9(a)可以看出:在12万步左右监测点马赫数差量基本达到稳定值,监测点马赫数差量逐渐缩小并稳定在0.008 5附近,且12万~60万步的计算历程中微幅波动;模型区域监测点1较监测点2马赫数大,马赫数差量约为0.008 5。从图9(b)可以看出:两个监测点在12万步后马赫数基本稳定;监测点1稳定在Ma=0.944 1附近波动,波动幅度达±0.17%,监测点2稳定在Ma=0.935 6附近波动,波动幅度达±0.17%;两个监测点马赫数差量稳定在0.008 5附近,波动基本维持在0.006~0.011之间,整个模型区核心流马赫数分布均方根偏差为0.002 1。

(a) 计算历程
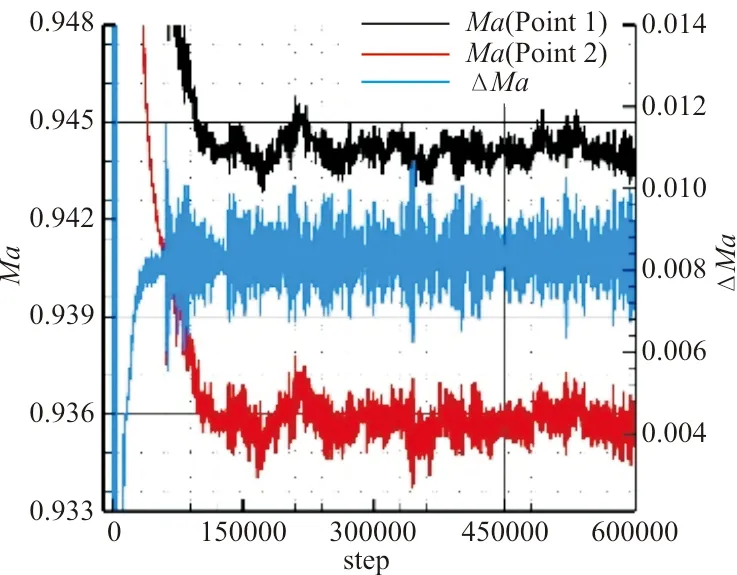
(b) 马赫数波动
通过对上述两种状态的收敛性分析发现:对于试验段马赫数为低亚声速状态,计算在10万步左右基本收敛;对于试验段马赫数为跨声速状态,计算在12万步左右基本收敛。为了保证计算收敛性,后续计算迭代步数均选取20~40万步。
4.2 初始条件
对比状态:计算域初始化流场中马赫数赋值分别为Ma=0.0、Ma=0.9,其他条件均相同,即再导入调节片偏角0°,上下槽壁扩张角0.3°,出口背压相同,计算步数均为23万步。
在上述两种不同初始化流场马赫数条件下,对称面及Slot 2槽道截面马赫数云图、X站位马赫数云图以及槽道流动细节对比情况分别如图10~图12所示,其中图12在x轴方向坐标尺度适当压缩,以便于观察流线方向。

(a) Ma=0.0

(b) Ma=0.9

(a) Ma=0.0
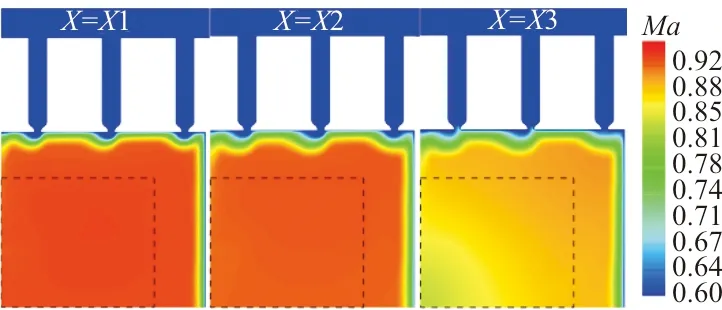
(b) Ma=0.9

(a) Ma=0.0

(b) Ma=0.9
从图10~图12可以看出:①两种初值条件得到的马赫数分布,在对称面、槽道截面以及X站位处基本相同;②气流从稳定段开始经过声速喷管逐渐加速到跨声速,并在试验段形成范围较大较稳定的跨声速区域,经弯刀尾撑形成局部加速区,同时在二喉道附近减速到亚声速,并继续在扩压段减速;③气流高速区基本维持在试验段内,驻室和槽道未出现明显的高速气流;④试验段槽道附近出现明显的横向流动;⑤槽道内低速气流进入试验段,同时气流从驻室流向槽道和试验段,然后在尾撑弯刀附近流回槽道,最后经过再入调节片流回二喉道或驻室,该现象可能是驻室无抽吸气处理,导致驻室压力过大,将槽道气流“压入”试验段所致。
两种不同初始化流场马赫数条件下,两个监测点马赫数收敛曲线以及试验段轴向马赫数分布情况如图13所示,其中黑线和红线分别代表模型区中心线前后两监测点马赫数,蓝线代表两者之差,可以看出:当初值为Ma=0.0时,模型区速度由0.0开始逐渐增大并稳定在0.9附近,两点差量在5万步基本收敛,且收敛前抖动剧烈,收敛后抖动大幅减小且稳定在0.01内;当初值为Ma=0.9时,模型区马赫数先由0.9剧增到1.53,然后减小并稳定在0.9附近,两点差量基本稳定在0.01内且始终保持小幅抖动;从收敛速度来看,初值为Ma=0.0时,计算到5万步接近收敛,而初值为Ma=0.9时,计算在3万步左右收敛,即初值Ma=0.9较初值Ma=0.0计算收敛速度更快。
在图13(c)试验段轴向马赫数分布上,两种初值条件得到的收敛后结果基本相近,初值Ma=0.0得到的模型区马赫数较初值Ma=0.9变化趋势一致,且初值Ma=0.0条件得到的马赫数略高,这可能是因为管道流动,特别是跨声速槽道流动复杂,分离区域较多,气流流动对计算因素变化反应敏感所致。模型区的中心线马赫数差量即为前后两个监测点差量,60%站位点(如图7所示)轴向马赫数分布较中心线分布更为平缓,马赫数差量较中心线更小,这主要是模型区后方存在尾撑,而尾撑对中心线方向影响较60%站位点更明显,且越靠近尾撑,干扰越明显。

(a) Ma=0.0

(b) Ma=0.9

(c) 试验段轴向马赫数分布
通过对比分析,得到两种初值条件对收敛结果总体影响较小(试验段马赫数存在一定差异),特别是各截面流场分布和槽道流动方向上,两者结果基本相同,同时两种初值条件均在5万步前收敛,5万步到23万步变化很小,且两者前后监测点马赫数差量均在0.008 5附近。差异之处在于:①收敛速度。初值Ma=0.9状态在3万步收敛,而初值Ma=0.0状态在5万步收敛;②收敛马赫数。计算收敛后,初值Ma=0.0状态得到的前方监测点马赫数约为0.94,而初值Ma=0.0状态约为0.93;③收敛过程。初值Ma=0.0状态监测点马赫数单调增加到0.9附近,而初值Ma=0.9状态先增大到1.53后减小到0.90附近,且出现明显超声速气流。
4.3 槽道扩张角
对比状态:槽壁扩张角分别为0.0°和0.3°,其他条件均相同,即再入调节片偏角0°,上下槽壁,出口背压相同,计算步数均为39万步。
槽壁两种扩张角状态下,对称面及Slot 2槽道截面马赫数云图、X站位马赫数云图以及Slot 2槽道流动细节对比情况分别如图14~图16所示。从图14可以看出:两种扩张角得到的流场结构基本相同,其中扩张角0.3°状态得到的马赫数较扩张角0.0°略高。从图15可以看出:两种扩张角得到的流场结构存在一定差异,主要在槽道附近气流速度上,扩张角0.3°状态中槽道低速气流进入试验段,而扩张角0.0°状态则是试验段高速气流进入槽道。从图16可以看出:当槽壁扩张角为0.0°时,气流从试验段和驻室流入槽道内,然后经过再入调节片流回二喉道或驻室,而当槽壁扩张角为0.3°时,气流从驻室流向槽道和试验段,然后再流回槽道内,最后经过再入调节片流回二喉道或驻室。这可能是因为槽壁扩张角0.0°状态下,槽壁未扩张引起试验段截面尺寸不变,而附面层逐渐增厚,气流实际通道面积减小,压力增加,将试验段气流“顶进”槽道。

(a) 扩张角0.0°
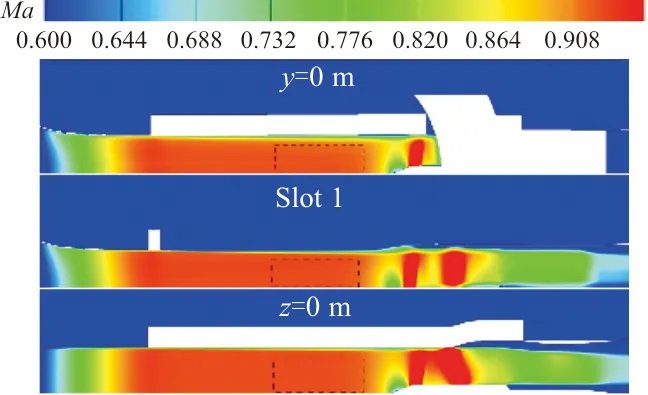
(b) 扩张角0.3°

(a) 扩张角0.0°

(b) 扩张角0.3°

(a) 扩张角0.0°

(b) 扩张角0.3°
不同槽壁扩张角状态下两个监测点马赫数收敛曲线以及试验段轴向马赫数分布情况如图17所示,可以看出:两种槽壁扩张角状态下,前后两点马赫数均在5万步接近收敛,从5万步到39万步变化较小。同时,槽壁扩张角0.3°得到的两点马赫数均较槽壁扩张角0.0°略大,这与图14和图15中各站位马赫数分布结论一致。从图17(a)和(b)可以看出:槽壁扩张角0.0°状态下前后两点马赫数差量保持在0.018 5附近,而槽壁扩张角0.3°状态下则保持在0.008 5附近,两者马赫数差量相差0.01,因此槽壁扩张角0.3°较槽壁扩张角0.0°更能获到均匀的试验段流场。图17(a)中槽壁扩张角0.3°状态中,模型区中心线前后两点马赫数差量抖动较为强烈。从图17(c)可以看出:槽壁扩张角0.3°状态下的试验段马赫数较槽壁扩张角0.0°大,且在模型区域内马赫数分布更加平缓,特别是在接近尾撑附近,槽壁扩张角0.3°得到的马赫数较槽壁扩张角0.0°受尾撑干扰更小。

(a) 扩张角0.0°

(b) 扩张角0.3°
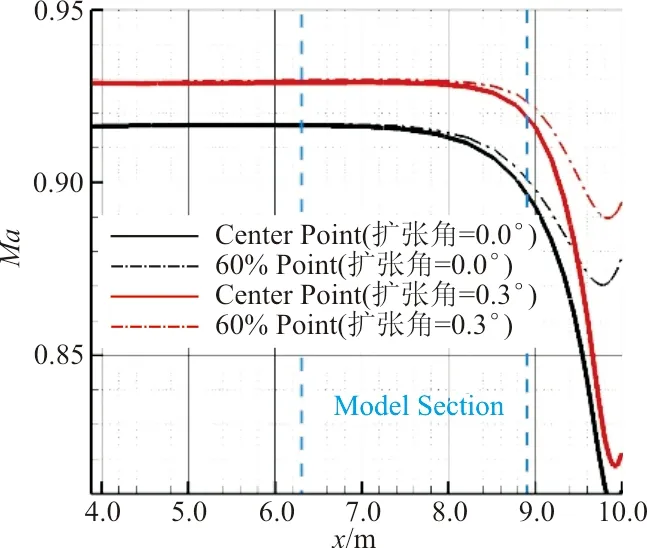
(c) 试验段轴向马赫数分布
通过对比分析,得到两种槽壁扩张角对结果影响明显,特别是试验段轴向马赫数分布上,槽壁扩张角0.3°得到的模型区马赫数差量为0.008 5附近,而槽壁扩张角0.0°状态到达0.018 5,即槽壁扩张角0.3°状态得到的试验段模型区域流场品质更高,且同样条件下得到的试验段马赫更大。风洞高速段槽道处马赫数云图如图18所示,可以看出:气流经稳定段到收缩段喷管速度逐渐增加,在试验段区域保持在跨声速附近,且试验段对称面马赫数分布均匀。

图18 槽壁扩张角0.3°槽道马赫数云图
5 结 论
(1) 采用模型区前后两个监测点马赫数变化以及两者马赫数差量变化作为数值计算收敛评判依据,方法可行且能得到较稳定的模型区流场。
(2) 不同计算初始化条件对收敛结果总体影响较小(试验段马赫数存在一定差异),特别是各截面流场分布和槽道流动方向上,两者结果基本相同。
(3) 在跨声速状态适当增加槽壁扩张角,可提高试验段模型区域流场品质。
(4) 槽道内气流流动方向受槽壁扩张角影响明显,且与试验段和驻室压力关系密切。
由于管道流动较外流复杂,且跨声速风洞高速段一体化数值模拟可参考的研究工作较少,特别是试验段槽壁流动情况,关于试验段槽道附近流动等工作还需深入分析。
